Empresas Ganadoras en un Ambiente Competitivo
Esta es la versión en Español del sitio Web principal en Inglés, el cual se encuentra disponible en:
Introduction to Game Theory
Este sitio web presenta la teoría de un juego Suma- Cero de Dos- Personas con un ejemplo numérico ilustrativo. Incluye también las aplicaciones para una selección de portafolios óptima en una decisión de inversión en conjunto con la evaluación de su riesgo asociado. La teoría de juegos es sin duda un modelo para empresas ganadoras o exitosas en un ambiente competitivo.
Para encontrar este sitio, Intente Editar | Econtrar en la página [Ctrl + f]. Introduzca una palabra o frase en el espacio de diálogo, por ejemplo "riesgo " ó "utilidad " Si la palabra/ frase encontrada no es la que usted buscaba, intente con Próxima busqueda.
MENU
- Introducción y Sumario
- Un Problema de Inversión: Selección Optima de Portafolio
- Una Clasificación de Actitudes Relativas de los Inversionistas con Respecto al Riesgo y su Impacto
- Evaluación de Riesgo: ¿Que Tan Bueno Es Su Portafolio?
- Factores Prioritarios en los Portafolios y Análisis de Estabilidad
- La Probabilidad de Ruina de los Jugadores
- Otras Técnicas de Modelaje de Competencia
Introducción y Sumario
La teoría de juegos describe las situaciones envueltas en conflictos en los cuales el beneficio es afectado por las acciones y contra-reacciones de oponentes inteligentes. El juego suma-cero de dos- personas juega un papel fundamental en el desarrollo de la teoría de juegos.
La teoría de juegos es sin duda un modelo para empresas ganadoras o exitosas en un ambiente competitivo: Por ejemplo, existen muchos factores importantes a considerar cuando se hace una oferta importante, entre los cuales están: Establecer y mantener una posición de preferencia como oferente, desarrollar una relación de preferencia por parte de los clientes, de lo que se oferta en sí mismo, y del precio.
Para desarrollar los conceptos de la teoría de juegos, considere el siguiente juego, en el cual el jugador I tiene dos opciones para escoger, y el jugador II tiene tres alternativas para cada elección del jugador I. La matriz de beneficios T se muestra a continuación:
| Jugador II | ||||
| j=1 | j=2 | j=3 | ||
| Jugador I | i=1 | 4 | 1 | 3 |
| i=2 | 2 | 3 | 4 | |
| ______________________________________ | ||||
| La Matriz de Beneficios | ||||
En la matriz de beneficios, las dos filas (i = 1, 2) representan las dos estrategias posibles que el jugador I puede emplear, y las tres columnas (j = 1, 2, 3) representan las dos estrategias posibles que el jugador II puede emplear. La matriz de beneficios esta orientada al jugador I, lo que significa que un valor positivo tij es ganancia para el jugador I y una pérdida para el jugador II, mientras que un tij negativo representa ganancia para el jugador II y una pérdida para el jugador I. Por ejemplo, si el jugador I utiliza la estrategia 2 mientras que el jugador II aplica la estrategia 1, el jugador I recibe t21 = 2 unidades y por lo tanto el jugador II pierde 2 unidades. Obviamente, en nuestro ejemplo el jugador II siempre pierde; sin embargo, el objetivo es minimizar el beneficio del jugador I.
La representación grafica de los juegos podría ser observada como un Torneo que es jugado en una red de conexiones con direcciones. Bajo este esquema, existen dos tipos de nodos: terminales y continuos. Los nodos terminales no llevan a otros nodos, y el jugador I recibe el beneficio asociado a sus propios arcos. Los nodos continuos llevan a por lo menos un nodo adicional. Ambos jugadores seleccionas simultáneamente un nodo respectivo. Para este ejemplo numérico, a continuación se muestra el gráfico correspondiente. En esta red de conexión con direcciones los bordes van desde el vértice u hasta en vértice w, y si algún jugador elige el u mientras el otro elige el w, este último se encuentra en la cabeza del arco conectando dos nodos, por lo tanto recibe en beneficio tuw.
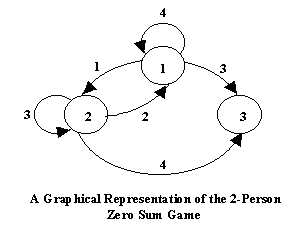
Un "punto de decisión de equilibrio", es decir, un "punto de silla", es también conocido como un "punto mini-máximo", el cual representa una decisión para dos jugadores en la cual ninguno de los dos puede mejorar partiendo unilateralmente de ese punto.
Cuando no existe un punto de silla, se debe elegir una estrategia aleatoria. Esta es la idea detrás de una estrategia mixta. Una estrategia mixta para un jugador esta definida como la distribución de probabilidad sobre el conjunto de todas las estrategias. Nuestro ejemplo numérico es uno de estos casos. El jugador I puede asegurar que el beneficio será maxi minj tij = 2, mientras que el jugador II ajusta su juego suponiendo que el jugador I no recibe mas que min max tij = 3. El problema de cómo la diferencia [minj maxi tij] - [max min tij] ³ 0 debería ser subdividida entre los jugadores se mantiene abierta. En tal caso, los jugadores buscan naturalmente estrategias adicionales de oportunidades para asegurarse ellos mismos que las posibilidades de compartir esta diferencia. Para alcanzar este objetivo, ellos deben seleccionar sus estrategias de manera aleatoria para confundirse el uno al otro
Usaremos un método general basado en la formulación de la programación lineal (PL). Esta equivalencia entre la teoría de juegos y la programación lineal podría ser sorprendente debido a que los problemas de PL envuelven solo un tomador de decisiones, pero se debe notar que con cada problema de PL, existe un problema asociado al mismo llamado problema dual de PL. Los valores óptimos de las funciones objetivo de ambos problemas PL son iguales, correspondientes al valor del juego. Cuando se soluciona la PL mediante el método simple, la solución al problema dual también aparece como parte de la tabla final. De esta forma obtenemos v, Y*, y X* resolviendo una PL. La formulación de la PL y el método simple es el método mas rápido, práctico, y útil para resolver juegos con una matriz T grande. Suponga que el jugador II adopta una estrategia mixta, pero el jugador I solo se le permite utilizar una estrategia pura. ¿Cuál sería la estrategia mixta Y= (y1, y2, y3) que el jugador II debería adoptar para minimizar el beneficio máximo esperado v? Un momento de análisis muestra que el jugador II debería resolver el siguiente problema:
La minimización se encuentra sobre todos los del vector de decisión Y ³ 0, el escalar y no esta restringido en signo, y U un vector columna n-dimensional con todos sus elementos iguales a 1. El lado derecho de las primeras n restricciones, por definición, es el retorno esperado del jugador II en contra de la estrategia pura del jugador I. Estas estrategias mixtas serían óptimas si permitimos que el jugador I emplee estrategias mixtas. Las estrategias mixtas son conocidas también como estrategias de “punto de silla”. Por supuesto, un juego con un punto de silla también puede ser resuelto por este método. La formulación estándar en el método simple requiere que todas las variables sean no-negativas. Para lograr esta condición se debe sustituir la diferencia de dos variables nuevas por y.
La estrategia óptima para el jugador I es la solución del problema dual del jugador II. El método simplex de la programación lineal proporciona estrategias óptimas para ambos jugadores.
Los juegos sociales y las normas de imparcialidad son convenciones que se han desarrollado para coordinar el comportamiento de manera equilibrada del juego de la sociedad llamado vida. Dado este punto de vista, las aproximaciones naturalistas del metafísico Emmanuel Kant y moralista de David Hume podrían ser abandonadas.
Ejemplos Numéricos
La programación lineal para el problema del jugador II en un juego con una matriz de beneficios T dada anteriormente, es:
Min v
sujeta a:
La solución óptima para el jugador II es: y1 = 1/2, y2 = 1/2, y3 = 0. Los precios sombra son las estrategiasóptimas para el jugador I. Por lo tanto, el punto de silla mixto es: x1 = 1/4, x2 = 3/4; y1 = 1/2, y2 = 1/2, y3 = 0, y el valor del juego es igual a 5/2. Note que la estrategia esencial para el jugador I son: i = 1, i = 2; para el jugador II son j = 1, j = 2 mientras j = 3 no es esencial.
Es costumbre el descartar las filas o las columnas dominantes para encontrar las estrategias óptimas. Sin embargo, esto asume que la matriz de beneficios es fija.
En el análisis de decisión, el tomador de decisiones tiene que seleccionar por lo menos y como mucho una opción de todas las alternativas posibles. Esto ciertamente limita su alcance y su aplicación. Usted ha aprendido tanto el análisis de decisión como la programación lineal. Ahora es el momento para utilizar los conceptos de la teoría de juego para conectar estos dos aparentemente diferentes modelos para ampliar y alcanzar modelos de toma de decisiones mas realistas. El problema de inversión puede ser formulado como si el inversor esta jugando en contra de la naturaleza.
Suponga que nuestro inversionista tiene $100,000 para colocarlos en tres inversiones posibles con valores desconocidos Y1, Y2, Y3, respectivamente. Es decir,
Y1 + Y2 + Y3 = 100,000
Note que esta condición es equivalente a la condición de probabilidad total del jugador I en la Teoría de Juegos.
Bajo estos supuestos, los retornos son:
El objetivo es que nuestro rendimiento (retorno) mas bajo (v) sea los mas grande posible.
Formulando este problema de Análisis de Decisión como un problema de Programación Lineal obtenemos:
Max v
sujeta a:
Esta formulación de programación lineal es similar al problema discutido en la sección de Teoría de Juego. De hecho, la interpretación de este problema es que, en esta situación, el inversionista esta jugando en contra de la naturaleza (los estados de la economía.)
Resolviendo este problema por cualquier solución algorítmica de programación lineal, la solución óptima es Y1 = 0, Y2 = 0, Y3 = 100.000, y v = $7000. Esto significa que el inversionista debería colocar todo el dinero en el mercado de depósitos con unretorno acumulado de 100.000´1,07 = $107.000.
Note que la matriz de beneficios para este problema tiene un punto de silla; por lo tanto, como se esperaba, la soluciónóptima es una estrategia pura. En otras palabras, debemos invertir todo nuestro dinero en un solo portafolio.
Como otro ejemplo numérico, considere las dos inversiones siguientes con las tasas de retorno dadas. Dado que usted desea invertir $12,000 en un periodo de un año, ¿Cómo invertiría para la estrategia óptima?
Al igual que el ejemplo anterior, formulando este problema como uno de programación lineal, obtenemos una solución óptima, la cual es una estrategia mixta: Comprar $4000 en divisas extranjeras y $8000 en oro.
El Problema de Inversión Bajo Riesgo: Suponga que la probabilidad subjetiva para cada uno de los estados de la economía estimados son: G(0,4), MG(0,2), NC(0,3) L(0,1). ¿Cómo se debería invertir de forma de maximizar los retornos esperados?
La siguiente tabla muestra las mediciones de riesgo calculadas para el Problema de Decisión de Inversión:
De las columnas de Evaluación del Riesgo en la tabla se llega a la conclusión de que los Bonos son mucho menos riesgosos que las Acciones. Es claro que el Depósito está exento de riesgo. Ahora, la última pregunta es: Con toda la información relevante, ¿qué curso de acción asumir? Todo depende de usted.
Max [v - 0,0322Y1 - 0,0627Y2 -0Y3]
sujeta a:
Esta formulación de programación lineal es similar al problema discutido en la sección de Teoría de Juego. De hecho, la interpretación de este problema es que, en esta situación, el inversionista esta jugando en contra de la naturaleza (los estados de la economía.)
Resolviendo este problema por cualquier solución algorítmica de programación lineal, la solución óptima es Y1 = 0, Y2 = 0, Y3 = 100.000, y v = $7000. Esto significa que el inversionista debería colocar todo el dinero en el mercado de depósitos con unretorno acumulado de 100.000´1,07 = $107.000.
Note que la función objetivo anterior incluye la desviación estándar para reducir el riesgo de su decisión. Sin embargo, es mas apropiado utilizar la matriz de covarianza. La función objetivo tendrá una forma cuadrática, la cual puede ser resuelta aplicando algoritmos de optimización no-lineal. Para obtener mas información sobre la elaboración de problemas, y soluciones de algoritmos, junto a algunos ejemplos numéricos ilustrativos, visite el sitio web de Decisiones Optimas de Negocios.
Usted podría utilizar:
Proceso de Evaluación de Riesgo: Claramente, diferentes modelos de probabilidad subjetiva son estimables que pueden arrojar diferentes resultados. Estos ejemplos muestran que tan importante es estar claro acerca de los objetivos del modelo. Una aplicación importante de los modelos de probabilidad subjetiva es que modelan el efecto de incertidumbre del estado del conocimiento en modelos consecuentes. Normalmente se obtiene que la dependencia entre factores desconocidos puede ser importante en la conducción de los resultados del modelo. Por ejemplo, considere dos portafolios que tienen retornos aleatorias R1 y R2; la relación:
Min v = y
sujeto a:
T.Y £ y
Ut.Y = 1
4y1
+
y2
+
3y3
£
v
2y1
+
3y2
+
4y3
£
v
y1
+
y2
+
y3
=
1
yj³0, j = 1, 2, 3, v es no restringida
Considere el siguiente problema de inversión discutido el sitio web Análisis de Decisión. El problema es decidir que acción o combinación de ellas se debe tomar dentro de tres cursos posibles con las tasas de retorno dadas como sigue en la siguiente tabla.
Estados de la Naturaleza (Eventos)
Crecimiento (G)
G Medio
No Cambios
G Bajo
G
MG
N
L
Acciones
Bonos
12%
8
6
3
Acciones
15
7
3
-2
Depósitos
7
7
7
7
0,12Y1
+
0,15Y2
+
0,07Y3
{Si hay Crecimiento (G)}
0,08Y1
+
0,07Y2
+
0,07Y3
{Si existe un G Medio}
0,06Y1
+
0,03Y2
+
0,07Y3
{Si no Ocurren Cambios}
0,03Y1
-
0,02Y2
+
0,07Y3
{Si el crecimiento es Bajo}
y Y1, Y2, Y3 ³ 0, mientras que v es no restringido en signo (podría tener retornos negativos).
Y1
+
Y2
+
Y3
=
100000
0,12Y1
+
0,15Y2
+
0,07 Y3
³
v
0,08Y1
+
0,07Y2
+
0,07Y3
³
v
0,06Y1
+
0,03Y2
+
0,07Y3
³
v
0,03Y1
-
0,02Y2
+
0,07Y3
³
v
Estados de la Naturaleza (Eventos)
Crecimiento (G)
G Medio
No Cambios
G Bajo
G
MG
N
L
Acciones
Divisas
5
4
3
-1
Oro
2
3
4
5
Evaluación del
riesgo
C (0,4)
CM (0,2)
SC (0,3)
B (0,1)
Valor esperado
Desviación estándar
C. V.
Bonos
12
8
6
3
8,5
3,12
37%
Acciones
15
7
3
-2
8,1
6,11
75%
Depósito
7
7
7
7
7
0
0%
y Y1, Y2, Y3 ³ 0, mientras que v es no restringido en signo (podría tener retornos negativos).
Y1
+
Y2
+
Y3
=
100000
0.12Y1
+
0.15Y2
+
0.07 Y3
³
v
0.08Y1
+
0.07Y2
+
0.07Y3
³
v
0.06Y1
+
0.03Y2
+
0.07Y3
³
v
0.03Y1
-
0.02Y2
+
0.07Y3
³
v
la Teoría de Juegos Suma –Cero de Dos- Personas con Aplicaciones para comprobar sus cálculos y experimentaciones.
El siguiente diagrama de flujo explica el proceso de evaluación de riesgo para la selección de portafolios basados en sus series de tiempo financieras.
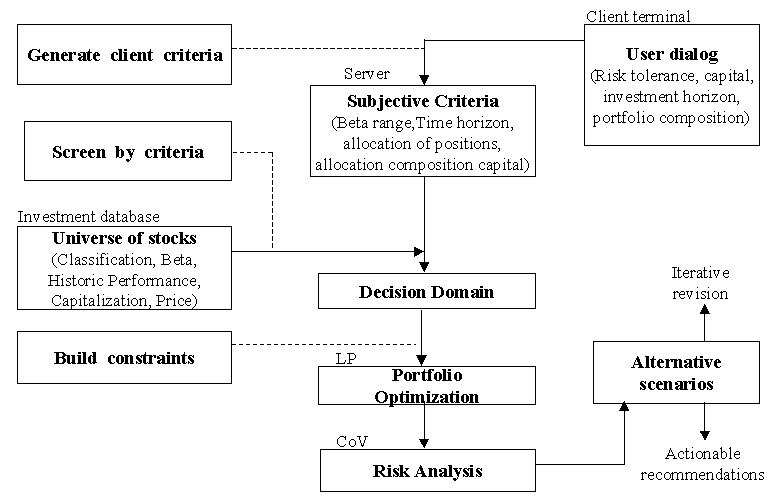
Evaluación de Riesgo en la Selección de Portafolios
haga click en la imagen para agrandarla
El modelo híbrido anterior trae las técnicas del análisis de decisión, programación lineal, y evaluación estadística de riesgo (mediante la función cuadrática de riesgo definida por la matriz de covarianza) para soportar las decisiones iterativas para el modelo de alternativas de inversión.
Una Clasificación de Actitudes de los Inversionistas en Relación al Riesgo y su Impacto
Probabilidad de un Evento y el Impacto de su Ocurrencia: La aproximación del proceso-orientado de gerenciar el riesgo e incertidumbre es parte del modelaje probabilístico. Esto permite al tomador de decisiones examinar el riesgo dentro de sus retornos esperados, e identificar los asuntos críticos de evaluar, limitar, y mitigar el riesgo. Este proceso envuelve tanto aspectos cuantitativos como cualitativos de la evaluación del impacto del riesgo.La ciencia de la decisión no describe lo que las personas hacen dado que existen tanto problemas para calcular la probabilidad y la utilidad de los resultados. Las decisiones también pueden afectadas por la racionalidad subjetiva de las personas y por la manera que el problema de decisión sea percibido.
Tradicionalmente, el valor esperado de una variable aleatoria ha sido utilizado como la mayor ayuda para cuantificar el monto de riesgo. Sin embargo, el valor esperado no es necesariamente una buena medida por si solo para tomar decisiones, dado que distorsiona la distinción entre probabilidad y severidad. Para demostrarlo, considere el ejemplo siguiente:
Suponga que una persona debe tomar una decisión entre los escenarios 1 y 2 a continuacón:
- Escenario 1: Existe 50% de chance de perder $50, y a 50% de chance de no perderlo.
- Escenario 2: Existe 1% de chance de perder $2500, y un 99% de chance no perderlo.
Ambos escenarios resultan en una pérdida esperada de $25, pero esto o refleja el hecho de que el escenario 2 es mucho mas riesgoso que el primero. (Por supuesto que esto es una evaluación subjetiva). El tomador de decisiones podría estar mas preocupado acerca de minimizar el efecto de ocurrencia de un evento extremo del cual el o ella se encuentra preocupado por la media. La tabla siguiente explica la complejidad de la probabilidad de un evento, el impacto de ocurrencia de un evento y si indicador de riesgo asociado respectivamente:
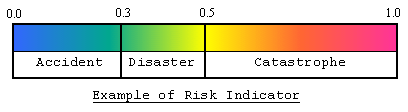
De la sección anterior, se puede recordar que la certidumbre equivalente el beneficio libre de riesgo; adicionalmente, la diferencia entre la certidumbre equivalente del tomador de decisiones y el valor monetario esperado (VME) es llamada la prima de riesgo. Podríamos utilizar el signo y la magnitud de la prima de riesgo para clasificar la actitud relativa del tomador de decisiones en relación con el riesgo de la manera siguiente:
- Si la prima de riesgo es positiva, el tomador de decisiones esta deseando tomar el riesgo, por lo tanto se le llama buscador de riesgo. Claramente, algunas personas son mas buscadores de riesgo que otras.
- Si la prima de riesgo es negativa, el tomador de decisiones evitará el riesgo, por lo tanto se le llama adverso al riesgo.
- Si la prima de riesgo es cero, el tomador de decisiones se le llama riesgo neutral.
¿Evaluación de Riesgo: Que Tan Bueno es Su Portafolio?
El riesgo es la adversidad de las apuestas, el cual se describe en términos de probabilidad. La evaluación de riesgo es un procedimiento para cuantificar los valores de pérdida o de la ganancia y proporcionarles con los valores propios de probabilidad. En otras palabras, la evaluación de riesgo significa construir la variable aleatoria que describe el riesgo. El indicador de riesgo es una cantidad describe la calidad de la decisión.Si la perdida de la generalidad, considere nuestro ejemplo de inversión anterior. Suponga que el portafolio óptimo es:
El valor esperado (es decir, el average): El retorno esperado es:
donde, Br, Sr, y Dr son los averages históricos de B, S, y D, respectivamente.
El retorno esperado por si solo no es un buen indicador de la calidad de la decisión. La varianza necesita ser conocida de forma tal que se pueda tomar una decisión educada. ¿Alguna vez ha escuchado el dilema del estadístico de 2 metros de alto que se ahogó en un río de un 1,5 metros de average de profundidad?
En el ejemplo de la inversión, también es necesario calcular el riesgo asociado al portafolio óptimo. Una medida de riesgo es generalmente reportada por variación, o su raíz cuadrada llamada desviación estándar. La variación y desviación estándar son valores numéricos que indican la variabilidad inherente a su decisión. Para el riesgo, valores mas pequeños indican que lo que se esperaba podría ser lo que se obtendría. Lo que deseamos es un retorno esperado grande, con riesgo pequeño; por lo tanto, alto riesgo hace que el inversionista se preocupe.
Varianza: An important measure of risk is variance:
2Y1.Y2.Cov(B, S) + 2Y1.Y3.Cov(B, D) + 2Y2.Y3.Cov(S, D)
De donde Var y Cov son la varianza y covarianza, respectivamente, estas son calculadas utilizando datos recientes.
La varianza es una medida de riesgo; pro lo tanto, mientras masa grande sea la varianza, mas grande es el riesgo. La varianza no se expresa en los mismos términos del valor esperado. Por lo tanto, es difícil de entender y de explicar como resultado del término al cuadrado cuando se calcula. Esto puede ser aliviado cuando se trabaja con la raíz cuadrada de la varianza, el cual es llamada la Desviación Estándar:
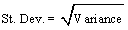
Tanto la varianza como la desviación estándar proporcionan la misma información; por lo tanto, la una se puede obtener directamente de la otra. En otras palabras, el proceso de calcular la desviación estándar envuelve el cálculo de la varianza. Dado que la desviación estándar es la raíz cuadrada de la varianza, se expresa en las mismas unidades que el valor esperado.
Para el proceso de decisión dinámico, la Volatilidad como medida de riesgo incluye el período de tiempo sobre el cual la desviación estándar es calculada. La medida de Volatilidad esta definida como la desviación estándar dividida por la raíz cuadrada de la duración del tiempo.
Cuando se consideran dos portafolios diferentes, ¿Qué haría si un portafolio tiene un retorno esperado mayor, pero con un riesgo mucho mayor que el portafolio alternativo? In tal caso, utilice otra medida de riesgo conocida como el Coeficiente de Variación.
Coeficiente de Variación (CV) es la desviación relativa absoluta con respecto al tamaño 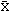 provisto que
provisto que 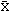 es no cero, expresado en porcentaje:
es no cero, expresado en porcentaje:
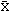 | %
| %
Note que el CV es independiente de la medida del valor esperado. El coeficiente de variación demuestra la relación entre la desviación estándar y el valor esperado, mediante la expresión del riesgo como porcentaje del valor esperado. Un portafolio con 10% o menos de CV es considerado “bueno”. La inversa del CV (1/CV) se llama ratio de Señal de Ruido.
La Diversificación podría reducir su riesgo: Dado que la covarianza aparece en la evaluación del riesgo, este reduce el riesgo si es negativo. Por lo tanto, diversificando su inversión podría reducir el riesgo sin reducir los beneficios recibidos por sus actividades. Por ejemplo, usted podría escoger el comprar una variaedad de acciones diferentes en vez de una sola.
A usted podría gustarle utilizar el siguiente JavaScript para propósitos de cálculos y de experimentos computacionales como herramientas para el análisis de riesgo fundamental:
- Estadísticos Computacionales para Distribuciones Multinomiales
- Media, Desviación Estándar y Coeficiente de Variación
- Estadísticos de MultiVariación: Media, Varianza y Covarianza
Factores de Prioridad de Portafolios y Análisis de Estabilidad
Introducción: El análisis de sensibilidad, conocido también como análisis de estabilidad, es una técnica utilizada para determinar en que medida un retorno esperado cambiará en respuesta a cambio dado en las variables de entrada, dado que las otras variables permanecen constantes.Pasos en el Análisis de Sensibilidad:
- Comience con la consideración de un caso-base en una situación nominal, usando los valores esperados para cada valor de entrada.
- Calcule los resultados del caso-base.
- Considere una serie de preguntas “que pasa si” para determinar en cuanto los resultados se derivarán del nivel nominal si los valores de entrada son derivados de sus valores esperados.
- cada valor de entrada es cambiado por varios puntos porcentuales por debajo y por arriba de su valor esperado, y el beneficio esperado es calculado.
- El conjunto de beneficios esperados son sustituidos en contra de la variable que fue cambiada.
- Mientras más inclinada sea la pendiente (derivada) de la línea resultante, más sensible será el cambio en las variables en referencia al valor esperado del beneficio.
Análisis de Escenarios: El análisis de escenarios es una técnica de análisis de riesgo que considera tanto la sensibilidad del beneficio esperado en las variables claves como también el rango del valor de las variables. El peor y mejor conjunto de circunstancias “razonables” son consideradas, y el beneficio esperado para cada uno es calculado y comparado al esperado, o caso-base, output. Claramente, escenarios extensivos y análisis de sensibilidad pueden ser llevados a cabo utilizando versiones computarizadas del procedimiento anterior.
¿Qué tan Estable es su Decisión? El análisis de estabilidad compara los resultados de cada escenario con los chances de eventos. Versiones computarizadas del procedimiento anterior son necesarias y herramientas útiles. Estas pueden ser utilizadas extensamente para examinar las decisiones para estabilidad y sensitividad siempre que exista incertidumbre en la tasa de retorno.
Prioridad de los Factores Incontrolables: El análisis de estabilidad también proporciona modelos críticos de variables de entrada. La prueba de sensibilidad mas simple es si un portafolio óptimo cambia cuando el factor de incertidumbre es fijado a un valor extremo mientras que las otras variables permanecen constantes. Si la decisión no cambia, la incertidumbre puede ser dejada como un factor de menor importancia con respecto a los demás. El análisis de sensibilidad se enfoca en los factores con mayor impacto, por lo tanto ayudando a darle prioridad a la recolección de datos mientras incrementa la confiabilidad en la información.
A usted podría gustarle utilizar el JavaScript de Estadísticos de MultiVariación: Media, Varianza, y Covarianza para comprobar sus cálculos y para realizar experimentos asistidos por computadoras.
La Probabilidad de Ruina del Apostador
Para este momento, usted debería haberse dado cuenta que el juego anterior no es un problema de puras decisiones aleatorias. Cambiando a estrategias diferentes con frecuencias específicas obtenidas por soluciones óptimas es el objetivo de confundir a otros jugadores. El siguiente juego es un ejemplo de un problema de toma de decisión aleatoria pura.Probabilidad de Ruina: El segundo JavaScript es para el análisis de sensibilidad de ganar el total del premio en dólares o perderlo todo (ruina.)
Dejemos que R = la cantidad de dinero que se apuesta, T = el objetivo en monto de dólares, U = el tamaño de cada apuesta, y p = la probabilidad de ganar alguna apuesta, luego la probabilidad de la probabilidad (W) de alcanzar el objetivo, es decir, irse con $(R+T ) es:
y
Por lo tanto, la probabilidad de ruina, es decir, la probabilidad de perder todo $R es: (1 – W).
Note: Estos resultados están sujetos a la condición de que el monto objetivo ($T) debe ser mucho menor que el dinero que se trajo a apostar ($R). Es decir ($T) debe ser una fracción (f) de ($R).
Recuerde que si se apuesta demasiado usted se irá como un perdedor, mientras que si usted apuesta poco, su capital se incrementará lentamente. Usted se preguntará que fracción (f) de R se deberá apostar siempre. Deje que V sea el monto que usted gana por cada dólar que arriesga, luego la fracción óptima es:
A usted podría gustarle utilizar el JavaScript de El Juego del Apostador Suma-Cero de Dos- Personas y sus Aplicaciones para comprobar sus resultados y para realizar experimentaciones numéricas asistidas por computadoras.
Otras Técnicas de Modelos de Competencia
La competencia en los negocios siempre ocurre dado los efectos negativos de alguna de las partes sobre otra ( es decir, compañía), dada la reducción de los recursos escasos compartidos. La competencia es un mecanismo que llega al crecimiento logístico. El modelo de crecimiento logístico es expresado como:
r = tasa de crecimiento de per-capita de la población,
K = transportando la capacidad del ambiente,
La pregunta principal es la siguiente. ¿Podría el factor de capacidad de transporte en la ecuación logística ser una función en vez de ser una constante? La competencia de dos tecnologías, por ejemplo, wireless versus cable o templadura simulada versus un algoritmo genético puede ser intrigante. Aquí, las dos partes son simplemente competidores, uno se “come” al otro --, así como cuando el consumidor es la verdadera "presa" aunque a veces complaciente. El modelo de Lotka-Voterra y sus múltiples variantes son métodos ampliamente usados en muchas disciplinas, incluyendo la economía.
El modelo clásico de competencia de Lotka-Volterra es descrito por el siguiente sistema de ecuaciones diferenciales:
dN2 / dt = r2 N2 (K2 - N2 - bN1)/K2
Cualquier extensión para la modificación del modelo de competencia de Lotka-Volterra debe solucionar las debilidades siguientes: El modelo asume que la presa crece espontáneamente y que su capacidad de transporte del ambiente no tiene límite. Adicionalmente, removiendo el supuesto de que todos los predadores y las presas comienzan en el mismo punto espacial produce un conjunto de resultados interesantes, útiles, y mas realistas.
Declaración de derechos de propiedad intelectual: El uso legítimo, según las pautas de 1994 guías de consulta
justas del uso para los multimedia educativos, de los materiales presentados en este sitio Web está permitido para propósitos educativos no comerciales.
Este sitio puede duplicarse,
intacto con esta declaración, en cualquier servidor de acceso público y puede vincularse a cualquier otra página Web. Todos los archivos se encuentran disponibles en
http://home.ubalt.edu/ntsbarsh/Business-stat para el duplicado.
Agradecería recibir comentarios, sugerencias e inquietudes por e-mail. Gracias.