Optimización de Enteros y Modelos de Redes
Esta es la versión en Español del sitio Web principal en Inglés, el cual se encuentra disponible en:
Integer Optimization and the Network Models
Los programas lineal estándar asumen que las variables de decisión son continuas. Sin embargo, en muchas aplicaciones, los valores de fracciones podrían ser de poco uso así como es mostrado en algunas aplicaciones útiles.
Para buscar el sitio, intente Editar | Encuentre en la página [Ctrl + f]. Entre una palabra o frase en la caja de diálogo, por ejemplo "parámetro " o "lineal " Si la primera aparición de la palabra /frase no es la que estaba buscando, intente Nueva Búsqueda.
MENU
- Introducción a los Modelos de Redes
- Problemas de Transporte
- Problemas de Asignación
- Problema del Camino Mas Corto
- Problemas de Flujo Máximo
- Camino Crítico en la Planificación de Proyectos de Redes
- Problemas de Flujos Costos Mínimos
- Análisis de Sensibilidad para los Modelos de Redes
Programas Lineales Generales de Números Enteros
- Introducción y Sumario
- Aplicaciones de Programas de Integración Mixta: Restricciones "La una- o la otra"
- Relaciones Condicionales Entre Restricciones
- Restricciones de Encendido-Apagado (On- Off)
- Intervalos de Encendido-Apagado On- Off)
- Un Caso de una Variable Discreta Definida Evaluada
- Programas Lineales de Enteros 0 - 1 (Programación Lineal Binaria): El Problema del Morral
- El Problema de Viaje del Vendedor
- Aplicaciones al Presupuesto de Capitales
- Problemas de Horarios
- Aplicaciones al Mercadeo
- El Problema de Recorte de Reservas
- Una Aplicación a la Ingeniería: Mezclando Substancias
Sitios Adjuntos:
- Ciencia de la Administración Aplicada para Gerentes y Lideres Gerenciales
- Modelos Deterministas: Optimización lineal
- Construcción de Regiones de Sensibilidad General de Programación Lineal
- Introducción a la Teoría de Juegos
- Razonamiento Estadístico para la Toma de Decisiones Gerenciales
- Modelos Probabilísticos: Del análisis de la decisión,
Sitio Espejo para España, Sitio Espejo para América Latina. - Toma de Decisiones con Periodos de Tiempo Crítico en Economía y Finanzas
- Una Clasificación de JavaScript Estadíticos
Introducción a los Modelos de Redes
Los modelos de redes son aplicables a una extensa variedad de problemas de decisión, los cuales pueden ser modelados como problemas de optimización de redes que pueden ser eficiente y efectivamente resueltos. Algunos de estos problemas de decisión son realmente problemas físicos, tales como el transporte o flujo de bienes materiales. Sin embargo, muchos problemas de redes son mas que una representación abstracta de procesos o actividades, tales como el camino crítico en las actividades entre las redes de un proyecto gerencial.
La familia de redes de los problemas de optimización incluye los siguientes prototipos de modelos: Problemas de asignación, camino crítico, flujo máximo, camino mas corto, transporte y costo mínimo de flujos. Los problemas son establecidos fácilmente mediante el uso de arcos de redes y de los nodos.
¿Que es un Nodo? Es usualmente llamado vértice, o punto. Es usualmente representado por un circulo. En las redes de transporte, estos deberían ser las localidades o las ciudades en un mapa.
¿Que es un Arco? Es usualmente llamado borde o flecha. Este podría ser directo o indirecto. La cabeza es el destino, y la cola el origen. La cabeza y la cola son nodos que pueden estar tanto al origen como al final. En las redes de transporte, los arcos podrían ser los caminos, los canales de navegación en un río, o los patrones de vuelo de un avión. Los arcos proporcionan la conectividad entre los nodos. Una calle de una sola dirección podría ser representada por un arco, mientras que una calle de dos direcciones podría representada por un arco sin dirección o por dos arcos que apuntan a direcciones opuestas.
Una red con n nodos podría tener tantos arcos como n! /[(n-2)! 2!] = n(n-1)/2. Si están dirigidos, este número pudiese ser doble. Este enorme número de arcos posibles es una de las razones del porque existen soluciones de algoritmos especiales para problemas de redes particulares.
Problemas de Transporte
Los modelos de transporten juegan un papel importante en la gerencia logística y en la cadena de insumos para reducir costos y mejorar servicios. Por lo tanto, el objetivo es encontrar la manera más efectiva en termino de costos para transportar bienes.Un distribuidor que tiene m depósitos con un abastecimiento de productos ai ith en ellos, debe enviar dichos productos a n centros minoristas geográficamente dispersos, cada uno con una demanda de clientes dada ej, la cual debe ser cubierta. El objetivo es determinar el mínimo costo posible de transporte dados los costos por unidad de transportar entre el ith depósito y el jth centro minorista, el cual es Cij.
En el problema siguiente el objetivo es encontrar la forma mas efectiva de transportar los productos. Tanto como la oferta y la demanda en cada fuente se encuentra determinada. Por ejemplo, la fuente (u origen) 3 tiene 800 unidades disponibles mientras que el destino 1 necesita por lo menos 1100 unidades. Cada ruta desde un origen a un destino se le asigna una unidad de costo de transporte.
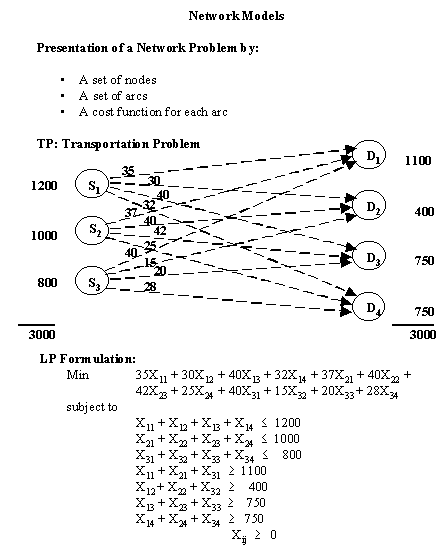
Utilizando el paquete de programación lineal, la solución proporciona la cantidad a ser enviada desde una fuente de origen a un destino. Los resultados son::
Enviar 850 unidades desde la fuente 1 al destino 1
Enviar 350 unidades desde la fuente 1 al destino 2
Enviar 250 unidades desde la fuente 2 al destino 1
Enviar 750 unidades desde la fuente 2 al destino 4
Enviar 50 unidades desde la fuente 3 al destino 2
Enviar 750 unidades desde la fuente 3 al destino 3
El costo total de envío es $84000.
El Problema Dual de Transporte:
El problema dual para el ejemplo numérico anterior es:
Max 1200U1 + 1000U2 + 800U3 + 1100V1 + 400V2 + 750V3 + 750V4
sujeto a:
U1 + V1 £ 35, U1 + V2 £ 30, U1 + V3 £ 40, U1 + V4 £ 32
U2 + V1 £ 37, U2 + V2 £ 40, U2 + V3 £ 42, U2 + V4 £ 25
U3 + V1 £ 40, U3 + V2 £ 15, U3 + V3 £ 20, U3 + V4 £ 28
Ninguna de las Ui y Vj tiene restricción en el signo.
La formulación dual sugiere que intentemos cada envió de bienes de forma tal que la diferencia en los precios unitarios Ui al i-ésimo origen, y el precio por unidad de Vj al j-ésimo destino no exceda el costo de transporte por unidad entre el i-ésimo origen y el j-ésimo destino.
La interpretación de las restricciones duales como el objetivo de que el la diferencia de precios de origen-destino no excede el precio del transporte, es equivalente al principio de equilibrio con un significado económico. Adicionalmente, se puede interpretar el objetivo dual como el propósito de un transportista en maximizar su utilidad cuando compra en un origen y vende en un destino.
Para resolver el problema dual, a usted podría gustarle intentar el Método Algebraico.
Problema de Transportación Discreto: En el problema de transportación discreto toda la oferta de una fuente de origen dada debe ser enviada a solo uno de los destinos disponibles, por lo tanto, es una instancia del Problema de Asignación Generalizado(PAG). El modelo de PAG puede ser formulado como un problema discreto (0-1) generalizado de red con ofertas de en el origen, y multiplicadores conocidos como los factores de ganancia sobre los arcos. Cada arco puede llevar un flujo de solo 0 o 1, pero el monto de flujos transportados a los destinos es igual al numero de multiplicadores de los arcos.
Problema de Asignación
Normalmente, se tienen un grupo n de “concursantes” aplicando para n “empleos”, y el costo no-negativo Cij de asignar el iésimo concursante al jésimo empleo es conocido. El objetivo es asignar un empleo a cada concursante de tal forma de alcanzar el costo total mínimo posible. Defina las variables binarias Xij con un valor de 0 o 1. Cuando Xij = 1, significa que deberíamos asignar al concursante i el empleo j. De lo contrario, (Xij = 0), no deberíamos asignar al concursante i el empleo j.El problema de asignación es un caso especial del problema de transporte, el cual ocurre cuando cada oferta es 1 y cada demanda es 1. En este caso, la integración implica que cada oferente asignará un destino y cada destino tendrá un oferente. Los costos proporcionan las bases para la asignación correspondiente a un oferente y un destino.
Suponga que queremos imponer la condición de que la persona i no debería realizar el trabajo j, o que la persona k no debería realizar el trabajo m. Esto significa que Xij.Xkm = 0. Esta condición no-lineal es equivalente a la restricción lineal Xij + Xkm £ 1. Esta restricción debería ser agregada al conjunto de restricciones como una restricción aparte. Con esta restricción adicional, el problema de asignación se convierte en una programación lineal integral, el cual puede ser resuelto por muchos software tales como LINDO ó QSB.
En el problema siguiente, el objetivo es asignar personas a labores particulares mientras se minimiza el costo total. La función objetivo considera el costo que implica que cada persona realice una actividad en particular. La restricción dice que cada persona debe ser asignada a una actividad, y cada actividad debe ser asignada a solo una persona.
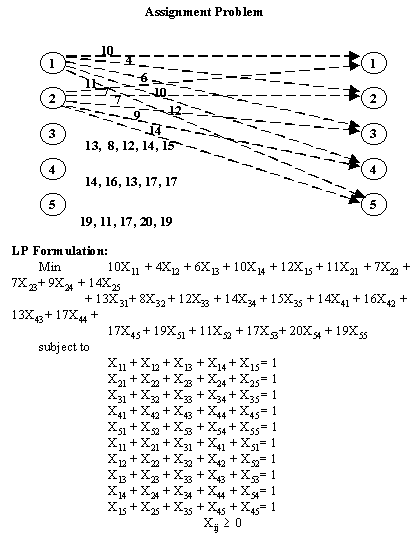
Luego de correr el problema en cualquier paquete que proporcione soluciones de programación lineal, los resultados son:
Persona 1 debería ir al trabajo 3
Persona 2 debería ir al trabajo 4
Persona 3 debería ir al trabajo 5
Persona 4 debería ir al trabajo 1
Persona 5 debería ir al trabajo 2
El costo total es $55.
El Problema Dual de Asignación:
El problema dual para el ejemplo anterior es:
Max U1 + U2 + U3 + U4 + U5 + V1 + V2 + V3 + V4 + V5
sujeto a:
U1 + V1 £ 10, U1 + V2 £ 4, U1 + V3 £ 6, U1 + V4 £ 10, U1 + V5 £ 12
U2 + V1 £ 11, U2 + V2 £ 7, U2 + V3 £ 7, U2 + V4 £ 9, U2 + V5 £ 14
U3 + V1 £ 13, U3 + V2 £ 8, U3 + V3 £ 12, U3 + V4 £ 14, U3 + V5 £ 15,
U4 + V1 £ 14, U4 + V2 £ 16, U4 + V3 £ 13, U4 + V4 £ 17, U4 + V5 £ 17
U5 + V1 £ 19, U5 + V2 £ 11, U5 + V3 £ 17, U5 + V4 £ 20, U5 + V5 £ 19
todas las Ui y Vj son variables libres.
La formulación dual sugiere que intentemos asignar de tal manera que la suma de los valores Ui de la i-ésima persona y el valor agregado Vj de realizar el j-ésimo trabajo, no exceda el costo de asignar la i-ésima persona al trabajo j-ésimo.
Para resolver el problema dual, a usted lo podría gustar probar el Método Algebraico .
También visite los sitio web Software del Problema de Asignación .
El Problema del Camino mas Corto
El problema es determinar la mejor manera de cruzar una red para encontrar la forma mas económica posible desde un origen a un destino dado. Suponga que en una red dada existen m nodos y n arcos (bordes) y un costo Cij asociado con cada arco (i a j) en la red. Formalmente, el problema del camino mas corto (CC) es encontrar el camino mas corto (menor costo) desde el nodo de comienzo 1 hasta el nodo final m. El costo del camino es la suma de los costo de cada arco recorrido. Defina las variables binarias Xij, donde Xij =1 si el arco (i a j)es sobre el CC y Xij = 0 de lo contrario. Existen dos nodos especiales llamados origen y destino. El objetivo es encontrar el camino mas corto entre el origen y el destino.El la red siguiente, varios costos son asignados para el camino que va de un nodo a otro. Por ejemplo, el costo de ir desde el nodo 2 al 4 es 6. La función objetivo considera los costos de moverse de un nodo a otro, o de un origen a un destino. Las restricciones están divididas en tres grupos. La restricción del nodo de origen dice que debe dejar el nodo 1 para ir al 2 o 3. La restricción del nodo intermedio dice que si siempre que se dirija a un nodo usted deberá dejar ese nodo. El nodo de destino es similar al nodo de origen dado que se puede alcanzar este nodo solo desde los nodos vecinos.
Considere la siguiente red dirigida (para una red indirecta, haga que los arcos estén dirigidos en ambas direcciones, luego aplique la misma formulación. Note que en este caso usted tiene Xij y Xji variables). El objetivo es encontrar el camino mas corto desde el nodo 1al nodo 7.
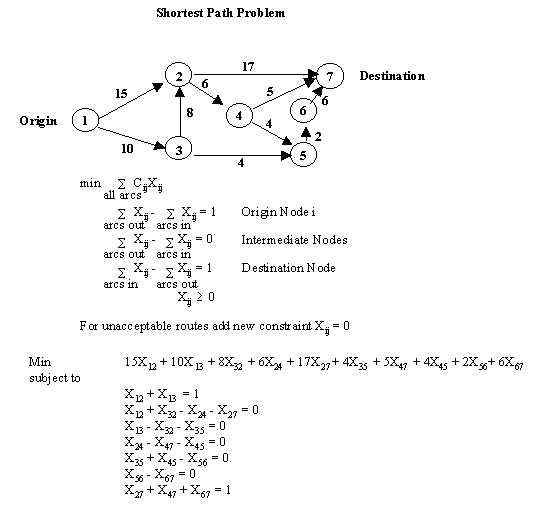
Luego de correr el problema en cualquier paquete que solucione programación lineal, los resultados son:
Ir desde 1 hasta el 3
Ir desde 3 hasta el 5
Ir desde 5 hasta el 6
Ir desde 6 hasta el 7
Este es el camino mas corto con un total de 22 unidades de longitud.
Construya el problema dual para el ejemplo numérico anterior y proporcione una interpretación. Resuelva el problema dual mediante el Método Algebraico.
Note que, los resultados de los paquetes de programación lineal con respecto al análisis de sensibilidad para los problemas de redes podrían ser engañosos. Por lo tanto, para el análisis de sensibilidad del camino mas corto, lea el artículo siguiente:
Arsham H., Análisis de Sensibilidad para el Problema del Camino mas corto, Journal of Congressus Numerantium, Vol. 133, No. 1, 171-210, 1998.
Problema del Flujo Máximo
En una red con flujo de capacidades en los arcos, el problema es determinar el flujo máximo posible proveniente de los orígenes de forma tal de ahogar las capacidades de flujos de los arcos. Considere una red con m nodos y n arcos con un flujo simple de bienes. Denote el arco de flujo (i a j) como Xij. Asociamos cada arco a una capacidad de flujo, kij. En esta red, deseamos encontrar el flujo total máximo en la red, F, del nodo 1 al nodo m.En la formulación de la programación lineal, el objetivo es maximizar F. El monto que parte del origen por varias rutas. Para cada nodo intermedio, lo que entra debe ser igual a lo sale. En algunas rutas los flujos pueden tomar ambas direcciones. La capacidad que puede ser enviada a una dirección en particular también es mostrada en cada ruta.
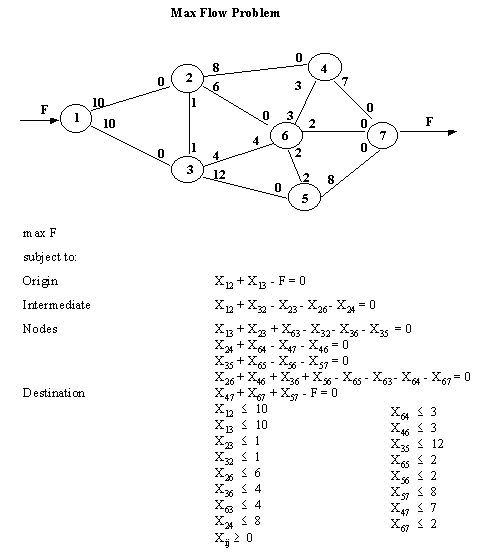
Luego de resolver este problema de PL mediante el uso de LINDO (entre otros software), obtenemos los siguientes resultados:
Enviar 10 unidades de 1 a 2
Enviar 7 unidades de 1 a 3
Enviar 3 unidades de 2 a 6
Enviar 7 unidades de 2 a 4
Enviar 4 unidades de 3 a 6
Enviar 6 unidades de 3 a 5
Enviar 7 unidades de 4 a 7
Enviar 8 unidades de 5 a 7
Enviar 3 unidades de 6 a 3
Enviar 2 unidades de 6 a 5
Enviar 2 unidades de 6 a 7
El flujo máximo es F= 17 unidades.
El Problema Dual de Flujo Máximo:
El problema dual para el ejemplo numérico anterior es:
Min 10Y12 + 10Y13 + Y23 + Y32 + 6Y26 + 4Y36 + 4Y63 + 8Y24
3Y64 + 3Y46 + 12Y35 + 2Y65 + 2Y56 + 8Y75 + 7Y47 + 2Y67
sujeto a:
X2 - X1 + Y12 ³ 0, X3 - X1 + Y13 ³ 0, X3 - X2 + Y23 ³ 0,
X3 - X2 + Y32 ³ 0,
X6 - X2 + Y26 ³ 0,
X6 - X3 + Y36 ³ 0,
X3 - X6 + Y63 ³ 0,
X4 - X2 + Y24 ³ 0,
X4 - X6 + Y64 ³ 0
X6 - X4 + Y46 ³ 0,
X5 - X3 + Y35 ³ 0,
X5 - X6 + Y65 ³ 0,
X6 - X5 + Y56 ³ 0,
X5 - X7 + Y75 ³ 0,
X7 - X4 + Y47 ³ 0,
X7 - X6 + Y67 ³ 0,
X1 - X7 ³1, y
Yij ³ 0, y todos los Xi son variables libres.
La formulación dual sugiere que se intente asignar flujos a arcos de misma manera que para cada arco, la diferencia en valores en el nodo inicial y el nodo final excede el valor agregado.
Para resolver el problema dual, a usted podría gustarle intentar el Método Algebraico .
Adicionalmente visite la página web Problema de Flujo Máximo.
Camino Crítico en la Planificación de Proyectos de Redes
La gerencia exitosa de un proyecto ambicioso, ya sea de construcción, de transporte o financiero, descansan en una coordinación y planificación minuciosa de varias tareas. El Método de Camino (o trayectoria) Crítico (MCC) intenta analizar la planificación de proyectos. Esto posibilita un mejor control y evaluación del proyecto. Por ejemplo, queremos saber ¿Cuanto tiempo durará el proyecto?, ¿Cuándo se estará listo para comenzar una tarea en particular?, si la tarea no es completada a tiempo, ¿El resto del proyecto se retrasará?, ¿Qué tareas deben ser aceleradas (efectivo) de forma tal de terminar el proyecto antes?Dado una red de actividades, el primer problema que nos interesa es determinar la amplitud del tiempo requerido para finalizar el proyecto y el conjunto de actividades que controlan el tiempo para culminar el proyecto. Suponga que en un proyecto de actividades de redes determinado existen m nodos, n arcos (i.e. actividades) una duración de tiempo estimada, Cij, asociada a cada arc (i a j) en la red. El nodo inicial de un arco corresponde al comienzo de la actividad asociada y al nodo final que completa la actividad. Para encontrar el camino o trayectoria crítica (CC), se definen las variables binarias Xij, donde Xij = 1 si la actividad i j es sobre la CC y Xij = 0 por lo contrario. La amplitud de la trayectoria es la suma de la duración de las actividades en la trayectoria. La amplitud de la trayectoria mas larga es el tiempo mas corto que es necesario para completar el proyecto. Formalmente, el problema de CC es encontrar la trayectoria mas larga desde el nodo 1 hasta el nodo m.
Cada arco tiene dos funciones: que representa una actividad y que define la relación presente entre las actividades. Algunas veces es necesario agregar arcos que solo representen relaciones precedentes. Estos arcos ficticios son representados por flechas rotas. En nuestro ejemplo, el arco que va de 2 a 3 representa una actividad ficticia.
La primera restricción dice que el proyecto debe comenzar. Para cada nodo intermedio, si es alcanzado alguna vez, se debe abandonar. Finalmente, la última restricción fuerza la culminación del proyecto.
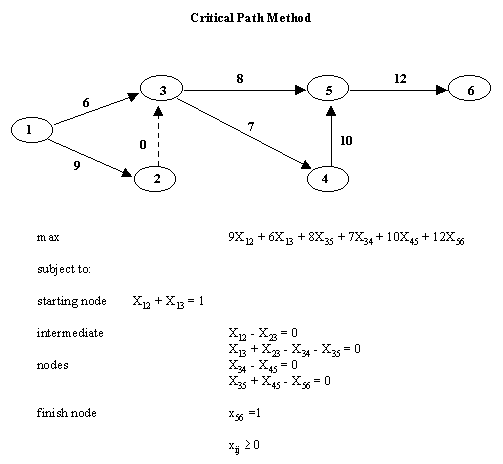
Realizando la corrida del la PL en cualquier software que lo genere, la trayectoria crítica es:
Del nodo 1 al 2
Del nodo 2 al 3
Del nodo 3 al 4
Del nodo 4 al 5
Del nodo 5 al 6
Por lo tanto, la duración del proyecto es 38 unidades.
El Problema Dual de la Trayectoria Critica:
El problema dual para el ejemplo numérico anterior es:
Min Z
sujeto a:
-T1 + T2 ³ 9,
-T1 + T3 ³ 6,
-T2 + T3 ³ 0,
-T3 + T4 ³ 7,
-T3 + T5 ³ 8,
-T4 + T5 ³ 10,
-T5 + T6 ³ 6,
-T6 + Z ³ 6,
y todas las variables son ³ 0
La formulación dual sugiere que para cualquier actividad, la diferencia entre el tiempo inicial y terminal exceda la duración de la actividad.
Para resolver el problema dual, a usted podría gustarle probar el Método Algebraico .
También visite la pagina web de
Sitios de Gerencia de Proyectos.
Problema de Flujo de Costo Mínimo
Todos los problemas de red anteriores son casos especiales del problema de flujo de costos mínimo. Al igual que el problema de flujo máximo, este considera flujos en las redes con capacidades. Al igual que el problema del camino mas corto, este considera un costo por flujo hacia un arco. Al igual que el problema de transporte, este permite múltiples orígenes y destinos. Por lo tanto, todos estos problemas pueden ser vistos como casos especiales del problema de flujo de costos mínimo.El problema es minimizar el costo total sujeto a la disponibilidad y la demanda de algunos nodos, y de la conexión superior de flujo a través de cada arco.
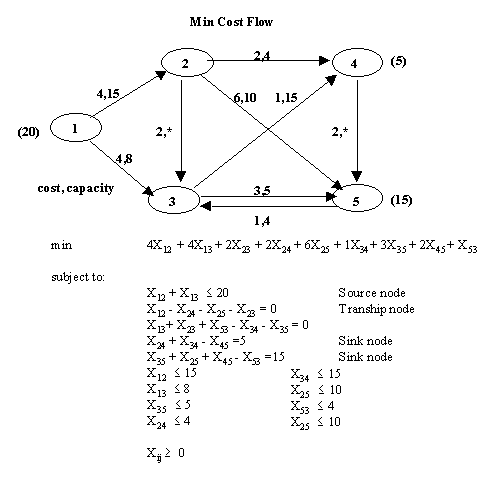
La solución óptima es: X12 = 12, X13 = 8, X23 = 8, X24 = 4, X34 = 11, X35 = 5, X45 = 10, todos los demás Xij = 0. El costo óptimo es $150.
El Dual del Problema de Flujo de Costo Mínimo:
El problema dual para el ejemplo numérico anterior es:
Max 15Y12 + 8Y13 + 5Y35 + 4Y24 + 15Y34 + 10Y25 + 4Y53 + 10Y25
sujeto a:
X2 - X1 + Y12 £ 4, X3 - X1 + Y13 £ 4,
X3 - X2 + Y23 £ 2,
X4 - X2 + Y24 £ 2, X5 - X2 + Y25 £ 6, X4 - X3 + Y34 £ 1,
X5 - X3 + Y35 £ 3, X5 - X4 + Y45 £ 2, X3 - X5 + Y5 £ 1,
Yij £ 0,
y todos los Xi son variables libres.
La formulacion dual sugiere que intentemos asignar flujos a los arcos de forma tal que por cada arco la diferencia en valores en el nodo inicial y terminal, así como también como los valores agregados no excedan el costo asignado a ese arco
Para resolver el problema dual, a usted podría gustarle probar el Método Algebraico .
Análisis de Sensibilidad para los Modelos de Redes
La familia de un clásico problema de optimización de redes incluye los siguientes prototipos de modelos: asignación, camino crítico, flujo máximo, camino mas corto, y transporte. A pesar de que es bien conocido que este tipo de problemas se pueden modelar como programación lineal, normalmente nunca se hace. Debido a la ineficiencia y complejidad relativa del método simplex (primal, dual y otras variaciones) para modelos de redes, este problema es tratado por uno de mas de 400 algoritmos especiales.Esto conlleva a muchas dificultades. Las soluciones de los algoritmos no están unificadas y cada algoritmo usa una estrategia diferente para explorar la estructura especial de un problema específico. Adicionalmente, pequeñas variaciones en el problema tales como la adición de una restricción aparte, o índices múltiples, destruye la estructura especial y obliga a re comenzar el algoritmo. Además, estos algoritmos obtienen soluciones eficientes al costo de la astucia gerencial, como la solución final de estos algoritmos que no tienen la información suficiente para realizar un análisis de sensibilidad.
Otro acercamiento es adoptar el simplex para los problemas de optimización de redes a través del simplex de redes. Esto proporciona la unificación de varios problemas, pero mantiene todas las ineficiencias del simplex así como también la mayoría de las inflexibilidades de las redes para manejar problemas tales como las restricciones aparte. Al igual que el análisis ordinario de sensibilidad (AOS), ampliamente disponible en la tabular simplex, ha sido recientemente transferido a redes simplex.
Advertencia: los soluciones de computadoras para problemas de redes son válidas, sin embargo, los resultados de sensibilidad producidos podrían no ser válidos. Esto se debe al hecho de que, entre otras cosas, estos problemas son PL de enteros, y cualquier restricción en cualquiera de estos modelos es una restricción redundante.
Dado que el “camino” tomado por la rama- atadura (Branch-and-bound), la rama- corte (Branch-and-cut) y otros métodos pueden ser muy diferentes para los pequeños cambios en el valor de los parámetros, hemos desarrollado, vea las referencias, nuevas soluciones algorítmicas, las cuales nos permiten realizar varias formas de análisis de sensibilidad.
Análisis de Perturbación de Costos: : Conjunto de Perturbación General, Análisis de Sensibilidad Paramétrico, Análisis de Sensibilidad Ordinario, Regla del 100%, Análisis de Tolerancia.
Análisis de la Capacidad de Perturbación del Arco: Conjunto de Perturbación General, Análisis de Sensibilidad Paramétrico, Análisis de Sensibilidad Ordinario, Regla del 100%, Análisis de Tolerancia.
Análisis de Perturbación de Oferta y Demanda: Conjunto de Perturbación General, Análisis de Sensibilidad Paramétrico, Análisis de Sensibilidad Ordinario, Regla del 100%, Análisis de Tolerancia.
Programas Lineales Generales de Números Enteros
La programación lineal estándar asume que las variables de decisión son continuas. Sin embargo, en muchas aplicaciones los valores en fracciones podrían tener cierto uso (por ejemplo 2,5 empleados). Por otro lado, como usted sabe, dado que la programación lineal de enteros es difícil de resolver, usted se preguntará ¿por qué preocuparme?, ¿Por qué no simplemente utilizamos la programación lineal estándar y redondeamos la respuesta al entero más cercano? Desafortunadamente, existen dos problemas con esto:
- La solución redondeada podría ser improbable;
- Redondear podría no general una solución óptima.
Max 11X1 + 10X2
S. A. 2X1 + X2 £ 12
X1 - 3X2 ³ 1
Final
GIN X1
GIN X2
El resultado luego de 7 iteraciones es:
VALOR DE LA FUNCION OBEJETIVO
1) 66,00000
VARIABLE VALOR COSTO REDUCIDO
X1 6,000000 -11,000000
X2 0,000000 -10,000000
FILA DÉFICIT O SUPERAVIT
2) 0,000000
3) 5,000000
Si no hubiéramos especificado que X1 y X2 son enteros generales en este modelo, LINDO no hubiera podido encontrar la solución óptima de X1 = 6 y X2 = 0. En vez, LINDO hubiera tratado a X1 y X2 como continuas y la solución sería X1 = 5,29 y X2 = 1,43.
Adicionalmente, note que simplemente redondeando (o aproximando) la solución continua al entero más próximo no genera la solución óptima en este ejemplo. En general, redondeando soluciones continuas no sería óptima y, peor aun, no-factible. Basado en esto, se podría imaginar que sería muy lento el encontrar una solución óptima a un modelo con muchas variables enteras. En general esto es cierto, y usted estaría en una mejor posición si utiliza el GIN solo cuando sea absolutamente necesario.
Como nota final, el comando GIN también acepta un argumento de valor entero en el lugar de la variable nombre. El número corresponde al numero que se quiere que sean variables enteras generales. Estas variables deben aparecer primero en la formulación.. Por lo tanto, en este ejemplo simple, podríamos haber reemplazado nuestras dos perspectivas GIN con la perspectiva simple: GIN 2.
La mayoría de los paquetes comerciales utilizan la rama- atadura (Branch-and-bound) y la rama- corte (Branch-and-cut) para resolver programación de enteros. El primer paso es relajar el problema de programación de enteros a un problema de programación lineal. Sin embargo, algunos software, tales como el CPLEX ejecutarán automáticamente los métodos heurísticos para aproximar la programación lineal para obtener una buena (y confiable) solución a la programación de enteros. La diferencia entre hacer este procedimiento usted mismo y dejar que un solucionador de programación de enteros lo haga, es que este último podría considerar los reembolsos de las restricciones sacrosantas y rechazar cualquier solución aproximada que la viole.
Aplicación de Programación de Enteros Mixtos: Restricciones "Ya sea una-O la otra"
Suponga que una panadería vende ocho tipos diferentes de pasteles. La preparación de las variedades 1, 2, y 3 envuelve un proceso complicado, por lo tanto la panadería ha decidido que es preferible no preparar este tipo de pasteles al menos que se puedan vender por lo menos 10 docenas de las variedades 1, 2 y 3 combinadas. Suponga también que la capacidad de la panadería limita que se produzcan mas de 30 docenas de pasteles, y que la utilidad por unidad j de pastel es Pj dólares. Si dejamos que Xj, j = 1, 2, … ,6 denote el número de docenas de pasteles tipo j a ser horneados, el beneficio máximo puede ser encontrado resolviendo el problema siguiente (asumiendo que la panadería puede vender todo lo que hornea):
Maximizar Z = S Pj Xj
Sujeto a las restricciones: S Xj £ 30
X1 + X2 + X3 = 0, OR, X1 + X2 + X3 ³ 10
Donde todas las variables son no-negativas. La restricción anterior “ya sea una- O la otra” puede ser manejada de la siguiente manera: Deje que y sea una variable 0-1 variable. Luego, el problema equivalente es:
Maximizar Z = S Pj Xj
Sujeto a: S Xj £ 30
X1 + X2 + X3 - 30y £ 0,
X1 + X2 + X3 - 10y³ 10
Xj ³ 0, y = 0, o 1.
Relaciones Condicionales Entre Restricciones
Suponga que, de manera que cierta variable X sea positiva, es necesario que otra variable Y exceda cierto valor umbral. Este enunciado condicional puede ser reformulada como:
Dado que este enunciado condicional puede ser expresado como un enunciado “ o el uno- o el otro” mediante la negación de la hipótesis, el enunciado “ o el uno- o el otro” puede ser expresado como:
Donde M es un número positivo grande.
Restricciones de Encendido-Apagado (On-Off)
Suponga que deseamos que una variable tome el valor a ó de lo contrario sea 0. Es fácil de cumplir esto mediante la siguiente condición: X = da; 0 £ d £1 y d un entero.Obviamente, que si d satisface las dos últimas condiciones, el único valor posible que puede tomar son 0 y 1. Por lo tanto, si d = 0, entonces x = 0, y si d = 1, entonces X = a, tal y como se requería.
Intervalos de Encendido-Apagado(On-Off)
Suponga que queremos que x tome el valor de 0 ó que este en el intervalo fijo entre a y b. Las inigualdades cumplen estos requerimientos: : da £ X £ db; 0 < d < 1 y d entero.Obviamente, si d = 0, entonces x = 0, y si d = 1, entonces x satisface a £X £ b. Estas son los únicos valores posibles para d.
Un Caso de una Variable Discreta Definida Evaluada
Suponga que una variable X tomo solo un valor de un número finito de a1, a2,……, y an. Conjunto:X = a1d1 + a2d2 + … + andn , S di = 1, 0 < di < 1 y di es un entero.
Note que la condición sobre los di's requiere que exactamente uno de ellos debe ser 1 y el resto 0. Y si di = 1, entonces X = ai.
Programas Lineales de Enteros 0 - 1
Utilizando el comando INT en LINDO se restringe una variable a tomar valores 0 ó 1. Estas variables están referidas con frecuencia como variables binarias. En muchas aplicaciones, las variables binarias pueden ser de mucha utilidad para modelar situaciones de todo-o- nada. Algunos ejemplos podrían incluir el tomar en cuenta un costo fijo, construir una nueva planta, o comprar un novel mínimo de cierto insumo para recibir descuento por cantidades.Ejemplo: Considere el Siguiente Problema del Morral
Maximizar 11X1 + 9X2 + 8X3 + 15X4
Sujeto a: 4X1 + 3X2 + 2X3 + 5X4 £ 8, y cualquier Xi es 0 ó 1.
Dado que este es un problema pequeño en tamaño, existen 4 variables que cada una puede tener 2 valores, existen 24 = 16 posibilidades. Probando todas las 16 posibilidades de forma tal de identificar una solución óptima (si es que existe alguna) es un trabajo tedioso. Por lo tanto se debería utilizar el software de Programación Lineal de Enteros para resolver este problema y otros de mayor escala.
Utilizando LINDO, la formulación del problema es:
Max 11X1 + 9X2 + 8X3 + 15X4 S.a. 4X1 + 3X2 + 2X3 + 5X4 £ 8 END INT X1 INT X2 INT X3 INT X4
Luego haga click en SOLVE. El output muestra la solución óptima y el valor óptimo luego de 8 iteraciones de rama- atadura (Branch-and-bound.)
Note que en vez de repetir cuatro veces el INT, se pude utilizar el INT 4. Las primeras cuatro variables aparecen en la función objetivo.
VALOR DE LA FUNCION OBJETIVO
1) 24,00000
VARIABLE VALOR COSTO REDUCIDO
X1 0,000000 -11,000000
X2 1,000000 -9,000000
X3 0,000000 -8,000000
X4 1,000000 -15,000000
FILA DEFICT O SUPERÁVIT PRECIO DUAL
2) 0,000000 0,000000
NO. DE ITERACIONES = 8
El Problema de Viaje del Vendedor
Un vendedor debe visitar las ciudades 1, 2,..n, y su viaje comienza y debe finalizar en Ciudad Hogar. Dejemos que Cij sea el costo de viajar de la ciudad i a la ciudad j, el cual es dado. El problema es determinar una orden óptima para viajar las ciudades de tal forma que el costo sea mínimo.Considere el siguiente Problema de Viaje del Vendedor:
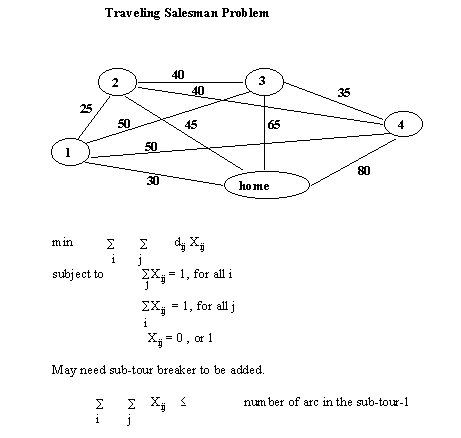
Min 30x01 + 45x02 +65x03+ 80x04 + 25x12 + 50x13+ 50x14 + 40x23+ 40x24 + 35x34 +30X10 +45X20+ 25X21 +65X30 + 50X31 + 40X32 + 80X40+ 50X41+ 40X42 +35X43 Sujeto a: X01+ X02+ X03+ X04=1 X01+ X02+ X03+ X04=1 x10+ x12+ x13+ x14=1 x20+ x21+ x23+ x24=1 x30+ x31+ x32+ x34=1 x40+ x41+ x42+ x43=1 X10+ X20+ X30+ X40=1 X01+ X21+ X31+ X33=1 x02+ X12+ X32+ X42=1 X03+ X13+ X23+ X43=1 X04+ X14+ X24+ X34=1 Todos los Xij = 0, ó 1La solución a este problema de programación lineal produce los sub-viajes (0, 1, 2). Necesitamos introducir un rompedor de viajes tal como
X01 + X10 + X12 + X21+ X02 + X20 £ 2
Agregando esta restricción adicional y resolviendo, necesitamos otro rompedor de viaje, el cual es:
X01 + X10 £ 1,
Agregando este, el camino óptimo es: Ciudad Hogar a la ciudad 1, de ciudad 1 a ciudad 2, de ciudad 2 a ciudad 4, de ciudad 4 a ciudad 3 y de ciudad 3 a ciudad hogar, con una longitud total de 195 unidades.
Aplicaciones al Presupuesto de Capitales
Suponga que una compañía de Investigación y Desarrollo (R & D) tiene una cantidad de dinero disponible para invertir de D Dólares. La compañía ha determinado que existen N proyectos de inversión alternativas y que por lo menos dj dólares deben ser invertidos en el proyecto j si se decide que dicho proyecto amerita la inversión. La ganancia neta que la compañía podría obtener si invierte en el proyecto j es Pj dólares. El dilema de la compañía es que no puede invertir en todos los N proyectos porqueS dj > D. Por lo tanto, la compañía debe decidir en cual proyecto invertir de forma tal de maximizar su utilidad. Para resolver este problema al asesor formula el siguiente problema:
Dejemos que Xj = 1, si la compañía invierte en el proyecto j, y
Xj = 0 si no lo hace.
El monto total a ser invertido es por lo tanto
S dj Xj, y dado que este monto no puede exceder D dólares, tenemos la restricción siguiente:
La utilidad total será S Pj Xj. Por lo tanto la compañía desea un problema 0-1:
Maximizar Z= S Pj Xj
Los hospitales enfrentan constantemente problemas con el horario de trabajo de sus enfermeras. Un modelo de planificación de horarios es un problema de programación de enteros para minimizar el número total de trabajadores sujeto a un número específico de enfermeras durante cada período del día.
Sujeto a: S dj Xj £ D, Xj = 0, OR 1.
Problemas de Horarios
Para utilizar el trabajo como recurso lo más eficiente posible, es importante analizar los requerimientos de mano de obra varias veces al día. Esto es especialmente cierto en grandes compañías en las cuales las demandas de los clientes son repetitivas, pero cambian significativamente durante diferentes horas. Por ejemplo, se necesitan más operadores telefónicos durante el horario comprendido desde el medio día hasta las 2:00p.m. y también desde la media noche hasta las 2:00 a.m. Sin embrago, muchos de estos operadores deben estar en servicio desde tempranas horas de la mañana. Dado que dichos empleados normalmente trabajan jornadas de 8 horas de trabajo, sería posible planificar sus horarios de trabajo de tal manera que una simple jornada pueda cubrir dos o más de estos “periodos pico” de demanda. Mediante el diseño de horarios inteligentes, la productividad del operador incrementaría, generando un grupo de trabajo menos numeroso, y una reducción de gastaos de nómina. Entre otros ejemplos en el cual los modelos de horario de empleados tienen bastante utilidad se encuentran los conductores de autobuses, controladores de tráfico aéreo, y las enfermeras. El siguiente es un ejemplo de problema y desarrollo de un modelo de programación lineal para el horario de trabajo de enfermeras.
|
Dado que cada enfermera trabaja jornadas de 8 horas diarias, el/ ella puede comenzar a trabajar al comienzo de cualquiera de los primeros cinco períodos: 8:00, 10:00, 12:00, 2:00 ó 4:00. En este ejemplo, no consideramos los períodos que comienzan a en horas impares tales como las 9:00, 11:00, etc. Adicionalmente, no se necesita ninguna enfermera que comience a trabajar después de las 4:00, dado que su horario se extendería hasta después de la media noche cuando no son necesarias. Cada período es de 2 horas, por lo tanto cada enfermera que se presente a trabajar en el período t trabajará también t + 1, t + 2, y t + 3 --- es decir, 8 horas consecutivas. La pregunta es: ¿Cuantas enfermeras se deben reportar a trabajar durante cada período de forma tal de cumplir los requerimientos especificados en la tabla anterior? Para modelar este problema, dejemos que Xt sea la variable de decisión la cual denota el número de enfermeras que comenzaran a trabajar en el período t. La fuerza laboral total, la cual deseamos minimizar es S Xt. Durante el período de tiempo 1, por lo menos 10 agentes deben estar al servicio, por lo tanto debemos tener X1 ³ 10. Similarmente, los requerimientos en el período 2 solo pueden ser cubiertos por X1 + X2 ³ 8. De esta forma, escribimos los requerimientos para los períodos restantes. Estos son:
X1 + X2 + X3 ³ 9,
X1 + X2 + X3 + X4 ³ 11,
X2 + X3 + X4 + X5 ³ 13,
X3 + X4 +X5 ³ 8,
X4 + X5 ³ 5,
X5 ³ 3,
Todas las variables son enteros.
Note que X1 no es incluida en la restricción para el período de tiempo 5, dado que las enfermeras que comienzan en el período 1 no están trabando para el período 5. Adicionalmente, observe que podría ser necesario tener un número mayor de enfermeras que el requerimiento en algunos períodos. Por ejemplo, vemos que la primera restricción muestra que el número de enfermeras que comienzan a trabajar en el período 1 debe ser por lo menos 10. Todas estas enfermeras estarán trabajando para el período 2, pero solo 8 agentes las requieren. Por lo tanto igualmente si X2 = 0, existirán 2 enfermeras extras trabajando durante el período 2.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Aplicaciones al Mercadeo
Suponga que existen 5 periódicos diferentes que son publicados en cierto país, cada periódico cubre algunas de las nueve regiones del país, tal y como es mostrado en la tabla siguiente
|
# de Periódico |
Región Cubierta |
Costo por Publicidad |
Beneficios por Publicidad |
|
1 |
1,2,3 |
3 |
12 |
El problema del gerente de mercadeo es encontrar el costo mínimo total de forma tal que la publicidad alcance a todas las áreas del país. Este problema puede ser formulado como una programación lineal de tipo 0- 1:
|
Minimizar C = 3y1 + 4y2 + 3y3 + 7y4 + 5y5 |
|
|
s.a. y1 |
³ 1 (Región 1) |
|
y1 + y2 |
³ 1 (Región 2) |
|
y1 + y2 |
³ 1 (Región 3) |
|
y3 |
³ 1 (Región 4) |
|
y3 + y4 |
³ 1 (Región 5) |
|
y2 + y3 + y5 |
³ 1 (Región 6) |
|
y4 |
³ 1 (Región 7) |
|
y4 + y5 |
³ 1 (Región 8) |
|
y5 |
³ 1 (Región 9) |
|
yj = 0 ó 1, para todos los j's |
La solución óptima es hacer publicidad en los periódicos 1, 3, 4, y 5 con un costo total de $18,00. Esta solución es el costo mínimo asociado con la cobertura en cada una de las nueve áreas.
El Problema de Recorte de Reservas
Suponga que un almacén de maderas ofrece laminas de 10 metros, las cuales son cortadas en 3 metros, 4 metros y 5 metros dependiendo de las exigencias de los clientes. La lámina de madera de 10 metros puede ser cortada en 6 patrones sensibles tal y como se muestra en la tabla siguiente:
|
Patrón # |
3 metros |
4 metros |
5 metros |
Desperdicio (Mts.) |
|
1
|
3
|
0
|
0
|
1
|
|
2
|
2
|
1
|
0
|
0
|
|
3
|
1
|
0
|
1
|
2
|
|
4
|
0
|
1
|
1
|
1
|
|
5
|
0
|
2
|
0
|
2
|
|
6
|
0
|
0
|
2
|
0
|
Existen otros patrones posibles pero que no son sensibles; por lo tanto, se podría cortar una lámina de madera de 10 metros en una de 3 metros y una de 4 metros dejando un desperdicio de 3 metros. Esto no tendría sentido dado que 3 metros de desperdicio podrían ser utilizados como una pieza de 3 metros, así como se muestra en el patrón 2. Si algún cliente ordena 50 láminas de 3 metros, 65 de 4 metros, y 40 de 5 metros. La pregunta sería cuantas láminas de 10 metros se necesitan para cortar estas órdenes, y que patrón se debería utilizar?
Para modelar este problema de decisión, denotemos por yj el número de láminas de 10 metros a cortar de acuerdo al patrón j, j =1, ......, 6. Sea la demanda 50(3) + 65(4) + 40(5) = 610 metros, la cantidad de láminas realmente cortadas es:
10(y1 + y2 + y3 + y4 + y5 + y6),
y por lo tanto el desperdicio total es:
10(y1 + y2 + y3 + y4 + y5 + y6) - 610.
Esto implica que cuando nosotros:
minimizamos y1 + y2 + y3 + y4 + y5 + y6,
el número total de láminas de 10 metros que necesitan ser cortadas, también minimizamos el desperdicio total, y vise versa. El número real de láminas de 3 metros obtenidas en el proceso de cortar es:
3y1 + 2y2 + y3,
y por lo tanto:
3y1 + 2y2+ y3 ³ 50
debe mantenerse con el objetivo de satisfacer la demanda por láminas de 3 metros. De forma similar,
y2 + y4 + 2y5 ³ 65
para satisfacer la demanda de láminas de 4 metros y
y3 + y4 + 2y6 ³ 40
para las láminas de 5 metros. Dado que las variables yj deben ser enteros no negativos,
j = 1, ......, 6, podemos resumir la formulación de cortar las reservas como:
|
P: Min z = y1 + y2 + y3 + y4 + y5 + y6 |
(Láminas de 10 metros) |
|
s.t. 3 y1 + 2y2 + y3 |
³ 50 (Láminas de 3 metros) |
|
y2 + y4 + 2y5 |
³ 65 (Láminas de 4 metros) |
|
y3 + y4 + 2y6 |
³ 40 (Láminas de 5 metros) |
|
yj son enteros no negativos, j = 1, .., 6 |
El ejemplo anterior ilustra una instancia simple del problema de cortar reservas o cortar pérdidas, el cual es ampliamente utilizado cuando se debe minimizar la cantidad de desperdicio. Este ejemplo se refiere a una situación unidimensional (la longitud de la lámina).
Una Aplicación a la Ingeniería: Mezclando Substancias
Una compañía de químicos esta produciendo dos tipos de sustancias (A y B) que requieren tres tipos de materia prima (I, II, y III). Los requerimientos en la composición de las tres sustancias así como también la utilidad son mostrados a continuación:
|
Sustancia |
Composición |
Utilidad |
|
A |
|
10 |
|
B |
|
8 |
La cantidad de material disponible así como también los costos de tratamiento se muestran a continuación:
|
Materia Prima
|
Monto Disponible (Kg)
|
Costos de Procesamiento /Kg
|
|
I
|
400
|
4
|
|
II
|
500
|
5
|
|
III
|
300
|
6
|
El problema de la compañía es encontrar cuanta sustancia producir, y a que nivel de composición de forma tal de maximizar la utilidad.
Dado que tenemos 2 sustancias y tres materiales, introducimos 6 (=2 x 3) variables de decisión xij, i = A, B, y j = I, II, III.
Por ejemplo, xBIII es el monto de materia prima III en la sustancia B. La función objetivo es maximizar la utilidad menos los costos de procesamiento:
max 10(xAI+xAII+xAIII) + 8(xBI+xBII +xBIII) - 4(xAI +xBI) - 5(xAII +xBII) - 6(xAIII+xBIII)
Re-escribiendo esto en términos de las 6 variables de decisión, el problema equivalente es:
max: 6xAI + 5xAII + 4xAIII + 4xBI + 3xBII + 2xBIII
Las restricciones de materiales son:
xAI + xBI £ 400
xAII + xBII £
500
xAIII + xBIII £ 300.
La composición de lasa restricciones son:
0,2(xAI + xAII+ xAIII) ³ xAI
0,1(xAI + xAII + xAIII) ³ xAII
0,2(xAI + xAII + xAIII) £ xAIII
0,4(xBI + xBII + xBIII) ³ xBI
0,5(xBI + xBII + xBIII) ³ xBIIII
De la primera desigualdad en la tabla anterior, se puede derivar la restricción siguiente:
0 £ -0,8xAI + 0,2xAII + 0,2xAIII
Por lo tanto nuestro problema tiene cinco restricciones de la tabla anterior mas tres restricciones de materiales, y una función objetivo. Adicionalmente, requerimos que las variables de decisiones, xij, tome solo valores de enteros no-negativos.
Utilizando su paquete de computadora, la solución óptima es:
xAI = 85, xAII = 42, xAIII = 299, xBI = 306, xBII = 458, xBIII = 1,
con una ganancia total de 4.516.
Esto significa que la compañía debería producir 426 kg de la sustancia A y 765 kg de la sustancia B. De los 400 kg del material I solo 391 kg es usado, mientras que todos los 500 kg del material II y todos los 300 kg del material III son utilizados.
Declaración de derechos de propiedad intelectual: El uso legítimo, según las pautas de 1994
guías de consulta justas del uso para los multimedia educativos,
de los materiales presentados en este sitio Web está permitido para propósitos educativos no comerciales.
Este sitio puede duplicarse,
intacto con esta declaración, en cualquier servidor de acceso público y puede vincularse a cualquier otra página Web. Todos los archivos se encuentran disponibles
en http://home.ubalt.edu/ntsbarsh/Business-stat para el duplicado.
Agradecería recibir comentarios, sugerencias e inquietudes por e-mail. Gracias.