![]()
![]()
To search the site, try Edit | Find in page [Ctrl + f]. Enter a word or phrase in the dialogue box, e.g. "Ln" or "Tan" If the first appearance of the word/phrase is not what you are looking for, try Find Next.
MENU
- Introduction
- A Common Fallacy
- Dividing by Zero Can Get You into Trouble!
- A Sample of the Grown-ups' Arguments Insisting on Dividing by Zero
- What About Taking the Limit?
- Educating the Educators
- Act of Dividing by Zero Is a Meaningless Operation: Forget Its Result
- Origin of the Common Fallacy: Dividing by Zero
- The Need for Numbers
- The Two Notions of Zero
- Is Zero Either Positive or Negative?
- Is Zero an Even or Odd Number?
- Zero is "not there"
- Is 1 a Number or Just a "Unit" for Counting?
- Origin of Infinity and its Symbol
- Other Apparent Difficulties with Zero
- Descartes' Representations of Numbers
- Mathematics Is for Unification and Extensions
- Genealogy of Rational and Irrational Numbers
- The Two Numbers Nature Cares Most: Inventions or Discoveries
- Equation: Its Structure, Roots, and Solutions
- SQRT(4) = +2, and - 2 right? Misplacement of the Sign
- 1 = 2 right? Confusions between Continuous and Discrete Variables
- 1 = 5 right? Confusions between Numbers and Operations
- Recurring Fractions Are Rational Numbers: Confusions between Series and Their Limits
- IEEE Special Floating Point
- 0 = 1 right?
- From Finger Numbers to Computer: The Most Fascinating Journey
- Errant Views and Calculator-assisted Experiment
- Notes, Further Readings, and References
-
A Collection of JavaScript E-labs Learning Objects
Europe Mirror Site Collection
![]()
Introduction
Culturally, our discomfort with the concepts of zero (and infinite) is reflected in such humor as 2 plus 0 still equals 2, even for large values, and popular retorts of similar tone. A like uneasiness occurs in confronting infinity, whose proper use first rests on a careful definition of what is finite. Are we mortals hesitant to admit to our finite nature? Such lighthearted commentary reflects an underlying awkwardness in the manipulation of mathematical expressions where the notions of zero and infinity present themselves. Another fallacy is that the square root of a positive number yields two distinct results. It is not simply a problem of ignorance by young novices who have often been mangled. The same errors are commonly committed by seasoned practitioners. Nay, even educators! These errors can frequently be found as well in prestigious texts published by mainstream publishers.
![]()
A Common Fallacy
A telephone call bringing the obvious error to the attention of the publisher for correction in future editions was met with an astonishing return call from the editor of the text still insisting that 2 ÷ 0 = ¥. Although both the author and editor insist on this computational outcome, they nonetheless somehow decline to continue the Simplex calculation based on this result, contrary to the logic of their conclusion.
![]()
Dividing by Zero Can Get You into Trouble!
This result follows directly from the assumption that it is a legal operation to divide by zero because a - a = 0. If one divides 2 by zero even on a simple, inexpensive calculator, the display will indicate an error condition.
Again, I do emphasis, the question in this Section goes beyond the fallacy that 2/0 is infinity or not. It demonstrates that one should never divide by zero [here (a-a)]. If one does allow oneself dividing by zero, then one ends up in a hell. That is all.
![]()
A Sample of the Grown-ups' Arguments Insisting on
Dividing by Zero
For your thinking pleasure while reading, below is a sample of the grown-ups' arguments that insist on their own justifications for dividing by zero, among others.
Dividing by Zero
- A visitor of this site wrote to me that:
"My argument is that if you can divide zero into a number, and come out with nothing, then you should be able to divide by zero and get nothing. I learned to divide by groups, like 20/5 is 20 put into 5 groups which equals 4 in each group. Well, if you can put nothing into groups., you should be able to put a number into no groups and come out with the same answer."
- Here is yet another persisting argument on a wrong argument we have been taught at early age. However, instead of re-thinking for ourselves with a new-mind eye, unfortunately, some of us still try to justify what are unjustifiable.
"I'm one of those people who doesn't see the difference between saying that "two divided by zero is something that simply can't be done" and "two divided by zero is infinity" because, to me, neither one results in a tangible answer."
This visitor seems to suggest that since both 2/0 and ¥ are meaningless to use, and undefined respectively, therefore, both are the same thing. This is a bad logic, isn't it?
- Another visitor wrote:
"If 2/0 is infinity and undefined, I can accept that because infinity is not defined as anything in particular, but just a number that is too large to compute. I believe this is the same reason that the calculator gives "error" as the result of that division. I am not saying that infinity and undefined are the same concept, but I think they are related."
If the result of dividing by zero (which is a meaningless operation in the first place) by calculator was infinity, then calculator would give you "infinity" not the word "error", or "E", this is so, because only a limited number of letters such as E or the word Error could be formed. Therefore, any illegal operation will default to the error indicator. The Error message means that "the operation you have performed is illegal, such as dividing by zero." Right? The calculator does the mathematical operations, but does not have a mind of its own. Your mind does the interpretation of the results.
Notice also that, although no calculator has human's mind characteristics, however, any calculator has its own "infinity". Infinity for particular calculator is any number greater than the largest number you can display on that particular calculator. "INfinity" is a notion not a number, and it has any meaning if only in relation to what is "finite" in a given situation. Do you understand me?
- One of my favorite visitors of this site, kindly wrote to me that:
"I agree with you that one should never divide by zero. I'm just not convinced that your argument explains why we shouldn't. I feel the 1 = 2 argument is circular in that particular context. It shows that if we assume that division by zero IS infinity then there is no contradiction. There is only a contradiction if division by zero is NOT infinity--the exact opposite of the point you wish to make."
The contradiction comes from an inverse argument. Suppose we allow division by zero then, e.g., one can show 1= 2, because dividing both sides by zero we get ¥ = ¥. As we notice, the first ¥ is not necessarily equal to the second one, otherwise one can do the backward operation and then conclude that 1 = 2.
The same visitor patiently wrote back to me that:
"The two infinities are exactly the same "quantity" just as 6/2 and 3 are the same quantity. How do you mean they are not the same? Infinity plus 100 IS infinity. This can be proven by doing a simple one-to-one mapping of 100+infinity onto itself. Hilbert used his infamous hotel example to show this. The question he was asked is to imagine an infinitely large hotel room with one guest in each and every room. Now imagine a new guest who desires a room. He does not want to share a room. How do you make room for him? The answer is, as in all good puzzles, obvious."
Unfortunately, David Hilbert got into this trap. "This is not mathematics. It is theology," a remark made by Paul Albert Gordan, as reported in Olver's book.
Remember that, the sign ¥ is not for any number it is only for a concept, and "infinite quantity" is unmeasurable by any numerical scale. Therefore, one should never do any kinds of arithmetic operations with it, such as ¥ + 100 = ¥, which gives the silly result, 100 = 0.
Remember also that, a good Logic (including dialogue logic, interrogative logic, informal logic, probability logic and artificial intelligence) is a strong container where we put our Ideas to delivered it to someone else. Therefore, empty logic is useless. Also, having useful ideas but not using strong logic to make it common is dead. One must look for both the container and what it contains. Both are needed good ideas communicated by good logic.
- One of my British colleagues kindly wrote to me that:
"ââ¬Â¦Personally I like the numeral zero as it provokes people to think about their preconceptions. It is possible that people find the notion that you can NOT divide a number by zero unnerving because they like their life organized. Again this could be that when they "do" maths they only consider a "tick" for a correct answer their own reward! Math is far more fun and interesting, don't you think? As a non-maths specialist lecturer I am pleased to point students to consider your web page. Please keep such ideas in the public domain."
Mathematical modeling (i.e., mathematical thinking) is the process of contemplating on the decision problem. In mathematical modeling, mathematics is used as a language to describe, and as a tool to prescribe, and control the decision making process. Therefore mathematical models process aims at describing, prescribing, and controlling our decision making process in all areas of human activities. The cardinal aim of mathematical modeling process is to make our world measurable, calculable, predictable, and thus more manageable.
The decision making process is contemplating on the elements of the decision. By definition of Esthetics, the longer you contemplate on anything the more beautiful that thing is. With respect to beauty of the mathematical modeling process, we distinguish it from other mental manifestations; this process is the results of the perfect apprehension of relations formed by a complexity of elements of the model.
Our high school curriculum should put more emphasis on mathematical modeling rather than maths which in most cases are merely "puzzle solving" which has nothing to do with students lives. This will bring excitement in learning the math language and its applications. Mathematics may be difficult for some students' minds to grasp because of its hierarchical structure: one thing builds on another and depends on it. Roadmapping is the duty of our teachers.
Much of the weakness in our current Math Education system is historical in nature and can be discerned by carefully thinking about the following diagram. It is a simplified 4-step model of using mathematics to solve a problem:
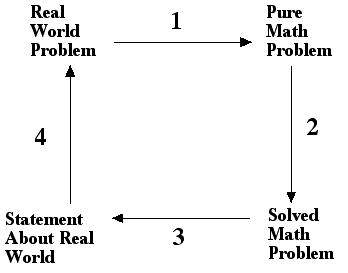
Click on the image to enlarge.
A Mathematics Education SystemStandard estimates are that about 80-percent of Math Education at the K-12 level is focused on part 2 of the above diagram.
Historically, Math Education systems focused on helping students to learn to carry out a number of different types of "step 2" using some combination of mental and written knowledge and skills. It takes a typical students hundreds of hours of study and practice to develop a reasonable level of speed and accuracy in performing addition, subtraction, multiplication, and division on integers, decimal fractions, and fractions. Even this amount of instructional time and practice -- spread out over years of schooling -- tends to produce modest results. Speed and accuracy decline relatively rapidly without continued practice of the skills.
During the past 5,000 years there has been a steady increasing body of knowledge in mathematics, science, and engineering. The industrial age and our more recent information age have lead to a steady increase in the use of "higher" math in many different disciplines and on the job. Our Education System has moved steadily toward the idea that the basic computational aspects described above are insufficient. Students also need to know basic algebra, geometry, statistics, probability, and other higher math topics.
As these topics began to be introduced into the general curriculum, a gap developed between the math that students were learning in school and the math that most people used in their everyday lives. More and more, Math Education focused on learning math topics in a self-contained environment where what was being learned had little immediate use in the lives of the students and little use in the lives of their parents.
A pattern of Math Education curriculum developed in which one of the main reasons for learning the material in a particular course was to be prepared to take the next course. Students developed little skill at transferring their math knowledge and skills into non-math disciplines or into problems that they encountered outside of school. Only a modest number of adults maintain the math knowledge and skills that they initially developed while studying algebra, geometry, and other topics beyond basic arithmetic. That brings us up to current times. Many high schools require students to take three years of math (during their four years of high school) in order to graduate. There is considerable pressure to have all students take an algebra course. The nature of the instruction and the learning in many of these math courses follows the "80-percent on step 2" that has been noted above. Students are now learning the underlying concepts, or how to make use of the math in other courses or outside of a formal school setting.
The language of Mathematics does not consist of formulas alone. The definitions and terms are verbalized often acquiring a meaning different from the customary one. Many students are inclined to hold this against mathematics. For example, one may wonder whether 0 is a number. As the argument goes, it is not, because when one says, I watched a number of movies, one does not mean 0 as a possibility. 1 is an unlikely candidate either. But do not forget that ambiguities exist in plain English (the number's number is one of them) and in other sciences as well. As s matter of fact, mathematical language is by far more accurate than any other one may think of. Do not forget also that every science and a human activity field has its own lingo and a word usage in many instances much different from that one may be more comfortable with.
As a final note in this subsection, the 4-step diagram represents only part of the field of math. For example, it does not include math as a human endeavor with its long and rich history.
- A careful reader wrote:
".. I did understand your "Zero Saga" and I agree wholeheartedly that dividing by zero is completely meaningless. I looked at it this way: When one divides, 13/2 for example, one is basically saying: "what number will you get if you break 13 into two equal parts?" That, of course, will be 6.5. This works for every number except for zero, which isn't exactly a number. If one divides by zero, 4/0 for example, one is saying: "what number will you get if you break 4 into zero equal parts?" That does not make sense although someone can get a little creative as follows. If the question is asking what number will you get if you break 4 into zero equal parts, it can be said that 4/0 implies that the answer is any number of unequal numbers you wish that will add up to 4. That is because zero equal parts=any number of unequal parts.
Zero is a number, and a concept for "nothing."
"What number will you get if you break 4 into zero equal parts?" The answer to this question is that, it is impossible to break anything including numbers into zero equal parts. Right. Try to break an apple into zero equal parts! - On this anther reader wrote:
"..I thought of the question that you asked, "Try to break an apple into zero equal parts!" was a perfect example of this. If you have 1 whole apple and you attempt to divide it into 0 equal parts do you not still have 1 whole apple?"
Have you really attempted in doing so? I am sure you failed, Right? So do not conclude anything.
- Another careful reader wrote:
"Thanks for a great page... I always looked at division by zero using probability/gambling. If you have a 1 in 10 chance of something happening then you have a 1/10 , 0.1, 10% chance of it happening. I always saw this as the number of times something can happen out of the number of possible variations of what can happen. It's inconsistent and can't be defined what odds of 1/0 (1:0)are. Out of 0 events an event happening 1 time is just erroneous and invalid."
- Another reader of this page wrote to me that:
"..It seems apparent that the zero paradox should be broken into to areas: mathematical and physical. Not only is the need to define zero, but infinity as well. For some it is not a question of whether it exists, but merely what the definite result is."
I do agree with you that one must make a clear distinction between the abstract concepts and the concrete concepts as well as their useful implications in modeling process of reality. Therefore, one must engage in investigating mathematical knowledge, especially the relation between conceptual and applied (procedural) knowledge. The distinction between these knowledge types is possible at a theoretical, epistemological and terminological level. One may classified them according to their different approach to a given problem:
Applied knowledge: How to get from where one is to where one wants to go in a finite number of steps.
Conceptual knowledge: How to get from where one is to where one wants to go in a finite or an infinite number of steps, or a leap without any steps at all.
An example of conceptual knowledge would be
Where one is: natural numbers
Where one wants to go: the end of them
How: Infinite number of steps.For the applied knowledge it would be
Where one is: natural numbers
Where one wants to go: the end of them
How: In a finite number of steps depends on what calculator you are using.As you see, conceptuality is subjective while realization is objective. Most conceptuality is metaphysical; while reality is mostly physical.
Now with respect to the last part of your comment, "what the definite result is", one must recall that: being definite has the property of being definable.
- Another reader kindly sent me an email with the subject heading: "To Infinity and Beyond.."
"...... I've been brainwashed since high school to learn that 1/infinity is 0. ..If infinity really is just an abstract concept, not a physical one, then would infinity emerge when we travel at 100% the speed of light?"
What one can reach is finite, thus one can never reach infinity, therefore forget its beyond!
Now, according to the Einstein's theory of relativity, nothing in our universe can accelerate up to the speed of light. Only, under this critical hypothesis (i.e., condition) you might apply the relativity model. Like any mathematical model of reality, this model has its own restriction(s). For example, considering you travel with speed of v, then for each second that passes for you, the clock of the observer, registering1
______
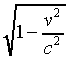
seconds, where the constant c is the speed of light.
Since the condition for using this model requires that v < c, therefore, for the variable v, you cannot choose v = c in the above function. By violating this condition, i.e., substituting v = c, you are making the denominator equal to zero, and then claiming 1/0 is infinity. Thus, my dear reader, infinity does not emerge when you travel at 100% the speed of light. According to this relativity model, you cannot travel 100% the speed of light, unless you become a photon! It is unfortunate that, you violate certain rules and as a result of you own action, you are siting and wondering why and how! You are not alone, on this phenomenon and its many manifestations in our lives.
- Here is a good argument from the real-life practical observations:
" ...Truly fascinating argument. I am also one of those students always taught that any number divided by 0 = infinity. For those that argue that infinity is a correct answer, how can they explain that calculators, typewriters, and computer keyboard do not reflect the infinity symbol?"
- Another reader wrote:
"I enjoyed your discussion very much. I have comments on two issues. I am waiting for your valuable comments.
(1) But, I think "infinity" is not a concept only. We can SEE the "infinity" in our own eyes in broad day light."
But infinity as a number does not exist.
"(2) Possibly, in certain cases 2/0 can be infinity. But, the result is not unique--i.e. it is not the same always. Therefore, the problem lies in the "nonuniqueness" of the result, so that it is not "consistent" (which assumes unique mathematical value) amongst all the cases. If you interpret 20/5 =4 means that if you take 5 oranges from a total of 20 oranges in your fridge you can do it 4 times. Then if you take 0 oranges from 2 oranges (2/0) you can take it infinite number of times (that is, it does not end but surely exists/continues)."
If you "take 0 oranges from 2 oranges", it means 2-0=2. Repeating this operation again and again is nonsense. Once is enough, right? Otherwise eventually you get tired of counting this repetition, beyond that is infinity which you have never reached.
- An engineer kindly wrote, with the the heading: Taking zero as the amount of "error".
"...The problem is in the measurement calculation, not the outcome. Consider 2/(error) which is meaningful no matter how small the measurement error is, unless the error is zero. That is, there is no error.
Your Web site defines such a calculation, showing that some people forget that they are not dividing by zero, but dividing by an error."
You are right, if there is no error, then the act of dividing is meaningless.
- A careful reader wrote:
"After reading your Zero Saga site, I must say I thoroughly enjoyed reading the part where outside individuals commented on your theories and examples. I could understand exactly why they were so adamantly arguing with you because we have been brought up to believe you can indeed divide by zero. However, your examples disproving the division were very persuading and I found myself smiling as individuals got more and more upset as you proved their childhood lessons were indeed fallacy...I guess it shows how unwilling we can be to changing our old ways of thinking...Thanks! "
You are right. Correcting our habit is much harder than learning something correctly in the first place. Habits are indeed the "gravity" of mind. One must be aware of this very formidable and attractive force. What we see is how difficult it is for many of us to correct the habitually wrong conceptions than learning them correctly. What we should do as with anything else is rethink the concept for ourselves. We must be willing to change the way of thinking, the courage to see things differently, and not be stuck in a gravity of the mind situation.
- A frustrated reader wrote:
"I did not find what I was looking for however and am wondering if you could help.
Just like you cannot compute the square root of -1, nor can you compute 1/0 but... a number system including the square root of -1 has been developed and that number system has made the modeling of all sorts of phenomena possible. How come the scientific community is mum on the development of a number system including 1/0?
I am very curious about this development because I foresee it to be the precursor to the next big break through in applied and theoretical mathematics. I can not seem to find an inkling of research out there. I have in two instances in my life come across it. The first was my first year calculus teacher who told the class his research was just that and the second the infamous Tycheon. Any information or help you could provide would be greatly appreciated."I understand your feeling of frustration. There have been many attempts, however, unlike the established applied numerical systems such as complex numbers, these new systems are merely "abstract" with no application. As, you expressed well, within the current concrete numerical systems; the act of dividing by zero is meaningless, thus forbidden.
- The following comments are from Sri Lanka:
I came across your article on the subject of "ZERO" on the internet while trying find out whether it is correct to place a naught in front of single number, for example 05 or 09 instead of 5 or 9. I am from UK living in Sri Lanka and feel somewhat irritated to see noughts being used in front of single numbers. It is seen here on sign boards over shops, i.e. Colombo 03. and in newspaper adverts, i.e. 03 years warrantee. I asked a student for a reason, and his reply was that it looks neater! Another said that is the way they are taught so there is no mistake in what they are writing. But a Sri Lankan who was educated in the 50/60s said that he was never taught to add a naught in front of a number. I do have my theory though, could it be because (some) people are looking for ways of cheating the system and adding a naught stops a 1 being turned into a 10?
Another interesting observation is the use of the word zero in Sri Lanka, which is probably a cultural thing. Using the word zero rather than naught. For example, in the UK we rarely use the word zero. If we were giving out a phone number, we would usually say, my number is oh seven... where here in Sri Lanka they would say, my number is zero seven... The British Telephone directory enquiries service never uses the word zero, always oh.
- Another careful reader wrote:
"I was just reading your article on the zero and although I am not a mathematician to say that anything/0=infinity seems daft. The way I see numbers is rather simplistic. The smaller the number you divide by, the larger the number you get. An infinitesimally small number on the bottom of a fraction will result in an infinitely large result. However, that infinitesimally small number is still a number. Zero denotes nothing. If you divide something by nothing you have NOT divided it."
You are right in stating that " If you divide something by nothing you have NOT divided it." Thank you for your time and sharing your thoughtfulness.
- Another visitor wrote
"I do appreciate your line of explanation to the extent that "division by zero is not to be attempted". Albeit, stating that any defined number divided by zero is infinity is not incorrect. You are questioning " conventional way...". Again how do one define convention? In real analysis, between any two consecutive points there is another point - leading to the statement there can be infinite number of points... So do we say there are "Undefined points??? In my humble opinion, anything divided by zero can be said to be infinity and zero divided by zero is indeterminate!!"
The main problem I have with this line of argument is "the act of dividing by zero" which is meaningless Therefore, it does not make to ask further what is its result, whether it is indeterminate or not.
Mathematical conventions are created for unification of our usual arithmetic operational rules, in most cases.
You are right in stating that ".... there can be infinite number of points...". Which means there are innumerable and even uncountable number of points within this non-empty dense set. It does not say exactly how many. Infinity is a concept not any specific number, therefore one cannot do any kinds of arithmetic operations on a concept nor include it in any arithmetic operations.
You are certainly entitled to keep "... opinion, anything divided by zero can be said to be infinity" as your opinion (and I respect it) but not as a fact and forcing others to agree with your opinion or belief. You may like to visit the Web site How to distinguish among Rumor, Belief, Opinion, and Fact. - A cheerful colleague from Australia wrote that:
"I think from now on, the answer should be:
x/0 = http://home.ubalt.edu/ntsbarsh/zero/ZERO.HTM Really enjoyed your article and comments." Thank you for your time and so much for your kindness to me.
![]()
What About Taking the Limit?
Viewing this issue from the perspective of limits, when considering f(x) = 2/x.
Lim (2/x) as a approaches zero (not equal to zero), neither the left nor the right limit exists. In other words, if one divides 2 by x very small positive number close to zero, the result is a very large positive number, while dividing 2 by a very small negative number close to zero produces a very large negative number. Since the two results are not equal, the limit does not exist. Neither does the limit of each side exist, as shown in the following graphical representation of f(X) = 2/X.

A Graphical Representation of f(X) = 2/X
One of my readers kindly wrote to me that:
"...you wrote, correctly, that the limit of 2/x when x approaches zero does not exist, since it approaches different results from the negative and positive sides. Well, how about lim (2/x2) when a approaches zero? .."
As I pointed out earlier. the lim (2/x) does not exists partly because the right (and the left) limits do not exist. Similarly lim (2/x2) does not exists because it approaches (but never reaching) a very large unspecified positive number.
The same reader wrote back to me that:
"Isn't that the definition of infinity? The same idea that you attack in your paper?"
Infinity is a concept not a number. Do you understand the difference? As I stated before, conceptuality is subjective while realization is objective. Most conceptuality is metaphysical; while reality is mostly physical.
It seems you are a believer of infinity as a number and also a believer that you can reach the limit, and thus missing an important distinction. Approaching is different from reaching. Whatever you reach is not a limit. Therefore, you can take a limit, however you cannot "take it to the limit" as in a popular love song the lover is wishing for. If you can, then it is not a limit, it is merely a numerical functional evaluation.
Chris, a high school student sent me the first quadrant graph of function 1/x, with the following comments:
"..we have just finished my GCSE exams, and we are taught that when x=0, the y value "jumps" off to infinity and the line is very nearly vertical. What do you think about this?
Congratulation Chris for having such an analytical mind and a strong desire to learn more.
The paraphrases from your teacher, such as "jumps off to infinity" and "the line (curve?) is very nearly vertical" are not exact mathematical statements. This is so because they cannot be quantified.
Now let see where the problem is. The function y = 1/x is defined everywhere except at zero. Notice that, you graph misses the other part of the function, which is in the third quadrant, symmetric (to the part you already have) around the origin, for negative x values. Right Chris?
As you see this function is not continuous. That is, to graph it you have to lift you hand from the graph paper to draw the other part. This is a good reason why this function is not defined at point x=0, not even for the limits.
![]()
Educating the Educators
Ball [1990] interviewed 10 elementary and 9 secondary teachers, asking, "Suppose that a student asks you what 7 divided by 0 is. How would you respond? Why is that what you'd say?" What she found was that 1 of the 10 elementary teacher candidates could explain using the meaning of the terms, 2 gave the correct rule, 5 gave an incorrect rule, and 2 didn't know. 4 of the secondary candidates could explain using the meaning of the terms and 5 only gave the correct rule, e.g.; "You can't divide by zero . . . It's just something to remember," but gave no further justification when probed. Some of the teacher who only gave the correct rule were math majors.
Klinger, the author of a book titled "Mathematics for Everyone", which is translated into almost all the European languages, and read by most old-timer educators, wrote:
"Division by zero is a more delicate matter even though it is open stated that the result is "infinity". We do not wish to conduct a philosophical discussion on "infinity" and shall confine ourselves to saying that, if we make a divisor a smaller and smaller decimal value, the quotient will become infinitely great. Thus, if we divide 1 by 1/100 we get 100 and if we divide 1 by one millionth, we get one million." pp.3-4.
In the same book, we read the following, about Zero as a power:
"The power zero has a quite distinctive property of its own. (Yes, we mean zero. Why not?) Let us apply the division of 22 by 22
Now, the division of any quantity whatsoever by itself (for example, the division of 4 by 4) always yields 1, so what we may state the following important rule: Any value (arithmetic or algebraic) taken to the power zero is equal to 1:
and so on" pp.50-51.
Clearly this must not be taken as a proof of "any value ...taken to the power zero is equal to 1". Moreover, what about 00? Is it one too?
When 00 came about? What is its value? One may ask when and how 00 became equal to 1? Since the right-side limit of XX as X approaches positive-zero is one, but its left-side limit does not exists, therefore, one concludes that 00 is undefined.
It seems that Euler was the first to argue for 00 = 1. Newton was the first who used positive, negative, integer, and fractional exponents. However, there are other people who only think in terms of integers, and some of them think 00 = 1 is a good idea. Nevertheless, Since X-1 = 1/X , it follows that X -1. X = = X -1+1 = X0 = 1, however, since X-1 = 1/X is correct for all X except zero, therefore X0 = 1, except for X = 0.
Clearly, 00 is one of those expressions that do not have a definitive meaning but can be given a "contextual" one. Therefore, the value of 00 depends on the context where it occurs; you might wish to substitute it with 1, indeterminate, or undefined. The context in which 00 is taken to be 1 is, e.g., the coefficient of the binomial expansion (X + Y)n, is to be valid even for X = -Y, and for all non-negative integers which includes n = 0. This in turn maintains the beauty of the Pascal Triangular numbers. It is too important to be arbitrarily restricted! By contrast, the function 0n is quite unimportant.
There must be a conviction that mathematics teacher and researchers in mathematics education have much to learn from each other, especially at a time when the school and adult curricula are converging. Based on my experience, I offer the following three distinct headings:
- Recruitment: What can be done to encourage reluctant would-be mathematics teachers to take the plunge?
- Retention: What support do they need to enable them to become sufficiently competent, confident and comfortable with mathematics so that they can teach it to others?
- Re-training: What is it like teaching mathematics without a strong background in mathematics?
Unfortunately, mathematics has been fundamentally depersonalized to "something machines do" and that the meaningful response is that we need always to emphasis that mathematics has little value divorced from imagination. Machines will always do 'imaginationless' mathematics better than humans. But "mathematics imagination meld" is needed by society and it can become a fascinating subject for most children in the classroom.
Too many pupils now think that mathematics is boring. Mathematics can and must be made more fun, more relevant, and more challenging, for pupils and for teachers. The use of Internet interactive technology in the classroom can add a new and precious variety. This variety can help to engage and hold pupils' attention, and can raise the chances that the lesson will have been judged a success. The new interactive technology can help to attract and retain teachers by making the whole process more business-like, more efficient and more effective. However the provision of appropriate hardware, software and training remain expensive and intractable hindrances to progress.
There is a "math" video series [Harlan Meyer, Diamond Entertainment, 1996]. One is called Addition, then Subtraction, Multiplication and, of course, Division. The division segment of the series starts by misspelling the word quotient. Then the "star" of the video shows how to divide by using repeated subtraction; however, she asks "If I have 12 doggy bones and I take away 4 groups of 3 bones, how many will I have left?" She answers herself, "Right, four." But it was the "trick" she claimed for dividing by zero.
Unfortunately, there are many instances like this which sent your blood pressure through the roof. Zero is nothing. So just remember nothing INTO something is nothing. Teaching kids to count is fine, but teaching them what counts is best.

Click on the image to enlarge.
Students Exposure to Zero
One may view "division" as a subtraction operation. When you write 20/5 = 4, what you really mean is that how many times you can subtract 5 from 20? and the answer is 4 times. That is why division is the "inverse" operation for multiplication, which is an addition. That is, 5 x 4 = 20, means, adds to itself 5, 4 times, and you will get 20. So dividing by "0", has no meaning, because the question: how many times you can subtract nothing from something? The question itself makes no sense. The act of dividing by zero is meaningless. Therefore, it does not make to ask further what is its result, whether it is indeterminate or not?
Zero is an important concept, so time should be spent establishing that from early age one has some understanding of zero; zero, nought, nothing - as ever, the language should be varied. In absence of a concept of zero there could have been only positive numerals in computation, the inclusion of zero in mathematics opened up a new dimension of negative numerals. Zero, when used as a counting number (such as zero defect) , means that no such objects are present. A concept and symbol that connotes nullity represents a qualitative advancement of the human capacity of abstraction. As always, concepts are only real in their correct context.
![]()
Act of Dividing by Zero Is a Meaningless Operation:
Forget Its Result
Forget Its Result
For example, if one distributes a pie to 2 people, each would get 1/2. In other words, the distribution takes place across an equal sign among the number specified in the denominator on the left hand side. Since he specifies zero people in the distribution, the transaction is not taken place. The result of interest is on the right-hand side.
It is certainly true that if you do not distribute the pie, you retain it; but when you use an equal sign, you do imply the result of some real transaction to the other side.
Similarly, a / 0 is also meaningless as being the amount of pie the zero people received. This is certainly true for apple pies. The results may differ with other varieties of pies, not all of which have been reviewed!
Once you understand what division is, then there should be little difficulty in understanding why division by zero is not allowed.
A visitor of this site wrote that:
"... but I think it's simply because the division operation is defined in that way. There could be many interpretations for this definition, but there is no reason. As you demonstrated many times, allowing division by zero causes contradiction, thereby making that mathematical system useless. On the other hand, prohibiting division by zero has not yet known to cause any contradiction. If any, that's the only reason why we define division as it currently is."
Division by zero does cause contradiction. That's why we can not divide 2 apples among zero people. It's meaningless, and has no other "interpretations". The act of "distributing" apples cannot be performed.
However, adding zero apples to 2 apples we get 2 apples. Notice that, in addition and subtraction operations we must have the same "dimensions", i.e., not adding up apples with oranges. However, in division operation, this is not a necessary condition, such as in speed, expressed, e.g., as kilometers/hour. It might even have a hybrid dimensionality, like momentum in physics.
" ... for 2/0 = ¥, I think you get all fired up about not much. Of course if there is any implied assertion that ¥ is a number then one gets into all sorts of contradictions that you describe. But I don't think anyone in his right mind considers this. ....the textbook author simply uses the infinity symbol ¥ as a conventional way to denote something that doesn't exist -- something that's impossible (impossible for exactly the reasons you state)."
My concern here is not whether 2/0 = ¥ is true or not. It could have been a hundred times worse than this and I will not lift a finger against it. But, what I'm combating is the act of dividing by zero in the first place, the carelessness of our educators, and not willing to know that they are misleading students. Adding to these, by the way of doubling our difficulties, now it is claimed that ¥ is "a conventional way to denote something that doesn't exist." There is no such conventional usage for ¥. Do you know of any? Whenever, mathematics is distorted and sensationalized, or even pseudo-mathematics is used uncritically, a disservice is done to public understanding of mathematical fact. What I am attempting to signify here is nothing more than this: in applied mathematics dividing by zero is a meaningless operation.in
![]()
Origin of the Common Fallacy:
Dividing by Zero
Dividing by Zero
It may also make you wonder that the word "cifra" in Russian means "written numbers." Similarly, "Ziffer" in German means one single written number; it is used in contrast to a single letter. Zero in German is called 'Null'. French use "zero" as in English. However "chiffre" is the equivalent of the German "Ziffer", a single digit numbers (integers from 0 to 9). Number(s) are called "nombre(s)". The equivalent of "null" is also "nul" in French: "le résultat est nul" translates to "the result is null".
The ancient Egyptians never used a zero symbol in writing their numerals. Therefore there was no function for a zero in writing their numerals. The two applications of the zero concept used by ancient Egyptian scribes
were:
1) as a zero reference point for a system of integers used on
construction guidelines, and
2) as a value that resulted from subtracting a number from an equal number.
It is quite extraordinary that neither the Egyptians nor the Greek were able to create a symbol to represent zero, or nothingness. The conceptual difficulty may have been that the zero is something that must be there in order to say that nothing is there. The Hindu-Arabic numerals were used for written calculations in the West not before the twelfth century, when Arabic texts were translated into Latin. Babylonians also used a zero, approximately at the same time as Egyptians, before 1500 BC. Certainly, zero's application in our base 10 decimal system was a step forward, as logarithms of Napier and others brought into use.
The origin of the fallacy that any number divided by zero is equal to infinity goes back to the work of Bháskara, an Hindu mathematician who wrote in the 12th century that
"3/0 = ¥, this fraction, of which the denominator is cipher is termed an infinite quantity". He made this false claim in connection with an attempt to correct the wrong assertion made earlier by Brahmagupta of India that A / 0 = 0.
Notice that by this fallacy one tries to define "infinity" in terms of zero. Unfortunately, similar practices seem to prevail to the present day. A similar fallacy exists for logarithms of zero which is believed by many to be (negative) infinity.
An author who still advocates that 1/0 = ¥, writes also:
"... (bn - 1)/(b - 1) which is the formula for the sum of a geometric sequence. This has the equivalent form of b(n-1) + ... + b2 + b + 1. If you substitute b=1 in the later expression, the sum is n. Now consider what happens with the first form of the expression when b=1 is substituted. (bn - 1)/(b - 1) = (1n - 1)/(1 - 1) = n. This means that 0/0 = n. Similar proofs exist which show, for example, that 0 = 1".
Remember not to divide by zero. In fact
is correct if and only if b is not 1, and n is a positive integer.
A reader from Canada kindly sent me an email with the subject heading: "Two-dollar bills don't exist"
"Saw your website about division by zero! Excellent!
Here's a little bit of tongue-in-cheek math! Enjoy!
How many dimes are in a quarter? 25/10 = 2.5 Ans. 2 dimes and a nickel remaining
How many two-dollar bills are in a five-dollar bill? 5/2 = 2.5 Ans. 2 two-dollar bills and a one-dollar bill remaining but wait: There is no such thing as a 2-dollar bill.
How many two-dollar bills are in a five-dollar bill? 5/2 = 0 because two-dollar bills don't exist!"
In Canada, you are right on the money!, but not on the 2-dollar US bills! In US we do not have such a dilemma!
![]()
The Need for Numbers
Mathematics is a human endeavor which has spanned over four thousand years; it is part of our cultural heritage; it is a very useful, beautiful and prosperous subject. Mathematics is one of the oldest of sciences; it is also one of the most active; for its strength is the vigor of perpetual youth. Mathematics is also our native language. Numbers are a cultural phenomena, humans invented them to quantify the external world around them. The external world is qualitative in its nature. However, human can understand, compare and manipulate numbers only. Therefore, we use some measurable and numerical scales to quantify the world. This enables us to understand the world by, for example finding any relationship, manipulating, comparing, calculating, etc. That is, to make an Analytical Structured Model for the external world. Then we use the same scale to qualify it back to the world. If you cannot measure it, you cannot manage it. This is the essence of human's understanding and decision making process.
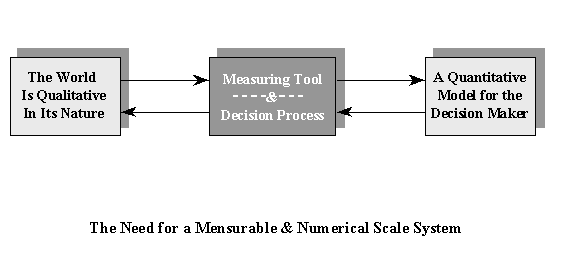
Click on the image to enlarge.
The Need for a Measurable and Numerical Scaling System
The Origin of Algebra: The Vedic Mathematics that is enjoying a vogue in mathematics pedagogy these days is the pre-modern Indian mathematics preserved in Sanskrit; in this category there are a number of mathematical methods many of which were adopted by Muslim recipients and became the basis of our algebra in 13th century. The early use of the Arabic word "al-jabr" was in the sense of "the resetting of bones," and this term was adopted by the early Muslim algebraists as an analogy for what we today call "combining like terms.
Again, The word "algebra" comes from a phrase (in bold below) in the title of an Arab book "Kitab al muhtasar fi hisab al gabr w'al muqubalah." This has been translated as "A compact introduction (book) to calculation using rules of completion and reduction," but some have suggested "al gabr" comes from Babylonian "gabru" meaning solution of an equation, and that "muqubalah" (q reads like k) was its equivalent in Arabic. The book covered simple equations like the one in the preceding section, also quadratic ones involving x2, as well as other areas such as geometry and the division of inheritances.
Its author, Mukhammad ibn Musa Al-Khorezmi (lived about 780-850) was the chief mathematician in the "House of Wisdom", an academy of sciences established in Baghdad by the Caliph Al Ma'mun, son of Harun Al Rashid of "Arabian Nights" fame. The "House of Wisdom" was involved in Al Ma'mun's expedition to measure the size of the Earth, which Al-Khorezmi afterwards estimated to have a circumference of 21000 Arab miles. We are not sure how big the Arab mile was, the actual figure is about 25000 of our miles.
Al-Khorezmi came from the oasis of Khorazem, at the northeast of Persia. He is also credited with helping establish among the Arabs the Indian numbering system, using decimal notation and the zero. Previous systems of writing numbers used letters, like the Roman numeral systems or the cruder ones of the Greeks and Hebrews. When Al-Khorezmi's book on the new system reached Europe, the Europeans called its use "algorism" or "algorithm," a corruption of the author's name. Today "algorithm" means method of calculation, and the rise of computers has led to extensive work on developing efficient computer algorithms The word algebra originated from the title of the book "ilm al-jabr w'almuqabala", written during the 9th century by a Persian Muslim mathematician named al-Khworizimi who wrote in Arabic which was the language of scientific era of the Islamic world. Therefore, the word Algebra derived from the Arabic word Al-jabr meaning combining the like terms.
Finally I would like to quote Johann Carl Friedrich Gauss saying "Mathematics is the queen of the sciences and number theory is the queen of mathematics."
Visit also the following Web sites:
Arabic Numeral System
Babylonian Numerals
Egyptian Numerals
Greek Number Systems
Incas Numerals
Indian Numerals
Mayan Numerals
Roman Numerals
![]()
The Two Notions of Zero
The notion of zero was introduced to Europe in the Middle Ages by Leonardo Fibonacci who translated from Arabic the work of the Persian (from Usbekestan province) scholar Abu Ja'far Muhammad ibn (al)-Khwarizmi (the word "algorithm," Medieval Latin 'algorismus', is a contamination of his name and the Greek word arithmos, meaning "number,: has come to represent any iterative, step-by-step procedure) who in turn documented (in Arabic, in the 7th century) the original work of the Hindu mathematician Ma-hávÃÂral as a superior mathematical construction compared with the then prevalent Roman numerals which do not contain the concept of zero. When these scholarly treatises were being translated by European accountants, they translated 1, 2, 3, ....; upon reaching zero, they pronounced, "empty", Nothing! The scribe asked what to write and was instructed to draw an empty hole, thus introducing the present notation for zero. Hindu and early Muslim mathematicians were using a heavy dot to mark zero's place in calculations. Perhaps we would not be tempted to divide by zero if we also express the zero as a dot rather that the 0 character.
You might ask then how did the Romans do calculations with their numerals notations? Romans typically relied on the Chinese abacus, their version of our modern calculator, visit, e.g., Ancient Civilizations Web site. By using pebbles as counters, there was no need to use Roman numerals. People known as "calculatores" (after "calcule", Latin for "pebbles"), did the math used to tally totals in addition, subtraction, division and multiplication. For us using Roman numerals system to perform arithmetic operations such as division, or multiplication are very difficult if not impossible. In modern days they are used for decorative purposes only.
Zero as a concept, was derived, perhaps from the concept of a void. The concept of void existed in Hindu philosophy and the Buddhist concept of Nirvana, that is: attaining salvation by merging into the void of eternity. Ma-hávÃÂral (born, around 850 BC) was a Hindu mathematician, unfortunately, not much is known about him. As pointed out by George Wilhelm Friedrich Hegel, "India, such a vast country, has no documented history." In the West, the concept of void and nothingness appeared first in the works of Arthur Schopenhauer during the 19th century, although zero as a number has been adapted much earlier.
The Arabic writing mathematicians not only developed decimal notation, they also gave irrational numbers, such as square root of 2, equal rights in the realm of Number. And they developed the language, though not yet the notation, of algebra. One of the influential persons in both areas was Omar Khayyam, known in the west more as a poet. I consider that an important point; too many people still believe that mathematicians have to be dry and uninteresting.
Initially, there was some resistance to accepting this significant modification to the time-honored Roman numerical notation, in particular from the privileged job-secured Roman numerical calculation experts: The Tax Gatherers:
Click on the image to enlarge.
Roman Numerical Calculation Experts: The Tax Gatherers
![]()
Among the trite objections to leaving Roman numerals for the new notation was the difficulty in distinguishing between the numeral 1 and 7. The solution, still employed in Europe, was to use a cross-hatch to distinguish the numeral 7.
The introduction of the new system indisputably marked the democratization of mathematical computation by its simplicity and lack of mystery. Up to then the "abacus" was the champion. Abacus was a favorite tool for a few and praised by Socrates. The Greek's emphasis on geometry (i.e., measuring the land for agricultural purposes, the earth, thus the world geography) so kept them from perfecting number notation system. They simply had no use for zero.
Greeks were not too much interested in arithmetic, believing in inherited nobility of a few, the Greeks had the adage "that arithmetic should be taught in democracies, for it teaches relations of equality, but that geometry alone should be reserved for oligarchies, as it demonstrates the proportions within inequality."
Sacrilegious as it may sound on first impression, the notation of zero is at heart nothing more than a directional separator as in the case of a thermometer. It is, in actuality, "not there." For example, in order to express the number 206, a symbol is needed to show that there are no tens. The digit 0 serves this purpose. Zero became a part of the Natural Numbers System in the last century when Giuseppe Peano puts it in his first of five axioms for his number theory.
One may think of an analogy. Zero is similar to the "color" black, which is not a color at all. It is the absence of color, while the Sun Light contains all the colors.
When we write 10, we mean 1 ten and 0 ones. In some number systems, it would be redundant to mention the 0 ones, because zero means there are no objects there. Place value uses relative positions. So an understanding of the role of 0 as marking that a particular ââ¬Ëplace' is empty is essential, as is its role of maintaining the ââ¬Ëplace' of the other digits. The usage of zero here is more of a qualitative than quantitative. Therefore, it is called an operational zero.
Recently, a visitor of this site kindly wrote to me that:
" I have a basic question about the importance of zero 0 in mathematics. In Mathematics zero has 2 different roles to play... in the articles that I read it was said that zero is important due to both of it's aspect. Whereas I can say by common sense that zero is only useful in case of first aspect i.e. to act as symbol for empty. For second aspect there is no need of zero. To illustrate this lets suppose that in our decimal system we don't have zero ; so it becomes the number system of base 9 (but without zero) because there are only 9 unique symbols to represent any number. They are 1, 2, 3, 4, 5, 6, 7, 8, and 9. Please note that this is 9 base system but without zero. This is important for my discussion. Here by 9 base I mean from 1 to 9 and not from 0 to 8. Here we don't have zero so we can't represent empty set (or emptiness) but that is ok as I am only concerned with showing that the 2nd aspect of zero is not important. For example, we want to represent 104 (base 10) in form of base 9 number system then it is 125 (base 9). So thus any number of any base can be converted to its equivalent symbol (number) of some different base which doesn't provide zero. So what have we lost here? Without zero also we can do as far as positional number system representation is concerned."
- To provide symbol for empty set
- To serve as place holder symbol in positional number system
You are right in that one can express any number in different base systems that exclude zero. However performing any arithmetic operations becomes very tedious, as it is evident, for example with Roman numerical system. That is the main historical reason for the success of decimal numerical system in initiating scientific discoveries, and faster, easier for everyone, and provides more accurate commercial transactions.
Another reader wrote:
"..I am writing a paper for symbolic logic on zero. It seems to be it is 'nothing' in addition/subtraction, but if it is nothing then how can it effect numbers in multiplication? Also as to your comment on 2/0 being meaningless. I am wondering what the answer should be, if it can be more clearly defined), and why."Visit also the Web site:
Here, my dear reader has mixed the two distinct notions of zero: Zero as a number being used in our numerical systems AND as a concept for 'nothing'. As a result of this mixed-up, he is "wondering" at his own mental creature. We used to think that if we know one, we know the other. We are finding out that we must learn a great deal more about "AND".
The introduction of zero into the decimal system was the most significant achievement in the development of a number system in which calculation with large numbers was feasible. Without the notion of zero, astronomy, physics, and chemistry modeling would have been unthinkable. The lack of such a symbol is one of the serious drawbacks in Roman numeral system, beside being difficult to use in any arithmetic operations such as multiplication.
A History of Zero.
![]()
Is Zero Either Positive or Negative?

Click on the image to enlarge.
Adding Zero "as-if" Adding One More Zero
Natural numbers are positive integer numbers. One horse, two trees, etc. However, the arrival of zero caused the inevitable rise of the even more nefarious numbers: The negative numbers.
What about negative numbers? The negative sign is an extension of the number system used to indicate directionality. Zero must be distinguished from nothing. Zero belongs to the integer set of numbers. Zero is neither positive nor negative but psychologically it is negative. The concept of zero represents "something" that is "not there," while zero as a number represents the lowest of all non-negative numbers. For example, if a person has no account in a bank, his/her account is nothing (not there). If he/she has an account, he/she may have an account-balance of zero.
One of my readers kindly wrote to me that:
"...In High school Algebra books they like to teach about numbers. You know whole numbers, natural numbers, rational numbers, irrational numbers, and integers to name a few. The problem that I often run across is where does the zero fit in. For instance 'a positive integer', does this include zero? We know that whole numbers include 0, but it is a positive whole number. Can you clarify some of this for me? Why or why not they are included or excluded. I really wish they would put a little more information into these books as your web sight shows we need it. So I want to thank you, for bringing things into the light.."
You are right, unfortunately some algebra books are confusing on categorizing zero in our numerical systems. However, the accepted and widely use categories for inclusion of zero as a positive number is "non-negative integers", while for excluding it from positive integer the terminology "positive integers" is used. Similarly, for the real numbers involving zero, the following four categories: "positive", "negative", "non-negative" and "non-positive" are being used. The last two categories include zero, while the first two exclude zero, respectively. Therefore, as you see, the first two sets are the subsets of the last two, respectively.
Another visitor kindly wrote to me that:
"I hope you can enlighten me on this one. I've been teaching math for four years but it is only this year that I encountered this problem.
I always thought and believed that zero is neither positive nor negative. It's only when we used the book International Student (7th Ed., by Lial, Hornsby, and Miller, Addison Wesley) that:
when they presented inverse property of addition
they wrote these:
Number Additive Inverse
6 -6
-4 -(-4) or 4
2/3 -2/3
0 -0 or 0
Note: found in page 6.
This is rather confusing to me and to my students because I told them that zero is neither positive nor negative, then why did these authors attach a negative sign on zero?
I looked at other books and I found another one Modern Algebra and Trigonometry (3rd Ed., by Elbridge Vance), that when he also presented Existence of Additive inverses (axiom 6A), in one of his statements he wrote: 0 = -0.
Can you please help me on this one? What could probably be their reason for writing these? These actually confused my students and even me myself in the process.
Thank you very much. I hope you would reply to these question of mine."
I agree with you that it is confusing. It is also a difficult and uncomfortable situation when you as a knowledgeable teacher want to correct the textbook, and your students taking the textbook as the ultimate authority as if it's a Bible. You might like to remind them by mentioning that the purpose of education is critical thinking for oneself.
You are right also in that: The additive inverse of any number is a unique number. Therefore, the additive inverse of 0 cannot be " -0, or 0". (Thanks goodness! they did not include, double zeroes -00, and 00, etc.)
Moreover, the additive inverse of zero is itself. This property of zero also characterizes the zero (i.e., no other number has such nice property).
Furthermore, zero is the Null element for addition. Any operation has a unique Null. The inverse of a Null element for any operation is itself. For example, the Null element for both multiplication and division operations is 1.
![]()
Is Zero an Even or Odd Number?
Most modern textbooks apply concepts such as "even" only to "natural numbers," in connection with primes and factoring. By "natural numbers" they mean positive integers, not including zero. Those who work in foundations of mathematics, though, consider zero a natural number, and for them the integers are whole numbers. From that point of view, the question whether zero is even just does not arise, except by extension.
One may say that zero is neither even nor odd. Because you can pick an even number and divide it in groups, take, e.g., 2, which can be divided in two groups of "1", and 4 can be divided in two groups of "2". But can you divide zero? That's why there are so many "questions."
If you feel that the question if zero is an even number is of no practical value at all, let me quote the following news from the German television news program (ZDF) "Heute" on Oct. 1, 1977:
Smog alarm in Paris: Only cars with an odd terminating number on the license plate are admitted for driving. Cars with an even digit terminating were not allowed to be driven. There were problems: Is the terminating number 0 an even number? Drivers with such numbers were not fined, because the police did not know the answer. Similar phenomenon occurred recently (November 2012) in New York city when the governor's decided to allow cars with even numbers and zero at the end of their number plates to fill up at gas stations on even days the Sandy strong hurricane. It came to the attention of a BBC reporter.
A visitor of this site kindly wrote to me that:
"Is zero odd or even? I suggest a convention, i.e. a useful unproved mechanism which makes me feel better, that zero is indeed Even! I offer two arguments:
A1: "Odd" numbers are spaced two apart. So are "even" numbers. Proceeding downward, 8,6,4,2,0,-2,-4 .. should all be considered Even. While odd numbers 9,7,5,3,1,-1,-3 ... skip over zero in a most stubborn manner.
A2: Let two softball teams play a game, with each player betting one dollar a run to the opposing team. Further presume that no runs are scored (due to beer consumption) and no extra innings are allowed because it got dark.
The final score is zero to zero. If a player is asked by his wife whether he won or lost, he would probably indicate that he "broke even". As the old math teacher said: " Proof? Why any fool can see that."
These are among many issues of how to teach these concepts, say, to kids.
![]()
Zero is "not there"
In some parts of the world, the phrasing "naught" and "aught" are used but it is quite uncommon to hear "zero." All the other digits are correctly enunciated with this one curious exception. However, in the US Army there is an additional curious habit of saying "duece" instead of "two". For example, the M102 105mm Artillery Cannon is called a "One oh Duece" (notice the "oh" therein).
There is also "the Zero Factor about the US Presidents" known as the Zero Factor and Tecumseh's Curse which is the curse of Indian chief Tecumseh which has Killed every U.S. President before the end of their term in office, if they were elected in a year that ended with 0. The first victim of the curse was William Henry Harrison, whose troops killed the Indian chief in 1813 (the zero factor has one exception, i.e., Ronald Reagan who was elected in 1980).
The term "zeroing in on (whatever)" might have originated also with the military. The "zero" in this term might refer to the distance from the last bomb dropped or the last shell fired to some target. The aim is always to try in reducing this distance to zero.
On a roulette wheel, there is the number Zero which is neither Red nor Black. Zero is the GREEN number, for all the cash the house rakes in when it comes up. It is considered neither Even nor Odd.
Is zero a number? Consider the following scene:
Ernie: I've put a number of cookies in that Jar. You can have them if you give me your teddy.
Bert: Great
While Ernie hands over the teddy and looks eagerly in the jar, said:
Bert "Wait a Minute There's No Cookies Here. You Said You Put a Number of Cookies in There"
Ernie: That's right, zero is a number.
It is not uncommon these days to hear, on dating scene, the phrase "get rid of the 'zero' and get yourself a hero". Zero is often used in the description of an undesirable individual as illustrated in following cartoon:

Click on the image to enlarge.
A Sociological Application of Zero
Today zero has a meaning not just of a number, but as the bottom, or failure. He made no baskets, or, he made zero baskets -- meaning he failed to score. Or he gave zero assistance.
If you are familiar with numerology, you notice that there is no zero to work with in the numbers that correlate with the alphabet, strange? Not at all. The absence of zero may suggest that the Pythagorean who first developed the duality between numbers and letters were not aware of the zero notion. The notion of zero is much younger.
In tennis scores, zero is called "love," because zero looks like an egg, the French called it "l'oeuf," which is French for "egg." You may have also noticed the weird numbering in the tennis scores which goes back to medieval numerology, in which 60 was considered a "complete" number (much like 100 is considered a nice round number today). Back in medieval times, tennis's four points were 15, 30, 45 (later abbreviated to 40), and 60, or game.
On the telephone keypad, zero has the honor of representing the operator. There is no zero in most games, such as plying cards (after all who wants to win zero!). Zero is placed at the end of the keypad on the computer and at the bottom of the keypad on the telephone. Is zero the beginning or the end? Notice that on a calculator's keypad the numbers starts with the largest numbers on the top and work their way down to zero. What about the o and 0 being right next to each other on the PC keyboard? Numbers are located three places. First it is located on the keyboard keys with the range 1, 2,...,0; this is the same order that phone keypad. Second, on the right of the keyboard is a calculator-like pad where zero is the last listed number. Finally, there is a list of functions key, however there is no F0 because that could translate into no function and what would be the point of having a key "without" function. There will always be questions about the true meaning and function of zero. Is it the end or the beginning? What does ground zero mean? Some use it as starting point; the military uses it as an ending point.
The resistance against zero can be noted even at the architectural level in buildings where the ground-level is rarely denoted as the zeroth-level as it should be. However, for mathematicians it comes easily to label the floors of a building to include zero, for example, the Department of Mathematics' building at the University of Zagreb in Croatia has floors numbered as -1, 0, 1, 2, and 3. In fact, this is not a particularity of one building but a common practice in modern buildings in large cities such as Buenos Aires. In most European countries the floors are always numbered starting from 0. We do have a special word to say 'ground floor' in a conversation, not using 0, but the elevators will always offer you a "0 button" for the ground floor.
Now is the time to test yourself. Consider 0/0 (zero divided by zero) which of the following takes precedence and why?
By now you should know the answer and the why. For example, for Part C: Any number divided by itself is 1.", which is a true statement for zero. That is 0/0 is also meaningless. One may still argue that 0/0 = 1. Well, if we allow this you end up with some inconsistent results. For example, you end up showing 5 = 1:
5 = 5 . (1) = 5 . (0/0) = [5 . (0)] / 0 = 0/0 = 1
One may say that "I understand why it's considered meaningless to divide a number by 0. But why is the answer considered meaningless when dividing 0 by 0? I think of it as 0 / 0 = x. Zero times x = 0. This is possible because anything multiplied by zero equals zero." The problem with this argument is that "What is the value of x?" It could be any number therefore, one number cannot be equal to so many different numbers. Thus, 0/0 is indeed meaningless. Therefore, teaching our young students that "0/0 = Any Number (AN); this is equivalent to AN x 0 = 0." is wrong. One should never divide by zero. Division by zero is a meaningless operation. How could you divide 3 apples among zero people! How could you divide "nothing" among nobody! You may like to visit and find out what is wrong in the following Web site: Paul, a 3rd grader, divides by ZERO.
One of my readers wrote to me that:
".... what is 0/0? This is equal to any number because when you multiply any number by zero, you get zero. This is why 0/0 is an indeterminate quantity. Is it correct to say x/y = z/y implies x = z unless y = 0?
The main problem I have with this line of argument is "the act of dividing by zero" which is meaningless Therefore, it does not make to ask further what is its result, whether it is indeterminate or not.
Visit also Numbers and Numerical Prefixes, Question Corner
![]()
Is 1 a Number or Just a "Unit" for Counting?
This question is an historical one, because in Euclid "numbers' do not include one. An arithmos is a multitude and hence the opposite of one. The distinction then involves the problem of the one and the many. To the ancients, 1 was never a number. A number was a multitude of units and 1 is a unit, not a multitude. The ancients seem to have identified the multitude with the things themselves in a manner which is difficult to understand.
The ancients Greek had no applied mathematics. The practical and useful mathematics as they had, was developed prior to, independent of and unsupported by any theoretical structure. Moreover, far from supporting useful mathematics, the theoretical systems tended to inhibit its development mainly because they denouncing the treatment of one as a number. This situation persisted through the middle ages and beyond.
You may say that any number, like 1 for example, is simply a "unit" for counting. For example the question, "what do you think of when you think of the number 26?" one may relate it to something, like 26 dollars or 26 shirts, and so on. However, some people the number 26, is 20 + 6, 13(2), 5 2 + 1, and so on. They think of 26 as a number, while others think of 26 as a "unit" for counting.
The Newtonian concept of number which; defines number as the ratio of a magnitude to a unit magnitude of the same kind. The main objection is that the notion of magnitude itself has never been properly defined, and this definition fails in the particular case of complex numbers. Presumably this is because there are no complex magnitudes to provide the necessary ratio.
We are interested in a more objective answer to the question, "is 1 a number or just a 'unit' for counting?" (or as you may phrase the question, "do numbers exist?"). Interestingly enough, some teachers make the statement "I do not think that numbers exist because a number does not refer to anything physical." They say that "a number always refers to a quantity."
One must be aware of the facts that when we use a number it may not have any "dimension" at all. For example, probability is dimensionless. It is a number between zero and one expressing the degree of your belief in occurrence of an event, not any quantity. While we may express for example, the height of a person as ( 5 feet,10 inches) with an absolute error of our measurement of, say 1/5 of an inch (express as length dimension). However, the relative error of the measurement is dimensionless, that is a pure number without any units.
Fermat's Last Theorem (FLT) is another example that illustrates the ability to separate numbers and quantities. The statement x1+y1 =z 1 can be interpreted as follows--there exists a rope of integer length z that can be cut into ropes x and y such that x and y both have integer lengths, and the length of z does not equal the length of x which does not equal the length of y which is non-zero.
The statement x2 + y2 = z2 is commonly called the Pythagorean Theorem, and it can be interpreted as follows -- There exists a square of integer side length z such that two squares, x and y, can be formed from the area of z, where the a right triangle's side lengths of x and y are integers and side length z does not equal side length x which does not equal side length y which is non-zero.
FLT shows that there is no solution to the integer equation x3 + y3 = z3. This can be applied to a quantity as follows-- there are no cube whole number pairs that add to a cube
But what about the fifth dimension? And the sixth? FLT shows that the equation xn +yn = zn has no solutions for all n integer greater than 2, so what is the physical relevance of the statement that x5 + y5 = z5 has no integer solutions?
The only logical explanation is that numbers do not need to refer to physical objects, numbers exist perfectly well on their own. The illustrative examples given in this Section are particularly vivid because they allow you to demonstrate the separation of numbers and quantities to your students at early age.
One of the visitor of this site wrote to me that:
"Not on your web page, but a question regardless. Why is 1 (the number one) not considered prime? I don't consider it a prime for my own reasons, but would like to hear somebody else's views.
My personal prejudice is (in two words) rather shaky.
If I define a prime as a positive integer, divisible only by itself and one; then the number 1 is "special".
Thus, a prime has Two constraints:
A: Indivisibility by any number other than itself, and
B: the trivial Exception of One.
Since 1 is itself, it Is the trivial exception."
A prime number has exactly and only two factors: one and the number. However a composite number has more than two factors. Finally, one is neither prime nor composite because it has only one factor. The question, whether 1 is prime or not goes back to Socrates. The difficulty they had was not considering 1 as a number but a Unit measuring other numbers.
![]()
Origin of Infinity and its Symbol (Â¥ )
In India, when writing about large number, they use Laky. Lash is Sanskrit meaning 100 000. The word appeared first, in non-mathematical works in epic and dharmasastra literature. The word "lacquer" (Lack in German) stems from this word, since huge numbers of "lacquer" lice sit on the "lacquer" tree producing what is now called "lacquer". The word came into scientific use through the early Muslim mathematicians into Medieval Latin and from there into all the European languages.
This sign ¥, or the Western graph for the number 8 positioned horizontally, that is, "the lazy eight", is a sign to denote the idea of infinitely great or infinity, referring to, for example time. The concept of infinity in mathematical systems is expressed by the sign . As far as history is concerned, the most common similar medieval symbol is the snake biting its own tail. It is as if represents a double endlessness or eternity.
On a Roman abacus kept at Bibliotheque Nationale in Paris stands the symbol ¥ on top of its column for 1000. For 1000 the Romans used M an Etruscan letter whose sides were curved, the curious form ¥ , possibly, to convey the concept of a very large number, which ever since the English mathematician John Wallis proposed it in 1655 has been accepted as the mathematical symbol for infinity. He also wrote in the Philosophical Transactions (1671) that "Infinitely means more than any Finite number assignable". Later, the infinite numbers have been discussed in a formal way by George Cantor in 1883. Cantor went to some effort to make connections with ancient and medieval ideas about infinity in his famous series of papers on set theory.
Aristotle considered the infinite as something for which there is no exit in an attempt to pass through it. In his Physics: Book III, he wrote "It is plain, too, that the infinite cannot be an actual thing and a substance and principle."
To facilitate a visual understanding of the infinity concept, you may wish to use the following demonstration for your students: Draw to straight line segments parallel to each other on the board. Make one line segments clearly longer (say, twice) length than the other line segment, as shown in the following graph:
Many students may give you wrong answer and even give give you arguments similar to this one. "Since one line segment is clearly shorter, it can be a multiplication of the other. Therefore it is a subset of the larger one, although both line segments have a large number of points. Two times infinity equals infinity in theory but one is clearly twice the size of the other"
The correct answer is neither of them. Now, you have to convince your students that for every point on one line segment there is exactly one point on the other line segment. To demonstrate this fact, first create a vertex by drawing two other straight lines each passing through the left and right ends of the two line segments. Select a point on either of line segments, and then draw a straight line passing through that point and the vertex. As it is shown in the following graph,
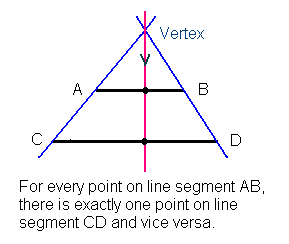
You may also like to pose a questions such as, What do you get when you add up infinitely many positive numbers? What do you think the following adds up to?
Let,
Then, multiplying both sides by 2, we get
Therefore, X = 1. The above sequence adds up to 1.
You may also give a verbal explanation. Suppose you are given a piece of wood of length 1 meter. Cut it into to halves, put aside one half and then cut the other half into two halves again. Repeat this cutting process for eternity. Now, put all the pieces together, what do you get!
Unfortunately, there are teachers who continue misleading students as the following argument illustrates:
But when you start subtracting zeroes, even infinite times, you never get down to zero! One should never divide by zero.
For other current common misconceptions and fallacies on infinity, visit, for example, the Web sites:
INFINITY: You Can't Get There From Here.
![]()
Other Apparent Difficulties with Zero
The notion of zero brings another wearying and yet intriguing questions: Is our current century the 20th century or the 21st century? According to the Holy Scriptures (see, Matthew chapter 2), King Herod was alive when Jesus was born, and Herod died in 4 BC. Does that mean the millennium actually started in 1996?
As you may know, our calendar was improperly set up by a monk in about 525 AD. Since the zero's concept was not available yet, he began the calendar with year 1. Anno domini means "in the year of our lord"; but by starting at 1, the calendar does not correctly reflect the verbal statement. As year one begins, Christ is just born. As year two begins Christ is one year old. The second Century begins with 101 and the second millennium begins with 2002. Still there is a confusion when referring to any particular year in any century. For example, the American Independent achieved in 18th century, but we refer to it as 1776, "as if" it occurred in duting 17th century.
Ordinal numbers, which the Gregorian calendar uses, indicate sequence. Thus "A.D. 1" (or the first year A.D.) refers to the year that begins at the zero point and ends one year later. Think of a carpenter's ruler, if you will; the first inch is the interval between the edge and the one-inch mark. Thus, e.g., the millennium ended with the passing of the two-thousandth year, not with its inception. Cardinal numbers, which astronomers use in their calculations, indicate quantity.
Zero is a cardinal number and indicates a value; it does not name an interval. Thus "zero" indicates the division between B.C. and A.D., not the interval of the first year before or after this point. Continuing with our example, put two rulers end to end: although there is a zero point, there is no "zero'th" inch.
As it stands now, we refer to years with ordinal numbers and to ages with cardinal numbers. Thus a child less than a year old is usually said to be so many weeks or months old, rather than "zero years old." If we changed over to this system for our calendar (referring to the age of our era, rather than to the order of the year), then there would be "zero years" for both A.D. and B.C.! That is to say, the last twelve months before the birth of Christ and the first twelve months after the birth of Christ would be the years 0 B.C. and A.D. 0 respectively. For more on this, you may like also to visit the Web site Zero.
This is quite revealing of the cultural predilections of the time when the calendar was reorganized, first under the Julian scheme undertaken under the auspices of the Roman Emperor, Julius Caesar, after whom the month of July was named, and subsequently under the Gregorian calendar currently in use, which was devised during the reign of Pope Gregory. What is quietly yet magnificently revealed by this now-curious omission is the absence of the notion of zero in the numbering systems then in use. When the notion of zero was subsequently introduced in the west in the Middle Ages, it could hardly have been regarded as feasible to rewrite the entire calendar, if the debate occurred in the first place. Clearly then, our ideas about numbers permeate our culture.
How zero relates to time of day? For instance, what time would be at 12:30 if not for zero.
A visitor of this site asked me "I want to know what the opposite of zero is." Well, not everything has an opposite. The concept of opposite is a human invention in order to make the world manageable, there is no real opposite in nature. Is day opposite of night? Is male opposite of female, or they are complementary to each other? What is the opposite of color blue? Here we must be cautious when we ask about apposite of zero. The difference is between quality (which is a concept) versus quantity (which a number). For example, what is "minus red?" or what is opposite of red? However, in the context of the real line, you can say that the opposite of zero is itself, while the opposite of +2 is -2 with respect to the origin point 0, as both have the same distance from the origin while one in on its right-side and the other on the left-side. This definition is acceptable if you accept the opposite of left is the right. What is the opposite of 1/2? If you say, it's 2, then 0 has no opposite.
Visit also the Web site:
Calendars through the Ages.
![]()
Descartes' Representation of Numbers:
Arithmetic Operations on Negative Numbers
Arithmetic Operations on Negative Numbers
From Analytical-Geometry concepts introduced by Descartes in the 17th century, a real numbers is a point while an interval is the length between two points which is also the absolute value:
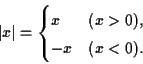
of the difference between two numbers.

Before the introduction of zero to Europe during the Renaissance era, there was no concept of a negative numbers. Even today, for many people, in particular for young pupils the concept of a negative number is hard to understand for strong ontological reasons.
René Descartes was the one who extended real numbers to include negative numbers. The way he accomplished this was by representing numbers on a real number axis as in above figure.
While the number zero had been accepted as a Natural number long ago, in became official much latter. For example, in Sweden school children were to learn that zero is a natural number in their 1960 textbooks.
The positive numbers are on the right of zero (origin), and negative numbers are on the left of zero, which is arbitrary. The reason he chose the right side for positive numbers is because most people are right-handed--not because positive is better. The word "right" might have to do with the use of the English word "right", the Spanish "derecho", etc. to mean certain "positive" things.
Vectors and Numbers: Two Distinct Representations of Numbers: The word "vector" (literally "carrier", from "vectus", past passive participle of "veho" meaning "I carry", and related to the English word "vehicle") was invented by William Rowan Hamilton. However, the useful mixing of mathematics and physics by Isaac Newton's work in describing his three laws of motion is the first powerful tool we now call Analytical Modeling.
Any number represents a point on this real number axis, called O-X axis. For example, point B is +2. It could be represented also as a vector with its origin zero and end point B, with length 2 units, as depicted in the following Figure. Now a question for you: What -3 represents in the following figure? Is it a point?, a number?, a vector (what vector?)?
The four arithmetic operations are well defined by the vector representation of real numbers and appropriate kinds of movements on this real-number axis:
Addition and subtraction operations on numbers can be viewed as the results of movements in certain directions, either to the left or to the right. For example 2 - 3 means starting from the origin O going 2 steps to the right an then 5 steps to the left, you will end up at point -1. Therefore, by vector representation, addition and subtraction easily can be executed on this axis.
Multiplication of a two positive numbers can be considered as a vector multiplied by a scalar. For example, 1.5 time -3 means moving from the origin O toward the same direction (because the scalar 1.5 is positive) the vector -3 and continuing the one half more steps in the same direction, as shown in the following figure, 1.5B = C.
Multiplication of a negative number by a positive number such as -2 times 3, means moving from the origin O toward the opposite direction (because the scalar -2 is negative) of vector +3 and continuing the same amount steps in the same direction. That is moving from the origin O toward the direction of vector -3 and continuing the same amount steps in the same direction.
Division of real numbers may be defined in terms multiplication. That is, dividing two numbers A by B is a number C such that A = B.C.
Multiplication of Two Fractions: A visitor of this site asked me:
"..ââ¬Â¦ When we say that we multiply M by N; we say M X N. In this case we can either say
- N times M
- M times N (N X M)
Here both the statements are true because the answer is the same though imagination differs. From amongst the 2 variables (M and N) one is "quantity" and the another is "number of times" that quantity is repeated. So "number of times" is always a whole number, obviously. This is quite intuitive. BUT "quantity can be either whole number or fraction even, this is also obvious and intuitive because real quantity can be anything; complete number or fraction.
So when we multiply fraction by whole number in the following way (1/2) X 7. This is simple and intuitive. I can say that the fraction 1/2 is being added seven (7) times.
Similarly when we multiply whole number by fraction in the following way 7 X (1/2). This poses problem! Because "number of times" is always a whole number. But since we know that even if we reverse the above thing its going to mean the same i.e., (1/2) X 7. So to make it intuitive we can again say that fraction 1/2 added seven (7) times. This is just the trick to make the problematic statement intuitive since we know that this way also we yield the right result.
BUT THE REAL PROBLEM POSES when both the variables are fractions. For example (1/2) X (3/7). Here how will I imagine what is happening? If I say that the fraction 1/2 is added 3/7 times then this statement itself is erroneous. "Number of Times" is always a whole number. How to imagine this? I am not able to justify myself the above process.ââ¬Â¦."
Notice that, (1/2) X (3/7) can be read as one-half of (3 divided into 7 pieces). That is, half of (one piece of 3 divided into 7 pieces). Each piece is same as a piece of 3 divided by 14, i.e., 3/14. Therefore, (1/2) X (3/7) = [(1)(3)] / [(2)(7)] = 3/14. As expected.
Multiplication of Two Negative Numbers: Another visitor asked me:
"....Why two negative multiplied together give a plus, why not negative."
The oldest source for the rule "a negative number times a negative number gives a positive number" is in Diophantus of Alexandria who applied it in his Arithmetica, without any proof. Numbers with signs (neither plus nor minus) where not developed till the invention of zero. Brahmagupta developed some of colorful rules:
- [The sum] of two positives is positive, of two negatives negative; of a positive and a negative [the sum] is their difference; if they are equal it is zero. The sum of a negative and zero is negative, [that] of a positive and zero positive, [and that] of two zeros zero.
- [If] a smaller [positive] is to be subtracted from a larger positive, [the result] is positive; [if] a smaller negative from a larger negative, [the result] is negative; [if] a larger [negative or positive is to be subtracted] from a smaller [positive or negative, the algebraic sign of] their difference is reversed---negative [becomes] positive and positive negative.
- A negative minus zero is negative, a positive [minus zero] positive; zero [minus zero] is zero. When a positive is to be subtracted from a negative or a negative from a positive, then it is to be added.
- The product of a negative and a positive is negative, of two negatives positive, and of positives positive; the product of zero and a negative, of zero and a positive, or of two zeros is zero.
- A positive divided by a positive or a negative divided by a negative is positive; a zero divided by a zero is zero; a positive divided by a negative is negative; a negative divided by a positive is [also] negative.
- A negative or a positive divided by zero has that [zero] as its divisor, or zero divided by a negative or a positive [has that negative or positive as its divisor]. The square of a negative or of a positive is positive; [the square] of zero is zero. That of which [the square] is the square is [its] square-root.
Multiplication of a negative number by another negative number, such as -2 times -3, means moving from the origin O toward the opposite direction of vector -3 and continuing the same amount steps in the same direction. The movement from the origin O in the direction of +3 and continuing the same amount steps in the same direction will locate us at point +6. Therefore, multiplication of two negative numbers is a positive number.
Trigonometric Functions and Measuring Angles: First, let us understand the definition of the Cosin of an angle, we consider a right triangle, from Greek "orthe gonia", the word "right" for the angle in a rectangle with the English word "rectify" which means to make right. The prefix "rect" is Latin and means "right, straight, or erect". Consider the following right triangle Having a right-angle with sides of length A, B, and hypotenuse length C. The Cosine of angle a equals the length of side B divided the length of the hypotenuse C, that is Cos (a)=B/C. Similarly, the Sine of angle a equals the length of side A divided the length of the hypotenuse C, that is Sin (a)=B/C. However, the Tan of angle a equals the length of side A divided the length of side B that is Tan (a)=A/B. Clearly, Tan (a) = Sin (a)/Cos (a), provided Cos (a) is not zero. The inverses of these functions are Arc's functions, i.e. angles. For example, Arctan or simply ATan denotes the inverse of Tan (a).
I have always equated for my students the word "right" for the angle in a rectangle with the English word "rectify" which means to make right. The prefix "rect" is Latin and means "right, straight, or erect"
For example, what is the cosine of 0? Cos (0) is 1 because if you collapse the angle of the right triangle until the angle a = 0, then the side C (hypotenuse) = side B. Therefore, Cos(0) = 1.
One may extend the one dimensional analytical-geometry concepts in visualization of other algebraic elements,
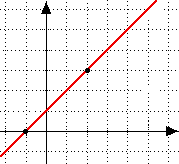
such as equations. For example, the above figure is a graph (i.e., a picture) of equation Y = X + 1, which is a straight line. The slope of the line is the Tan (a), where the angle (a) is that of the horizontal axis making with the line, counterclockwise. For example, the slope of the above line is m = Tan (45) = 1. As another example, if a line has slope of m = -1, then the angle (a) is obtained by the inverse function aTan(-1) = 135 degrees.
The convention of measuring angles in counterclockwise removed any existing ambiguities in communicating and in computations when angles are involved such as functional evaluations in trigonometry. For example, as shown clearly in the following figure:
By the above convention, the angle OB makes with OA is 45 degrees, while the angle OA makes with OB is 135 degrees (not -45 degrees).
Therefore, finally the algebra and geometry are unified by the means of analytical-geometry concepts in last couple of hundred years. This helps overcoming our human visual limitation to see with the eyes-mind and work within space of higher dimensions than the 3-dimensional space we live in.
The 0 kilometer stone monument is near
The Chain Bridge in Budapest, Hungary.
All the road distances in the country are
measured from this monument.
Now back to our earlier question, Why is -2 times -3 = +6? This time, let us consider both numbers as vectors. According to the definition that "The multiplication of two vectors is equal to multiplication of the length of the two vectors times the Cosin of the angle between the two vectors." So (-2)(-3) = 2(3)Cos(0) because the angle between the vector -2 and vector -3 is 0. This is so, since Cos (0) = 1, and both lengths are positive, the multiplication of two negative numbers is always positive.
Another visitor of this site kindly wrote to me that:
"I would like to share with you "my explanation" to state that (-1)(-1) = + 1
Consider (-1)(-1) = X. Since the 17th century it is a rule to do: (-1)(-1) + (-1) = X + (-1). There is the rule a(b+B) = AB+ac. Using it, we get: (-1) [(-1) + 1] = X + (-1). From Descartes: +a + (-a) = 0. Using this new rule we get: (-1) [0] = X + (-1). There is the rule (a)(0) = 0. To accomplish it then (-1) [0] = 0. Then X + ( -1 ) = 0, that implies X + ( -1 ) + (+1) = 0 + (+1), so X = +1, therefore, (-1)(-1) = +1. The result (-1)(-1) = +1 is derived and imposed by the existing rules when the real numbers are extended to include negative numbers.
My best regards and thank you for sharing with us your expertise."
This proof can be generalized for of any two equal negative numbers. However, it will be only a special-case proof. For multiplication of any two negative numbers we have used the vector representation of numbers in this section.
Thanks are yours for your nice algebraic proof.
![]()
Unification and Extensions:
Computing the Lengths, Areas, Volumes, and Hyper-volumes
As pointed out earlier the main achievement in using the Analytical
Geometry concepts is to overcome the limitation of human vision working with dimension higher than 3. For example, a manufacturer who produces more than 3 products has to work in higher dimension when it comes to production decision to determine the optimal production level for each product.
Computing the Lengths, Areas, Volumes, and Hyper-volumes
Length of a line segment with two vertex (x1), and (x2): The length is the absolute value of the determinant:
1 x2
divided by 1! (1 factorial= 1).
Similarly, the area of a triangle is the absolute value of the determinant:
1 x2 y2
1 x3 y3
divided by 2! (2 factorial = 2).
Similarly the volume of a pyramid is the absolute value of the determinant:
1 x2 y2 z2
1 x3 y3 z3
1 x4 y4 z4
divided by 3! (3 factorial 1 ´ 2 ´ 3 = 6).
This nice approach for computing lengths, areas, volumes of a simplex, is now unified and generalized for computing hyper-volumes in k-dimension with the denominator equal to k factorial.
You may like performing your computation using Linear Algebra Calculator.
![]()
Genealogy of Rational and Irrational Numbers
The Pythagoreans held that number, that is to say, the set of positive whole numbers, positive integers, rules supreme in nature and in thought. If that is so, then any two numbers are commensurable; that means that each contains so-and-so many units of the same type, so that the ratio of the two can be expressed as the ratio of two integers. This new number, the fraction is called a rational number. The Pythagorean claim, then, was that all ratios occurring in the natural world are commensurable and can be expressed as rational numbers. Geometrically speaking this means the lines can be divided into exact numbers of (perhaps very small) equal segments; the ratio of the numbers of segments in each line is the ratio of their lengths.
It was known to the early Greek mathematicians that certain "abstract" quantities, such as the square root of 2 are not rational, cannot be expressed as p/q where p and q are integers. The Pythagoreans wanted to hold that quantities of this sort are not part of the real world of natural objects and events. It turned out that a simple application of their famous theorem, i.e. the Pythagoras theorem to be a very real! something shocking to them. One of Socrates questions was "How to double a square?" Certainly the answer is not doubling the side of the square.
There are quantities that are real in the world but, in a genuine sense, are not commensurable. If we can measure the side of a square exactly in terms of some measuring rod, we cannot measure its diagonal precisely with the same rod, no matter how fine the divisions on it. No proper fraction, the ratio of two integers, nor any finite decimal number can express the ratio between the two lengths perfectly. They call such beasts irrational numbers.
Consider the following right triangle with two sides having lengths a, and b respectively, and its hypotenuse having length c. Pythagorean' theorem states that
The following is a simple illustrative and beautiful ancient Indian proof. Consider the following squire having
side length (a + b). Therefore, the area of this square is
However, the whole area contains four right angles each having area of a.b/2, and the middle squire having the area of c2. Therefore,
This gives:
as expected.
One can picture real numbers on the "real" number line, as "points" that fill up all the available positions on the line. But not quite all positions, as we shall see, in the transcendental numbers in the next section in this site.
When one comes, many centuries later, to the question of how to handle irrational properly, or rationally, one might say, within the general concept of what a number is, the matter takes on a rather different complexion. It turns out, for example, that between any pair of rational, no matter how close together they may be, there is an infinite set of irrational.
One may ask what is the solution to the equation X3 - 5 = 0? Perhaps the easiest way to answer is to point out that, for example 1.7099 is not a solution. Indeed, we know this without computation, since 1.70998 is a rational number, and no rational number is a solution of this equation. Hen you may say a solution is X = 51/3. If so, it's vicious circle. Therefore for practical purposes X = 1.70998 is indeed a solution.
Irrational number fascinated the Greeks who where interested also in the geometric interpretation of numbers, such as square root of 2. Nowadays application of square root of 2 is in estimating the real distance traveled across the city going from a location point A to another location B, which has a distance of AB = d measured from the city map.
The above figure illustrates an application of square root of 2 in estimating the real distance between two locations in the modern cities with the distance (d) measured on the map.
As another application of square root of 2, consider the International Metric Standard Paper Sizes (IMSPS) such as A4 which are widely used. In the IMSPS paper size system, all pages have a height-to-width ratio of a square root of two. That is; length of the longer side of the paper divided by the length of of its shorter side is always equal to the square root of two.
This characteristic is especially convenient. For example, when we put two pages of A4 next to each other, then the resulting page will be A3 having again the same height-to-width ratio as shown in the above Figure.
One of my visitors kindly wrote to me: "I have recently read your Internet article on the number zero, which I found very interesting. There are a number of anomalous elements which, perhaps you could explain. The number zero, when delimited on a number line is designated real e. g. ...1.2...0 ...-1...-2... because the values between the integers are included, on the number line. However when 0 is delimited in a collection of integers i.e. 1,2.0, -1, -2, (according to the same publication), it is now a member of the counting numbers, Z. Where does 0 stand in relation to Bertrand Russell's theory of types. Perhaps zero is in the intersection of the number sets real and Z Does this set that putatively contains zero contain itself, which is a fundamental precept of sets in Russell's paradox. Perhaps this is what statisticians really mean by the empty or null set. As you have probably have now guessed I am not a professional mathematician anything beyond A level mathematics is beyond my scope as yet. Not withstanding your comments would be appreciated as well as any corrections for misunderstood concepts. Please do not reply with a full explanation of the theory of types (I will not understand it, my level of lucidity in mathematical proofs is about the level that root 2 is not real). Thank you for reading this communication and reply in layman's terms would be appreciated."
Well, Bertrand Russell was a literary man but not an academic mathematician. Unfortunately, he had thought in many wrong directions and creating many paradoxes useful for him alone. He was engaged in his own daydreamed mathematical logic, for example to prove for him "Why I Am Not a Christian." He was mixing-up the domain of human beliefs with the domain of rational thoughts. This seems odd but that is not my fault. This is the Russell's logic in a nutshell. It seems he had been too good a mathematician not to know exactly when centuries ended. Six hours before midnight on the last day of 1900, he wrote to his American friend Helen Thomas a letter he would later call "boastful," announcing what he thought was the completion of his Principles of Mathematics. "Thank goodness a new age will begin in six hours. [. . .] In October I invented a new subject, which turned out to be all mathematics for the first time treated in its essence. Since then I have written 200,000 words, and I think they are all better than any I had written before."
![]()
The Two Numbers Nature Cares Most:
Inventions or Discoveries
The two numbers that Nature loves most are denoted by p and e. The first is relevant to planets movements around the sun while the second is related to the growth of population of different species.
Inventions or Discoveries
What is p? Planets move around the Sun in ellipsoid shaped-path with major diameter and minor diameter denoted by 2a, and 2b respectively, then the areas they travel are p.a.b. For a circle a = b = r the radius of a circle, therefore the area is p.r2, and its circumference length is 2 p.r . Therefore, p is the ratio of the circumference length of ANY circle divided by the length of its diameter. That is, to have a notion for the numerical value of p, take a robe of any size and make a circle, then circumference/diameter is the p. Using such a geometric argument, Al-Biruni in 11th century suggested that p must be an irrational number.
It is nice to notice that, the derivative of the area of a circle: A = p r2, is the circumference C = 2 p r. Similarly, for sphere the surface is S = 4 p r2, which is the derivative of volume V = 4/3 p r3.
Beside the fact that p is a number, it is also a measurement for an angle in terms of radians. A radian is an angle subtended at the center of a circle by an arc whose length is equal to the radius. Therefore:
In both cases, p is dimensionless, it is just a number, with two related applications.
What is e? The growth of population for every species follows an Exponential law. The size of a population is, after length of time t years is P.e rt , where P is the initial population size and r is the rate of growth of a particular species. The growth rate of human population is about r = 0.019 since World War II.
What is the difference between the accumulations of $1000 invested at a given rate (r) if the interest is compounded daily versus annually?
Suppose you invest $1000, over a period if t-years, with an annual (fixed) interest rate of r, if the interest is added n times per year at the end of each period, then your compounded investment is $1000(1 + r/n)nt.
Now suppose the banker adds the interest at the end of each day then your investment growth faster 1000(1 + r/365) 365t which is very close to 1000e rt which is the compounded investment continuously.
In fact, increasing number of time intervals, e.g. days into half-days, this approximation gets much better, as shown by the following limiting result when the length of each period gets smaller and smaller:
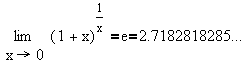
The number e is discovered by John Napier, and it is the base for the so called natural-logarithm, because this number appears frequently in nature. Notice that, the explicit function y = Ln (x), x > 0, is equivalent to the implicit function x = ey, by definition. Moreover, the first and the second function are generally called the logarithmic (Ln) and the exponential (Exp) functions, respectively.
The exact numerical values for these constants are not known, however, it is already available up to 2 million digits after the decimal point: Pi = p = 3.141592654...., and e = 2.718281828.. For example e can be approximated by the following series:
Instead of the above series, one may use the series for e1/2 which converges faster, and you need only then square its sum.
and for p, within one-sixth of one percent, by adding the square root of 2 and the square root of 3. Or using,
or approximating p directly by:
(2) -----------------------------
3 x 3 x 5 x 5 x 7 x 7...
or, using the Andrew John Wiles formula directly:
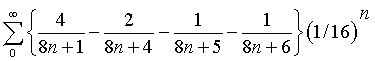
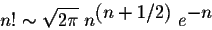
this approximation gets better as n gets larger. Stirling formula has a good number of applications in the Combinatorial counting, and Probability theory.
Since human beings invented the numerical systems, these numbers, which are both beautiful and necessary for nature, become so complicated when expressed in numerical systems for our understanding.
It is unfortunate that many people attach to these numbers various mysteries and religious beliefs. In fact, even mathematicians call them transcendental numbers! Heavenly created! The above explanation, that it is because of human numerical systems, demystifies all these.
A real number which satisfies a polynomial equation with integer coefficients is called algebraic. A real number which is not algebraic is called transcendental.
For example, the Golden Section, which is the way of diving a line of that the ratio of the larger part (b) to the total is the same as the ratio of the smaller (a) to larger, i.e., a/b = b/(a+b). The golden ratio is number = 1÷6180339887... which is an algebraic number but not a transcendental number, since it is the (useful) solution of following equation: X2 - X -1 = 0. It is also interesting to know that p can be approximated as 4 divided by square root of the golden ratio 1÷6180339887....
In general, it is also true that the ratio of two consecutive Fibonacci numbers Ni/Ni-1 tends to the golden ratio., beginning with any couple of numbers. In other words, it is the limit of the ratio of any similar sequence of numbers. That is, let N3 = N1 + N2, and N4 = N2 + N3, and so on, then Ni/Ni-1 tends to the golden ratio, no matter what the original values of N1 and N2 are.
The Golden section ratio has application in Fibonacci search optimization algorithm, and it is often used by artists because of its human aesthetics which is meant to be pleasing to the eye.
Imaginary Numbers: We recall that a real number which satisfies a polynomial equation with integer coefficients is called algebraic. Such as in equation X2 = 1. Now, we may not stop at this simple equation but are curious enough to take matters further by changing the sign on the right-hand side. The new equation X2 = -1 turned out to be the source of much of the discoveries. The solution to this equation is +i, and -i where i is defined by the property that i squared equals -1. The number i is known as the pure Imaginary Number. One of the most beautiful formula in history of mathematics is the Euler's formula involving the five most beautiful numbers: 1, 0, e, i, and the p:
e i p + 1 = 0
That is, the result of raising an irrational number to a power that is an imaginary number can turn out be a natural number. This is obtained from Euler's general and an amazing identity:
e i X = Cos(X) + i Sin(X)
This close connection between trigonometric functions, the natural constant "e", and the square root of -1 cannot be a mere accident; rather, we must be catching a glimpse of a rich, interesting mathematical pattern that for the most part lies hidden from our senses. It is a fact that, without the applications of imaginary numerical system no Engineering Sciences would have been existing as our everyday lives depend on.
The invention, development, and the naming of the numerical systems must be viewed from a historical perspective as a necessity for human to make the world predictable, manageable, and calculable.
Notice that, if a number is not real it does not mean it is unreal. Similarly, since, for example, is not a rational number it does not mean on cannot think of it today. However, there were times when man was wondering about these numbers and therefore named them as it felt confronting them for the first time. This uncomfortable naming of numerical systems is, historically analog when we call the daybreak, the "sunrise!." We are the heirs of our ancestors.
One may wonder if transcendental numbers are so important for nature, why their looks so strange. One must notice that, while numerical systems are human being's inventions, numbers such as p and e, are humans' discovery. Expressing exact values of these numbers in our systems are impossible tasks.
Another beautiful irrational number is: e(p sqrt(163)), which differs from an integer by less than 10-12. Try it on your calculator.
One of the visitors of this site wrote to me that:
"I think the terms Negative, Irrational, Imaginary, and Transcendental numbers are confusing to the layman. I would prefer the following terminology to help make these concepts meaningful to the general public: Consider substituting:
Illogical or "goofy" numbers for Irrational numbers
Pretend or "phony" numbers for Imaginary numbers
Spiritual or religious numbers for Transcendental numbers
The words in quote marks might be more appropriate for grade school application."
I agree with you. The original naming are standard simply because of their historical contexts. These original keywords express the attitude of mathematicians toward these sets of numbers when they tried to make a sense of their meanings and/or their applications.
What is the Benford's Law: Benford's Law states that if we randomly select a number from a table of physical constants or statistical data, the probability that the first digit will be a "1" is about 0.301, rather than 0.1 as we might expect if all digits were equally likely. In general, the "law" says that the probability of the first digit being a "d" is
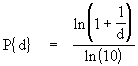
This implies that a number in a table of physical constants is more likely to begin with a smaller digit than a larger digit. This can be observed, for instance, by examining tables of Logarithms and noting that the first pages are much more worn and smudged than later pages.
Frank Benford's law is also called the First Digit Law, First Digit Phenomenon, or Leading Digit Phenomenon. In listings, tables of statistics, etc. This law is closely related to the The Zipf's Law.
Gosh Numbers: The phrase "gosh numbers" is used as a curious form, or speculation of an unknown, or not well understood numbers. For example:
- When the transcendental numbers that pop up in surprising places. For instance, p, e, or Fibonacci sequences, and their notable occurrences in nature are examples for gosh number.
- "The nearest star is trillions of miles away? Gosh!." A number that makes someone say "Gosh!"
- The car mechanic tells you that your car repairs will be, "Gosh, I'd say $500." That is, a usage of the phrase as a guessing number.
- "Minus 40 degrees is the temperature which is the same in both the Fahrenheit and Celsius scales. Gosh." What is "gosh" is that the crossover point between the two scales.
Visit also the following Web sites:
Fascinating Flat Facts about Phi
Fibonacci Numbers and the Golden Section
Golden Section in Art, Architecture and Music
![]()
Equation: Its Structure, Roots, and Solutions
The word "Moaadeleh" meaning "equation" appeared in the writings of al-Khwarizmi together with the common algebraic operations connected to the idea of an equation:
- Jabr: completion, restoration, enforcement, and compulsion
- Muqabalah: posing, opposite, comparison
- Radd: reducing, returning, canceling, and removing
- Takmil: completion.
Equations are any symbolic expression with equality sign, such as X2 = 4. It is good to know that, the word "root" is derived from Sanskrit word "Bija" for "seed" or "root", is the usual term for algebra, where the "root" is the unknown quantity (often called X) that then produces a definite result via the structure of equation.

The definite result (i.e., a fruit) of an equation is called its solution because it satisfies the equation. The above figure depicts the historical analogy developed during the second century between equations' elements and a tree structure. Since by plugging in the numerical value for the root (X), the equation resolves, i.e., it disappears. Hence the numerical value is called a solution, as for example when sugar is mixed with water in making lemonade sugar disappears, making a solution.
![]()
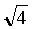 = +2, and - 2 right?
= +2, and - 2 right?
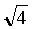 = +2, and - 2 right?
= +2, and - 2 right? Misplacement of the Sign
Solving the equation X2 = 4 has two solutions: X = 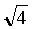 , -
, -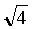 . The number, square root (Sqrt) of 4, is two, therefore, the solution is both X = 2, and X = -2. The symbol ñ is plus OR minus (could be both, but not at the same time). This correct result is distorted when one goes on to write X =
. The number, square root (Sqrt) of 4, is two, therefore, the solution is both X = 2, and X = -2. The symbol ñ is plus OR minus (could be both, but not at the same time). This correct result is distorted when one goes on to write X = 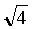 and concludes that this later result is +2, and -2. This is the genealogy of this error. There is a clear distinction here and an important difference which the careful reader will note.
and concludes that this later result is +2, and -2. This is the genealogy of this error. There is a clear distinction here and an important difference which the careful reader will note.
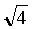 is a positive number that, when you square it, you get 4. While -
is a positive number that, when you square it, you get 4. While - 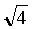 must first, be written as - (
must first, be written as - (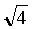 ) and then interpreting the quantity inside the bracket. Do you see the difference?
) and then interpreting the quantity inside the bracket. Do you see the difference?
Unfortunately, this distinction is not still recognized by many instructors. For example, this error is committed by many authors when for example, taking square root of 9. The authors profess to the students that "there are two possible numbers that square to 9, 3 and -3. So, when we take the square root of 9, we put a + and - in front of it." While the first part of this statement is correct, however the conclusion is wrong. When we take the square root of 9, we always get 3, NOT 3 and -3.
![]()
1 = 2 right?
Confusions between Continuous and Discrete Variables
"Here's a problem for you
if you add x x times, then you get x+x+x+...... (x times)
When you take the derivative, then you get 1+1+1+...(x times)
Equals x.
But if you simplify x+x+x..(x times) to get x2,
and take the
derivative, then you get 2x.
Now evaluating both results at point x = 1, you get 1 = 2."
In the second case, the derivative is not defined, because applying the same notation, you cannot take ââ¬Ënx', re label it as ââ¬Ëx.x', and take the derivative of x2 with respect to x, getting 2x, because this would imply taking the derivative of a discrete variable. What this case erroneously purports is taking the derivative of the product (the first term times the derivative of the second term, plus the derivative of the first term times the second term) to get 2x. Applied correctly, the derivative with respect to x would be n. Now evaluating at x = n, then the derivative is in fact x.
![]()
1 = 5 right?
Confusions between Numbers and Operations
"Now try to explain the following steps...
- -5 = -5 (obviously)
- 25 - 30 = 1 - 6 (just the same)
- 25 - 30 + 9 = 1 - 6 + 9 (just added 9)
- (5 - 3)2=(1 - 3)2 (using the binomial rules)
- 5 - 3 = 1 - 3 (square root of 4)
- 5=1 !!!!"
The writer unfortunately confuses the value of a number with the result from taking the square root operation. Taking the square root (an operation) on both sides of (5 - 3)2 = (1 - 3)2 gives ñ (5 - 3) = ñ (1 - 3) or, more simply, (5 - 3) = ñ (1 - 3). These give 2 = ñ 2 Obviously only one is correct. For example, to find one side of a square-shaped area with area of 4 measured in (length unit)2, (equivalently expressed as x2 = 4), taking the square root of both sides gives a result of x = ñ 2. The length, in the context of the problem, is only correctly expressed as x = 2 (length units).
If a2 = b2, what can we say? We can say that |a| = |b|, or if you wish, a = ñ b. Whether either or both are correct is dependent on the context of the problem. Similarly,
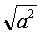 = |a|. Again, there is a clear distinction here and an important difference which the careful reader will note.
= |a|. Again, there is a clear distinction here and an important difference which the careful reader will note.
One of the visitors of this site wrote to me that:
"This would take some faith to believe: ñ (5 - 3) = ñ (1 - 3) or, more simply, (5 - 3) = ñ (1 - 3). These give 2 = ñ 2
I imagine the "truth" is; (5 - 3)2 = (2)2 = 4 = ( - 2)2 = (1 - 3)2 "
It seems to me that in the first line of your comment, you have taken "a part of my argument" out of its context. Now there no need for any "faith to believe". Moreover, you should read 2 = ñ 2, as 2 is equal to +2, OR (not AND) to -2. This understanding is similar, to the reading of: 5 ³ 2. Right?
For the last line of your comment, your imagination is correct. However, you have not taken square root operation yet, which is the main topic of this Section of the site. If you do so, you'll see what you get.
The same visitor, replied back to me that:
"Dear Arsham,
I am impressed with you taking the time to respond to me, and thank you for that. The mathematics I learnt 45 years ago indicated: Let 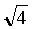 = X. Then X2=4, that is
X2 - 4 = 0. This can be written as (X - 2)(X + 2) = 0, which gives X = 2 or X = -2.
Therefore, X = ñ 2.
= X. Then X2=4, that is
X2 - 4 = 0. This can be written as (X - 2)(X + 2) = 0, which gives X = 2 or X = -2.
Therefore, X = ñ 2.
By this argument, 1 = -1 when you raise both side to the power of 2. Notice that if a = b then a2 = b2. However, a2 = b2 does not imply a = b. Right. So one must be very careful. You are not alone. I do understand in blaming the teacher who robbed your young mind long ago. Your major task in life is to reevaluate all you have been taught, for yourself.
Now, by starting with - 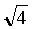 = X, redo your argument, and see for yourself what you end up with. Thank you.
= X, redo your argument, and see for yourself what you end up with. Thank you.
My visitor did his numerical experiment and found out that starting with X = 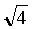 , and X = -
, and X = - 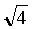 , we end with X = ñ 2. How come, we started with two different numbers and got the same results? The explanation is that X = +2 and X = -2 belong to X =
, we end with X = ñ 2. How come, we started with two different numbers and got the same results? The explanation is that X = +2 and X = -2 belong to X = 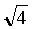 , and X = -
, and X = - 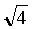 , respectively. Therefore, he concluded, happily that X =
, respectively. Therefore, he concluded, happily that X = 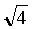 is indeed 2. Thus X =
is indeed 2. Thus X = 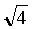 does not give us two different numbers, namely X =+2, and X = -2.
does not give us two different numbers, namely X =+2, and X = -2.
![]()
Recurring Fractions Are Rational Numbers!
Confusions between Series and Their Limits
We have already mentioned rational numbers in this site. Rational Numbers are those real numbers which can be written as p/q where both numbers p and q are integer. The following question is posed by an author is whether or not the recurring fractions such as 0.4444444.... is a rational number, what about 0.9999....?
Confusions between Series and Their Limits
Many instructors argue as follows, Let X = 0.444444..., and then multiplying both sides by ten, we get 10X = 4 + 0.44444... = 4 + X. This gives, X= 4/9, therefore 0.444444... is a rational number! These instructors also claim that in fact all recurring fractions are rational numbers except 0.99999... Because, they argue similarly that, let X = 0.999..., and then multiplying both sides by ten, get 10X = 9 + 0.9999... = 9 + X. This gives, X = 1, therefore it is an integer number not a rational number!
Some teachers use a quick trick that seemed to have the desired effect, at least for students who were willing to admit that:
"Just multiply both sides by 3, and see what you get." 1 = 0.999999...
There are a few misconceptions embedded here. First of all 1 is a rational number too, since it can be written as 1 = 1/1. Moreover, these teachers ignoring the vagueness of the notorious dots used in symbolizing the infinite sequences. The arithmetical operation "to multiply by 3" is defined for the multiplication of finite representations of real numbers and the operation simply is not defined and is not applicable to infinite ones. Indeed, multiplication is begun from the least significant digit, but this digit in an infinite representation simply is absent.
Now let us go back to the main question "is 0.4444.. a rational number or not". The answer is no because 0.444444...is not a well defined number. It is a series. The correct question should have been, "what is the limit of 0.444444....?" Clearly, one can write this recurring fraction as:
4/10 + 4/100 + 4/1000 +.......
Which is a geometric series with the limit equal to (4/10) / [1- (1/10)] = 4/9. Therefore 4/9 is Its limit which is never attainable even increase the number of digits in the fractional portion. Again, 4/9 is not equal to 0.44444... because 0.44444... is not a number, while 4/9 is a well defined number.
If you are old enough, you may remember the once a very popular song "..Take it to the limit one more time..", well, we can never take it to the limit. If you can, then that is not the limit.
Now let's get back to recurring fraction 0.999..... . There is nothing special about this one. Again, we must think of it as a series not a number. This series can be written as:
9/10 + 9/100 + 9/1000 +......
Which is again a geometric series with the limit (9/10) / [1- (1/10)] = 1 which is a rational number. However, this is only a limit, therefore, unattainable, so is 0.99999....
Just as asking yourself: How much is the 1/3 of a dollar bill? Is it 33 cents? Or is it 0.33333.... cents? Similarly, the main question considering topology of the continuum is: What is the meaning of 0.9999...
You may ask "Why were stock prices quoted in eighths of a dollar?" In the 18H century, the American dollar was officially equated in value to the Spanish silver dollar, and the Spanish silver dollar was so large it was literally divided up into eight parts. Due to this, for a long time fractions of an American dollar were also expressed in eighths, especially by America's European trading partners. When the US stock market was established stock prices were quoted in dollars and eighths of a dollar. This practice changed only recently.
Note: A geometric series/sequence/progression is so-called because any term is the geometric mean of its adjacent terms. Archytas called it geometric mean possibly because the tangent OT to a circle from an external point O is the geometric mean of the product OA.OB where points A and B are the intersection points of the circle and the line passing through point O and the center of the circle.)
![]()
IEEE Special Floating Point
The usual implementation of real numbers in today's computers as floating point numbers has the well-known deficiency that most numbers can only be represented up to some fixed accuracy. This means that even the basic arithmetic operations can not be performed exactly, leading to the ubiquitous round-off errors. This is a serious problem in all disciplines where high accuracy calculations are required.
The IEEE has special floating point bit patterns to represent error values. For example 0/0 is NaN (not a number). The IEEE has many NaNs for "indeterminate" quantity. In IEEE standard, 1 divided by 0 is some kind of infinity. It is an indeterminate quantity because it oscillates between + ¥ and - ¥ (depending on whether you are dividing by positive or negative 0).
According IEEE, 1/0 = ¥, (0 as the result of floating point operations) is valid in the real numbers completed by a projective infinity, and is quite useful in many respects. One only needs to realize that the extended real numbers no longer form a "field", so that care is needed with the operations. This has to do with computer bits and bytes which is not enough to represent small or large positive or negative numbers.
The IEEE standard on floating point operations requires 1/0 = ¥, so one finds this nowadays on almost all computers. The inventors of the IEEE standard spent a lot of time to come to a consensus about what to require. It seems to me uncomfortably like the arguments made during IEEE 754 development that 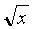 for x negative, should return 0, because in a correct program, x would only be negative because of round off and so it could just as well be zero with no harm done. If you wish to be acquainted with their arguments, visit, for example,
for x negative, should return 0, because in a correct program, x would only be negative because of round off and so it could just as well be zero with no harm done. If you wish to be acquainted with their arguments, visit, for example,
The IEEE Standard for Floating Point Arithmetic, and
Some disasters attributable to bad numerical computing.
![]()
0 = 1 right?
Taking Square Root of Both Sides of an Equality
When the author concludes that 1 = 0, what he (or perhaps she) is really doing is taking the demonstration of a contradiction and proffering it as a solution. Apparent solutions which demonstrate contradictions are in fact proofs that the candidate solution is not a solution after all!
![]()
0 = 1 right?
Manipulation on Divergent Series
We use the same symbol to represent both the infinite series as a formal object or limiting process and also the value of that limit when it exists.
1 - 1 + 1 - 1 + 1 - 1 + 1 - 1 ...
Now consider the following two ways of grouping the terms:
1 + (-1+1) + (-1+1) + (-1+1) ... = 1+0+0+0+... = 1
(1-1) + (1-1) + (1-1)+ (1-1) ... = 0+0+0+0+... = 0
Thus 1 = 0.
Here the error comes from the fact that this is not a convergent series. It is meaningless to manipulate the terms of a divergent series since, by the definition of divergence, the result of such a series is indeterminate. The presenter himself demonstrates why the proffered series is divergent. Why? Because the result of the series is not a fixed, finite value.
Another Example Involving Manipulations on Divergent Series: One of my readers wrote to me that:
Take x/(x+1) for x being any rational number with exception of -1 (We wouldn't like to divide by zero)
This develops as
x/(x+1) = 1- (1/x) + (1/x2) -(1/x3) + (1/x4) - ....
Now take x = 1 then
Becomes: 1/2 = 1-1+1-1+1- ... Without dividing by zero. What did I do wrong ?
I am glad that this reader knows something is wrong. A real number series with general term U(n) converges if |U(n+1)/U(n)| is less than one, which is a necessary condition. The general term for the above series is U(n) = (-1) (n-1)/x(n-1), for n = 1, 2, 3, .... Therefore, |U(n+1)/U(n)| = |1/x| must be less than one. This means that, this series does not converge for any value of x within the open interval of (-1, 1). This means, we are not allowed taking x = 1, as you did and got an strange result.
![]()
0 = 1 right?
Taking Conventions for Proofs
Consider anything to the power of 0: 10 = 1, 20 = 1, ...
In fact, anything to the power of zero equals 1. Thus 00 = 1
Now consider zero to any power. 00 = 0, 01 = 0, ... In this example the writer goes on to state "In fact, zero to the power of anything equals 0. Thus 00 = 0. Thus 1 = 0".
When a new entity in mathematics is defined one must also define its properties, and it's a good idea to make them consistent with the properties of related entities if possible. To make it consistent, sometimes we have to agree on some "conventions".
In order to be able to generalize the algebraic rule that: a (b + c) = a b . a c, for example, even when b = 0, we have to set a 0 = 1. Therefore, it is the convention that a 0 = 1. This convention is needed in order to have consistency in this algebraic operations rule. However, if a = 0, b = 0, c = 0, we no longer have a need for a 0 = 1. Similar argument holds for the algebraic rule that: a (b - c) = a b / a c, for the case when b = c. In both operations, this problem arises only when a = 0, otherwise, in all other cases a 0 = 1 is defined as 1.
Another way of explaining (not, proving!) the convention that, any number raised to the power of zero is 1, except 0, is to look at a pattern...
2 5 = 32
2 4 = 16
2 3 = 8
2 2 = 4
2 1 = 2,
If you follow the pattern, dividing by two each time, the next in the pattern is:
2 0 = 1
Obviously, this will work with other positive numbers. For negative numbers, the signs alternate in the sequence. Therefore, it work for any positive and negative number, except 0. Why not? Because, as we demonstrated earlier, one cannot divide by zero.
As the pattern continues, you can describe negative exponents:
2 -1 = 1/2
2 -2 = 1/4.
A reader asked me:
"What is the meaning of raising a number to the power of a negative number?"
The answer to this question relies on the convention that a 0 = 1, (for all values of a, except zero). Based on this convention, therefore, the operation a -n means 1 / a n, except for a = 0.
Remember that, similar to dividing by zero, zero to the power of any non-positive (which includes zero) is a meaningless operation. You may remember this by the following argument, which is not a proof:
The flaw is that 0-1 = 1/0 which is a meaningless operation. Moreover, the above derivation is not a proof because, to be able to write a-n = 1 / an, we have to use the convention that a0 = 1, for all a except 0. Similarly, an . a-n = an / an, given that by the convention a0 = 1, for all a except 0. Now we realize that by this convention everything looks fine.
Here is a question for you. What is zero to the power of a negative number?
There is another convention is for n factorial (n!), for n being any non-negative integer. It states that zero factorial equals 1, 0! = 1. However, 1! = 1. However, one cannot similarly conclude that 0 = 1 because the one result is arrived at by convention and the other result is a mathematical fact. As with all conventions certain protocols and rules must be followed in arithmetic operations involving zero.
One of the visitors of this site wrote to me with a question: Question: Do the rules and principles you so artfully applied to Zero in your fine web page, apply equally and similarly to the DOUBLE zero?
For example, what is single-zero raised to the double-zero power, and vice versa? Is division by double zero also meaningless and/or forbidden?"
Double zero is still zero. Zero is the only number having such a characteristic.
One of my French colleagues kindly wrote to me that:
"A little remark about the paragraph on 00.
I believe that in your essay you could stress less the 'conventional' aspect of taking 00 = a particular value but insisting more on the analytic limit context since 00 as well as 0/0 or 0Â¥ are encountered when searching for limits of expressions, and to every expression there is a definite answer (in that case 0, 1, an imaginary number, ...) even several (depending on the path to approach the limit value) but not an universal one, as if there was a common value to all functions of any kind.
Similarly about 0! = 1, the origin of this value is an analytic continuation of n! and it is not possible to make it monotonous on [0,1] and it cannot be an argument to deduce 0 = 1 anyway.
One often refers to the 00 = 1 convention as a "combinatorial" one, where as other values are more common in other settings.
Also while it is rare that an extension to 0 of an iterative process such as multiplication or exponentiation has a sound and meaningful interpretation as you often note in your text, it is often very rewarding in mathematics to search for interpretations and settings where an extension of such processes to rational, real and complex numbers can be developed. Among the important and ancient domains where it has been done are differentiation, functional composition and solid revolution.
ââ¬Â¦ thanks for your popularizing efforts, the extensive bibliography you have included"
Clearly, a functional evaluation may not give the same result as taking the limit. For example, the function
As another example, we may ask what is the limit for the function f(X) = XX, with the domain X ³ 0? By taking logarithm, it can be shown that
This limit can be verified using your calculator by evaluating f(X) for an infinitesimal value for X, say X = 0.0000001.
Notice that, this limiting value cannot be taken as a result for 00 by concluding that 00 = 1.
Visit also the following Web site:
Complex Numbers.
![]()
From Finger Numbers to Computer:
The Most Fascinating Journey
The Most Fascinating Journey
Before the advent of a fairly general writing ability the finger numbers were widely used as a universal numerical language. The numbers were indicated by means of different positions of fingers and hands. In a rudimentary way we still occasionally express numbers by our fingers.
Neither the spoken numbers nor the finger numbers have any permanency. To preserve numbers for the purpose of records it is necessary to have other representations. Furthermore, without same memory aids the performance of calculation is extremely difficult.
Ancient Greeks were mostly interested in geometry, since their numerical system was based of denoting numbers to alphabets. The word geometry was derived from measuring (metry) and geo (land, earth). Before 400 B.C., Thales and Pythagoras among others, proved theorems that are still useful and being taught in schools. These ancient mathematicians had their own laptops. A laptop was usually a wooden tray contains smooth sand. They used a finger or a stick to draw and provide their convincing arguments about geometric figures. To restart the laptop, they smoothed the surface and started another session. This was the first laptop. This was the beginning of science then it went to sleep.
The use of a positional system with a zero seems to have made its appearance in India in the period A.D. 600- 800. Around A.D. 800 the system was known among the Muslims in Baghdad and it gradually superseded the older type Arabic numerals. One of the greatest Muslim mathematicians of this time was Mohammed ibn Musa al-Khowarizmi, whose work, Al-Jabr wal-Mqabalah contributed much to the spread of calculations with the new system, first in the Muslim world and later in Europe. This treatise is of interest also because it is believed that its title AL-Jabr has given rise to the term algebra of modern mathematics.
The works of al-Khowarizmi were translated into Latin, and through a perversion of his name the art of computing with Hindu-Arabic numerals became known as algorism This term took on various other forms; in Geoffrey Chaucer work it appears as augrime. The word is still preserved in mathematics where a repeated calculation process is called an algorism.
The numerals took a great variety of shapes some quite different from those now in use, but through the introduction of printing the forms became standardized and have since remained almost unchanged.
The transition to the new numerals was a long-drawn-out process. For several centuries there was considerable ill feeling between the algorismists, the users of the new numerals, and the abacists, who adhered to the abacus ad the Roman numerals. Tradition long preserved Roman numerals in bookkeeping coinage and inscription. Not until the sixteeth century had the new numerals won a complete victory in schools and trade.
It was during the enlightenment era that educational system, such as universities as we know it today flourish. Separation of Church and State allowed individual freedom and after over 2000 (from 400 B.C to the 16th Century) years, at last we went back to pre-Socrates to re-invent science. While pre-Socrates put more emphasis on geometry than arithmetic, the combination of both geometry and arithmetic created by Desecrate, as a Cartesian system is what we now refer to as Analytic Geometry. The analytic geometry was the intellectual foundation for Isaac Newton's models in describing his three laws of motion. His work is the first powerful tool we now call Analytical Modeling. Analytical modeling now dominates all fields of human knowledge, including art, science, and social science.
You may rightly ask, Why we read numbers backwards? As opposed to the Latin writing, the Arabic writing is from right to the left. Therefore, writing a number in Arabic, the smallest positional-digit is written first and the nest smallest, and so on. For example 92 means, 2 ones, and 9 tens. While is English writing, for example it means 9 tens and 2 ones. The beginning of the positions will be to the right of the writer in Arabic, while in the Western work is the opposite is the case. This represents a stage in the introduction of the numerals into the West in which direction has been difficult for children to understand easily.
Arithmetick (a Greek word) is a Science teaching the Manner and Use of Numbering. This science may be wrought diversely, with pen or with counters, and finally the use of computer age in solving large-scale problems by means of distributed, multithreaded, and parallel algorithms. There are many amusing things in the universe, but human's mind is the most amusing of all.
One of my readers from England wrote:
"When I was 11 our class was asked to pick a small integer and present a project on that number. My classmates picked rather obvious small (and positive) values and observed that four seems stable because dogs have as many legs as cars have wheels (and so on). This didn't seem very interesting to me, so I picked zero and focused on the way it doesn't behave well mathematically. I got a poor mark and -- it was explained to me - that this was because I hadn't picked "a proper number".
It is difficult to explain zero to people, even teachers."
You are right, I must say unfortunately. ". . . if one were to place two points on a map, students would find it easy to state the direction and length of the line connecting them (5" running SE-NW). But what if the two points were on top of one another? The length is easier to discern than the direction. The correct answer is that the solution is undefined (and the question silly). The 2/0=INF crowd are essentially saying that the vector exists in the solution domain of valid compass points and might be inclined to nominally place it in the region of the northern magnetic pole and answer N-S. This is an answer that is measurably more inferior to the one given by the students who suggest that perhaps the vector in question points in ALL compass directions (for at least the answer matches the question for meaninglessness)."
A vector has 3 components: An origin, a direction, and a (nonzero) length. Therefore, "two points were on top of one another" does not represent a vector. "ââ¬Â¦I have a question for you. If percentages are hundredths-of, what is the name of the scale that measures in thousandths? It is the scale used for chemical purity, such as with ammonia solution (strong when 990) and silver (pure grade at 995)."
Analog to percent you may call this scale 'permilli', as in millimeter which is one of thousandths-of a meter. "The practical problems with zero cropped up in the early days of flight simulators. The problem was that if the plane was plummeting perfectly straight down (or climbing away from the center of the Earth, like a rocket) this vector no longer denoted which way it faced because the lateral vector of acceleration had zero length. The consequence was that computational failure prorogated through the calculations and the program would crash..."
A vertical line has no slope. It seems to me that the program did not include occurrence of such an event. "ââ¬Â¦it's particularly weird that 00 = 1 (when all other zero-to-the-something-powers are zero). Additionally, as 102 is 100, it follows that 100 root 2 is ten (which it is). Analogously, with 100 = 1, 1 root zero is 10 (or 6, or 5, or -3). But are we not allowed to root-zero things the same way we must refrain from dividing with it?"
First of all, 00 is Not 1, it's undefined. However, 100 is 1 by convention only, not by any proofs. However, the reverse operation is not permitted. Even for non-zero power in your other example, 102 is 100, which can be written equally as 102 = 100 = (-10)2. Clearly, one cannot conclude 10 = -10 from it. Right? Notice that, there is not even any convention for dividing by zero. "Thanks for your page on these controversial values; I experienced a non-zero measure of enjoyment while reading it."
Delighted.
![]()
Errant Views and Calculator-assisted Experiment
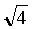 and other examples as experiments in every one of his classes. Inevitably, almost half of the class responds incorrectly. We would suggest that readers who teach try a similar experiment in their own classes both to confirm the occurrence of these errors as well as to apply the appropriate teaching corrective. While the hour is late, there may still be time to save our civilization.
and other examples as experiments in every one of his classes. Inevitably, almost half of the class responds incorrectly. We would suggest that readers who teach try a similar experiment in their own classes both to confirm the occurrence of these errors as well as to apply the appropriate teaching corrective. While the hour is late, there may still be time to save our civilization.
Here is a basic calculator for assisting you to perform numerical experimentation, for at least a few hours (as students do in, e.g. Physics labs.). This serves as a learning tool for the fundamental mathematical concepts and functions, including trig functions (all entries for angles must be between 0 and 360 degrees), we have covered, which are highlighted in this site
Therefore, the materials presented in this site may also serve as a manual for this calculator. The main purpose of performing experimentation is to enhance your learning, therefore if you get any surprising display results, then you must think carefully for the "why?" The answers can be found in this site. Right?
Unfortunately, most of Java-based calculators available on the Web produce wrong results.
To exercise your knowledge, find out what is wrong with:
- this very simple Calculator, or this Calculator.
- what about Scientific Calculator, or Graph It Calculator.
- what about this Scientific Calculator [e.g., try to find out the angle of a line with slope, say m = -1, i.e., tan-1(-1)?], or using Virtual calculator.
- try this Scientific/Engineering Calculator for Tan(90), same for this Physics Computer, or Astro-Physical Calculator.
- what do you think of Carl's Calculator
![]()