To search the site, try Edit | Find in page [Ctrl + f]. Enter a word or phrase in the dialogue box, e.g. "parameter" or "probability" If the first appearance of the word/phrase is not what you are looking for, try Find Next.
Topics in Statistical Data Analysis
![]()
Binomial , Multinomial , Hypergeometric , Geometric , Pascal , Negative Binomial , Poisson , Normal , Gamma , Exponential , Beta , Uniform , Log-normal , Rayleigh , Cauchy , Chi-square,
Weibull , Extreme value , t distributions .
Common Discrete Probability Functions
P-values for the Popular Distributions
![]()
Why Is Every Thing Priced One Penny Off the Dollar?
A Short History of Probability and Statistics
Different Schools of Thought in Statistics
Bayesian, Frequentist, and Classical Methods
Rumor, Belief, Opinion, and Fact
What is Statistical Data Analysis? Data are not Information!
Data Processing: Coding, Typing, and Editing
Type of Data and Levels of Measurement
Variance of Nonlinear Random Functions
Visualization of Statistics: Analytic-Geometry & Statistics
What Is a Geometric Mean?
What Is Central Limit Theorem?
What Is a Sampling Distribution?
Outlier Removal
Least Squares Models
Least Median of Squares Models
What Is Sufficiency?
You Must Look at Your Scattergrams!
Power of a Test
ANOVA: Analysis of Variance
Orthogonal Contrasts of Means in ANOVA
Problems with Stepwise Variable Selection
An Alternative Approach for Estimating a Regression Line
Multivariate Data Analysis
The Meaning and Interpretation of P-values (what the data say?)
What is the Effect Size?
What is the Benford's Law? What About the Zipf's Law?
Bias Reduction Techniques
Area under Standard Normal Curve
Number of Class Interval in Histogram
Structural Equation Modeling
Econometrics and Time Series Models
Tri-linear Coordinates Triangle
Internal and Inter-rater Reliability
When to Use Nonparametric Technique?
Analysis of Incomplete Data
Interactions in ANOVA and Regression Analysis
Control Charts, and the CUSUM
The Six-Sigma Quality
Repeatability and Reproducibility
Statistical Instrument, Grab Sampling, and Passive Sampling Techniques
Distance Sampling
Bayes and Empirical Bayes Methods
Markovian & Memory Theory
Likelihood Methods
Accuracy, Precision, Robustness, and Quality
Influence Function and Its Applications
What is Imprecise Probability?
What is a Meta-Analysis?
Industrial Data Modeling
Prediction Interval
Fitting Data to a Broken Line
How to determine if Two Regression Lines Are Parallel?
Constrained Regression Model
Semiparametric and Non-parametric Modeling
Moderation and Mediation
Discriminant and Classification
Index of Similarity in Classification
Generalized Linear and Logistic Models
Survival Analysis
Association Among Nominal Variables
Spearman's Correlation, and Kendall's tau Application
Repeated Measures and Longitudinal Data
Spatial Data Analysis
Boundary Line Analysis
Geostatistics Modeling
Data Mining and Knowledge Discovery
Neural Networks Applications
Information Theory
Incidence and Prevalence Rates
Software Selection
Box-Cox Power Transformation
Multiple Comparison Tests
Antedependent Modeling for Repeated Measurements
Split-half Analysis
Sequential Acceptance Sampling
Local Influence
Variogram Analysis
Credit Scoring: Consumer Credit Assessment
Components of the Interest Rates
Partial Least Squares
Growth Curve Modeling
Saturated Model & Saturated Log Likelihood
Pattern recognition and Classification
What is Biostatistics?
Evidential Statistics
Statistical Forensic Applications
What Is a Systematic Review?
What Is the Black-Sholes Model?
What Is a Classification Tree?
What Is a Regression Tree?
Cluster Analysis for Correlated Variables
Capture-Recapture Methods
Tchebysheff Inequality and Its Improvements
Frechet Bounds for Dependent Random Variables
Statistical Data Analysis in Criminal Justice
What is Intelligent Numerical Computation?
Software Engineering by Project Management
Chi-Square Analysis for Categorical Grouped Data
Cohen's Kappa: Measures of Data Consistency
Modeling Dependent Categorical Data
The Deming Paradigm
Reliability & Repairable System
Computation of Standard Scores
Quality Function Deployment (QFD)
Event History Analysis
Kinds of Lies: Lies, Damned Lies and Statistics
Factor Analysis
Entropy Measure
Warranties: Statistical Planning and Analysis
Tests for Normality
Directional (i.e., circular) Data Analysis
Introduction
Decision making process under uncertainty is largely based on application of statistical data analysis for probabilistic risk assessment of your decision. Managers need to understand variation for two key reasons. First, so that they can lead others to apply statistical thinking in day to day activities and secondly, to apply the concept for the purpose of continuous improvement. This course will provide you with hands-on experience to promote the use of statistical thinking and techniques to apply them to make educated decisions whenever there is variation in business data. Therefore, it is a course in statistical thinking via a data-oriented approach.
Statistical models are currently used in various fields of business and science. However, the terminology differs from field to field. For example, the fitting of models to data, called calibration, history matching, and data assimilation, are all synonymous with parameter estimation.
Your organization database contains a wealth of information, yet the decision technology group members tap a fraction of it. Employees waste time scouring multiple sources for a database. The decision-makers are frustrated because they cannot get business-critical data exactly when they need it. Therefore, too many decisions are based on guesswork, not facts. Many opportunities are also missed, if they are even noticed at all.
Knowledge is what we know well. Information is the communication of knowledge. In every knowledge exchange, there is a sender and a receiver. The sender make common what is private, does the informing, the communicating. Information can be classified as explicit and tacit forms. The explicit information can be explained in structured form, while tacit information is inconsistent and fuzzy to explain. Know that data are only crude information and not knowledge by themselves.
Data is known to be crude information and not knowledge by itself. The sequence from data to knowledge is: from Data to Information, from Information to Facts, and finally, from Facts to Knowledge. Data becomes information, when it becomes relevant to your decision problem. Information becomes fact, when the data can support it. Facts are what the data reveals. However the decisive instrumental (i.e., applied) knowledge is expressed together with some statistical degree of confidence.
Fact becomes knowledge, when it is used in the successful completion of a decision process. Once you have a massive amount of facts integrated as knowledge, then your mind will be superhuman in the same sense that mankind with writing is superhuman compared to mankind before writing. The following figure illustrates the statistical thinking process based on data in constructing statistical models for decision making under uncertainties.
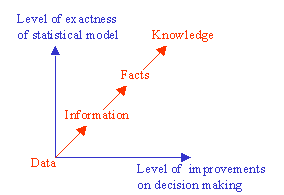
The above figure depicts the fact that as the exactness of a statistical model increases, the level of improvements in decision-making increases. That's why we need statistical data analysis. Statistical data analysis arose from the need to place knowledge on a systematic evidence base. This required a study of the laws of probability, the development of measures of data properties and relationships, and so on.
Statistical inference aims at determining whether any statistical significance can be attached that results after due allowance is made for any random variation as a source of error. Intelligent and critical inferences cannot be made by those who do not understand the purpose, the conditions, and applicability of the various techniques for judging significance.
Considering the uncertain environment, the chance that "good decisions" are made increases with the availability of "good information." The chance that "good information" is available increases with the level of structuring the process of Knowledge Management. The above figure also illustrates the fact that as the exactness of a statistical model increases, the level of improvements in decision-making increases.
Knowledge is more than knowing something technical. Knowledge needs wisdom. Wisdom is the power to put our time and our knowledge to the proper use. Wisdom comes with age and experience. Wisdom is the accurate application of accurate knowledge and its key component is to knowing the limits of your knowledge. Wisdom is about knowing how something technical can be best used to meet the needs of the decision-maker. Wisdom, for example, creates statistical software that is useful, rather than technically brilliant. For example, ever since the Web entered the popular consciousness, observers have noted that it puts information at your fingertips but tends to keep wisdom out of reach.
Almost every professionals need a statistical toolkit. Statistical skills enable you to intelligently collect, analyze and interpret data relevant to their decision-making. Statistical concepts enable us to solve problems in a diversity of contexts. Statistical thinking enables you to add substance to your decisions.
The appearance of computer software, JavaScript Applets, Statistical Demonstrations Applets, and Online Computation are the most important events in the process of teaching and learning concepts in model-based statistical decision making courses. These tools allow you to construct numerical examples to understand the concepts, and to find their significance for yourself.
We will apply the basic concepts and methods of statistics you've already learned in the previous statistics course to the real world problems. The course is tailored to meet your needs in the statistical business-data analysis using widely available commercial statistical computer packages such as SAS and SPSS. By doing this, you will inevitably find yourself asking questions about the data and the method proposed, and you will have the means at your disposal to settle these questions to your own satisfaction. Accordingly, all the applications problems are borrowed from business and economics. By the end of this course you'll be able to think statistically while performing any data analysis.
There are two general views of teaching/learning statistics: Greater and Lesser Statistics. Greater statistics is everything related to learning from data, from the first planning or collection, to the last presentation or report. Lesser statistics is the body of statistical methodology. This is a Greater Statistics course.
There are basically two kinds of "statistics" courses. The real kind shows you how to make sense out of data. These courses would include all the recent developments and all share a deep respect for data and truth. The imitation kind involves plugging numbers into statistics formulas. The emphasis is on doing the arithmetic correctly. These courses generally have no interest in data or truth, and the problems are generally arithmetic exercises. If a certain assumption is needed to justify a procedure, they will simply tell you to "assume the ... are normally distributed" -- no matter how unlikely that might be. It seems like you all are suffering from an overdose of the latter. This course will bring out the joy of statistics in you.
Statistics is a science assisting you to make decisions under uncertainties (based on some numerical and measurable scales). Decision making process must be based on data neither on personal opinion nor on belief.
It is already an accepted fact that "Statistical thinking will one day be as necessary for efficient citizenship as the ability to read and write." So, let us be ahead of our time.
Popular Distributions and Their Typical Applications
Binomial
Application: Gives probability of exactly successes in n independent trials, when probability of success p on single trial is a constant. Used frequently in quality control, reliability, survey sampling, and other industrial problems.Example: What is the probability of 7 or more "heads" in 10 tosses of a fair coin?
Comments: Can sometimes be approximated by normal or by Poisson distribution.
Multinomial
Application: Gives probability of exactly ni outcomes of event i, for i = 1, 2, ..., k in n independent trials when the probability pi of event i in a single trial is a constant. Used frequently in quality control and other industrial problems.Example: Four companies are bidding for each of three contracts, with specified success probabilities. What is the probability that a single company will receive all the orders?
Comments: Generalization of binomial distribution for ore than 2 outcomes.
Hypergeometric
Application: Gives probability of picking exactly x good units in a sample of n units from a population of N units when there are k bad units in the population. Used in quality control and related applications.Example: Given a lot with 21 good units and four defective. What is the probability that a sample of five will yield not more than one defective?
Comments: May be approximated by binomial distribution when n is small related to N.
Geometric
Application: Gives probability of requiring exactly x binomial trials before the first success is achieved. Used in quality control, reliability, and other industrial situations.Example: Determination of probability of requiring exactly five tests firings before first success is achieved.
Pascal
Application: Gives probability of exactly x failures preceding the sth success.Example: What is the probability that the third success takes place on the 10th trial?
Negative Binomial
Application: Gives probability similar to Poisson distribution when events do not occur at a constant rate and occurrence rate is a random variable that follows a gamma distribution.
Example: Distribution of number of cavities for a group of dental patients.
Comments: Generalization of Pascal distribution when s is not an integer. Many authors do not distinguish between Pascal and negative binomial distributions.
Poisson
Application: Gives probability of exactly x independent occurrences during a given period of time if events take place independently and at a constant rate. May also represent number of occurrences over constant areas or volumes. Used frequently in quality control, reliability, queuing theory, and so on.Example: Used to represent distribution of number of defects in a piece of material, customer arrivals, insurance claims, incoming telephone calls, alpha particles emitted, and so on.
Comments: Frequently used as approximation to binomial distribution.
Normal
Application: A basic distribution of statistics. Many applications arise from central limit theorem (average of values of n observations approaches normal distribution, irrespective of form of original distribution under quite general conditions). Consequently, appropriate model for many, but not all, physical phenomena.Example: Distribution of physical measurements on living organisms, intelligence test scores, product dimensions, average temperatures, and so on.
Comments: Many methods of statistical analysis presume normal distribution.
A so-called Generalized Gaussian distribution has the following pdf:
A.exp[-B|x|n], where A, B, n are constants. For n=1 and 2 it is Laplacian and Gaussian distribution respectively. This distribution approximates reasonably good data in some image coding application.
Slash distribution is the distribution of the ratio of a normal random variable to an independent uniform random variable, see Hutchinson T., Continuous Bivariate Distributions, Rumsby Sci. Publications, 1990.
Gamma
Application: A basic distribution of statistics for variables bounded at one side - for example x greater than or equal to zero. Gives distribution of time required for exactly k independent events to occur, assuming events take place at a constant rate. Used frequently in queuing theory, reliability, and other industrial applications.
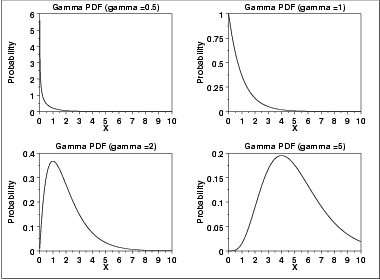
Example: Distribution of time between re calibrations of instrument that needs re calibration after k uses; time between inventory restocking, time to failure for a system with standby components.
Comments: Erlangian, exponential, and chi- square distributions are special cases. The Dirichlet is a multidimensional extension of the Beta distribution.
Distribution of a product of iid uniform (0, 1) random? Like many problems with products, this becomes a familiar problem when turned into a problem about sums. If X is uniform (for simplicity of notation make it U(0,1)), Y=-log(X) is exponentially distributed, so the log of the product of X1, X2, ... Xn is the sum of Y1, Y2, ... Yn which has a gamma (scaled chi-square) distribution. Thus, it is a gamma density with shape parameter n and scale 1.
Exponential
Application: Gives distribution of time between independent events occurring at a constant rate. Equivalently, probability distribution of life, presuming constant conditional failure (or hazard) rate. Consequently, applicable in many, but not all reliability situations.Example: Distribution of time between arrival of particles at a counter. Also life distribution of complex nonredundant systems, and usage life of some components - in particular, when these are exposed to initial burn-in, and preventive maintenance eliminates parts before wear-out.
Comments: Special case of both Weibull and gamma distributions.
Beta

Application: A basic distribution of statistics for variables bounded at both sides - for example x between o and 1. Useful for both theoretical and applied problems in many areas.
Example: Distribution of proportion of population located between lowest and highest value in sample; distribution of daily per cent yield in a manufacturing process; description of elapsed times to task completion (PERT).
Comments: Uniform, right triangular, and parabolic distributions are special cases. To generate beta, generate two random values from a gamma, g1, g2. The ratio g1/(g1 +g2) is distributed like a beta distribution. The beta distribution can also be thought of as the distribution of X1 given (X1+X2), when X1 and X2 are independent gamma random variables.
There is also a relationship between the Beta and Normal distributions. The conventional calculation is that given a PERT Beta with highest value as b lowest as a and most likely as m, the equivalent normal distribution has a mean and mode of (a + 4M + b)/6 and a standard deviation of (b - a)/6.
See Section 4.2 of, Introduction to Probability by J. Laurie Snell (New York, Random House, 1987) for a link between beta and F distributions (with the advantage that tables are easy to find).
Uniform
Application: Gives probability that observation will occur within a particular interval when probability of occurrence within that interval is directly proportional to interval length.Example: Used to generate random valued.
Comments: Special case of beta distribution.
The density of geometric mean of n independent uniforms(0,1) is:
P(X=x) = n x(n-1) (Log[1/xn])(n-1) / (n-1)!.
zL = [UL-(1-U)L]/L is said to have Tukey's symmetrical l-distribution.
Log-normal
Application: Permits representation of random variable whose logarithm follows normal distribution. Model for a process arising from many small multiplicative errors. Appropriate when the value of an observed variable is a random proportion of the previously observed value.In the case where the data are lognormally distributed, the geometric mean acts as a better data descriptor than the mean. The more closely the data follow a lognormal distribution, the closer the geometric mean is to the median, since the log re-expression produces a symmetrical distribution.
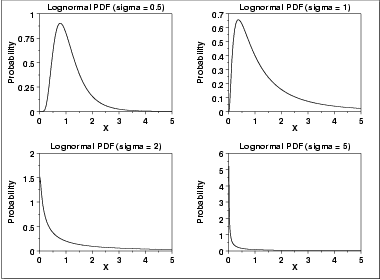
Example: Distribution of sizes from a breakage process; distribution of income size, inheritances and bank deposits; distribution of various biological phenomena; life distribution of some transistor types.
The ratio of two log-normally distributed variables is
log-normal.
Rayleigh
Application: Gives distribution of radial error when the errors in two mutually perpendicular axes are independent and normally distributed around zero with equal variances.Example: Bomb-sighting problems; amplitude of noise envelope when a linear detector is used.
Comments: Special case of Weibull distribution.
Cauchy
Application: Gives distribution of ratio of two independent standardized normal variates.Example: Distribution of ratio of standardized noise readings; distribution of tan(x) when x is uniformly distributed.
Chi-square
The probability density curve of a chi-square distribution is asymmetric curve stretching over the positive side of the line and having a long right tail. The form of the curve depends on the value of the degrees of freedom.Applications: The most widely applications of Chi-square distribution are:
- Chi-square Test for Association is a (non-parametric, therefore can be used for nominal data) test of statistical significance widely used bivariate tabular association analysis. Typically, the hypothesis is whether or not two different populations are different enough in some characteristic or aspect of their behavior based on two random samples. This test procedure is also known as the Pearson chi-square test.
- Chi-square Goodness-of-fit Test is used to test if an observed distribution conforms to any particular distribution. Calculation of this goodness of fit test is by comparison of observed data with data expected based on the particular distribution.
Weibull
Application: General time-to-failure distribution due to wide diversity of hazard-rate curves, and extreme-value distribution for minimum of N values from distribution bounded at left.The Weibull distribution is often used to model "time until failure." In this manner, it is applied in actuarial science and in engineering work.
It is also an appropriate distribution for describing data corresponding to resonance behavior, such as the variation with energy of the cross section of a nuclear reaction or the variation with velocity of the absorption of radiation in the Mossbauer effect.
Example: Life distribution for some capacitors, ball bearings, relays, and so on.
Comments: Rayleigh and exponential distribution are special cases.
Extreme value
Application: Limiting model for the distribution of the maximum or minimum of N values selected from an "exponential-type" distribution, such as the normal, gamma, or exponential.Example: Distribution of breaking strength of some materials, capacitor breakdown voltage, gust velocities encountered by airplanes, bacteria extinction times.
t distributions
The t distributions were discovered in 1908 by William Gosset who was a chemist and a statistician employed by the Guinness brewing company. He considered himself a student still learning statistics, so that is how he signed his papers as pseudonym "Student". Or perhaps he used a pseudonym due to "trade secrets" restrictions by Guinness.Note that there are different t distributions, it is a class of distributions. When we speak of a specific t distribution, we have to specify the degrees of freedom. The t density curves are symmetric and bell-shaped like the normal distribution and have their peak at 0. However, the spread is more than that of the standard normal distribution. The larger the degrees of freedom, the closer the t-density is to the normal density.
Why Is Every Thing Priced One Penny Off the Dollar?
Here's a psychological answer. Due to a very limited data processing ability we humans rely heavily on categorization (e.g., seeing things as "black or white" requires just a binary coding scheme, as opposed to seeing the many shades of gray). Our number system has a major category of 100's (e.g., 100 pennies, 200 pennies, 300 pennies) and there is a affective response associated with these groups--more is better if you are getting them; more is bad if you are giving them. Advertising and pricing takes advantage of this limited data processing by $2.99, $3.95, etc. So that $2.99 carries the affective response associated with the 200 pennies group. Indeed, if you ask people to respond to "how close together" are 271 & 283 versus "how close together" are 291 & 303, the former are seen as closer (there's a lot of methodology set up to dissuade the subjects to just subtract the smaller from the larger). Similarly, prejudice, job promotions, competitive sports, and a host of other activates attempt to associate large qualitative differences with what are often minor quantitative differences, e.g., gold metal in Olympic swimming event may be milliseconds difference from no metal.Yet another motivation: Psychologically $9.99 might look better than $10.00, but there is a more basic reason too. The assistant has to give you change from your ten dollars, and has to ring the sale up through his/her cash register to get at the one cent. This forces the transaction to go through the books, you get a receipt, and the assistant can't just pocket the $10 him/herself. Mind you, there's nothing to stop a particularly untrustworthy employee going into work with a pocketful of cents...
There's sales tax for that. For either price (at least in the US), you'll have to pay sales tax too. So that solves the problem of opening the cash register. That, plus the security cameras ;).
There has been some research in marketing theory on the consumer's behavior at particular price points. Essentially, these are tied up with buyer expectations based on prior experience. A critical case study in UK on price pointing of pantyhose (tights) shown that there were distinct demand peaks at buyer anticipated price points of 59p, 79p, 99p, £1.29 and so on. Demand at intermediate price points was dramatically below these anticipated points for similar quality goods. In the UK, for example, prices of wine are usually set at key price points. The wine retailers also confirm that sales at different prices (even a penny or so different) does result in dramatically different sales volumes.
Other studies showed the opposite where reduced price showed reduced sales volumes, consumers ascribing quality in line with price. However, it is not fully tested to determine if sales volume continued to increase with price.
Other similar research turns on the behavior of consumers to variations in price. The key issue here is that there is a Just Noticeable Difference (JND) below which consumers will not act on a price increase. This has practical application when increasing charge rates and the like. The JND is typically 5% and this provides the opportunity for consultants etc to increase prices above prior rates by less than the JND without customer complaint. As an empirical experiment, try overcharging clients by 1, 2,.., 5, 6% and watch the reaction. Up to 5% there appears to be no negative impact.
Conversely, there is no point in offering a fee reduction of less than 5% as clients will not recognize the concession you have made. Equally, in periods of price inflation, price rises should be staged so that the individual price rise is kept under 5%, perhaps by raising prices by 4% twice per year rather than a one off 8% rise.
A Short History of Probability and Statistics
The original idea of "statistics" was the collection of information about and for the "state". The word statistics drives directly not from any classical Greek or Latin roots, but from the Italian word for state.The birth of statistics occurred in mid-17th century. A commoner, named John Graunt, who was a native of London, begin reviewing a weekly church publication issued by the local parish clerk that listed the number of births, christenings, and deaths in each parish. These so called Bills of Mortality also listed the causes of death. Graunt who was a shopkeeper organized this data in the forms we call descriptive statistics, which was published as Natural and Political Observation Made upon the Bills of Mortality. Shortly thereafter, he was elected as a member of Royal Society. Thus, statistics has to borrow some concepts from sociology, such as the concept of "Population". It has been argued that since statistics usually involves the study of human behavior, it cannot claim the precision of the physical sciences.
Probability has much longer history. Probability is derived from the verb to probe meaning to "find out" what is not too easily accessible or understandable. The word "proof" has the same origin that provides necessary details to understand what is claimed to be true.
Probability originated from the study of games of chance and gambling during the sixteenth century. Probability theory was a branch of mathematics studied by Blaise Pascal and Pierre de Fermat in the seventeenth century. Currently; in 21st century, probabilistic modeling are used to control the flow of traffic through a highway system, a telephone interchange, or a computer processor; find the genetic makeup of individuals or populations; quality control; insurance; investment; and other sectors of business and industry.
New and ever growing diverse fields of human activities are using statistics; however, it seems that this field itself remains obscure to the public. Professor Bradley Efron expressed this fact nicely:
Further Readings:
Daston L., Classical Probability in the Enlightenment, Princeton University Press, 1988.
The book points out that early Enlightenment thinkers could not face uncertainty. A mechanistic, deterministic machine, was the Enlightenment view of the world.
Gillies D., Philosophical Theories of Probability, Routledge, 2000. Covers the classical, logical, subjective, frequency, and propensity views.
Hacking I., The Emergence of Probability, Cambridge University Press, London, 1975. A philosophical study of early ideas about probability, induction and statistical inference.
Peters W., Counting for Something: Statistical Principles and Personalities, Springer, New York, 1987. It teaches the principles of applied economic and social statistics in a historical context. Featured topics include public opinion polls, industrial quality control, factor analysis, Bayesian methods, program evaluation, non-parametric and robust methods, and exploratory data analysis.
Porter T., The Rise of Statistical Thinking, 1820-1900, Princeton University Press, 1986.
The author states that statistics has become known in the twentieth century as the mathematical tool for analyzing experimental and observational data. Enshrined by public policy as the only reliable basis for judgments as the efficacy of medical procedures or the safety of chemicals, and adopted by business for such uses as industrial quality control, it is evidently among the products of science whose influence on public and private life has been most pervasive. Statistical analysis has also come to be seen in many scientific disciplines as indispensable for drawing reliable conclusions from empirical results.This new field of mathematics found so extensive a domain of applications.
Stigler S., The History of Statistics: The Measurement of Uncertainty Before 1900, U. of Chicago Press, 1990. It covers the people, ideas, and events underlying the birth and development of early statistics.
Tankard J., The Statistical Pioneers, Schenkman Books, New York, 1984.
This work provides the detailed lives and times of theorists whose work continues to shape much of the modern statistics.
Different Schools of Thought in Statistics
There are few different schools of thoughts in statistics. They are introduced sequentially in time by necessity.The Birth Process of a New School of Thought
The process of devising a new school of thought in any field has always taken a natural path. Birth of new schools of thought in statistics is not an exception. The birth process is outlined below:
Given an already established school, one must work within the defined framework.
A crisis appears, i.e., some inconsistencies in the framework result from its own laws.
Response behavior:
- Reluctance to consider the crisis.
- Try to accommodate and explain the crisis within the existing framework.
- Conversion of some well-known scientists attracts followers in the new school.
The perception of a crisis in statistical community calls forth demands for "foundation-strengthens". After the crisis is over, things may look different and historians of statistics may cast the event as one in a series of steps in "building upon a foundation". So we can read histories of statistics, as the story of a pyramid built up layer by layer on a firm base over time.
Other schools of thought are emerging to extend and "soften" the existing theory of probability and statistics. Some "softening" approaches utilize the concepts and techniques developed in the fuzzy set theory, the theory of possibility, and Dempster-Shafer theory.
The following Figure illustrates the three major schools of thought; namely, the Classical (attributed to Laplace), Relative Frequency (attributed to Fisher), and Bayesian (attributed to Savage). The arrows in this figure represent some of the main criticisms among Objective, Frequentist, and Subjective schools of thought. To which school do you belong? Read the conclusion in this figure.
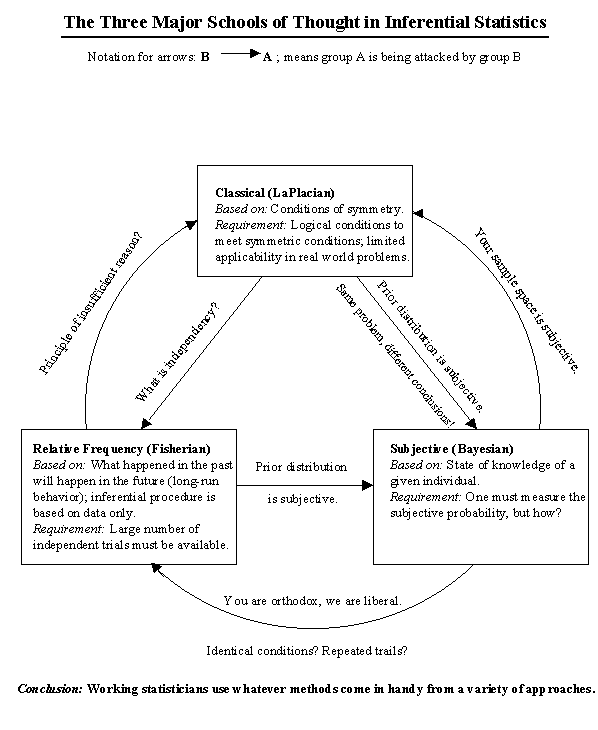
What Type of Statistician Are You?
Click on the image to enlarge it
Further Readings:
Plato, Jan von, Creating Modern Probability, Cambridge University Press, 1994. This book provides a historical point of view on subjectivist and objectivist probability school of thoughts.
Press S., and J. Tanur, The Subjectivity
of Scientists and the Bayesian Approach, Wiley, 2001. Comparing and contrasting the reality of subjectivity in the work of history's great scientists and the modern Bayesian approach to statistical analysis.
Weatherson B., Begging the question and Bayesians, Studies in History and Philosophy of Science, 30(4), 687-697, 1999.
Bayesian, Frequentist, and Classical Methods
The problem with the Classical Approach is that what constitutes an outcome is not objectively determined. One person's simple event is another person's compound event. One researcher may ask, of a newly discovered planet, "what is the probability that life exists on the new planet?" while another may ask "what is the probability that carbon-based life exists on it?"Bruno de Finetti, in the introduction to his two-volume treatise on Bayesian ideas, clearly states that "Probabilities Do not Exist". By this he means that probabilities are not located in coins or dice; they are not characteristics of things like mass, density, etc.
Some Bayesian approaches consider probability theory as an extension of deductive logic (including dialogue logic, interrogative logic, informal logic, and artificial intelligence) to handle uncertainty. It purports to deduce from first principles the uniquely correct way of representing your beliefs about the state of things, and updating them in the light of the evidence. The laws of probability have the same status as the laws of logic. These Bayesian approaches are explicitly "subjective" in the sense that they deal with the plausibility which a rational agent ought to attach to the propositions he/she considers, "given his/her current state of knowledge and experience." By contrast, at least some non-Bayesian approaches consider probabilities as "objective" attributes of things (or situations) which are really out there (availability of data).
A Bayesian and a classical statistician analyzing the same data will generally reach the same conclusion. However, the Bayesian is better able to quantify the true uncertainty in his analysis, particularly when substantial prior information is available. Bayesians are willing to assign probability distribution function(s) to the population's parameter(s) while frequentists are not.
From a scientist's perspective, there are good grounds to reject Bayesian reasoning. The problem is that Bayesian reasoning deals not with objective, but subjective probabilities. The result is that any reasoning using a Bayesian approach cannot be publicly checked -- something that makes it, in effect, worthless to science, like non replicative experiments.
Bayesian perspectives often shed a helpful light on classical procedures. It is necessary to go into a Bayesian framework to give confidence intervals the probabilistic interpretation which practitioners often want to place on them. This insight is helpful in drawing attention to the point that another prior distribution would lead to a different interval.
A Bayesian may cheat by basing the prior distribution on the data; a Frequentist can base the hypothesis to be tested on the data. For example, the role of a protocol in clinical trials is to prevent this from happening by requiring the hypothesis to be specified before the data are collected. In the same way, a Bayesian could be obliged to specify the prior in a public protocol before beginning a study. In a collective scientific study, this would be somewhat more complex than for Frequentist hypotheses because priors must be personal for coherence to hold.
A suitable quantity that has been proposed to measure inferential uncertainty; i.e., to handle the a priori unexpected, is the likelihood function itself.
If you perform a series of identical random experiments (e.g., coin tosses), the underlying probability distribution that maximizes the probability of the outcome you observed is the probability distribution proportional to the results of the experiment.
This has the direct interpretation of telling how (relatively) well each possible explanation (model), whether obtained from the data or not, predicts the observed data. If the data happen to be extreme ("atypical") in some way, so that the likelihood points to a poor set of models, this will soon be picked up in the next rounds of scientific investigation by the scientific community. No long run frequency guarantee nor personal opinions are required.
There is a sense in which the Bayesian approach is oriented toward making decisions and the frequentist hypothesis testing approach is oriented toward science. For example, there may not be enough evidence to show scientifically that agent X is harmful to human beings, but one may be justified in deciding to avoid it in one's diet.
In almost all cases, a point estimate is a continuous random variable. Therefore, the probability that the probability is any specific point estimate is really zero. This means that in a vacuum of information, we can make no guess about the probability. Even if we have information, we can really only guess at a range for the probability.
Therefore, in estimating a parameter of a given population, it is necessary that a point estimate accompanied by some measure of possible error of the estimate. The widely acceptable approach is that a point estimate must be accompanied by some interval about the estimate with some measure of assurance that this interval contains the true value of the population parameter. For example, the reliability assurance processes in manufacturing industries are based on data driven information for making product-design decisions.
Objective Bayesian: There is a clear connection between probability and logic: both appear to tell us how we should reason. But how, exactly, are the two concepts related? Objective Bayesians offers one answer to this question. According to objective Bayesians, probability generalizes deductive logic: deductive logic tells us which conclusions are certain, given a set of premises, while probability tells us the extent to which one should believe a conclusion, given the premises certain conclusions being awarded full degree of belief. According to objective Bayesians, the premises objectively (i.e. uniquely) determine the degree to which one should believe a conclusion.
Further Readings:
Bernardo J., and A. Smith, Bayesian Theory, Wiley, 2000.
Congdon P., Bayesian Statistical Modelling, Wiley, 2001.
Corfield D., and J. Williamson, Foundations of Bayesianism, Kluwer Academic Publishers, 2001. Contains
Logic, Mathematics, Decision Theory, and Criticisms of Bayesianism.
Land F., Operational Subjective Statistical Methods, Wiley, 1996. Presents a systematic treatment of subjectivist methods along with a good discussion of the historical and philosophical backgrounds of the major approaches to probability and statistics.
Press S., Subjective and Objective Bayesian Statistics: Principles, Models, and Applications, Wiley, 2002.
Zimmerman H., Fuzzy Set Theory, Kluwer Academic Publishers, 1991. Fuzzy logic approaches to probability (based on L.A. Zadeh and his followers) present a difference between "possibility
theory" and probability theory.
Rumor, Belief, Opinion, and Fact
As a necessity the human rational strategic thinking has evolved to cope with his/her environment. The rational strategic thinking which we call reasoning is another means to make the world calculable, predictable, and more manageable for the utilitarian purposes. In constructing a model of reality, factual information is therefore needed to initiate any rational strategic thinking in the form of reasoning. However, we should not confuse facts with beliefs, opinions, or rumors. The following table helps to clarify the distinctions:
Rumor
Belief
Opinion
Fact
One says to oneself
I need to use it anyway
This is the truth. I'm right
This is my view
This is a fact
One says to others
It could be true. You know!
You're wrong
That is yours
I can explain it to you
Beliefs are defined as someone's own understanding. In belief, "I am" always right and "you" are wrong. There is nothing that can be done to convince the person that what they believe is wrong.
With respect to belief, Henri Poincaré said, "Doubt everything or believe everything: these are two equally convenient strategies. With either, we dispense with the need to think." Believing means not wanting to know what is fact. Human beings are most apt to believe what they least understand. Therefore, you may rather have a mind opened by wonder than one closed by belief. The greatest derangement of the mind is to believe in something because one wishes it to be so.
The history of mankind is filled with unsettling normative perspectives reflected in, for example, inquisitions, witch hunts, denunciations, and brainwashing techniques. The "sacred beliefs" are not only within religion, but also within ideologies, and could even include science. In much the same way many scientists trying to "save the theory." For example, the Freudian treatment is a kind of brainwashing by the therapist where the patient is in a suggestive mood completely and religiously believing in whatever the therapist is making of him/her and blaming himself/herself in all cases. There is this huge lumbering momentum from the Cold War where thinking is still not appreciated. Nothing is so firmly believed as that which is least known.
The history of humanity is also littered with discarded belief-models. However, this does not mean that someone who didn't understand what was going on invented the model nor had no utility or practical value. The main idea was the cultural values of any wrong model. The falseness of a belief is not necessarily an objection to a belief. The question is, to what extent is it life-promoting, and life enhancing for the believer?
Opinions (or feelings) are slightly less extreme than beliefs however, they are dogmatic. An opinion means that a person has certain views that they think are right. Also, they know that others are entitled to their own opinions. People respect others' opinions and in turn expect the same. In forming one's opinion, the empirical observations are obviously strongly affected by attitude and perception. However, opinions that are well rooted should grow and change like a healthy tree. Fact is the only instructional material that can be presented in an entirely non-dogmatic way. Everyone has a right to his/her own opinion, but no one has a right to be wrong in his/her facts.
Public opinion is often a sort of religion, with the majority as its prophet. Moreover, the profit has a short memory and does not provide consistent opinions over time.
Rumors and gossip are even weaker than opinion. Now the question is who will believe these? For example, rumors and gossip about a person are those when you hear something you like, about someone you do not. Here is an example you might be familiar with: Why is there no Nobel Prize for mathematics? It is the opinion of many that Alfred Nobel caught his wife in an amorous situation with Mittag-Leffler, the foremost Swedish mathematician at the time. Therefore, Nobel was afraid that if he were to establish a mathematics prize, the first to get it would be M-L. The story persists, no matter how often one repeats the plain fact that Nobel was not married.
To understand the difference between feeling and strategic thinking , consider carefully the following true statement: He that thinks himself the happiest man really is so; but he that thinks himself the wisest is generally the greatest fool. Most people do not ask for facts in making up their decisions. They would rather have one good, soul-satisfying emotion than a dozen facts. This does not mean that you should not feel anything. Notice your feelings. But do not think with them.
Facts are different than beliefs, rumors, and opinions. Facts are the basis of decisions. A fact is something that is right and one can prove to be true based on evidence and logical arguments. A fact can be used to convince yourself, your friends, and your enemies. Facts are always subject to change. Data becomes information when it becomes relevant to your decision problem. Information becomes fact when the data can support it. Fact becomes knowledge when it is used in the successful completion of a structured decision process. However, a fact becomes an opinion if it allows for different interpretations, i.e., different perspectives. Note that what happened in the past is fact, not truth. Truth is what we think about, what happened (i.e., a model).
Business Statistics is built up with facts, as a house is with stones. But a collection of facts is no more a useful and instrumental science for the manager than a heap of stones is a house.
Science and religion are profoundly different. Religion asks us to believe without question, even (or especially) in the absence of hard evidence. Indeed, this is essential for having a faith. Science asks us to take nothing on faith, to be wary of our penchant for self-deception, to reject anecdotal evidence. Science considers deep but healthy skepticism a prime feature. One of the reasons for its success is that science has built-in, error-correcting machinery at its very heart.
Learn how to approach information critically and discriminate in a principled way between beliefs, opinions, and facts. Critical thinking is needed to produce well-reasoned representation of reality in your modeling process. Analytical thinking demands clarity, consistency, evidence, and above all, a consecutive, focused-thinking.
Further Readings:
Boudon R., The Origin of Values: Sociology and Philosophy of Belief, Transaction Publishers, London, 2001.
Castaneda C., The Active Side of Infinity, Harperperennial Library, 2000.
Goodwin P., and G. Wright,
Decision Analysis for Management Judgment, Wiley, 1998.
Jurjevich R., The Hoax of Freudism: A Study of Brainwashing the American Professionals and Laymen, Philadelphia, Dorrance, 1974.
Kaufmann W., Religions in Four Dimensions: Existential and Aesthetic, Historical and
Comparative, Reader's Digest Press, 1976.
What is Statistical Data Analysis? Data are not Information!
Data are not information! To determine what statistical data analysis is, one must first define statistics. Statistics is a set of methods that are used to collect, analyze, present, and interpret data. Statistical methods are used in a wide variety of occupations and help people identify, study, and solve many complex problems. In the business and economic world, these methods enable decision makers and managers to make informed and better decisions about uncertain situations.Vast amounts of statistical information are available in today's global and economic environment because of continual improvements in computer technology. To compete successfully globally, managers and decision makers must be able to understand the information and use it effectively. Statistical data analysis provides hands on experience to promote the use of statistical thinking and techniques to apply in order to make educated decisions in the business world.
Computers play a very important role in statistical data analysis. The statistical software package, SPSS, which is used in this course, offers extensive data-handling capabilities and numerous statistical analysis routines that can analyze small to very large data statistics. The computer will assist in the summarization of data, but statistical data analysis focuses on the interpretation of the output to make inferences and predictions.
Studying a problem through the use of statistical data analysis usually involves four basic steps.
1. Defining the problem
2. Collecting the data
3. Analyzing the data
4. Reporting the results
Defining the Problem
An exact definition of the problem is imperative in order to obtain accurate data about it. It is extremely difficult to gather data without a clear definition of the problem.
Collecting the Data
Designing ways to collect data is an important job in statistical data analysis. Two important aspects of a statistical study are:
Population - a set of all the elements of interest in a study
Sample - a subset of the population
Statistical inference is refer to extending your knowledge obtain from a random sample from a population to the whole population. This is known in mathematics as an Inductive Reasoning. That is, knowledge of whole from a particular. Its main application is in hypotheses testing about a given population.
The purpose of statistical inference is to obtain information about a population form information contained in a sample. It is just not feasible to test the entire population, so a sample is the only realistic way to obtain data because of the time and cost constraints. Data can be either quantitative or qualitative. Qualitative data are labels or names used to identify an attribute of each element. Quantitative data are always numeric and indicate either how much or how many.
For the purpose of statistical data analysis, distinguishing between cross-sectional and time series data is important. Cross-sectional data re data collected at the same or approximately the same point in time. Time series data are data collected over several time periods.
Data can be collected from existing sources or obtained through observation and experimental studies designed to obtain new data. In an experimental study, the variable of interest is identified. Then one or more factors in the study are controlled so that data can be obtained about how the factors influence the variables. In observational studies, no attempt is made to control or influence the variables of interest. A survey is perhaps the most common type of observational study.
Analyzing the Data
Statistical data analysis divides the methods for analyzing data into two categories: exploratory methods and confirmatory methods. Exploratory methods are used to discover what the data seems to be saying by using simple arithmetic and easy-to-draw pictures to summarize data. Confirmatory methods use ideas from probability theory in the attempt to answer specific questions. Probability is important in decision making because it provides a mechanism for measuring, expressing, and analyzing the uncertainties associated with future events. The majority of the topics addressed in this course fall under this heading.
Reporting the Results
Through inferences, an estimate or test claims about the characteristics of a population can be obtained from a sample. The results may be reported in the form of a table, a graph or a set of percentages. Because only a small collection (sample) has been examined and not an entire population, the reported results must reflect the uncertainty through the use of probability statements and intervals of values.
To conclude, a critical aspect of managing any organization is planning for the future. Good judgment, intuition, and an awareness of the state of the economy may give a manager a rough idea or "feeling" of what is likely to happen in the future. However, converting that feeling into a number that can be used effectively is difficult. Statistical data analysis helps managers forecast and predict future aspects of a business operation. The most successful managers and decision makers are the ones who can understand the information and use it effectively.
visit also Different Approaches to Statistical Thinking
Data Processing: Coding, Typing, and Editing
Data are often recorded manually on data sheets. Unless the numbers of observations and variables are small the data must be analyzed on a computer. The data will then go through three stages:Coding: the data are transferred, if necessary to coded sheets.
Typing: the data are typed and stored by at least two independent data entry persons. For example, when the Current Population Survey and other monthly surveys were taken using paper questionnaires, the U.S. Census Bureau used double key data entry.
Editing: the data are checked by comparing the two independent typed data. The standard practice for key-entering data from paper questionnaires is to key in all the data twice. Ideally, the second time should be done by a different key entry operator whose job specifically includes verifying mismatches between the original and second entries. It is believed that this "double-key/verification" method produces a 99.8% accuracy rate for total keystrokes.
Types of error: Recording error, typing error, transcription error (incorrect copying), Inversion (e.g., 123.45 is typed as 123.54), Repetition (when a number is repeated), Deliberate error.
Type of Data and Levels of Measurement
Information can be collected in statistics using qualitative or quantitative data.Qualitative data, such as eye color of a group of individuals, is not computable by arithmetic relations. They are labels that advise in which category or class an individual, object, or process fall. They are called categorical variables.
Quantitative data sets consist of measures that take numerical values for which descriptions such as means and standard deviations are meaningful. They can be put into an order and further divided into two groups: discrete data or continuous data. Discrete data are countable data, for example, the number of defective items produced during a day's production. Continuous data, when the parameters (variables) are measurable, are expressed on a continuous scale. For example, measuring the height of a person.
The first activity in statistics is to measure or count. Measurement/counting theory is concerned with the connection between data and reality. A set of data is a representation (i.e., a model) of the reality based on a numerical and mensurable scales. Data are called "primary type" data if the analyst has been involved in collecting the data relevant to his/her investigation. Otherwise, it is called "secondary type" data.
Data come in the forms of Nominal, Ordinal, Interval and Ratio (remember the French word NOIR for color black). Data can be either continuous or discrete.
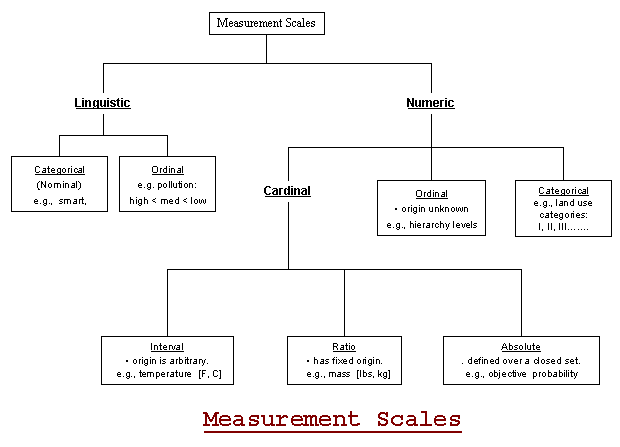
Both zero and unit of measurements are arbitrary in the Interval scale. While the unit of measurement is arbitrary in Ratio scale, its zero point is a natural attribute. The categorical variable is measured on an ordinal or nominal scale.
Measurement theory is concerned with the connection between data and reality. Both statistical theory and measurement theory are necessary to make inferences about reality.
Since statisticians live for precision, they prefer Interval/Ratio levels of measurement.
Problems with Stepwise Variable Selection
Here are some of the common problems with stepwise variable selection in regression analysis.
- It yields R-squared values that are badly biased high.
- The F and chi-squared tests quoted next to each variable on the printout do not have the claimed distribution.
- The method yields confidence intervals for effects and predicted values that are falsely narrow.
- It yields P-values that do not have the proper meaning and the proper correction for them is a very difficult problem
- It gives biased regression coefficients that need shrinkage, i.e., the coefficients for remaining variables are too large.
- It has severe problems in the presence of collinearity.
- It is based on methods (e.g. F-tests for nested models) that were intended to be used to test pre-specified hypotheses.
- Increasing the sample size does not help very much.
Note also that the all-possible-subsets approach does not remove any of the above problems.
Further Reading:
Derksen, S. and H. Keselman, Backward, forward and stepwise automated subset selection algorithms, British Journal of Mathematical and Statistical Psychology, 45, 265-282, 1992.
An Alternative Approach for Estimating a Regression Line
The following approach is the so-called "distribution-free method" for estimating parameters in a simple regression y = mx + b:- Rewrite y = mx + b as b = -xm + y.
- Every data point (xi, yi) corresponds to a line b = -xi m + yi in the Cartesian coordinates plane (m, b), and an estimate of m and b can be obtained from the intersection of pairs of such lines. There are at most n(n+1)/2 such estimates.
- Take the medians to get the final estimates.
Further Readings:
Cornish-Bowden A., Analysis of Enzyme Kinetic Data, Oxford Univ Press, 1995.
Hald A., A History of Mathematical Statistics: From 1750 to 1930, Wiley, New York, 1998. Among others, the author points out that in the beginning of 18-th Century researches had four different methods to solve fitting problems: The Mayer-Laplace method of averages, The Boscovich-Laplace method of least absolute deviations, Laplace method of minimizing the largest absolute residual and the Legendre method of minimizing the sum of squared residuals. The only single way of choosing between these methods was: to compare results of estimates and residuals.
Multivariate Data Analysis
Data are easy to collect; what we really need in complex problem solving is information. We may view a data base as a domain that requires probes and tools to extract relevant information. As in the measurement process itself, appropriate instruments of reasoning must be applied to the data interpretation task. Effective tools serve in two capacities: to summarize the data and to assist in interpretation. The objectives of interpretive aids are to reveal the data at several levels of detail.Exploring the fuzzy data picture sometimes requires a wide-angle lens to view its totality. At other times it requires a closeup lens to focus on fine detail. The graphically based tools that we use provide this flexibility. Most chemical systems are complex because they involve many variables and there are many interactions among the variables. Therefore, chemometric techniques rely upon multivariate statistical and mathematical tools to uncover interactions and reduce the dimensionality of the data.
Multivariate analysis is a branch of statistics involving the consideration of objects on each of which are observed the values of a number of variables. Multivariate techniques are used across the whole range of fields of statistical application: in medicine, physical and biological sciences, economics and social science, and of course in many industrial and commercial applications.
Principal component analysis used for exploring data to reduce the dimension. Generally, PCA seeks to represent n correlated random variables by a reduced set of uncorrelated variables, which are obtained by transformation of the original set onto an appropriate subspace. The uncorrelated variables are chosen to be good linear combination of the original variables, in terms of explaining maximal variance, orthogonal directions in the data. Two closely related techniques, principal component analysis and factor analysis, are used to reduce the dimensionality of multivariate data. In these techniques correlations and interactions among the variables are summarized in terms of a small number of underlying factors. The methods rapidly identify key variables or groups of variables that control the system under study. The resulting dimension reduction also permits graphical representation of the data so that significant relationships among observations or samples can be identified.
Other techniques include Multidimensional Scaling, Cluster Analysis, and Correspondence Analysis.
Further Readings:
Chatfield C., and A. Collins, Introduction to Multivariate Analysis, Chapman and Hall, 1980.
Hoyle R., Statistical Strategies for small Sample Research, Thousand Oaks, CA, Sage, 1999.
Krzanowski W., Principles of Multivariate Analysis: A User's Perspective, Clarendon Press, 1988.
Mardia K., J. Kent and J. Bibby, Multivariate Analysis, Academic Press, 1979.
The Meaning and Interpretation of P-values (what the data say?)
The P-value, which directly depends on a given sample, attempts to provide a measure of the strength of the results of a test, in contrast to a simple reject or do not reject. If the null hypothesis is true and the chance of random variation is the only reason for sample differences, then the P-value is a quantitative measure to feed into the decision making process as evidence. The following table provides a reasonable interpretation of P-values:
| P< 0.01 | very strong evidence against H0 |
| 0.01£ P < 0.05 | moderate evidence against H0 |
| 0.05£ P < 0.10 | suggestive evidence against H0 |
| 0.10£ P | little or no real evidence against H0 |
This interpretation is widely accepted, and many scientific journals routinely publish papers using this interpretation for the result of test of hypothesis.
For the fixed-sample size, when the number of realizations is decided in advance, the distribution of p is uniform (assuming the null hypothesis). We would express this as P(p £ x) = x. That means the criterion of p <0.05 achieves a of 0.05.
When a p-value is associated with a set of data, it is a measure of the probability that the data could have arisen as a random sample from some population described by the statistical (testing) model.
A p-value is a measure of how much evidence you have against the null hypothesis. The smaller the p-value, the more evidence you have. One may combine the p-value with the significance level to make decision on a given test of hypothesis. In such a case, if the p-value is less than some threshold (usually .05, sometimes a bit larger like 0.1 or a bit smaller like .01) then you reject the null hypothesis.
Understand that the distribution of p-values under null hypothesis H0 is uniform, and thus does not depend on a particular form of the statistical test. In a statistical hypothesis test, the P value is the probability of observing a test statistic at least as extreme as the value actually observed, assuming that the null hypothesis is true. The value of p is defined with respect to a distribution. Therefore, we could call it "model-distributional hypothesis" rather than "the null hypothesis".
In short, it simply means that if the null had been true, the p value is the probability against the null in that case. The p-value is determined by the observed value, however, this makes it difficult to even state the inverse of p.
You may like using The P-values for the Popular Distributions Java applet.
Further Readings:
Arsham H., Kuiper's P-value as a Measuring Tool and Decision Procedure for the Goodness-of-fit Test, Journal of Applied Statistics, Vol. 15, No.3, 131-135, 1988.
Accuracy, Precision, Robustness, and Quality
Accuracy refers to the closeness of the measurements to the "actual" or "real" value of the physical quantity, whereas the term precision is used to indicate the closeness with which the measurements agree with one another quite independently of any systematic error involved. Therefore, an "accurate" estimate has small bias. A "precise" estimate has both small bias and variance. Quality is proportion to the inverse of variance.The robustness of a procedure is the extent to which its properties do not depend on those assumptions which you do not wish to make. This is a modification of Box's original version, and this includes Bayesian considerations, loss as well as prior. The central limit theorem (CLT) and the Gauss-Markov Theorem qualify as robustness theorems, but the Huber-Hempel definition does not qualify as a robustness theorem.
We must always distinguish between bias robustness and efficiency robustness. It seems obvious to me that no statistical procedure can be robust in all senses. One needs to be more specific about what the procedure must be protected against. If the sample mean is sometimes seen as a robust estimator, it is because the CLT guarantees a 0 bias for large samples regardless of the underlying distribution. This estimator is bias robust, but it is clearly not efficiency robust as its variance can increase endlessly. That variance can even be infinite if the underlying distribution is Cauchy or Pareto with a large scale parameter. This is the reason for which the sample mean lacks robustness according to Huber-Hampel definition. The problem is that the M-estimator advocated by Huber, Hampel and a couple of other folks is bias robust only if the underlying distribution is symmetric.
In the context of survey sampling, two types of statistical inferences are available: the model-based inference and the design-based inference which exploits only the randomization entailed by the sampling process (no assumption needed about the model). Unbiased design-based estimators are usually referred to as robust estimators because the unbiasedness is true for all possible distributions. It seems clear however, that these estimators can still be of poor quality as the variance that can be unduly large.
However, others people will use the word in other (imprecise) ways. Kendall's Vol. 2, Advanced Theory of Statistics, also cites Box, 1953; and he makes a less useful statement about assumptions. In addition, Kendall states in one place that robustness means (merely) that the test size, a, remains constant under different conditions. This is what people are using, apparently, when they claim that two-tailed t-tests are "robust" even when variances and sample sizes are unequal. I, personally, do not like to call the tests robust when the two versions of the t-test, which are approximately equally robust, may have 90% different results when you compare which samples fall into the rejection interval (or region).
I find it easier to use the phrase, "There is a robust difference", which means that the same finding comes up no matter how you perform the test, what (justifiable) transformation you use, where you split the scores to test on dichotomies, etc., or what outside influences you hold constant as covariates.
Influence Function and Its Applications
The influence function of an estimate at the point x is essentially the change in the estimate when an infinitesimal observation is added at the point x, divided by the mass of the observation. The influence function gives the infinitesimal sensitivity of the solution to the addition of a new datum.It is main potential application of the influence function is in comparison of methods of estimation for ranking the robustness. A commonsense form of influence function is the robust procedures when the extreme values are dropped, i.e., data trimming.
There are a few fundamental statistical tests such as test for randomness, test for homogeneity of population, test for detecting outliner(s), and then test for normality. For all these necessary tests there are powerful procedures in statistical data analysis literatures. Moreover since the authors are limiting their presentation to the test of mean, they can invoke the CLT for, say any sample of size over 30.
The concept of influence is the study of the impact on the conclusions and inferences on various fields of studies including statistical data analysis. This is possible by a perturbation analysis. For example, the influence function of an estimate is the change in the estimate when an infinitesimal change in a single observation divided by the amount of the change. It acts as the sensitivity analysis of the estimate.
The influence function has been extended to the "what-if" analysis, robustness, and scenarios analysis, such as adding or deleting an observation, outliners(s) impact, and so on. For example, for a given distribution both normal or otherwise, for which population parameters have been estimated from samples, the confidence interval for estimates of the median or mean is smaller than for those values that tend towards the extremities such as the 90% or 10% data. While in estimating the mean on can invoke the central limit theorem for any sample of size over, say 30. However, we cannot be sure that the calculated variance is the true variance of the population and therefore greater uncertainty creeps in and one need to sue the influence function as a measuring tool an decision procedure.
Further Readings:
Melnikov Y., Influence Functions and Matrices, Dekker, 1999.
What is Imprecise Probability?
Imprecise probability is a generic term for the many mathematical models that measure chance or uncertainty without sharp numerical probabilities. These models include belief functions, capacities' theory, comparative probability orderings, convex sets of probability measures, fuzzy measures, interval-valued probabilities, possibility measures, plausibility measures, and upper and lower expectations or previsions. Such models are needed in inference problems where the relevant information is scarce, vague or conflicting, and in decision problems where preferences may also be incomplete.What is a Meta-Analysis?
A Meta-analysis deals with a set of RESULTs to give an overall RESULT that is comprehensive and valid.a) Especially when Effect-sizes are rather small, the hope is that one can gain good power by essentially pretending to have the larger N as a valid, combined sample.
b) When effect sizes are rather large, then the extra POWER is not needed for main effects of design: Instead, it theoretically could be possible to look at contrasts between the slight variations in the studies themselves.
For example, to compare two effect sizes (r) obtained by two separate studies, you may use:
Z = (z1 - z2)/[(1/n1-3) + (1/n2-3)]1/2
where z1 and z2 are Fisher transformations of r, and the two ni's in the denominator represent the sample size for each study.
If you really trust that "all things being equal" will hold up. The typical "meta" study does not do the tests for homogeneity that should be required
In other words:
1. there is a body of research/data literature that you would like to summarize
2. one gathers together all the admissible examples of this literature (note: some might be discarded for various reasons)
3. certain details of each investigation are deciphered ... most important would be the effect that has or has not been found, i.e., how much larger in sd units is the treatment group's performance compared to one or more controls.
4. call the values in each of the investigations in #3 .. mini effect sizes.
5. across all admissible data sets, you attempt to summarize the overall effect size by forming a set of individual effects ... and using an overall sd as the divisor .. thus yielding essentially an average effect size.
6. in the meta analysis literature ... sometimes these effect sizes are further labeled as small, medium, or large ....
You can look at effect sizes in many different ways .. across different factors and variables. but, in a nutshell, this is what is done.
I recall a case in physics, in which, after a phenomenon had been observed in air, emulsion data were examined. The theory would have about a 9% effect in emulsion, and behold, the published data gave 15%. As it happens, there was no significant difference (practical, not statistical) in the theory, and also no error in the data. It was just that the results of experiments in which nothing statistically significant was found were not reported.
This non-reporting of such experiments, and often of the specific results which were not statistically significant, which introduces major biases. This is also combined with the totally erroneous attitude of researchers that statistically significant results are the important ones, and than if there is no significance, the effect was not important. We really need to differentiate between the term "statistically significant", and the usual word significant.
Meta-analysis is a controversial type of literature review in which the results of individual randomized controlled studies are pooled together to try to get an estimate of the effect of the intervention being studied. It increases statistical power and is used to resolve the problem of reports which disagree with each other. It's not easy to do well and there are many inherent problems.
Further Readings:
Lipsey M., and D. Wilson, Practical Meta-Analysis, Sage Publications, 2000.
What Is the Effect Size
Effect size (ES) is a ratio of a mean difference to a standard deviation, i.e. it is a form of z-score. Suppose an experimental treatment group has a mean score of Xe and a control group has a mean score of Xc and a standard deviation of Sc, then the effect size is equal to (Xe - Xc)/ScEffect size permits the comparative effect of different treatments to be compared, even when based on different samples and different measuring instruments.
Therefore, the ES is the mean difference between the control group and the treatment group. Howevere, by Glass's method, ES is (mean1 - mean2)/SD of control group while by Hunter-Schmit's method, ES is (mean1 - mean2)/pooled SD and then adjusted by instrument reliability coefficient. ES is commonly used in meta-analysis and power analysis.
Further Readings:
Cooper H., and L. Hedges, The Handbook of Research Synthesis, NY, Russell Sage, 1994.
Lipsey M., and D. Wilson, Practical Meta-Analysis, Sage Publications, 2000.
What is the Benford's Law? What About the Zipf's Law?
What is the Benford's Law: Benford's Law states that if we randomly select a number from a table of physical constants or statistical data, the probability that the first digit will be a "1" is about 0.301, rather than 0.1 as we might expect if all digits were equally likely. In general, the "law" says that the probability of the first digit being a "d" is:
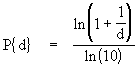
This implies that a number in a table of physical constants is more likely to begin with a smaller digit than a larger digit. This can be observed, for instance, by examining tables of Logarithms and noting that the first pages are much more worn and smudged than later pages.
Bias Reduction Techniques
The most effective tools for bias reduction is non-biased estimators are the Bootstrap and the Jackknifing.According to legend, Baron Munchausen saved himself from drowning in quicksand by pulling himself up using only his bootstraps. The statistical bootstrap, which uses resampling from a given set of data to mimic the variability that produced the data in the first place, has a rather more dependable theoretical basis and can be a highly effective procedure for estimation of error quantities in statistical problems.
Bootstrap is to create a virtual population by duplicating the same sample over and over, and then re-samples from the virtual population to form a reference set. Then you compare your original sample with the reference set to get the exact p-value. Very often, a certain structure is "assumed" so that a residual is computed for each case. What is then re-sampled is from the set of residuals, which are then added to those assumed structures, before some statistic is evaluated. The purpose is often to estimate a P-level.
Jackknife is to re-compute the data by leaving on observation out each time. Leave-one-out replication gives you the same Case-estimates, I think, as the proper jack-knife estimation. Jackknifing does a bit of logical folding (whence, 'jackknife' -- look it up) to provide estimators of coefficients and error that (you hope) will have reduced bias.
Bias reduction techniques have wide applications in anthropology, chemistry, climatology, clinical trials, cybernetics, and ecology.
Further Readings:
Efron B., The Jackknife, The Bootstrap and Other Resampling Plans, SIAM, Philadelphia, 1982.
Efron B., and R. Tibshirani, An Introduction to the Bootstrap, Chapman & Hall (now the CRC Press), 1994.
Shao J., and D. Tu, The Jackknife and Bootstrap, Springer Verlag, 1995.
Area Under Standard Normal Curve
Approximate area under standard normal curve from 0 to Z isZ(4.4-Z)/10 for 0 £ Z £ 2.2 0.49 for 2.2 < Z < 2.6 0.50 for Z £ 2.6 The maximum absolute error for the above approximation is roughly half a percent ( to be exact, 0.0052).
Number of Class Interval in Histogram
Before we can construct our frequency distribution we must determine how many classes we should use. This is purely arbitrary, but too few classes or too many classes will not provide as clear a picture as can be obtained with some more nearly optimum number. An empirical relationship (known as Sturges' rule) which seems to hold and which may be used as a guide to the number of classes (k) is given byk = the smallest integer greater than or equal to 1 + Log(n) / Log (2) = 1 + 3.332Log(n)
To have an 'optimum' you need some measure of quality - presumably in this case, the 'best' way to display whatever information is available in the data. The sample size contributes to this, so the usual guidelines are to use between 5 and 15 classes, one need more classes if you one has a very large sample. You take into account a preference for tidy class widths, preferably a multiple of 5 or 10, because this makes it easier to appreciate the scale.
Beyond this it becomes a matter of judgement - try out a range of class widths and choose the one that works best. (This assumes you have a computer and can generate alternative histograms fairly readily).
There are often management issues that come into it as well. For example, if your data is to be compared to similar data - such as prior studies, or from other countries - you are restricted to the intervals used therein.
If the histogram is very skewed, then unequal classes should be considered. Use narrow classes where the class frequencies are high, wide classes where they are low.
The following approaches are common:
Let n be the sample size, then number of class interval could be
MIN {n½, 10Log(n) }.
Thus for 200 observations you would use 14 intervals but for 2000 you would use 33.
Alternatively,
1. Find the range (highest value - lowest value).
2. Divide the range by a reasonable interval size: 2, 3, 5, 10 or a = multiple of 10.
3. Aim for no fewer than 5 intervals and no more than 15.
Structural Equation Modeling
The structural equation modeling techniques are used to study relations among variables. The relations are typically assumed to be linear. In social and behavioral research most phenomena are influenced by a large number of determinants which typically have a complex pattern of interrelationships. To understand the relative importance of these determinants their relations must be adequately represented in a model, which may be done with structural equation modeling.A structural equation model may apply to one group of cases or to multiple groups of cases. When multiple groups are analyzed parameters may be constrained to be equal across two or more groups. When two or more groups are analyzed, means on observed and latent variables may also be included in the model.
As an application, how do you test the equality of regression slopes coming from the same sample using 3 different measuring methods? You could use a structural modeling approach.
1 - Standardize all three data sets prior to the analysis because b weights are also a function of the variance of the predictor variable and with standardization, you remove this source.
2 - Model the dependent variable as the effect from all three measures and obtain the path coefficient (b weight) for each one.
3 - Then fit a model in which the three path coefficients are constrained to be equal. If a significant decrement in fit occurs, the paths are not equal.
Further Readings:
Schumacker R., and R. Lomax, A Beginner's Guide to Structural Equation Modeling, Lawrence Erlbaum, New Jersey, 1996.
Econometrics and Time Series Models
Econometrics models are sets of simultaneous regression models with applications to areas such as Industrial Economics, Agricultural Economics, and Corporate Strategy and Regulation. Time Series Models require large number of observations (say over 50). Both models are used successfully for business applications ranging from micro to macro studies, including finance and endogenous growth. Other modeling approaches include structural and classical modeling such as Harvey, and Box-Jenkins approaches, co-integration analysis and general micro econometrics in probabilistic models, e.g., Logit, Probit and Tobit, panel data and cross sections. Econometrics is mostly studying the issue of causality, i.e. the issue of identifying a causal relation between an outcome and a set of factors that may have determined this outcome. In particular, ti make this concept operational in time series, and exogeneity modeling.
Further Readings:
Ericsson N., and J. Irons, Testing Exogeneity, Oxford University Press, 1994.
Granger C., and P. Newbold, Forecasting in Business and Economics, Academic Press, 1989.
Hamouda O., and J. Rowley, (Eds.), Time Series Models, Causality and Exogeneity, Edward Elgar Pub., 1999.
Tri-linear Coordinates Triangle
A "ternary diagram" is usually used to show the change of opinion (FOR - AGAINST - UNDECIDED). The triangular diagram used first by the chemist Willard Gibbs in his studies on phase transitions. It is based on the proposition from geometry that in an equilateral triangle, the sum of the distances from any point to the three sides is constant. This implies that the percent composition of a mixture of three substances can be represented as a point in such a diagram, since the sum of the percentages is constant (100). The three vertices are the points of the pure substances.The same holds for the "composition" of the opinions in a population. When percents for, against and undecided sum to 100, the same technique for presentation can be used. See the diagram below, which should be viewed with a non-proportional letter. True equilateral may not be preserved in transmission. E.g. let the initial composition of opinions be given by 1. That is, few undecided, roughly equally as much for as against. Let another composition be given by point 2. This point represents a higher percentage undecided and, among the decided, a majority of "for".
Internal and Inter-rater Reliability
"Internal reliability" of a scale is often measured by Cronbach's coefficient a. It is relevant when you will compute a total score and you want to know its reliability, based on no other rating. The "reliability" is *estimated* from the average correlation, and from the number of items, since a longer scale will (presumably) be more reliable. Whether the items have the same means is not usually important.Tau-equivalent: The true scores on items are assumed to differ from each other by no more than a constant. For a to equal the reliability of measure, the items comprising it have to be at a least tau-equivalent, if this assumption is not met, a is lower bound estimate of reliability.
Congeneric measures: This least restrictive model within the framework of classical test theory requires only that true scores on measures said to be measuring the same phenomenon be perfectly correlated. Consequently, on congeneric measures, error variances, true-score means, and true-score variances may be unequal
For "inter-rater" reliability, one distinction is that the importance lies with the reliability of the single rating. Suppose we have the following data
Participants Time Q1 Q2 Q3 to Q17 001 1 4 5 4 4 002 1 3 4 3 3 001 2 4 4 5 3 etc.By examining the data, I think one cannot do better than looking at the paired t-test and Pearson correlations between each pair of raters - the t-test tells you whether the means are different, while the correlation tells you whether the judgments are otherwise consistent.
Unlike the Pearson, the "intra-class" correlation assumes that the raters do have the same mean. It is not bad as an overall summary, and it is precisely what some editors do want to see presented for reliability across raters. It is both a plus and a minus, that there are a few different formulas for intra-class correlation, depending on whose reliability is being estimated.
For purposes such as planning the Power for a proposed study, it does matter whether the raters to be used will be exactly the same individuals. A good methodology to apply in such cases, is the Bland & Altman analysis.
SPSS Commands:
Reliability (Alpha, KR-20) RELIABILITYSAS Commands:
Reliability (Alpha, KR-20) CORR ALPHA
When to Use Nonparametric Technique?
Parametric techniques are more useful the more you know about your subject matter, since knowledge of your subject matter can be built into parametric models. Nonparametric methods, including both senses of the term, distribution free tests and flexible functional forms, are more useful the less you know about your subject matter. One must use statistical technique called nonparametric if it satisfies at least on of the following five types of criteria:1. The data entering the analysis are enumerative - that is, count data representing the number of observations in each category or cross-category.
2. The data are measured and /or analyzed using a nominal scale of measurement.
3. The data are measured and /or analyzed using an ordinal scale of measurement.
4. The inference does not concern a parameter in the population distribution - as, for example, the hypothesis that a time-ordered set of observations exhibits a random pattern.
5. The probability distribution of the statistic upon which the the analysis is based is not dependent upon specific information or assumptions about the population(s) which the sample(s) are drawn, but only on general assumptions, such as a continuous and/or symmetric population distribution.
By this definition, the distinction of nonparametric is accorded either because of the level of measurement used or required for the analysis, as in types 1 through 3; the type of inference, as in type 4 or the generality of the assumptions made about the population distribution, as in type 5.
For example one may use the Mann-Whitney Rank Test as a nonparametric alternative to Students T-test when one does not have normally distributed data.
Mann-Whitney: To be used with two independent groups (analogous to the independent groups t-test)
Wilcoxon: To be used with two related (i.e., matched or repeated) groups (analogous to the related samples t-test)
Kruskall-Wallis: To be used with two or more independent groups (analogous to the single-factor between-subjects ANOVA)
Friedman: To be used with two or more related groups (analogous to the single-factor within-subjects ANOVA)
Analysis of Incomplete Data
Methods dealing with analysis of data with missing values can be classified into:
- Analysis of complete cases, including weighting adjustments,
- Imputation methods, and extensions to multiple imputation, and
- Methods that analyze the incomplete data directly without requiring a rectangular data set, such as maximum likelihood and
Bayesian methods.
Multiple imputation (MI) is a general paradigm for the analysis of incomplete data. Each missing datum is replaced by m> 1 simulated values, producing m simulated versions of the complete data. Each version is analyzed by standard complete-data methods, and the results are combined using simple rules to produce inferential statements that incorporate missing data uncertainty. The focus is on the practice of MI for real statistical problems in modern computing environments.
Further Readings:
Rubin D., Multiple Imputation for Nonresponse in Surveys, New York, Wiley, 1987.
Schafer J., Analysis of Incomplete Multivariate Data, London, Chapman and Hall, 1997.
Little R., and D. Rubin, Statistical Analysis with Missing Data, New York, Wiley, 1987.
Interactions in ANOVA and Regression Analysis
Interactions are ignored only if you permit it. For historical reasons, ANOVA programs generally produce all possible interactions, while (multiple) regression programs generally do not produce any interactions - at least, not so routinely. So it's up to the user to construct interaction terms when using regression to analyze a problem where interactions are, or may be, of interest. (By "interaction terms" I mean variables that carry the interaction information, included as predictors in the regression model.)Regression is the estimation of the conditional expectation of a random variable given another (possibly vector-valued) random variable.
The easiest construction is to multiply together the predictors whose interaction is to be included. When there are more than about three predictors, and especially if the raw variables take values that are distant from zero (like number of items right), the various products (for the numerous interactions that can be generated) tend to be highly correlated with each other, and with the original predictors. This is sometimes called "the problem of multicollinearity", although it would more accurately be described as spurious multicollinearity. It is possible, and often to be recommended, to adjust the raw products so as to make them orthogonal to the original variables (and to lower-order interaction terms as well).
What does it mean if the standard error term is high? Multicolinearity is not the only factor that can cause large SE's for estimators of "slope" coefficients any regression models. SE's are inversely proportional to the range of variability in the predictor variable. For example, if you were estimating the linear association between weight (x) and some dichotomous outcome and x=(50,50,50,50,51,51,53,55,60,62) the SE would be much larger than if x=(10,20,30,40,50,60,70,80,90,100) all else being equal. There is a lesson here for the planning of experiments. To increase the precision of estimators, increase the range of the input. Another cause of large SE's is a small number of "event" observations or a small number of "non-event" observations (analogous to small variance in the outcome variable). This is not strictly controllable but will increase all estimator SE's (not just an individual SE). There is also another cause of high standard errors, it's called serial correlation. This problem is frequent, if not typical, when using time-series, since in that case the stochastic disturbance term will often reflect variables, not included explicitly in the model, that may change slowly as time passes by.
In a linear model representing the variation in a dependent variable Y as a linear function of several explanatory variables, interaction between two explanatory variables X and W can be represented by their product: that is, by the variable created by multiplying them together. Algebraically such a model is represented by:
Y = a +b1X + b2 W + b3 XW + e .
When X and W are category systems. This equation describes a two-way analysis of variance (ANOV) model; when X and W are (quasi-)continuous variables, this equation describes a multiple linear regression (MLR) model.
In ANOV contexts, the existence of an interaction can be described as a difference between differences: the difference in means between two levels of X at one value of W is not the same as the difference in the corresponding means at another value of W, and this not-the-same-ness constitutes the interaction between X and W; it is quantified by the value of b3.
In MLR contexts, an interaction implies a change in the slope (of the regression of Y on X) from one value of W to another value of W (or, equivalently, a change in the slope of the regression of Y on W for different values of X): in a two-predictor regression with interaction, the response surface is not a plane but a twisted surface (like "a bent cookie tin", in Darlington's (1990) phrase). The change of slope is quantified by the value of b3. To resolve the problem of multi-collinearity.
Variance of Nonlinear Random Functions
The variation in nonlinear function of several random variables can be approximated by the "delta method". An approximate variance for a smooth function f(X, Y) of two random variables (X, Y) is obtained by a approximating f(X, Y) by the linear terms of its Taylor expansion in the neighborhood of about the sample means of X and Y.For example, the variance of XY and X/Y based on a large sample size are approximated by:
and
Visualization of Statistics: Analytic-Geometry & Statistics
Introduction to Visualization of Statistics
Most of statistical data processing involves algebraic operations on the dataset. However, if the dataset contains more than 3 numbers, it is not possible to visualize it by geometric representation, mainly due to human sensory limitation. Geometry has a much longer history than algebra. Ancient Greeks applied geometry to measure land, and developed the geo-metric models. The analytic-geometry is to find equivalency between algebra and geometry. The aim is a better understanding by visualization in 2-or-3 dimensional space, and to generalize the ideas for higher dimensions by analytic thinking.Without the loss of generality, and conserving space, the following presentation is in the context of small sample size, allowing us to see statistics in 1, or 2-dimensional space.
The Mean and The Median
Suppose that four people want to get together to play poker. They live on 1st Street, 3rd Street, 7th Street, and 15th Street. They want to select a house that involves the minimum amount of driving for all parties concerned.Let's suppose that they decide to minimize the absolute amount of driving. If they met at 1st Street, the amount of driving would be 0 + 2 + 6 + 14 = 22 blocks. If they met at 3rd Street, the amount of driving would be 2 + 0+ 4 + 12 = 18 blocks. If they met at 7th Street, 6 + 4 + 0 + 8 = 18 blocks. Finally, at 15th Street, 14 + 12 + 8 + 0 = 34 blocks.
So the two houses that would minimize the amount of driving would be 3rd or 7th Street. Actually, if they wanted a neutral site, any place on 4th, 5th, or 6th Street would also work.
Note that any value between 3 and 7 could be defined as the median of 1, 3, 7, and 15. So the median is the value that minimizes the absolute distance to the data points.
Now, the person at 15th is upset at always having to do more driving. So the group agrees to consider a different rule. In deciding to minimize the square of the distance driving, we are using the least square principle. By squaring, we give more weight to a single very long commute than to a bunch of shorter commutes. With this rule, the 7th Street house (36 + 16 + 0 + 64 = 116 square blocks) is preferred to the 3rd Street house (4 + 0 + 16 + 144 = 164 square blocks). If you consider any location, and not just the houses themselves, then 9th Street is the location that minimizes the square of the distances driven.
Find the value of x that minimizes:
The value that minimizes the sum of squared values is 6.5, which is also equal to the arithmetic mean of 1, 3, 7, and 15. With calculus, it's easy to show that this holds in general.
Consider a small sample of scores with an even number of cases; for example, 1, 2, 4, 7, 10, and 12. The median is 5.5, the midpoint of the interval between the scores of 4 and 7.
As we discussed above, it is true that the median is a point around which the sum of absolute deviations is minimized. In this example the sum of absolute deviations is 22. However, it is not a unique point. Any point in the 4 to 7 region will have the same value of 22 for the sum of the absolute deviations.
Indeed, medians are tricky. The 50% above -- 50% below is not quite correct. For example, 1, 1, 1, 1, 1, 1, 8 has no median. The convention says that, the median is 1; however, about 14% of the data lie strictly above it; 100% of the data are greater than or equal to the median.
We will make use of this idea in regression analysis. In an analogous argument, the regression line is a unique line, which minimizes the sum of the squared deviations from it. There is no unique line that minimizes the sum of the absolute deviations from it.
Arithmetic and Geometric Means
Arithmetic Mean: Suppose you have two data points x and y, on real number- line axis:

The arithmetic mean (a) is a point such that the following vectorial relation holds: ox - oa = oa - oy.
Geometric Mean: Suppose you have two positive data points x and y, on the above real number- line axis, then the Geometric Mean (g) of these numbers is a point g such that |ox| / |og| = |og| / |oy|, where |ox| means the length of line segment ox, for example.
Variance, Covariance, and Correlation Coefficient
Consider a data set containing n = 2 observations (5, 1). Upon centralizing the data, one obtains the vector V1 = (5-3 = 2, 1-3 = -2), as shown in the following n = 2 dimensional coordinate system:
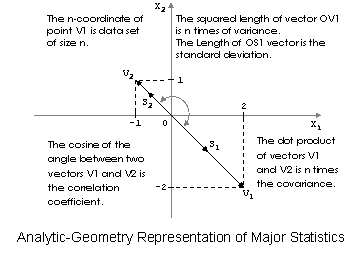
Notice that the vector V1 length is:
The covariance is,
Therefore:
Notice that the dot-product is multiplication of the two lengths times the cosine of the angle between the two vectors. Therefore,
The correlation coefficient is therefore:
This is possibly the simplest proof that the correlation coefficient is always bounded by the interval [-1, 1]. The correlation coefficient for our numerical example is Cos (V1, V2) = Cos(180°) = -1, as expected from the above figure.
The distance between the two-point data sets V1, and V2 is also a dot-product:
= n[Var(V1) + VarV2 - 2Cov(V1, V2)]
Now, construct a matrix whose columns are the coordinates of the two vectors V1 and V2, respectively. Multiplying the transpose of this matrix by itself provides a new symmetric matrix containing n times the variance of V1 and variance of V2 as its main diagonal elements (i.e., 8, 2), and n times Cov (V1, V2) as its off diagonal element (i.e., -4).
You might like to use a graph paper, and a scientific calculator to check the results of these numerical examples and to perform some additional numerical experimentation for a deeper understanding of the concepts.
Further Reading:
Wickens T., The Geometry of Multivariate Statistics, Erlbaum Pub., 1995.
What Is a Geometric Mean
The geometric mean of n nonnegative numerical values is the nth root of the product of the n values. The denominator of the Pearson correlation coefficient is the geometric mean of the two variances. It is useful for averaging "product moment" values.Suppose you have two positive data points x and y, then the geometric mean of these numbers is a number (g) such that x/g = y/b, and the arithmetic mean (a) is a number such that x - a = a - y.
The geometric means are used extensively by the U.S. Bureau of Labor Statistics ["Geomeans" as they call them] in the computation of the U.S. Consumer Price Index. The geomeans are also used in price indexes. The statistical use of geometric mean is for index numbers such as the Fisher's ideal index.
If some values are very large in magnitude and others are small, then the geometric mean is a better average. In a Geometric series, the most meaningful average is the geometric mean. The arithmetic mean is very biased toward the larger numbers in the series.
As an example, suppose sales of a certain item increase to 110% in the first year and to 150% of that in the second year. For simplicity, assume you sold 100 items initially. Then the number sold in the first year is 110 and the number sold in the second is 150% x 110 = 165. The arithmetic average of 110% and 150% is 130% so that we would incorrectly estimate that the number sold in the first year is 130 and the number in the second year is 169. The geometric mean of 110% and 150% is r = (1.65)1/2 so that we would correctly estimate that we would sell 100 (r)2 = 165 items in the second year.
As another similar example, if a mutual fund goes up by 50% one year and down by 50% the next year, and you hold a unit throughout both years, you have lost money at the end. For every dollar you started with, you have now got 75c. Thus, the performance is different from gaining (50%-50%)/2 (= 0%). It is the same as changing by a multiplicative factor of (1.5 x 0.5)½ = 0.866 each year. In a multiplicative process, the one value that can be substituted for each of a set of values to give the same "overall effect" is the geometric mean, not the arithmetic mean. As money tends to multiplicatively ("it takes money to make money"), financial data are often better combined in this way.
As a survey analysis example, give a sample of people a list of, say 10, crimes ranging in seriousness:
Ask each respondent to give any numerical value they feel to any crime in the list (e.g. someone might decide to call arson 100). Then ask them to rate each crime in the list on a ratio scale. If a respondent thought rape was five times as bad as arson, then a value of 500 would be assigned, theft a quarter as bad, 25. Suppose we now wanted the "average" rating across respondents given to each crime. Since respondents are using their own base value, the arithmetic mean would be useless: people who used large numbers as their base value would "swamp" those who had chosen small numbers. However, the geometric mean -- the nth root of the product of ratings for each crime of the n respondents -- gives equal weighting to all responses. I've used this in a class exercise and it works nicely.
It is often good to log-transform such data before regression, ANOVA, etc. These statistical techniques give inferences about the arithmetic mean (which is intimately connected with the least-squares error measure); however, the arithmetic mean of log-transformed data is the log of the geometric mean of the data. So, for instance, a t test on log-transformed data is really a test for location of the geometric mean.
Further Reading:
Langley R., Practical Statistics Simply Explained, 1970, Dover Press.
What Is Central Limit Theorem?
For practical purposes, the main idea of the central limit theorem (CLT) is that the average of a sample of observations drawn from some population with any shape-distribution is approximately distributed as a normal distribution if certain conditions are met. In theoretical statistics there are several versions of the central limit theorem depending on how these conditions are specified. These are concerned with the types of assumptions made about the distribution of the parent population (population from which the sample is drawn) and the actual sampling procedure.One of the simplest versions of the theorem says that if is a random sample of size n (say, n> 30) from an infinite population finite standard deviation , then the standardized sample mean converges to a standard normal distribution or, equivalently, the sample mean approaches a normal distribution with mean equal to the population mean and standard deviation equal to standard deviation of the population divided by square root of sample size n. In applications of the central limit theorem to practical problems in statistical inference, however, statisticians are more interested in how closely the approximate distribution of the sample mean follows a normal distribution for finite sample sizes, than the limiting distribution itself. Sufficiently close agreement with a normal distribution allows statisticians to use normal theory for making inferences about population parameters (such as the mean ) using the sample mean, irrespective of the actual form of the parent population.
It is well known that whatever the parent population is, the standardized variable will have a distribution with a mean 0 and standard deviation 1 under random sampling. Moreover, if the parent population is normal, then is distributed exactly as a standard normal variable for any positive integer n. The central limit theorem states the remarkable result that, even when the parent population is non-normal, the standardized variable is approximately normal if the sample size is large enough (say, > 30). It is generally not possible to state conditions under which the approximation given by the central limit theorem works and what sample sizes are needed before the approximation becomes good enough. As a general guideline, statisticians have used the prescription that if the parent distribution is symmetric and relatively short-tailed, then the sample mean reaches approximate normality for smaller samples than if the parent population is skewed or long-tailed.
On e must study the behavior of the mean of samples of different sizes drawn from a variety of parent populations. Examining sampling distributions of sample means computed from samples of different sizes drawn from a variety of distributions, allow us to gain some insight into the behavior of the sample mean under those specific conditions as well as examine the validity of the guidelines mentioned above for using the central limit theorem in practice.
Under certain conditions, in large samples, the sampling distribution of the sample mean can be approximated by a normal distribution. The sample size needed for the approximation to be adequate depends strongly on the shape of the parent distribution. Symmetry (or lack thereof) is particularly important. For a symmetric parent distribution, even if very different from the shape of a normal distribution, an adequate approximation can be obtained with small samples (e.g., 10 or 12 for the uniform distribution). For symmetric short-tailed parent distributions, the sample mean reaches approximate normality for smaller samples than if the parent population is skewed and long-tailed. In some extreme cases (e.g. binomial with ) samples sizes far exceeding the typical guidelines (say, 30) are needed for an adequate approximation. For some distributions without first and second moments (e.g., Cauchy), the central limit theorem does not hold.
What is a Sampling Distribution?
The main idea of statistical inference is to take a random sample from a population and then to use the information from the sample to make inferences about particular population characteristics such as the mean (measure of central tendency), the standard deviation (measure of spread) or the proportion of units in the population that have a certain characteristic. Sampling saves money, time, and effort. Additionally, a sample can, in some cases, provide as much or more accuracy than a corresponding study that would attempt to investigate an entire population-careful collection of data from a sample will often provide better information than a less careful study that tries to look at everything.We will study the behavior of the mean of sample values from a different specified populations. Because a sample examines only part of a population, the sample mean will not exactly equal the corresponding mean of the population. Thus, an important consideration for those planning and interpreting sampling results, is the degree to which sample estimates, such as the sample mean, will agree with the corresponding population characteristic.
In practice, only one sample is usually taken (in some cases a small ``pilot sample'' is used to test the data-gathering mechanisms and to get preliminary information for planning the main sampling scheme). However, for purposes of understanding the degree to which sample means will agree with the corresponding population mean, it is useful to consider what would happen if 10, or 50, or 100 separate sampling studies, of the same type, were conducted. How consistent would the results be across these different studies? If we could see that the results from each of the samples would be nearly the same (and nearly correct!), then we would have confidence in the single sample that will actually be used. On the other hand, seeing that answers from the repeated samples were too variable for the needed accuracy would suggest that a different sampling plan (perhaps with a larger sample size) should be used.
A sampling distribution is used to describe the distribution of outcomes that one would observe from replication of a particular sampling plan.
Know that to estimate means to esteem (to give value to).
Know that estimates computed from one sample will be different from estimates that would be computed from another sample.
Understand that estimates are expected to differ from the population characteristics (parameters) that we are trying to estimate, but that the properties of sampling distributions allow us to quantify, probabilistically, how they will differ.
Understand that different statistics have different sampling distributions with distribution shape depending on (a) the specific statistic, (b) the sample size, and (c) the parent distribution.
Understand the relationship between sample size and the distribution of sample estimates.
Understand that the variability in a sampling distribution can be reduced by increasing the sample size.
Note that in large samples, many sampling distributions can be approximated with a normal distribution.
Outlier Removal
Outliers are a few observations that are not well fitted by the "best" available model. In practice any observation with standardized residual greater than 2.5 in absolute value is a candidate for being an outlier. In such case one must first investigate the source of data, if there is no doubt about the accuracy or veracity of the observation, then it should be removed and the model should be refitted.Robust statistical techniques are needed to cope with any undetected outliers; otherwise the result will be misleading. For example, the usual stepwise regression is often used for the selection of an appropriate subset of explanatory variables to use in model; however, it could be invalidated even by the presence of a few outliers.
Because of the potentially large variance, outliers could be the outcome of sampling. It's perfectly correct to have such an observation that legitimately belongs to the study group by definition. Lognormally distributed data (such as international exchange rate), for instance, will frequently exhibit such values.
Therefore, you must be very careful and cautious: before declaring an observation "an outlier," find out why and how such observation occurred. It could even be an error at the data entering stage.
First, construct the BoxPlot of your data. Form the Q1, Q2, and Q3 points which divide the samples into four equally sized groups. (Q2 = median) Let IQR = Q3 - Q1. Outliers are defined as those points outside the values Q3+k*IQR and Q1-k*IQR. For most case one sets k=1.5.
Another alternative is the following algorithm
a) Compute s of whole sample.
b) Define a set of limits off the mean: mean + ks, mean - ks sigma (Allow user to enter k. A typical value for k is 2.)
c) Remove all sample values outside the limits.
Now, iterate N times through the algorithm, each time replacing the sample set with the reduced samples after applying step (c).
Usually we need to iterate through this algorithm 4 times.
As mentioned earlier, a common "standard" is any observation falling beyond 1.5 (interquartile range) i.e., (1.5 IQRs) ranges above the third quartile or below the first quartile. The following SPSS program, helps you in determining the outliers.
$SPSS/OUTPUT=LIER.OUT
TITLE 'DETERMINING IF OUTLIERS EXIST'
DATA LIST FREE FILE='A' / X1
VAR LABLE
X1 'INPUT DATA'
LIST CASE CASE=10/VARIABLE=X1/
CONDESCRIPTIVE X1(ZX1)
LIST CASE CASE=10/VARIABLES=X1,ZX1/
SORT CASES BY ZX1(A)
LIST CASE CASE=10/VARIABLES=X1,ZX1/
FINISH
Outlier detection in the single population setting has been treated in detail in the literature. Quite often, however, one can argue that the detected outliers are not really outliers, but form a second population. If this is the case, a cluster approach needs to be taken. It will be active areas of research to study the problem of how outliers can arise and be identified, when a cluster approach must be taken.
Further Readings:
Hawkins D., Identification of Outliers, Chapman & Hall, 1980.
Rothamsted V., V. Barnett, and T. Lewis, Outliers in Statistical Data, Wiley, 1994.
Least Squares Models
Many problems in analyzing data involve describing how variables are related. The simplest of all models describing the relationship between two variables is a linear, or straight-line, model. The simplest method of fitting a linear model is to ``eye-ball'' a line through the data on a plot, but a more elegant, and conventional method is that of least squares, which finds the line minimizing the sum of distances between observed points and the fitted line.Realize that fitting the ``best'' line by eye is difficult, especially when there is a lot of residual variability in the data.
Know that there is a simple connection between the numerical coefficients in the regression equation and the slope and intercept of regression line.
Know that a single summary statistic like a correlation coefficient or does not tell the whole story. A scatter plot is an essential complement to examining the relationship between the two variables.
Know that the model checking is an essential part of the process of statistical modelling. After all, conclusions based on models that do not properly describe an observed set of data will be invalid.
Know the impact of violation of regression model assumptions (i.e., conditions) and possible solutions by analyzing the residuals.
Least Median of Squares Models
The standard least squares techniques for estimation in linear models are not robust in the sense that outliers or contaminated data can strongly influence estimates. A robust technique, which protects against contamination is least median of squares (LMS) estimation. An extension of LMS estimation to generalized linear models, giving rise to the least median of deviance (LMD) estimator.What Is Sufficiency?
A sufficient estimator based on a statistic contains all the information which is present in the raw data. For example, the sum of your data is sufficient to estimate the mean of the population. You do not have to know the data set itself. This saves a lot of money if the data has to be transmitted by telecommunication network. Simply, send out the total, and the sample size.A sufficient statistic t for a parameter q is a function of the sample data x1,...,xn, which contains all information in the sample about the parameter q . More formally, sufficiency is defined in terms of the likelihood function for q . For a sufficient statistic t, the Likelihood L(x1,...,xn| q ) can be written as
Since the second term does not depend on q , t is said to be a sufficient statistic for q .
Another way of stating this for the usual problems is that one could construct a random process starting from the sufficient statistic, which will have exactly the same distribution as the full sample for all states of nature.
To illustrate, let the observations be independent Bernoulli trials with the same probability of success. Suppose that there are n trials, and that person A observes which observations are successes, and person B only finds out the number of successes. Then if B places these successes at random points without replication, the probability that B will now get any given set of successes is exactly the same as the probability that A will see that set, no matter what the true probability of success happens to be.
You Must Look at Your Scattergrams!
Learn that given a set data the regression line is unique. However, the inverse of this statement is not true. The following interesting example is from, D. Moore (1997) book, page 349:
Data set A: x 10 8 13 9 11 14 y 8.04 6.95 7.58 8.81 8.33 9.96 x 6 4 12 7 5 y 7.24 4.26 10.84 4.82 5.68 Data set B: x 10 8 13 9 11 14 y 9.14 8.14 8.74 8.77 9.26 8.10 x 6 4 12 7 5 y 6.13 3.10 9.13 7.26 4.74 Data set C: x 8 8 8 8 8 8 y 6.58 5.76 7.71 8.84 8.47 7.04 x 8 8 8 8 19 y 5.25 5.56 7.91 6.89 12.50
All three sets have the same correlation and regression line. The important moral is look at your scattergrams.
How to produce a numerical example where the two scatterplots show clearly different relationships (strengths) but yield the same covariance? Perform the following steps:
1. Produce two sets of (X, Y) values that have different correlation's;
2. Calculate the two covariances, say C1 and C2;
3. Suppose you want to make C2 equal to C1. Then you want to multiply C2 by
(C1/C2);
4. Since C = r.Sx.Sy, you want two numbers (one of them might be 1), a and b such that
a.b = (C1/C2);
5. Multiply all values of X in set 2 by a, and all values of Y by b:
for the new variables,
C = r.a.b.Sx.Sy = C2.(C1/C2) = C1.
An interesting numerical example showing two identical scatterplots but with differing covariance is the following: Consider a data set of (X, Y) values, with covariance C1. Now let V = 2X, and W = 3Y. The covariance of V and W will be 2(3) = 6 times C1, but the correlation between V and W is the same as the correlation between X and Y.
Power of a Test
Significance tests are based on certain assumptions: The data have to be random samples out of a well defined basic population and one has to assume that some variables follow a certain distribution - in most cases the normal distribution is assumed.Power of a test is the probability of correctly rejecting a false null hypothesis. This probability is one minus the probability of making a Type II error (b). Recall also that we choose the probability of making a Type I error when we set a and that if we decrease the probability of making a Type I error we increase the probability of making a Type II error.
Power and Alpha:
Therefore, the probability of correctly retaining a true null has the same relationship to Type I errors as the probability of correctly rejecting an untrue null does to Type II error. Yet, as I mentioned if we decrease the odds of making one type of error we increase the odds of making the other type of error. What is the relationship between Type I and Type II errors?Power and the True Difference between Population Means: Anytime we test whether a sample differs from a population or whether two sample come from 2 separate populations, there is the assumption that each of the populations we are comparing has it's own mean and standard deviation (even if we do not know it). The distance between the two population means will affect the power of our test.
Power as a Function of Sample Size and Variance: You should notice that what really made the difference in the size of b is how much overlap there is in the two distributions. When the means are close together the two distributions overlap a great deal compared to when the means are farther apart. Thus, anything that effects the extent the two distributions share common values will increase b (the likelihood of making a Type II error).
Sample size has an indirect effect on power because it affects the measure of variance we use to calculate the t-test statistic. Since we are calculating the power of a test that involves the comparison of sample means, we will be more interested in the standard error (the average difference in sample values) than standard deviation or variance by itself. Thus, sample size is of interest because it modifies our estimate of the standard deviation. When n is large we will have a lower standard error than when n is small. In turn, when N is large well have a smaller b region than when n is small.
Pilot Studies: When the needed estimates for sample size calculation is not available from existing database, a pilot study is needed for adequate estimation with a given precision.
Further Readings:
Cohen J., Statistical Power Analysis for the Behavioral Sciences, L. Erlbaum Associates, 1988.
Kraemer H., and S. Thiemann, How Many Subjects? Provides basic sample size tables , explanations, and power analysis.
Murphy K., and B. Myors, Statistical Power Analysis, L. Erlbaum Associates, 1998. Provides a simple and general sample size determination for hypothesis tests.
ANOVA: Analysis of Variance
The tests we have learned up to this point allow us to test hypotheses that examine the difference between only two means. Analysis of Variance or ANOVA will allow us to test the difference between 2 or more means. ANOVA does this by examining the ratio of variability between two conditions and variability within each condition. For example, say we give a drug that we believe will improve memory to a group of people and give a placebo to another group of people. We might measure memory performance by the number of words recalled from a list we ask everyone to memorize. A t-test would compare the likelihood of observing the difference in the mean number of words recalled for each group. An ANOVA test, on the other hand, would compare the variability that we observe between the two conditions to the variability observed within each condition. Recall that we measure variability as the sum of the difference of each score from the mean. When we actually calculate an ANOVA we will use a short-cut formula.Thus, when the variability that we predict (between the two groups) is much greater than the variability we don't predict (within each group) then we will conclude that our treatments produce different results.
Levene's Test: Suppose that the sample data does not support the homogeneity of variance assumption, however, there is a good reason that the variations in the population are almost the same, then in such a situation you may like to use the Levene's modified test: In each group first compute the absolute deviation of the individual values from the median in that group. Apply the usual one way ANOVA on the set of deviation values and then interpret the results.
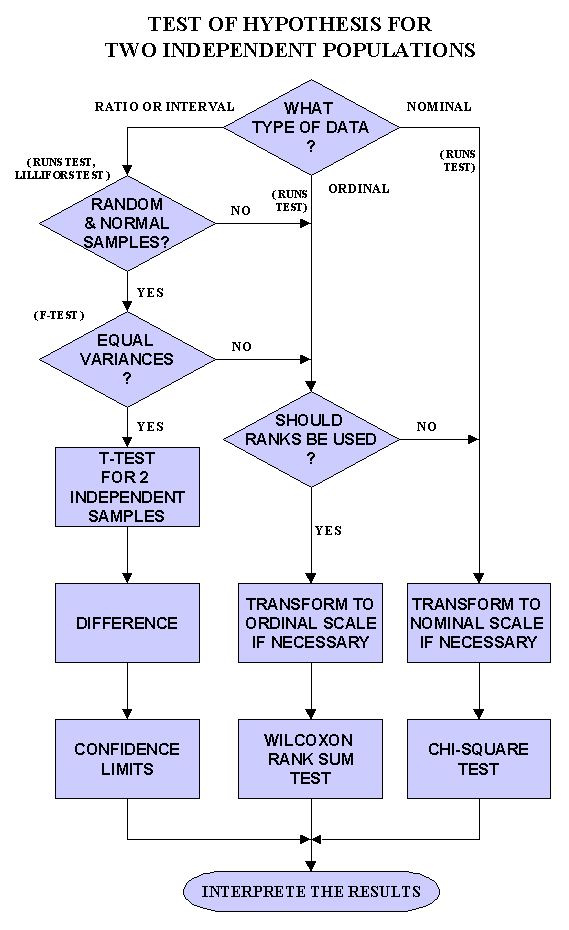
The Procedure for Two Populations Independent Means Test
Click on the image to enlarge it and THEN print it
You may use the following JavaScript to Test of Hypothesis for Two Populations
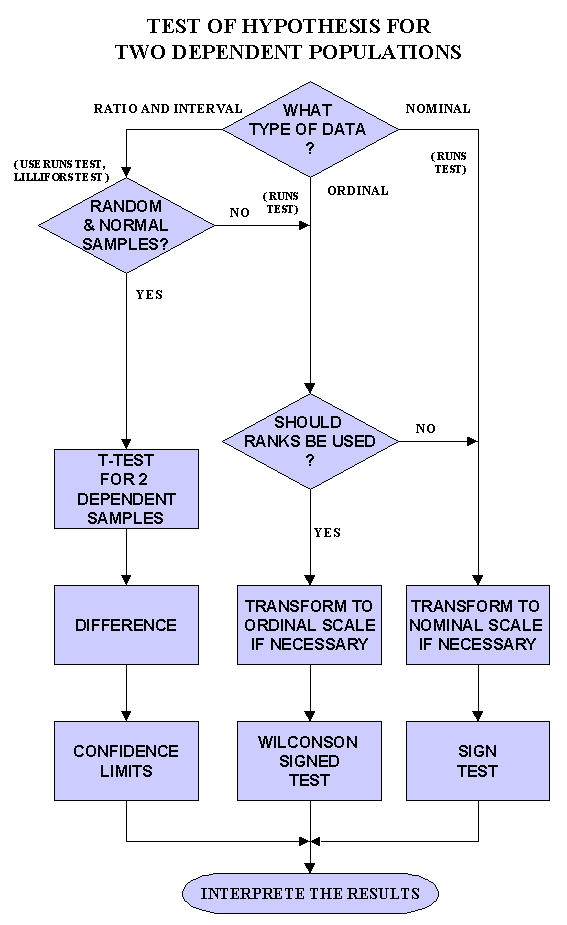
The Procedure for Two Dependent Means Test
Click on the image to enlarge it and THEN print it
You may use the following JavaScript to Two Dependent Populations Testing.

The Procedure for More Than Two Independent Means Test
Click on the image to enlarge it and THEN print it
You may use the following JavaScript to Three Means Comparison, Equality of Several Means' Test
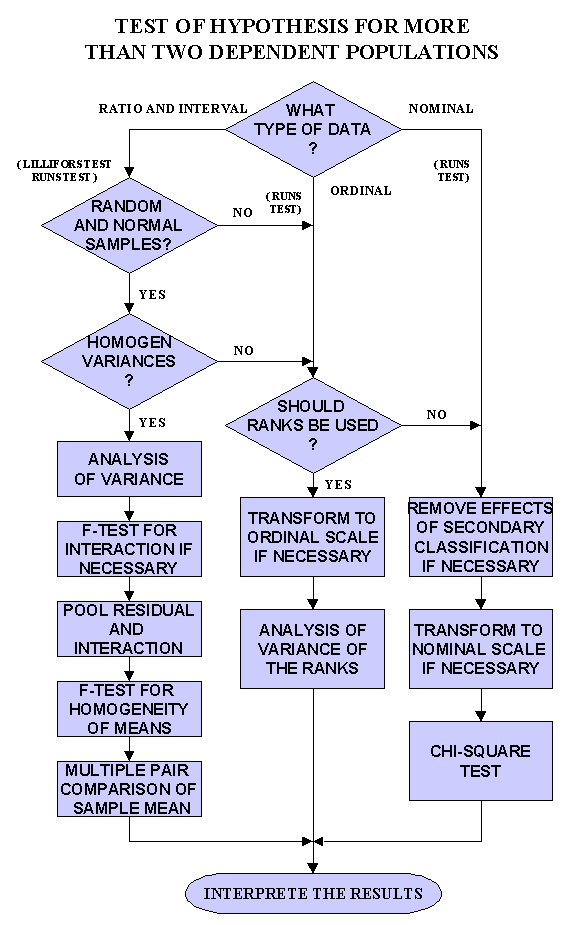
The Procedure for More Than Two Dependent Populations Test
Click on the image to enlarge it and THEN print it
You may use the following JavaScript to Three Dependent Means Comparison.
Orthogonal Contrasts of Means in ANOVA
In repeated measurement of the analysis of variance when the null hypothesis is rejected, we might be interested in multiple comparisons of means by the combinations of means, this is known as the orthogonal contrasting the means. A contrast of the means is said to be orthogonal if the weighting means sum to zero. For example, the contrast of(mean1+ mean2)/2 - mean3 is orthogonal. Therefore, to determine if two different contrasts of means from the same experiment are orthogonal, add the product of the weights to see if they sum to zero. If they do not sum to zero, then the two contrasts are not orthogonal and only one of them could be tested. The orthogonal contrasting allows us to compare each mean against all of the other means. There are several effective methods of orthogonal contrasting for applications in testing, constructing confidence intervals, and the partial F-test as the post-analysis statistical activities of the usual ANOVA.
Further Readings:
Kachigan S., Statistical Analysis: An Interdisciplinary Introduction to Univariate & Multivariate Methods, Radius Press, 1986.
Kachigan S., Multivariate Statistical Analysis: A Conceptual Introduction, Radius Press, 1991.
The Six-Sigma Quality
The total approach to quality is essential for competing in world markets. The ability of a firm to give customers what they want at the lowest total cost gives a company an advantage over its competitors.Sigma is a Greek symbol, which is used in statistics to represent standard deviation of a population. When a large enough random sample data are close to their mean (i.e., the average), then the population has a small deviation. If the data varies significantly from the mean, the data has a large deviation. In quality control measurement terms, you want to see that the sample is as close as possible to the mean and that the mean meets or exceed specifications. A large sigma means that there is a large amount of variation within the data. A lower sigma value corresponds to a small variation, and therefore a controlled process with a good quality.
The Six-Sigma means a measure of quality that strives for near perfection. Six-Sigma is a data-driven approach and methodology for eliminating defects to achieve six sigmas between lower and upper specification limits. Accordingly, to achieve Six-Sigma, e.g., in a manufacturing process it must not produce more than 3.4 defects per million opportunities. Therefore, a Six-Sigma defect is defined for not meeting the customer's specifications. A Six-Sigma opportunity is then the total quantity of chances for a defect.
Six-Sigma is a statistical measure expressing how close a product comes to its quality goal. One sigma means only 68% of products are acceptable; three sigma means 99.7% are acceptable. Six-Sigma is 99.9997% perfect or 3.4 defects per million parts or opportunities. The natural spread is 6 times the sample standard deviation. The natural spread is centered on the sample mean, and all weights in the sample fall within the natural spread, meaning the process will produce relatively few out-of-specification products. Six-Sigma does not necessarily imply 3 defective units per million made; it also signifies 3 defects per million opportunities when used to describe a process. Some products may have tens of thousands of opportunities for defects per finished item, so the proportion of defective opportunities may actually be quite large.
Six-Sigma Quality is a fundamental approach to delivering very high levels of customer satisfaction through disciplined use of data and statistical analysis for maximizing and sustaining business success. What that means is that all business decisions are made based on statistical analysis, not instinct or past history. Using the Six-Sigma approach will result in a significant, quantifiable improvement.
Is it truly necessary to go for zero defects? Why isn’t 99.9% (about 4.6 sigma) defect-free good enough? Here are some examples of what life would be like if 99.9% were good enough:
- 1 hour of unsafe drinking water every month
- 2 long or short landings at every American cities airport each day
- 400 letters per hour which never arrive at their destination
- 3,000 newborns accidentally falling from the hands of nurses or doctors each year
- 4,000 incorrect drug prescriptions per year
- 22,000 checks deducted from the wrong bank account each hour
Here are some examples of what life would be still like at Six-Sigma, 99.9997% defect-free:
- 13 wrong drug prescriptions per year
- 10 newborns accidentally falling from the hands of nurses or doctors each year
- 1 lost article of mail per hour
Now we see why the quest for Six-Sigma quality is necessary.
Six-Sigma is the application of statistical methods to business processes to improve operating efficiencies. It provides companies with a series of interventions and statistical tools that can lead to breakthrough profitability and quantum gains in quality. Six-Sigma allows us to take a real world problem with many potential answers, and translate it to a math problem, which will have only one answer. We then convert that one mathematical solution back to a real world solution.
Six-Sigma goes beyond defect reduction to emphasize business process improvement in general, which includes total cost reduction, cycle-time improvement, increased customer satisfaction, and any other metric important to the customer and the company. An objective of Six-Sigma is to eliminate any waste in the organization’s processes by creating a road map for changing data into knowledge, reducing the amount of stress companies experience when they are overwhelmed with day-to-day activities and proactively uncovering opportunities that impact the customer and the company itself.
The key to the Six-Sigma process is in eliminating defects. Organizations often waste time creating metrics that are not appropriate for the outputs being measured. Executives can get deceptive results if they force all projects to determine a one size fits all metric in order to compare the quality of products and services from various departments. From a managerial standpoint, having one universal tool seems beneficial; however, it is not always feasible. Below is an example of the deceptiveness of metrics.
In the airline industry, the US Air Traffic Control System Command Center measures companies on their rate of on time departure. This would obviously be a critical measurement to customers—the flying public. Whenever an airplane departs 15 minutes or more later than scheduled, that event is considered as a defect. Unfortunately, the government measures the airlines on whether the plane pulls away from the airport gate within 15 minutes of scheduled departure, not when it actually takes off. Airlines know this, so they pull away from the gate on time but let the plane sit on the runway as long as necessary before take off. The result to the customer is still a late departure. This defect metric is therefore not an accurate representation of the desires of the customers who are impacted by the process. If this were a good descriptive metric, airlines would be measured by the actual delay experienced by passengers.
This example shows the importance of having the right metrics for each process. The method above creates no incentive to reduce actual delays, so the customer (and ultimately the industry) still suffers. With a Six-Sigma business strategy, we want to see a picture that describes the true output of a process over time, along with additional metrics, to give an insight as to where the management has to focus its improvement efforts for the customer.
The Six Steps of Six-Sigma Loop Process: The process is identified by the following five major activities for each project:
- Identify the product or service you provide—What do you do?
- Identify your customer base, and determine what they care about—Who uses your products and services? What is really important to them?
- Identify your needs—What do you need to do your work?
- Define the process for doing your work—How do you do your work?
- Eliminate wasted efforts—How can you do your work better?
- Ensure continuous improvement by measuring, analyzing, and controlling the improved process—How perfectly are you doing your customer-focused work?
Often each step can create dozens of individual improvement projects and can last for several months. It is important to go back to each step from time to time in order to determine actual data maybe with improved measurement systems.
Once we know the answers to the above questions, we can begin to improve the process. The following case study will further explain the steps applied in Six-Sigma to Measure, Analyze, Improve, and Control a process to ensure customer satisfaction.
The Six Sigma General Process and Its Implementation: The Six-Sigma means a measure of quality that strives for near perfection. Six-Sigma is a data-driven approach and methodology for eliminating defects to achieve six-sigma’s between lower and upper specification limits. Accordingly, to achieve Six-Sigma, e.g., in a manufacturing process it must not produce more than 3.4 defects per million opportunities. Therefore, a Six-Sigma defect is defined for not meeting the customer's specifications. A Six-Sigma opportunity is then the total quantity of chances for a defect. The implementation of the Six Sigma system starts normally with a few days workshop of the top level management of the organization.
Only if the advantages of Six Sigma can be clearly stated and supported of the entire Management, then it makes sense to determine together the first project surrounding field and the pilot project team.
The pilot project team members participate is a few days Six Sigma workshop to learn the system principals, the process, the tools and the methodology.
The project team meets to compiles main decisions and identifying key stakeholders in the pilot surrounding field. Within the next days the requirements of the stakeholders are collected for the main decision processes by face-to-face interviews.
By now, the workshop of the top management must be ready for the next step. The next step for the project team is to decide which and how the achievements should be measured and then begin with the data collection and analysis. Whenever the results are understood well then suggestions for improvement will be collected, analyzed, and prioritized based on the urgency and inter-dependencies.
As the main outcome, the project team members will determine which improvements should be realized first. In this phase it is important that rapid successes are obtained, in order to even the soil for other Six Sigma projects in the organization.
The activities must be carried out in parallel whenever possible by a network activity chart. The activity chart will become more and more realistic by a loop-process while spread the improvement throughout the organization. More and more processes will be included and employees are trained including Black Belts who are the six sigma masters, and the dependency of external advisors will be reduced.
The main objective of the Six-Sigma approach is the implementation of a measurement-based strategy that focuses on process improvement. The aim is variation reduction, which can be accomplished by Six-Sigma methodology.
The Six-Sigma is a business strategy aimed at the near-elimination of defects from every manufacturing, service and transactional process. The concept of Six-Sigma was introduced and popularized for reducing defect rate of manufactured electronic boards. Although the original goal of Six-Sigma was to focus on manufacturing process, today the marketing, purchasing, customer order, financial and health care processing functions also embarked on Six Sigma programs.
Motorola Inc.Case: Motorola is a role model for modern manufacturers. The maker of wireless communications products, semiconductors, and electronic equipment enjoys a stellar reputation for high-tech, high-quality products. There is a reason for this reputation. A participative-management process emphasizing employee involvement is a key factor in Motorola’s quality push. In 1987, Motorola invested $44 million in employee training and education in a new quality program called Six-Sigma. Motorola measures its internal quality based on the number of defects in its products and processes. Motorola conceptualized Six-Sigma as a quality goal in the mid-1980. Their target was Six-Sigma quality, or 99.9997% defect free products—which is equivalent to 3.4 defects or less per 1 million parts. Quality is a competitive advantage because Motorola’s reputation opens markets. When Motorola Inc. won the Malcolm Baldridge National Quality Award in 1988; it was in the early stages of a plan that, by 1992, would achieve Six-Sigma Quality. It is estimated that of $9.2 billion in 1989 sales, $480 million was saved as a result of Motorola’s Six-Sigma program. Shortly thereafter, many US firms were following Motorola’s lead.
Control Charts, and the CUSUM
Control charts for variables are called X- and R-charts. The X-charts is used to monitor the average variability and the R-chart is used to monitor the range of the variation.Developing quality control charts for variables (X-Chart): The following steps are required for developing quality control charts for variables:
- Decide what should be measured.
- Determine the sample size.
- Collect random sample and record the measurements/counts.
- Calculate the average for each sample.
- Calculate the overall average. This is the average of all the sample averages (X-double bar).
- Determine the range for each sample.
- Calculate the average range (R-bar).
- Determine the upper control limit (UCL) and lower control limit (LCL) for the average and for the range.
- Plot the chart.
- Determine if the average and range values are in statistical control.
- Take necessary action based on your interpretation of the charts.
Developing control charts for attributes (P-Chart): Control charts for attributes are called P-charts. The following steps are required to set up P-charts:
- Determine what should be measured.
- Determine the required sample size.
- Collect sample data and record the data.
- Calculate the average percent defective for the process (p).
- Determine the control limits by determining the upper control limit (UCL) and the lower control limit (LCL) values for the chart.
- Plot the data.
- Determine if the percent defectives are within control.
Control charts are also used in industry to monitor processes that are far from Zero-Defect. However, among the powerful techniques is the counting of the cumulative conforming items between two nonconforming and its combined techniques based on cumulative sum and exponentially weighted moving average smoothing methods.
The general CUSUM is a statistical process control when measurements are multivariate. It is an effective tool in detecting a shift in the mean vector of the measurements, which is based on the cross-sectional antiranks of the measurements: At each time point, the measurements, after being appropriately transformed, are ordered and their antiranks are recorded. When the process is in-control under some mild regularity conditions the antirank vector at each time point has a given distribution, which changes to some other distribution when the process is out-of-control and the components of the mean vector of the process are not all the same. Therefore it detects shifts in all directions except the one that the components of the mean vector are all the same but not zero. This latter shift, however, can be easily detected by a univariate CUSUM.
Further Readings:
Breyfogle F., Implementing Six Sigma: Smarter Solutions Using Statistical Methods, Wiley, 1999.
del Castillo E., Statistical Process and Adjustment Methods for Quality Control, Wiley, 2002.
Juran J, and A. Godfreym, Juran's Quality Handbook, McGraw-Hill, 1999.
Xie M., T. Goh , and V. Kuralmani, Statistical Models and Control Charts for High Quality Processes, Kluwer, 2002.
Repeatability and Reproducibility
The term Repeatability refers to the equipment or instrument while Reproducibility refers to the equipment operator. Both Repeatability and Reproducibility involve statistical studies such as evaluation of statistical summaries, and comparison of the variances in repeat measurements, mostly for the industrial decision making problems. In these applications, for example the values indicated by the measuring devices vary from measurement to measurement. The main question is how much that built-in variation affects others activities, such as in-process measurements, quality checks, process improvement projects, etc.
Further Readings:
Barrentine L., Concepts for R&R Studies, ASQ Quality Press, 1991.
Wheeler D., and R. Lyday, Evaluating the Measurement Process, Statistical Process Control Press, 1990.
Statistical Instrument, Grab Sampling, and Passive Sampling Techniques
What is a statistical instrument? A statistical instrument is any process that aim at describing a phenomena by using any instrument or device, however the results may be used as a control tool. Examples of statistical instruments are questionnaire and surveys sampling.
What is grab sampling technique? The grab sampling technique is to take a relatively small sample over a very short period of time, the result obtained are usually instantaneous. However, the Passive Sampling is a technique where a sampling device is used for an extended time under similar conditions. Depending on the desirable statistical investigation, the Passive Sampling may be a useful alternative or even more appropriate than grab sampling. However, a passive sampling technique needs to be developed and tested in the field.
Distance Sampling
The term 'distance sampling' covers a range of methods for assessing wildlife abundance:line transect sampling, in which the distances sampled are distances of detected objects (usually animals) from the line along which the observer travels
point transect sampling, in which the distances sampled are distances of detected objects (usually birds) from the point at which the observer stands
cue counting, in which the distances sampled are distances from a moving observer to each detected cue given by the objects of interest (usually whales)
trapping webs, in which the distances sampled are from the web center to trapped objects (usually invertebrates or small terrestrial vertebrates)
migration counts, in which the 'distances' sampled are actually times of detection during the migration of objects (usually whales) past a watch point
Many mark-recapture models have been developed over the past 40 years. Monitoring of biological populations is receiving increasing emphasis in many countries. Data from marked populations can be used for the estimation of survival probabilities, how these vary by age, sex and time, and how they correlate with external variables. Estimation of immigration and emigration rates, population size and the proportion of age classes that enter the breeding population are often important and difficult to estimate with precision for free-ranging populations. Estimation of the finite rate of population change and fitness are still more difficult to address in a rigorous manner.
Further Readings:
Buckland S., D. Anderson, K. Burnham, and J. Laake, Distance Sampling: Estimating Abundance of Biological Populations, Chapman and Hall, London, 1993.
Buckland S., D. Anderson, K. Burnham, J. Laake, D. Borchers, and L. Thomas, Introduction to Distance Sampling, Oxford University Press, 2001.
Data Mining and Knowledge Discovery
How to discover value in mountain of data? Data mining uses sophisticated statistical analysis and modelling techniques to uncover patterns and relationships hidden in organizational databases. Data mining and knowledge discovery aim at tools and techniques to process structured information from databases to data warehouses to data mining, and to knowledge discovery. Data warehouse applications have become business-critical. Data mining can compress even more value out of these huge repositories of information.The continuing rapid growth of on-line data and the widespread use of databases necessitate the development of techniques for extracting useful knowledge and for facilitating database access. The challenge of extracting knowledge from data is of common interest to several fields, including statistics, databases, pattern recognition, machine learning, data visualization, optimization, and high-performance computing.
The data mining process involves identifying an appropriate data set to "mine" or sift through to discover data content relationships. Data mining tools include techniques like case-based reasoning, cluster analysis, data visualization, fuzzy query and analysis, and neural networks. Data mining sometimes resembles the traditional scientific method of identifying a hypothesis and then testing it using an appropriate data set. Sometimes however data mining is reminiscent of what happens when data has been collected and no significant results were found and hence an ad hoc, exploratory analysis is conducted to find a significant relationship.
Data mining is the process of extracting knowledge from data. The combination of fast computers, cheap storage, and better communication makes it easier by the day to tease useful information out of everything from supermarket buying patterns to credit histories. For clever marketers, that knowledge can be worth as much as the stuff real miners dig from the ground.
Data mining as an analytic process designed to explore large amounts of (typically business or market related) data in search for consistent patterns and/or systematic relationships between variables, and then to validate the findings by applying the detected patterns to new subsets of data. The process thus consists of three basic stages: exploration, model building or pattern definition, and validation/verification.
What distinguishes data mining from conventional statistical data analysis is that data mining is usually done for the purpose of "secondary analysis" aimed at finding unsuspected relationships unrelated to the purposes for which the data were originally collected.
Data warehousing as a process of organizing the storage of large, multivariate data sets in a way that facilitates the retrieval of information for analytic purposes.
Data mining is now a rather vague term, but the element that is common to most definitions is "predictive modeling with large data sets as used by big companies". Therefore, data mining is the extraction of hidden predictive information from large databases. It is a powerful new technology with great potential, for example, to help marketing managers "preemptively define the information market of tomorrow." Data mining tools predict future trends and behaviors, allowing businesses to make proactive, knowledge-driven decisions. The automated, prospective analyses offered by data mining move beyond the analyses of past events provided by retrospective tools. Data mining answers business questions that traditionally were too time-consuming to resolve. Data mining tools scour databases for hidden patterns, finding predictive information that experts may miss because it lies outside their expectations.
Data mining techniques can be implemented rapidly on existing software and hardware platforms across the large companies to enhance the value of existing resources, and can be integrated with new products and systems as they are brought on-line. When implemented on high performance client-server or parallel processing computers, data mining tools can analyze massive databases while a customer or analyst takes a coffee break, then deliver answers to questions such as, "Which clients are most likely to respond to my next promotional mailing, and why?"
Knowledge discovery in databases aims at tearing down the last barrier in enterprises' information flow, the data analysis step. It is a label for an activity performed in a wide variety of application domains within the science and business communities, as well as for pleasure. The activity uses a large and heterogeneous data-set as a basis for synthesizing new and relevant knowledge. The knowledge is new because hidden relationships within the data are explicated, and/or data is combined with prior knowledge to elucidate a given problem. The term relevant is used to emphasize that knowledge discovery is a goal-driven process in which knowledge is constructed to facilitate the solution to a problem.
Knowledge discovery maybe viewed as a process containing many tasks. Some of these tasks are well understood, while others depend on human judgment in an implicit matter. Further, the process is characterized by heavy iterations between the tasks. This is very similar to many creative engineering process, e.g., the development of dynamic models. In this reference mechanistic, or first principles based, models are emphasized, and the tasks involved in model development are defined by:
- Initialize data collection and problem formulation. The initial data are collected, and some more or less precise formulation of the modeling problem is developed.
- Tools selection. The software tools to support modeling and allow simulation are selected.
- Conceptual modeling. The system to be modeled, e.g., a chemical reactor, a power generator, or a marine vessel, is abstracted at first. The essential compartments and the dominant phenomena occurring are identified and documented for later reuse.
- Model representation. A representation of the system model is generated. Often, equations are used; however, a graphical block diagram (or any other formalism) may alternatively be used, depending on the modeling tools selected above.
- Computer implementation. The model representation is implemented using the means provided by the modeling system of the software employed. These may range from general programming languages to equation-based modeling languages or graphical block-oriented interfaces.
- Verification. The model implementation is verified to really capture the intent of the modeler. No simulations for the actual problem to be solved are carried out for this purpose.
- Initialization. Reasonable initial values are provided or computed, the numerical solution process is debugged.
- Validation. The results of the simulation are validated against some reference, ideally against experimental data.
- Documentation. The modeling process, the model, and the simulation results during validation and application of the model are documented.
- Model application. The model is used in some model-based process engineering problem solving task.
For other model types, like neural network models where data-driven knowledge is utilized, the modeling process will be somewhat different. Some of the tasks like the conceptual modeling phase, will vanish.
Typical application areas for dynamic models are control, prediction, planning, and fault detection and diagnosis. A major deficiency of today's methods is the lack of ability to utilize a wide variety of knowledge. As an example, a black-box model structure has very limited abilities to utilize first principles knowledge on a problem. this has provided a basis for developing different hybrid schemes. Two hybrid schemes will highlight the discussion. First, it will be shown how a mechanistic model can be combined with a black-box model to represent a pH neutralization system efficiently. Second, the combination of continuous and discrete control inputs is considered, utilizing a two-tank example as case. Different approaches to handle this heterogeneous case are considered.
The hybrid approach may be viewed as a means to integrate different types of knowledge, i.e., being able to utilize a heterogeneous knowledge base to derive a model. Standard practice today is that almost any methods and software can treat large homogeneous data-sets. A typical example of a homogeneous data-set is time-series data from some system, e.g., temperature, pressure, and compositions measurements over some time frame provided by the instrumentation and control system of a chemical reactor. If textual information of a qualitative nature is provided by plant personnel, the data becomes heterogeneous.
The above discussion will form the basis for analyzing the interaction between knowledge discovery, and modeling and identification of dynamic models. In particular, we will be interested in identifying how concepts from knowledge discovery can enrich state-of-the- art within control, prediction, planning, and fault detection and diagnosis of dynamic systems.
Further Readings:
Marco D., Building and Managing the Meta Data Repository: A Full Lifecycle Guide, John Wiley, 2000.
Thuraisingham B., Data Mining: Technologies, Techniques, Tools, and Trends, CRC Press, 1998.
Westphal Ch., T. Blaxton, Data Mining Solutions: Methods and Tools for Solving Real-World Problems, John Wiley, 1998.
Neural Networks Applications
Artificial neural networks provide a well-established, powerful tool to infer patterns from large databases. They have proven to be very useful to solve problems of interpolation, classification and prediction, and have been used in a vast number of business and financial applications.The classical approaches are the feedforward neural networks, trained using back-propagation, which remain the most widespread and efficient technique to implement supervised learning. The main steps are: preprocess the data, the appropriate selection of variables, postprocessing of the results, and a final validation of the global strategy. Applications include data mining, and stock market predictions.
Further Readings:
Schurmann J., Pattern Classification: A Unified View of Statistical and Neural Approaches, John Wiley & Sons, 1996.
Bayes and Empirical Bayes Methods
Bayes and empirical Bayes (EB) methods structure combining information from similar components of information and produce efficient inferences for both individual components and shared model characteristics. Many complex applied investigations are ideal settings for this type of synthesis. For example, county-specific disease incidence rates can be unstable due to small populations or low rates. 'Borrowing information' from adjacent counties by partial pooling produces better estimates for each county, and Bayes/empirical Bayes methods structure the approach. Importantly, recent advances in computing and the consequent ability to evaluate complex models, have increase the popularity and applicability of Bayesian methods.Bayes and EB methods can be implemented using modern Markov chain Monte Carlo(MCMC) computational methods. Properly structured Bayes and EB procedures typically have good frequentist and Bayesian performance, both in theory and in practice. This in turn motivates their use in advanced high-dimensional model settings (e.g., longitudinal data or spatio-temporal mapping models), where a Bayesian model implemented via MCMC often provides the only feasible approach that incorporates all relevant model features.
Further Readings:
Bernardo J., and A. Smith, Bayesian Theory, Wiley, 2000.
Carlin B., and T. Louis, Bayes and Empirical Bayes Methods for Data Analysis, Chapman and Hall, 1996.
Congdon P., Bayesian Statistical Modelling, Wiley, 2001.
Press S., and J. Tanur, The Subjectivity of Scientists and the Bayesian Approach, Wiley, 2001. Comparing and contrasting the reality of subjectivity in the work of history's great scientists and the modern Bayesian approach to statistical analysis.
Markovian & Memory Theory
According to the Memory (M) Theory, in modeling the memory events, events that depend on two or more past times, not just 1 as in Markov chains/processes, or none as in time-independent events, it is best to change ratios to differences (plus a constant - 1 is very nice, but other constants including 0 are often used). Ratios and products work best in Bayesian Markov chains and processes. Differences (subtraction) and sums work best in M Theory and M Events. These latter events range from viscoelastic materials through human memory to economic/financial/biological memory processes. Addition and subtraction has its own simplifications (e.g., geometric series sum exceptionally easily), and at an advanced level a special type of multiplication generalizes subtraction, namely the convolution product which is already widely recognized as being involved in memory (via Volterra integral and integral-differential equations, etc.). Volterra equations, by the way, are relatively easy to solve, and even numerical analysis/approximation software is just as available as main software if you know where to look (usually in the physical science/engineering software). The simplification due to convolution products is at least as great as the simplification involved in multiplicative ordinary multiplication, and allows advanced Fourier transform and Laplace transform methods to be used.Memory Theory and time series share the additive property and inside a single term there can be multiplication, but like general regression methods this does not always mean that they are all using M Theory. One may use standard time series methods in the initial phase of modeling things, but instead proceed as follows using M Theory's Cross-Term Dimensional Analysis (CTDA). Suppose that you postulate a model y = af(x) - bg(z) + ch(u) where f, g, h are some functions and x, z, u are what are usually referred to as independent variables. Notice the minus sign (-) to the left of b and the + sign to the left of c and (implicitly) to the left of a, where a, b, c are positive constants. The variable y is usually referred to as a dependent variable. According to M Theory, not only do f, g, and h influence/cause y, but g influences/causes f and h at least to some extent. In fact, M Theory can formulate this in terms of probable influence as well as deterministic influence. All this generalizes to the case where the functions f, g, h depend on two or more variables, e.g., f(x, w), g(z, t, r), etc.
One can reverse this process. If one thinks that f influences g and h and y but that h and g only influence y and not f, then express the equation of y in the above form. If it works, one has found something that mainstream regression and time series may fail to detect. Of course, path analysis and Lisrel and partial least squares also claim to have ‘causal' abilities, but only in the standard regression sense of ‘freezing' so-called independent variables as ‘givens' and not in the M Theory sense which allows them to vary with y. In fact, Bayesian probability/statistics methods and M Theory methods use respectively ratios like y/x and differences like y - x + 1 in their equations, and in the Bayesian model x is fixed but in the M Theory model x can vary. If one looks carefully, one will notice that the Bayesian model blows up at x = 0 (because division by 0 is impossible, visit the The Zero Saga page), but also near x = 0 since an artificially enormous increase is introduced - precisely near rare events. That is one of the reasons why M Theory is more successful for rare and/or highly influenced/influencing events, while Bayesian and mainstream methods work fairly well for frequent/common and/or low influence (even independent) and/or low dependence events.
Further Readings:
Kursunuglu B., S. Mintz, and A. Perlmutter, Quantum Gravity, Generalized Theory of Gravitation, and Superstring Theory-Based Unification, Kluwer Academic/Plenum, New York 2000.
Likelihood Methods
Direct Inverse
_______________________________________________
Neyman-Pearson Bayesian (decision analysis)
Decision Wald (H. Rubin, e.g.)
--------------------------------------------------------------
Hybrid "Standard" practice Bayesian (subjective)
------------------------------------------------------------------
fiducial (Fisher)
Inference Early Fisher likelihood (Edwards)
Bayesian (modern)
belief functions (Shafer)
____________________________________________________________________
In the Direct schools, one uses Pr(data | hypothesis), usually from some model-based sampling distribution, but one does not attempt to give the inverse probability, Pr(hypothesis | data), nor any other quantitative evaluation of hypotheses. The Inverse schools do associate numerical values with hypotheses, either probabilities (Bayesian schools) or something else (Fisher, Edwards, Shafer).
The decision-oriented methods treat statistics as a matter of action, rather than inference, and attempt to take utilities as well as probabilities into account in selecting actions; the inference-oriented methods treat inference as a goal apart from any action to be taken.
The "hybrid" row could be more properly labeled as "hypocritical"-- these methods talk some Decision talk but walk the Inference walk.
Fisher's fiducial method is included because it is so famous, but the modern consensus is that it lacks justification.
Now it is true, under certain assumptions, some distinct schools advocate highly similar calculations, and just talk about them or justify them differently. Some seem to think this is tiresome or impractical. One may disagree, for three reasons:
First, how one justifies calculations goes to the heart of what the calculations actually MEAN; second, it is easier to teach things that actually make sense (which is one reason that standard practice is hard to teach); and third, methods that do coincide or nearly so for some problems may diverge sharply for others.
The difficulty with the subjective Bayesian approach is that prior knowledge is represented by a probability distribution, and this is more of a commitment than warranted under conditions of partial ignorance. (Uniform or improper priors are just as bad in some respects as anything other sort of prior.) The methods in the (Inference, Inverse) cell all attempt to escape this difficulty by presenting alternative representations of partial ignorance.
Edwards, in particular, uses logarithm of normalized likelihood as a measure of support for a hypothesis. Prior information can be included in the form of a prior support (log likelihood) function; a flat support represents complete prior ignorance.
One place where likelihood methods would deviate sharply from "standard" practice is in a comparison between a sharp and a diffuse hypothesis. Consider H0: X ~ N(0, 100) [diffuse] and H1: X ~ N(1, 1) [standard deviation 10 times smaller]. In standard methods, observing X = 2 would be undiagnostic, since it is not in a sensible tail rejection interval (or region) for either hypothesis. But while X = 2 is not inconsistent with H0, it is much better explained by H1--the likelihood ratio is about 6.2 in favor of H1. In Edwards' methods, H1 would have higher support than H0, by the amount log(6.2) = 1.8. (If these were the only two hypotheses, the Neyman-Pearson lemma would also lead one to a test based on likelihood ratio, but Edwards' methods are more broadly applicable.)
I do not want to appear to advocate likelihood methods. I could give a long discussion of their limitations and of alternatives that share some of their advantages but avoid their limitations. But it is definitely a mistake to dismiss such methods lightly. They are practical (currently widely used in genetics) and are based on a careful and profound analysis of inference.
What is a Meta-Analysis?
Meta-Analysis deals with the art of combining information from the data from different independent sources which are targeted at a common goal. There are plenty of applications of Meta-Analysis in various disciplines such as Astronomy, Agriculture, Biological and Social Sciences, and Environmental Science. This particular topic of statistics has evolved considerably over the last twenty years with applied as well as theoretical developments.A Meta-analysis deals with a set of RESULTs to give an overall RESULT that is (presumably) comprehensive and valid.
a) Especially when Effect-sizes are rather small, the hope is that one can gain good power by essentially pretending to have the larger N as a valid, combined sample.
b) When effect sizes are rather large, then the extra POWER is not needed for main effects of design: Instead, it theoretically could be possible to look at contrasts between the slight variations in the studies themselves.
If you really trust that "all things being equal" will hold up. The typical "meta" study does not do the tests for homogeneity that should be required
In other words:
1. there is a body of research/data literature that you would like to summarize
2. one gathers together all the admissible examples of this literature (note: some might be discarded for various reasons)
3. certain details of each investigation are deciphered ... most important would be the effect that has or has not been found, i.e., how much larger in sd units is the treatment group's performance compared to one or more controls.
4. call the values in each of the investigations in #3 .. mini effect sizes.
5. across all admissible data sets, you attempt to summarize the overall effect size by forming a set of individual effects ... and using an overall sd as the divisor .. thus yielding essentially an average effect size.
6. in the meta analysis literature ... sometimes these effect sizes are further labeled as small, medium, or large ....
You can look at effect sizes in many different ways .. across different factors and variables. but, in a nutshell, this is what is done.
I recall a case in physics, in which, after a phenomenon had been observed in air, emulsion data was examined. The theory would have about a 9% effect in emulsion, and behold, the published data gave 15%. As it happens, there was no significant (practical, not statistical) in the theory, and also no error in the data. It was just that the results of experiments in which nothing statistically significant was found were not reported.
This non-reporting of such experiments, and often of the specific results which were not statistically significant, which introduces major biases. This is also combined with the totally erroneous attitude of researchers that statistically significant results are the important ones, and than if there is no significance, the effect was not important. We really need to between the term "statistically significant", and the usual word significant.
It is very important to distinction between statistically significant and generally significant, see Discover Magazine (July, 1987), The Case of Falling Nightwatchmen, by Sapolsky. In this article, Sapolsky uses the example to point out the very important distinction between statistically significant and generally significant: A diminution of velocity at impact may be statistically significant, but not of importance to the falling nightwatchman.
Be careful about the word "significant". It has a technical meaning, not a commonsense one. It is NOT automatically synonymous with "important". A person or group can be statistically significantly taller than the average for the population, but still not be a candidate for your basketball team. Whether the difference is substantively (not merely statistically) significant is dependent on the problem which is being studied.
Meta-analysis is a controversial type of literature review in which the results of individual randomized controlled studies are pooled together to try to get an estimate of the effect of the intervention being studied. It increases statistical power and is used to resolve the problem of reports which disagree with each other. It's not easy to do well and there are many inherent problems.
There is also graphical technique to assess robustness of meta-analysis results. We should carry out the meta-analysis dropping consecutively one study, that is if we have N studies we should do N meta-analysis using N-1 studies in each one. After that we plot these N estimates on the y axis and compare them with a straight line that represent the overall estimate using all the studies.
Topics in Meta-analysis includes: Odds ratios; Relative risk; Risk difference; Effect size; Incidence rate difference and ratio; Plots and exact confidence intervals.
Further Readings:
Glass, et al., Meta-Analysis in Social Research, McGraw Hill, 1987
Cooper H., and L. Hedges, (Eds.), Handbook of Research Synthesis, Russell Sage Foundation, New York, 1994
Industrial Data Modeling
Industrial Data Modeling is the application of statistical, mathematical and computing techniques to industrial problems. Its applications aimed at science and engineering practitioners and managers in industry, considers the modeling, analysis and interpretation of data in industries associated with science, engineering and biomedicine. The techniques are closely related to those of chemometrics, technometrics and biometrics.
Further Readings:
Montgomery D., and G. Runger, Applied Statistics and Probability for Engineers, Wiley, 1998.
Ross Sh., Introduction to Probability and Statistics for Engineers and Scientists, Academic Press, 1999.
Prediction Interval
The idea is that if is the mean of a random sample of size n from a normal population, and Y is a single additional observation, then the test statistic
is the mean of a random sample of size n from a normal population, and Y is a single additional observation, then the test statistic  - Y is normal with mean 0 and variance (1 + 1/n)s2.
- Y is normal with mean 0 and variance (1 + 1/n)s2.
Since we don't actually know s2, we need to use t in evaluating the test statistic. The appropriate Prediction Interval for Y is
 ± ta/2.S.(1+1/n)1/2.
± ta/2.S.(1+1/n)1/2.
This is similar to construction of interval for individual prediction in regression analysis.
Fitting Data to a Broken Line
Fitting data to a broken, how to determine the parameters, a, b, c, and d such that
y = a + b x, for x less than or equal c
y = a - d c + (d + b) x, for x greater than or equal to c
A simple solution is a brute force search across the values of c. Once c is known, estimating a, b, and d is trivial through the use of indicator variables. One may use (x-c) as your independent variable, rather than x, for computational convenience.
Now, just fix c at a fine grid of x values in the range of your data, estimate a, b, and d, and then note what the mean squared error is. Select the value of c that minimizes the mean squared error.
Unfortunately, you won't be able to get confidence intervals involving c, and the confidence intervals for the remaining parameters will be conditional on the value of c.
Further Readings:
For more details, see Applied Regression Analysis, by Draper and Smith, Wiley 1981, Chapter 5, section 5.4 on use of dummy variables. example 6.
How to Determine if Two Regression Lines Are Parallel?
Would like to determine if two regression lines are parallel? Construct the following multiple linear regression model:E(y) = b0 + b1X1 + b2X2 + b3X3That is, E(y|group=1) is a simple regression with a potentially different slope and intercept compared to group=0.where X1 = interval predictor variable, X2 = 1 if group 1, 0 if group 0, and X3 = X1.X2 Then, E(y|group=0) = b0 + b1X1 and E(y|group=1) = b0 + b1X1 + b2.1 + b3.X1.1 = b0 + b1.X1 + b2 + b3X1 = (b0 + b2) + (b1 + b3)X1
Ho: slope(group 1) = slope(group 0) is equivalent to Ho: b3=0
Use t-test from variables-in-the equation table to test this hypothesis.
Constrained Regression Model
If you fit a regression forcing the intercept to be zero, the standard error of the slope is less. That seems counter-intuitive. The intercept should be included in the model because it is significant, so why is the standard error for the slope in the worse-fitting model actually smaller?I agree that it's initially counter-intuitive (see below), but here are two reasons why it's true. The variance of the slope estimate for the constrained model is s2 / SXi 2), where Xi are actual X values and s2 is estimated from the residuals. The variance of the slope estimate for the unconstrained model (with intercept) is s2 / Sxi 2), where xi are deviations from the mean, and s2 is still estimated from the residuals). So, the constrained model can have a larger s2 (mean square error/"residual" and standard error of estimate) but a smaller standard error of the slope because the denominator is larger.
r2 also behaves very strangely in the constrained model; by the conventional formula, it can be negative; by the formula used by most computer packages, it is generally larger than the unconstrained r2 because it is dealing with deviations from 0, not deviations from the mean. This is because, in effect, constraining the intercept to 0 forces us to act as if the mean of X and the mean of Y both were 0.
Once you recognize that the s.e. of the slope isn't really a measure of overall fit, the result starts to make a lot of sense. Assume that all your X and Y are positive. If you're forced to fit the regression line through the origin (or any other point) there will be less "wiggle" in how you can fit the line to the data than there would be if both "ends" could move.
Consider a bunch of points that are ALL way out, far from zero, then if you Force the regression through zero, that line will be very close to all the points, and pass through origin, with LITTLE ERROR. And little precision, and little validity. Therefore, no-intercept model is hardly ever appropriate.
Semiparametric and Non-parametric modeling
Many parametric regression models in applied science have a form like response = function(X1,..., Xp, unknown influences). The "response" may be a decision (to buy a certain product), which depends on p measurable variables and an unknown reminder term. In statistics, the model is usually written asY = m( X1, ..., Xp) + e
and the unknown e is interpreted as error term.
The most simple model for this problem is the linear regression model, an often used generalization is the Generalized Linear Model (GLM)
Y= G(X1b1 + ... + Xpbp) + e
where G is called the link function. All these models lead to the problem of estimating a multivariate regression. Parametric regression estimation has the disadvantage, that by the parametric "form" certain properties of the resulting estimate are already implied.
Nonparametric techniques allow diagnostics of the data without this restriction. However, this requires large sample sizes and causes problems in graphical visualization. Semiparametric methods are a compromise between both: they support a nonparametric modeling of certain features and profit from the simplicity of parametric methods.
Further Readings:
Härdle W., S. Klinke, and B. Turlach, XploRe: An Interactive Statistical Computing Environment, Springer, New York, 1995.
Moderation and Mediation
"Moderation" is an interactional concept. That is, a moderator variable "modifies" the relationships between two other variables. While "Mediation" is a "causal modeling" concept. The "effect" of one variable on another is "mediated" through another variable. That is, there is no "direct effect", but rather an "indirect effect."Discriminant and Classification
Classification or discrimination involves learning a rule whereby a new observation can be classified into a pre-defined class. Current approaches can be grouped into three historical strands: statistical, machine learning and neural network. The classical statistical methods make distributional assumptions. There are many others which are distribution free, and which require some regularization so that the rule performs well on unseen data. Recent interest has focused on the ability of classification methods to be generalized.We often need to classify individuals into two or more populations based on a set of observed "discriminating" variables. Methods of classification are used when discriminating variables are:
- quantitative and approximately normally distributed;
- quantitative but possibly nonnormal;
- categorical; or
- a combination of quantitative and categorical.
It is important to know when and how to apply linear and quadratic discriminant analysis, nearest neighbor discriminant analysis, logistic regression, categorical modeling, classification and regression trees, and cluster analysis to solve the classification problem. SAS has all the routines you need to for proper use of these classifications. Relevant topics are: Matrix operations, Fisher's Discriminant Analysis, Nearest Neighbor Discriminant Analysis, Logistic Regression and Categorical Modeling for classification, and Cluster Analysis.
For example, two related methods which are distribution free are the k-nearest neighbor classifier and the kernel density estimation approach. In both methods, there are several problems of importance: the choice of smoothing parameter(s) or k, and choice of appropriate metrics or selection of variables. These problems can be addressed by cross-validation methods, but this is computationally slow. An analysis of the relationship with a neural net approach (LVQ) should yield faster methods.
Further Readings:
Cherkassky V, and F. Mulier, Learning from Data: Concepts, Theory, and Methods, John Wiley & Sons, 1998.
Denison, D., C. Holmes, B. Mallick, and A.Smith, Bayesian Methods for Nonlinear Classification and Regression, Wiley, 2002.
Index of Similarity in Classification
In many natural sciences, such as ecologists one is interested in a notion of similarity. The index of similarity is devised for comparing, e.g., the species diversity between two different samples or communities. Let a be the total number of species in sample1, b is the number of species in sample2, and j is the number of species common to both samples, then the widely used similarity index is the Mountford Index defined as:
A rather computationally involved for determining a similarity index (I) is due to Fisher, where I is the solution to the following equation:
The index of similarity could be used as a "distance" so that the minimum distance corresponds to the maximum similarity.
Further Readings:
Hayek L., and M. Buzas, Surveying Natural Populations, Columbia University Press, NY, 1996.
Generalized Linear and Logistic Models
The generalized linear model (GLM) is possibly the most important development in practical statistical methodology in the last twenty years. Generalized linear models provide a versatile modeling framework in which a function of the mean response is "linked" to the covariates through a linear predictor and in which variability is described by a distribution in the exponential dispersion family. These models include logistic regression and log-linear models for binomial and Poisson counts together with normal, gamma and inverse Gaussian models for continuous responses. Standard techniques for analyzing censored survival data, such as the Cox regression, can also be handled within the GLM framework. Relevant topics are: Normal theory linear models, Inference and diagnostics for GLMs, Binomial regression, Poisson regression, Methods for handling overdispersion, Generalized estimating equations (GEEs).Hre is how to obtain degree of freedom number for the 2 log-likelihood, in a logistic regression. Degrees of freedom pertain to the dimension of the vector of parameters for a given model. Suppose we know that a model ln(p/(1-p))=Bo + B1x + B2y + B3w fits a set of data. In this case the vector B=(Bo,B1, B2, B3) is an element of 4 dimensional Euclidean space, or R4.
Suppose we want to test the hypothesis: Ho: B3=0. We are imposing a restriction on our parameter space. The vector of parameters must be of the form: B'=B=(Bo,B1, B2, 0). This vector is an element of a subspace of R4. Namely, B4=0 or the X-axis. The likelihood ration statistic has the form:
2 log-likelihood = 2 log(maximum unrestricted likelihood / maximum restricted likelihood) =
2 log(maximum unrestricted likelihood)-2 log (maximum restricted likelihood)
Which is unrestricted B vector 4-dimensions or degrees of freedom - restricted B vector 3 dimensions or degrees of freedom = 1 degree of freedom which is the difference vector: B''=B-B'=(0,0,0,B4) [one dimensional subspace of R4.
The standard textbook is Generalized Linear Models by McCullagh and Nelder (Chapman & Hall, 1989).
LOGISTIC REGRESSION VAR=x
/METHOD=ENTER y x1 x2 f1ros f1ach f1grade bylocus byses
/CONTRAST (y)=Indicator
/contrast (x1)=indicator
/contrast (x2)=indicator
/CLASSPLOT /CASEWISE OUTLIER(2)
/PRINT=GOODFIT
/CRITERIA PIN(.05) POUT(.10) ITERATE(20) CUT(.5) .
Other SPSS Commands:
Loglinear LOGLINEAR,HILOGLINEAR Logistic Regression LOGLINEAR,PROBITSAS Commands:
Loglinear CATMOD Logistic Regression LOGISTIC, CATMOD,PROBIT
Further Readings:
Harrell F, Regression Modeling Strategies: With Applications to Linear Models, Logistic
Regression, and Survival Analysis, Springer Verlag, 2001.
Hosmer D. Jr., and S. Lemeshow, Applied Logistic Regression, Wiley, 2000.
Katz M., Multivariable Analysis: A Practical Guide for Clinicians, Cambridge University Press, 1999.
Kleinbaum D., Logistic Regression: A Self-Learning Text, Springer Verlag, 1994.
Pampel F., Logistic Regression: A Primer, Sage, 2000.
Survival Analysis
Survival analysis is suited to the examination of data where the outcome of interest is 'time until a specific event occurs', and where not all individuals have been followed up until the event occurs. Survival data arise in a literal form from trials concerning life-threatening conditions, but the methodology can also be applied to other waiting times such as the duration of pain relief.The methods of survival analysis are applicable not only in studies of patient survival, but also studies examining adverse events in clinical trials, time to discontinuation of treatment, duration in community care before re-hospitalisation, contraceptive and fertility studies etc.
If you've ever used regression analysis on longitudinal event data, you've probably come up against two intractable problems:
Censoring: Nearly every sample contains some cases that do not experience an event. If the dependent variable is the time of the event, what do you do with these "censored" cases?
Time-dependent covariate: Many explanatory variables (like income or blood pressure)change in value over time. How do you put such variables in a regression analysis?
Makeshift solutions to these questions can lead to severe biases. Survival methods are explicitly designed to deal with censoring and time-dependent covariates in a statistically correct way. Originally developed by biostatisticians, these methods have become popular in sociology, demography, psychology, economics, political science, and marketing.
In Short, survival Analysis is a group of statistical methods for analysis and interpretation of survival data. Even though survival analysis can be used in a wide variety of applications (e.g. insurance, engineering, and sociology), the main application is for analyzing clinical trials data. Survival and hazard functions, the methods of estimating parameters and testing hypotheses that are the main part of analyses of survival data. Main topics relevant to survival data analysis are: Survival and hazard functions, Types of censoring, Estimation of survival and hazard functions: the Kaplan-Meier and life table estimators, Simple life tables, Peto's Logrank with trend test and hazard ratios and Wilcoxon test, (can be stratified), Wei-Lachin, Comparison of survival functions: The logrank and Mantel-Haenszel tests, The proportional hazards model: time independent and time dependent covariates, The logistic regression model, and Methods for determining sample sizes.
In the last few years the survival analysis software available in several of the standard statistical packages has experienced a major increment in functionality, and is no longer limited to the triad of Kaplan-Meier curves, logrank tests, and simple Cox models.
Further Readings:
Hosmer D., and S. Lemeshow, Applied Survival Analysis: Regression Modeling of Time to Event Data, Wiley, 1999.
Janssen P., J. Swanepoel, and N. Veraverbeke, The modified bootstrap error process for Kaplan-Meier quantiles, Statistics & Probability Letters, 58, 31-39, 2002.
Kleinbaum D., et al., Survival Analysis: A Self-Learning Text, Springer-Verlag, New York, 1996.
Lee E., Statistical Methods for Survival Data Analysis, Wiley, 1992.
Therneau T., and P. Grambsch, Modeling Survival Data: Extending the Cox Model, Springer 2000. This book provides thorough discussion on Cox PH model. Since the first author is also the author of the survival package in S-PLUS/R, the book can be used closely with the packages in addition to SAS.
Association Among Nominal Variables
There are many measures of association between two dichotomous variables, such as the odds ratio (AD/BC), Yule's Q = (AD-BC/AD+BC) which is a simple mapping of the odds ratio onto [-1,1], the proportional difference (requires treating one of the variables as "independent" and the other "dependent"), Cramer's V, the contingency coefficient C, the uncertainly coefficient, and the relative risk. Some of those measures may be more appropriate than others for a given situation, however, those based on the odds ratio are easier to interpret. Odds ratios can be thought of as the effect of one outcome on another. If condition 1 is true, what effect has it on the odds of condition 2 being true? Almost all of these statistics are described in the Numerical Recipes, by Press et al.Spearman's Correlation, and Kendall's tau Application
How would you compare the values of two variables to determine whether they are ordered the same? For example:
Var1 Var2
Obs 1 x x
Obs 2 y z
Obs 3 z y
Is Var1 ordered the same as Var2? Two measures are Spearman's rank order correlation, and Kendall's tau.
Further Readings:
For more details see, e.g., Fundamental Statistics for the Behavioral Sciences, by David C. Howell, Duxbury Pr., 1995.
Repeated Measures and Longitudinal Data
Repeated measures and longitudinal data require special attention because they involve correlated data that commonly arise when the primary sampling units are measured repeatedly over time or under different conditions. Normal theory models for split-plot experiments and repeated measures ANOVA can be used to introduce the concept of correlated data. PROC GLM and PROC MIXED in the SAS system may be used. Mixed linear models provide a general framework for modeling covariance structures, a critical first step that influences parameter estimation and tests of hypotheses. The primary objectives are to investigate trends over time and how they relate to treatment groups or other covariates. Techniques applicable to non-normal data, such as McNemar's test for binary data, weighted least squares for categorical data, and generalized estimating equations (GEE) are the main topics. The GEE method can be used to accommodate correlation when the means at each time point are modelled using a generalized linear model. Relevant topics are: Balanced split-plot and repeated measures designs, Modeling covariance structures of repeated measures, Repeated measures with unequally spaced times and missing data, Weighted least squares approach to repeated categorical data, Generalized estimating equation (Gee) method for marginal models, Subject-specific versus population averaged interpretation of regression coefficients, and Computer implementation using S-plus and the SAS system. The following describes the McNemar's test for binary data.McNemar Change Test: For the yes/no questions under the two conditions, set up a 2x2 contingency table:
f11 f10 f01 f00McNemar's test of correlated proportions is z = (f01 - f10)/(f01 + f10)½.
For those items yielding a score on a scale, the conventional t-test for correlated samples would be appropriate, or the Wilcoxon signed-ranks test.
What Is a Systematic Review?
Health care decision makers need to access research evidence to make informed decisions on diagnosis, treatment and health care management for both individual patients and populations. Systematic reviews are recognized as one of the most useful and reliable tools to assist this practice of evidence-based health care. These courses aim to train health care professionals and researchers in the science and methods of systematic reviews.
There are few important questions in health care which can be informed by consulting the result of a single empirical study. Systematic reviews attempt to provide answers to such problems by identifying and appraising all available studies within the relevant focus and synthesizing their results, all according to explicit methodologies. The review process places special emphasis on assessing and maximizing the value of data, both in issues of reducing bias and minimizing random error. The systematic review method is most suitably applied to questions of patient treatment and management, although it has also been applied to answer questions
regarding the value of diagnostic test results, likely prognoses and the cost-effectiveness of health care.
Information Theory
Information theory is a branch probability and mathematical statistics that deal with communication systems, data transmission, cryptography, signal to noise ratios, data compression, etc. Claude Shannon is the father of information theory. His theory considered the transmission of information as a statistical phenomenon and gave communications engineers a way to determine the capacity of a communication channel about the common currency of bitsShannon defined a measure of entropy as:
that, when applied to an information source, could determine the capacity of the channel required to transmit the source as encoded binary digits. Shannon's measure of entropy is taken as a measure of the information contained in a message. This is unlike to the portion of the message that is strictly determined (hence predictable) by inherent structures.
Entropy as defined by Shannon is closely related to entropy as defined by physicists in statistical thermodynamics. This work was the inspiration for adopting the term entropy in information theory. Other useful measures of information include mutual information which is a measure of the correlation between two event sets. Mutual information is defined for two events X and Y as:
The field of Information Science has since expanded to cover the full range of techniques and abstract descriptions for the storage, retrieval and transmittal of information.
Incidence and Prevalence Rates
Incidence rate (IR) is the rate at which new events occur in a population. It is defined as: Number of new events in a specified period divided by Number of persons exposed to risk during this periodPrevalence rate (PR) measures the number of cases that are present at a specified period of time. It is defined as: Number of cases present at a specified period of time divides by Number of persons at risk at that specified time.
These two measures are related when considering the average duration (D). That is, PR = IR . D
Note that, for example, county-specific disease incidence rates can be unstable due to small populations or low rates. In epidemiology one can say that IR reflects probability to Become thick at given age, while the PR reflects probability to Be thick at given age.
Other topics in clinical epidemiology include the use of receiver operator curves, and the sensitivity, specificity, predictive value of a test.
Further Readings:
Kleinbaum D., L. Kupper, and K. Muller, Applied Regression Analysis and Other Multivariable Methods, Wadsworth Publishing Company, 1988.
Kleinbaum D., et al., Survival Analysis: A Self-Learning Text, Springer-Verlag, New York, 1996.
Miettinen O., Theoretical Epidemiology, Delmar Publishers, 1986.
Software Selection
The availability of personal computer, computational software, and visual representations of data enables the managers to concentrate on the revealing useful facts from figures. Since the burden of computation has been eliminated, the managers are now able to focus on probing issues and search for creative decision-making under uncertainty. However, you have to be careful when selecting a statistical software. A short list of item for comparison is:
1) Ease of learning,
2) Amount of help incorporated for the user,
3) Level of the user,
4) Number of tests and routines involved,
5) Ease of data entry,
6) Data validation (and if necessary, data locking and security),
7) Accuracy of the tests and routines,
8) Integrated data analysis (graphs and progressive reporting on analysis in one screen),
9) Cost
No one software meets everyone's needs. Determine the needs first and then ask the questions relevant to the above seven criteria.
Spatial Data Analysis
Data that is geographically or spatially referenced is encountered in a very wide variety of practical contexts. In the same way that data collected at different points in time may require specialised analytical techniques, there are a range of statistical methods devoted to the modelling and analysis of data collected at different points in space. Increased public sector and commercial recording and use
of data which is geographically referenced, recent advances in computer hardware and software capable of manipulating and displaying spatial relationships in the form of digital maps, and an awareness of the potential importance of spatial relationships in many areas of research, have all combined to produced an increased interest in spatial analysis. Spatial Data Analysis is concerned with the study of such techniques---the kind of problems they are designed to address, their theoretical justification, when and how to use them in practice.
Many natural phenomena involve a random distribution of points in space. Biologists who observe the locations of cells of a certain type in an organ, astronomers who plot the positions of the stars, botanists who record the positions of plants of a certain species and geologists detecting the distribution of a rare mineral in rock are all observing spatial point patterns in two or three dimensions. Such phenomena can be modelled by spatial point processes.
The spatial linear model is fundamental to a number of techniques used in image processing, for example, for locating gold/ore deposits, or creating maps. There are many unresolved problems in this area such as the behavior of maximum likelihood estimators and predictors, and diagnostic tools. There are strong connections between kriging predictors for the spatial linear model and spline methods of interpolation and smoothing. The two-dimensional version of splines/kriging can be used to construct deformations of the plane, which are of key importance in shape analysis.
For analysis of spatially auto-correlated data in of logistic regression for example, one may use of the Moran Coefficient which is available is some statistical packages such as Spacestat. This statistic tends to be between -1 and +1, though are not restricted to this range. Values near +1 indicate similar values tend to cluster; values near -1 indicate dissimilar values tend to cluster; values near -1/(n-1) indicate values tend to be randomly scattered.
Boundary Line Analysis
The boundary line analysis is dealing with developing the analytical syntheses of real property law, land surveying procedures, & scenario development which helps with decisions for the development of most probable scenarios of boundary location.The main application of this analysis is in the soil electrical conductivity (EC) which stems from the fact that sands have a low conductivity, silts have a medium conductivity and clays have a high conductivity. Consequently, conductivity (measured at low frequencies) correlates strongly to soil grain size and texture.
The boundary line analysis, therefore, is a method of analyzing yield with soil electrical conductivity data. This method isolates the top yielding points for each soil EC range and fits a non-linear line or equation to represent the top-performing yields within each soil EC range. This method knifes through the cloud of EC/Yield data and describes their relationship when other factors are removed or reduced. The upper boundary represents the maximum possible response to that limiting factor, (e.g. EC), and points below the boundary line represents conditions where other factors have limited the response variable. Therefore, one may also use boundary line analysis to compare responses among species.
Further Readings:
Kitchen N., K Sudduth, and S. Drummond, Soil Electrical Conductivity as a Crop Productivity Measure for Claypan Soils, Journal of Production Agriculture, 12(4), 607-617, 1999.
Geostatistics Modeling
The Geostatistics modeling combines the classical statistics-based techniques with space/time imaging. The modeling process includes a group of spatiotemporal concepts and methods that are based on stochastic data analysis. The aim of such modeling approach is to provide a deeper understanding of a theory of knowledge prior to development of mathematical models of scientific mapping and imaging across space and time. One effective approach is the to provides a fundamental insight into the mapping problem in which the knowledge of a natural variable, not the variable itself, is the direct object of study. Several well-known models in this category include the spatiotemporal random fields such as space/time fractals and wavelets which are special cases of the generalized random field modeling.
Further Readings:
Christakos G., Modern Spatiotemporal Geostatistics, Oxford University Press, 2000.
Box-Cox Power Transformation
In certain cases data distribution is not normal (Gaussian), and we wish to find the best transformation of variable in order to obtain a Gaussian data distribution for further statistical processing.Among others the Box-Cox power transformation is often used for this purpose.
y = (xp - 1)/p, for p not zero y = log x, for p = 0trying different values of p between -3 and +3 is usually sufficient but there are MLE methods for estimating the best p. A good source on this and other transformation methods is
Madansky A., Prescriptions for working Statisticians, Springer-Verlag, 1988.
For percentages or proportions (such as for binomial proportions), Arcsine transformations would work better. The original idea of Arcsin(p½)is to establish variances as equal for all groups. The arcsin transform is derived analytically to be the variance-stabilizing and normalizing transformation. The same
limit theorem also leads to the square root transform for Poisson variables (such as counts) and to the arc hyperbolic tangent (i.e., Fisher's Z) transform for correlation. The Arcsin Test yields a z and the 2x2 contingency test yields a chi-sq. But z2 = chi-sq, for large sample size. A good source is
Rao C., Linear Statistical Inference and Its Applications, Wiley, 1973.
How to normalize a set of data consisting of negative and positive values, and make them positive between the range 0.0 to 1.0? Define XNew = (X-min)/(max-min).
Box & Cox power transformation is also very effective for a wide variety of nonnormality:
y(transformed) = yl
where l ranges (in practice) from -3.0 to +3.0. As such it includes, inverse, square root, logarithm, etc. Note that as l approaches 0, one gets a log transformation.
Multiple Comparison Tests
Duncan's multiple-range test: This is one of the many multiple comparison procedures. It is based on the standardized range statistic by comparing all pairs of means while controlling the overall Type I error at a desirable level. While it does not provide interval estimates of the difference between each pair of means, however, it does indicate which means are significantly different from the others. For determining the significant differences between a single control group mean and the other means, one may use the Dunnett's multiple-comparison test.Multiple comparison procedures include topics such as Control of the family-Wise Error rate, The closure Principle, Hierarchical Families of Hypotheses, Single-Step and Stepwise Procedures, and P-value Adjustments. Areas of applications include multiple comparisons among treatment means, multiple endpoints in clinical trials, multiple sub-group comparisons, etc.
Nemenyi's multiple comparison test is analogous to Tukey's test, using rank sums in place of means and using [n2k(nk+1)/12]½ as the estimate of standard error (SE), where n is the size of each sample and k is the number of samples (means). Similarly to the Tukey test, you compare (rank sum A - rank sum B)/SE to the studentized range for k. It is also equivalent to the Dunn/Miller test which uses mean ranks and standard error [k(nk+1)/12]½.
Multilevel Statistical Modeling: The two widely used software packages are MLwiN and winBUGS. They perform multilevel modeling analysis and analysis of hierarchical datasets, Markov chain Monte Carlo (MCMC) methodology and Bayesian approaches.
Further Readings:
Liao T., Statistical Group Comparison, Wiley, 2002.
Antedependent Modeling for Repeated Measurements
Repeated measures data arise when observations are taken on each experimental unit on a number of occasions, and time is a factor of interest.
Many techniques can be used to analyze such data. Antedependence modeling is a recently developed method which models the correlation between observations at different times.
Split-half Analysis
What is split-half analysis? Split your sample in half. Factor analyses each half. Do they come out the same (or similar) as each other? Alternatively (or also), take more than two 2 random subsample of your sample and do the same.Notice that this is (like factor analysis itself) an "exploratory", not inferential technique, i.e. hypothesis testing, confidence intervals etc. simply do not apply.
Alternatively, randomly split the sample in half and then do an exploratory factor analysis on Sample 1. Use those results to do a confirmatory factor analysis with Sample 2.
Sequential Acceptance Sampling
Acceptance sampling is a quality control procedure used when a decision on the acceptability of the batch has to be made from tests done on a sample of items from the batch.Sequential acceptance sampling minimizes the number of items tested when the early results show that the batch clearly meets, or fails to meet, the required standards.
The procedure has the advantage of requiring fewer observations, on average, than fixed sample size tests for a similar degree of accuracy.
Local Influence
Cook's distance measures the effect of removing a single observation on regression estimates. This can be viewed as giving an observation a weight of either zero or one: local influence allows this weight to be small but non-zero.
Cook defined local influence in 1986, and made some suggestions on how to use or interpret it; various slight variations have been defined since then. But problems associated with its use have been pointed out by a number of workers since the very beginning.
Variogram Analysis
Variables are often measured at different locations. The patterns in these spatial variables may be extrapolated by variogram analysis.
A variogram summarizes the relationship between the variance of the difference in pairs of measurements and the distance of the corresponding points from each other.
Credit Scoring: Consumer Credit Assessment
Credit Scoring is now in widespread use across the retail credit industry. At its simplest, a credit scorecard is a model usually statistical, but in use it is embedded in a computer and or human process.Accurate assessment of financial exposure is vital for continued business success. Accurate, and usable information are essential for good credit assessment in commercial decision making. The consumer credit environment is in a state of great change, driven by developments in computer technology, more demanding customers, availability of new products and increased competition. Banks and other financial institutions are coming to rely more and more on increasingly sophisticated mathematical and statistical tools. These tools are used in a wide range of situations, including predicting default risk, estimating likely profitability, fraud detection, market segmentation, and portfolio analysis. The credit card market as an example, has changed the retail banking industry, and consumer loans.
Both the tools, the behavioral scoring, and the characteristics of consumer credit data are usually the bases for a good decision. The statistical tools include linear and logistic regression, mathematical programming, trees, nearest neighbor methods, stochastic process models, statistical market segmentation, and neural networks. These techniques are used to assess and predict consumers credit scoring.
Further Readings:
Lewis E., Introduction to Credit Scoring, Fair, Isaac & Co., 1994. Provides a general introduction to the issues of building a credit scoring model.
Components of the Interest Rates
The interest rates as quoted in the newspapers and by banks consist of several components. The most important three are:The pure rate: This is the time value of money. A promise of 100 units next year is not worth 100 units this year.
The price-premium factor: If prices go up 5% each year, interest rates go up at least 5%. For example, under the Carter Administration, prices rose about 15% per year for a couple of years, interest was around 25%. Same thing during the Civil War. In a deflationary period, prices may drop so this term can be negative.
The risk factor: A junk bond may pay a larger rate than a treasury note because of the chance of losing the principal. Banks in a poor financial condition must pay higher rates to attract depositors for the same reason. Threat of confiscation by the government leads to high rates in some countries.
Other factors are generally minor. Of course, the customer sees only the sum of these terms. These components fluctuate at different rates themselves. This makes it hard to compare interest rates across disparate time periods or economic condition. The main questions are: how are these components combined to form the index? A simple sum? A weighted sum? In most cases the index is form both empirically and assigned on basis of some criterion of importance. The same applies to other index numbers.
Partial Least Squares
Partial Least Squares (PLS) regression is a multivariate data analysis technique which can be used to relate several response (Y) variables to several explanatory (X) variables.
The method aims to identify the underlying factors, or linear combination of the X variables, which best model the Y dependent variables.
Growth Curve Modeling
Growth is a fundamental property of biological systems, occurring at the level of populations, individual animals and plants, and within organisms. Much research has been devoted to modeling growth processes, and there are many ways of doing this: mechanistic models, time series, stochastic differential equations etc.Sometimes we simply wish to summarize growth observations in terms of a few parameters, perhaps in order to compare individuals or groups. Many growth phenomena in nature show an "S" shaped pattern, with initially slow growth speeding up before slowing down to approach a limit.
These patterns can be modelled using several mathematical functions such as generalized logistic and Gompertz curves.
Saturated Model & Saturated Log Likelihood
A saturated model is usually one that has no residual df. What is a "saturated" log likelihood? So the "saturated LL" is the LL for a saturated model. It is often used when comparisons made between the log likelihood with an intercept only and the log likelihood for a particular model specification.Pattern recognition and Classification
Pattern recognition and classification are fundamental concepts for understanding living systems and essential for realizing artificial intelligent systems. Applications include 3D modelling, motion analysis, feature extraction, device positioning and calibration, feature recognition, solutions to classification problems to industrial and medical applications.What is Biostatistics?
Biostatistics is a subdiscipline of Statistics which focuses on statistical support for the areas of medicine, environmental science, public health, and related fields. Practitioners span the range from the very applied to the very theoretical. The information which is useful to the biostatistician spans the range from that needed by a general statistician, to more subject-specific scientific details, to ordinary information that will improve communication between the biostatistician and other scientists and researchers.Recent advancement in human genome marks a major step in the advancement of understanding how the human body works at a molecular level. The biomedical statistics identifies the need for computational statistical tools to meet important challenges in biomedical studies. The active areas are:
- Clustering of very large dimensional data such as the micro-array.
- Clustering algorithms that support biological meaning.
- Network models and simulations of biological pathways.
- Pathway estimation from data.
- Integration of multi-format and multi-type data from heterogeneous databases.
- Information and knowledge visualization techniques for biological systems.
Further Reading:
Cleophas T., A. Zwinderman, and T. Cleophas, Statistics Applied to Clinical Trials, Kluwer Academic Publishers, 2002.
Zhang W., and I. Shmulevich, Computational and Statistical Approaches to Genomics, Kluwer Academic Publishers, 2002.
Evidential Statistics
Statistical methods aim to answer a variety of questions about observations. A simple example occurs when a fairly reliable test for a condition C, has given a positive result. Three important types of questions are:
1. Should this observation lead me to believe that condition C is present?
2. Does this observation justify my acting as if condition C were present?
3. Is this observation evidence that condition C is present?
We must distinguish among these three questions in terms of the variables and principles that determine their answers. Questions of the third type, concerning the "evidential interpretation" of statistical data, are central to many applications of statistics in many fields.
It is already recognized that for answering the evidential question current statistical methods are seriously flawed which could be corrected by a applying the the Law of Likelihood. This law suggests how the dominant statistical paradigm can be altered so as to generate appropriate methods for objective, quantitative representation of the evidence embodied in a specific set of observations, as well as measurement and control of the probabilities that a study will produce weak or misleading evidence.
Further Reading:
Royall R., Statistical Evidence: A Likelihood Paradigm, Chapman & Hall, 1997.
Statistical Forensic Applications
Cases abound about the role if evidence and inference in constructing and testing arguments and this can be best seen in police and lawyer training where there has been little if any formal instruction on the structural and temporal elements of evidential reasoning. However, little sign exists of methodological approaches to organising evidence and thought as well as a lack of awareness of the benefits such an approach can bring. In addition, there is little regard for the way in which evidence has to be discovered, analyzed and presented as part of a reasoned chain or argument.One consequence of the failure to recognize the benefits that an organized approach can bring is our failure to move evidence as a discipline into volume case analytics. Any cursory view of the literature reveals that work has centered on thinking about single cases using narrowly defined views of what evidential reasoning involves. There has been an over emphasis on the formal rules of admissibility rather than the rules and principles of a methodological scientific approach.
As the popularity of using DNA evidence increases, both the public and professionals increasingly regard it as the last word on a suspect's guilt or innocence. As citizens go about their daily lives, pieces of their identities are scattered in their wake. It could as some critics warn, one day place an innocent person at the scene of a crime.
The traditional methods of statistical forensic, for example, for facial reconstruction date back to the Victorian Era. Tissue depth data was collected from cadavers at a small number of landmark sites on the face. Samples were tiny, commonly numbering less than ten. Although these data sets have been superceded recently by tissue depths collected from the living using ultrasound, the same twenty-or-so landmarks are used and samples are still small and under-representative of the general population. A number of aspects of identity--such as age, height, geographic ancestry and even sex--can only be estimated from the skull. Current research is directed at the recovery of volume tissue depth data from magnetic resonance imaging scans of the head of living individuals; and the development of simple interpolation simulation models of obesity, ageing and geographic ancestry in facial reconstruction.
Further Reading:
Gastwirth J., (Ed.), Statistical Science in the Courtroom, Springer Verlag, 2000.
Spatial Statistics
Many natural phenomena involve a random distribution of points in space. Biologists who observe the locations of cells of a certain type in an organ, astronomers who plot the positions of the stars, botanists who record the positions of plants of a certain species and geologists detecting the distribution of a rare mineral in rock are all observing spatial point patterns in two or three dimensions. Such phenomena can be modelled by spatial point processes.
Further Readings:
Diggle P., The Statistical Analysis of Spatial Point Patterns, Academic Press, 1983.
Ripley B., Spatial Statistics, Wiley, 1981.
What Is the Black-Sholes Model?
The benchmark theory of statistical model for option pricing derivative and evaluation is the Black-Sholes-Merton theory (the Black-Sholes model is a special case which is the limiting distribution of the binomial model), based on Brownian motion as the driving noise process for stock prices. In this model the distributions of financial returns of the stocks in a portfolio are multivariate normal. There are certain limitations in this model, which are, e.g., symmetry and thin tails, which are not the characteristics of the real data. The One may use the Barndorff-Nielsen generalized hyperbolic family, which includes the normal variance-mean mixtures instead of pure multivariate normal.
Further Readings:
Clewlow L., and C. Strickland, Implementing Derivatives Models, John Wiley & Sons, 1998.
What Is a Classification Tree
Basically for each variable, all values are checked and a measure of purity calculated, i.e., loosely the number of classification errors is quantified. The value and variable with lowest split is chosen as the node. This process can then be repeated until all distinct combination of values of independent values have been found. Unfortunately the resulting tree over-fits the data, and would not be vary good for new data sets.There are several methods of deciding when to stop. The simplest method is to split the data into two samples. A tree is developed with one sample and tested with another. The mis-classification rate is calculated by fitting the tree to the test data set and increasing the number of branches one at a time . As the number of nodes used changes the mis-classification rate changes. The number of nodes which minimize the mis-classification rate is chosen.
Graphical Tools for High-Dimensional Classification: Statistical algorithmic classification methods include techniques such as trees, forests, and neural nets. Such methods tend to share two common traits. They can often have far greater predictive power than the classical model-based methods. And they are frequently so complex as to make interpretation very difficult, often resulting in a "black box" appearance. An alternative approach is using graphical tool to facilitate investigation of the inner workings of such classifiers. The A generalization of the ideas such as the data image, and the color histogram allows simultaneous examination of dozens to hundreds of variables across similar numbers of observations. Additional information can be visually incorporated as to true class, predicted class, and casewise variable importance. Careful choice of orderings across cases and variables can clearly indicate clusters, irrelevant or redundant variables, and other features of the classifier, leading to substantial improvements in classifier interpretability.
The various programs vary in how they operate. For making splits, most programs use definition of purity. More sophisticated methods of finding the stopping rule have been developed and depend on the software package.
What Is a Regression Tree
A regression tree is like a classification tree, only with a continuous target (dependent) variable. Prediction of target value for a particular case is made by assigning that case to a node (based on values for the predictor variables) and then predicting the value of the case as the mean of its node (sometimes adjusted for priors, costs, etc.).The Tree-based models known also as recursive partitioning have been used in both statistics and machine learning. Most of their applications to date have, however, been in the fields of regression, classification, and density estimation.
S-PLUS statistical package includes some nice features such as non-parametric regression and tree-based models.
Further Readings:
Breiman L., J. Friedman, R. Olshen and C. Stone, Classification and Regression Trees, CRC Press, Inc., Boca Raton, Florida, 1984.
Cluster Analysis for Correlated Variables
The purpose of Cluster sampling is typically to:- characterize a specific group of interest,
- compare two or more specific groups,
- discover a pattern among several variables.
Cluster analysis is used to classify observations with respect to a set of variables. The widely used Ward's method is predisposed to find spherical clusters and may perform badly with very ellipsoidal clusters generated by highly correlated variables (within clusters).
To deal with high correlations, some model-based methods are implemented in the S-Plus package. However, a limitation of their approach is the need to assume the clusters have a multivariate normal distribution, as well as the need to decide in advance what the likely covariance structure of the clusters is.
Another option is to combine the principal component analysis with cluster analysis.
Further Readings:
Baxter M., Exploratory Multivariate Analysis in Archaeology, pp. 167-170, Edinburgh University Press, Edinburgh, 1994.
Manly F., Multivariate Statistical Methods: A Primer, Chapman and Hall, London, 1986.
Capture-Recapture Methods
Capture-recapture methods were originally developed in the wildlife biology to estimate the population size of some species of wild animals.Tchebysheff Inequality and Its Improvements
The Tchebysheff's inequality is often used to put bounds on the probability that proportion of random variable X will be within k > 1 standard deviation of the mean mu for any probability distribution. In other words:
The symmetric property of Tchebysheff's inequality is useful, e.g., in constructing control limits is the quality control process. However the limits are very conservative because of lack of knowledge about the underlying distribution. This bounds can be improved (i.e., becomes tighter) if we have some knowledge about the population distribution. For example, if the population is homogeneous, that is its distribution is unimodal, then,
The above inequality is known as the Camp-Meidell inequality.
Further Readings:
Efron B., and R. Tibshirani, An Introduction to the Bootstrap, Chapman & Hall (now the CRC Press), 1994. Contains a test for multimodality that is based on the Gaussian kernel density estimates and then test for multimodality by using the window size approach.
Grant E., and R. Leavenworth, Statistical Quality Control, McGraw-Hill, 1996.
Ryan T., Statistical Methods for Quality Improvement, John Wiley & Sons, 2000. A very good book for a starter.
Frechet Bounds for Dependent Random Variables
The simplest form of the Frechet bounds for two dependent random variables A and B with known marginal probability P(A), and P(B), respectively is:
Frechet Bounds is often used in stochastic processes with the effect of dependencies, such as estimating an upper and/or a lower bound on the queue length in a queuing system with two different but known marginal inter-arrivals times distributions of two types of customers.
Statistical Data Analysis in Criminal Justice
This topic usually refers to the wide range of statistics used in the criminal justice system. For example, statistical analysis of the issue of how much crime is drug-related by using the available criminal justice databases, and other source of data. The main issue for the statisticians is to access the specific unit record files for secondary analysis and the long-term implications for evidence based policy making. These analyses must be carried out usually within the specific criminal justice system considering the existence of limitations such as the ethical norms on data release and legislation on privacy and confidentiality.
Further Readings:
McKean J., and Bryan Byers, Data Analysis for Criminal Justice and Criminology, Allyn & Bacon, 2000.
Walker J., Statistics in Criminal Justice: Analysis and Interpretation, Aspen Publishers, Inc., 1999.
What is Intelligent Numerical Computation?
There exist a few computer algebra program software in the market that solve several numerical problem types, which can not be solved by using the ordinary numerical methods. The technique mostly used is to transform the problems, which are difficult to be solved through the ordinary methods, to equivalent problems but are easy to be solved, by defining measure functions that assess the suitable method for every type of problems. The aim of such software is to make the students able to use this package, rather than writing their own programs in any other programming languages.
Software Engineering by Project Management
Software Engineering by Project management Techniques aims at the capital risks on projects to be evaluated, and calculates the financial contingency required to cover those risks in a rational and defensible manner to make bug-free software in a systematic approach. Too often the project contingency is guesstimated as a "gut feel" amount, without much consideration for the real risks involved. The technique enables disciplined estimating, and calculates the required contingency using the proven statistical method known such as Monte Carlo experimentation.The software project scheduling and tracking is to create a network of software engineering tasks that will enable you to get the job done on time. Once the network is created, you have to assign responsibility for each task, make sure it gets done, and adapt the network as risks become reality.
Further Readings:
Ricketts I., Managing Your Software Project: A Student's Guide, London, Springer, 1998.
Chi-Square Analysis for Categorical Grouped Data
Suppose you have the summary data for each categories rather than raw data, and you wish to perform the Chi-Square test, that is when one only has the cell data, not the data from each individual. As a numerical example, consider the following data set:
| Group | Yes | Uncertain | No | |
|---|---|---|---|---|
| 1 | 10 | 21 | 23 | |
| 2 | 12 | 15 | 18 |
One may first construct an equivalent alternative categorical table as follows:
| Group | Reply | Count | |
|---|---|---|---|
| 1 | Y | 10 | |
| 1 | U | 21 | |
| 1 | N | 23 | |
| 2 | Y | 12 | |
| 2 | U | 15 | |
| 2 | N | 18 |
Now, weight the data by counts and then perform the Chi-Square analysis.
Further Reading:
Agresti A., Categorical Data Analysis, Wiley, 2002.
Kish R., G. Kalton, S. Heeringa, C. O'Muircheartaigh, and J. Lepkowski, Collected Papers of Leslie Kish, Wiley, 2002.
Cohen's Kappa: A Measures of Data Consistency
Cohen's kappa measures the agreement internal consistency based on a contingency table. In this context a measure of agreement assesses the extent to which two raters give the same ratings to the same objects. The set of possible values for one rater forms the columns and the same set of possible values for some second rater forms the rows.
Where "by chance" is calculated as in chi-square: multiply row marginal times column marginal and divide by n.
One may use this measure as a decision-making tool:
| k < 0.00 | Poor |
| 0.00 £ k < 0.20 | Slight |
| 0.20 £ k < 0.40 | Fair |
| 0.40 £ k < 0.60 | Moderate |
| 0.60 £ k < 0.80 | Substantial |
| 0.80 £ k | Almost Perfect |
This interpretation is widely accepted, and many scientific journals routinely publish papers using this interpretation for the result of test of hypothesis.
Further Reading:
Looney S., Biostatistical Methods, (ed.), Humana Press, 2002.
Rust R., and B. Cooil, Reliability measures for qualitative data: Theory and implications, Journal of Marketing Research, 31(1), 1-14, 1994.
Modeling Dependent Categorical Data
One may apply regression models to the categorical dependent variables. However, due to the non-linearities of these models the statistical analysis and interpretation of these models is not an easy task. still difficult The most premising approach is via the method of maximum likelihood estimation in developing the logit and probit models for binary and ordinal data. The multinomial logit model is often used for nominal data. An extensions of modeling for count data, includes modeling process for Poisson regression, negative binomial regression, and the zero modified models.
Further Readings:
Agresti A., An Introduction to Categorical Data Analysis, Wiley, 1996.
The Deming Paradigm
While the common practice of Quality Assurance aims to prevent bad units from being shipped beyond some allowable proportion, Statistical Process Control (SPC) ensures that bad units are not created in the first place. Its philosophy of continuous quality improvement, to a great extent responsible for the success of Japanese manufacturing, is rooted in a paradigm as process-oriented as physics, yet produces a friendly and fulfilling work environment.
Further Reading:
Thompson J., and J. Koronacki, Statistical Process Control: The Deming Paradigm and Beyond, CRC Press, 2001.
Reliability & Repairable System
Reliability modeling uses subjective judgements to construct models at many different levels. One area is in the construction of joint probability distributions for the lifetime of several pieces of equipment, or for the failure times due to different failure modes of a single piece of equipment. When there is good reason to believe given marginal distributions for the failure times, the problem of selecting a marginal distribution is equivalent to that of selecting a copula. In other situations identification of the copula alone is important, for example in competing risk where the copula together with competing risk data enable identification of the full joint distribution.The primary intent of reliability engineering is to improve reliability, and almost all systems of interest to reliability engineers are designed to be repairable, this is the most important reliability concept. It is also the simplest, in sharp contrast, spacing between order statistics of the times to failure of non-repairable items (i.e., parts) eventually become stochastically larger. Even under any physically plausible model of wearout. Moreover, if parts are put on test simultaneously and operated continuously, the spacing between order statistics, which are times between failures, occur exactly in calendar time. Because of non-zero repair times, this is never exactly true for a repairable system. As long as a system is non-repairable, the focus usually should be on the underlying distribution's hazard function. Correspondingly, if it is repairable, the focus usually should be on the underlying process's intensity function. However, even though hazard and intensity functions can be - and sometimes have to be - represented by the same mathematical function, the differences in interpretation are significantly different.
Further Reading:
Ascher H., and H. Feingold, Repairable Systems Reliability: Modeling, Inference, Misconceptions and Their Causes, Marcel Dekker, 1984.
Computation of Standard Scores
In many areas such as education and psychology, it is often desired to convert test scores (called raw scores) to standard scores (scores in standard units) with a predetermined mean and standard deviation. This may be accomplished as follows:![]()
where m = raw score mean
s = raw score standard deviation
X = raw score
m ¢ = new mean
s ¢ = new standard deviation
Suppose a population of psychological test scores has a mean of 70 and a standard deviation of 8 and it is desired to convert these scores to standard scores with a mean of 100 and a standard deviation of 20. If 40 is one of the raw scores in the population, we may apply the foregoing equation to convert this to a standard score by substituting
m = 70, s = 8, X = 40, m ¢ = 100, s ¢ = 20 to obtain
![]()
Quality Function Deployment (QFD)
A number of activities must be conducted when carrying out QFD. Some of the typical activities are listed as follows:- Analyzing customer requirements.
- Identifying design features.
- Establishing interactions between customer requirements and design features.
- Carrying out competitive benchmarking in technical and/or market terms.
- Analyzing the results and deriving implications.
Further Readings:
Franceschini F., Advanced Quality Function Deployment, St. Lucie Press, 2002.
Event History Analysis
Sometimes data on the exact time of a particular event (or events) are available, for example on a group of patients. Examples of events could include asthma attach; epilepsy attack; myocardial infections; hospital admissions. Often, occurrence (and non-occurrence) of an event is available on a regular basis (e.g., daily) and the data can then be thought of as having a repeated measurements structure. An objective may be to determine whether any concurrent events or measurements have influenced the occurrence of the event of interest. For example, daily pollen counts may influence the risk of asthma attacks; high blood pressure may proceed a myocardial infarction. One may use PROC GENMOD available in SAS for the event history analysis.
Further Readings:
Brown H., and R. Prescott, Applied Mixed Models in Medicine, Wiley, 1999.
Factor Analysis
Factor Analysis is a technique for data reduction that is, explaining the variation in a collection of continuous variables by a smaller number of underlying dimensions (called factors). Common factor analysis can also be used to form index numbers or factor scores by using correlation or covariance matrix. The main problem with factor analysis concept is that it is very subjective in its interpretation of the results.
Further Reading:
Reyment R., and K. Joreskog, Applied Factor Analysis in the Natural Science, Cambridge University Press, 1996. It covers multivariate analysis and applications to environmental fields such as chemistry, paleoecology, sedimentology, geology and marine ecology.
Tabachick B., and L. Fidell, Using Multivariate Statistics, Harper Collins, New York, 1996.
Kinds of Lies: Lies, Damned Lies and Statistics
"There are three kinds of lies -- lies, damned lies, and statistics." quoted in Mark Twain's autobiography.It is already an accepted fact that "Statistical thinking will one day be as necessary for efficient citizenship as the ability to read and write." However it often happens that people manipulating statistics in their own advantage or in advantage of their boss or friend.
The following are some examples as how statistics could be misused in advertising, which can be described as the science of arresting human unintelligence long enough to get money from it. The founder of Revlon says "In factory we make cosmetics; in the store we sell hope."
In most cases, the deception of advertising is achieved by omission: