for Business Administration
Realization of the fact that "Time is Money" in business activities, the dynamic decision technologies presented here, have been a necessary tool for applying to a wide range of managerial decisions successfully where time and money are directly related. In making strategic decisions under uncertainty, we all make forecasts. We may not think that we are forecasting, but our choices will be directed by our anticipation of results of our actions or inactions.
Indecision and delays are the parents of failure. This site is intended to help managers and administrators do a better job of anticipating, and hence a better job of managing uncertainty, by using effective forecasting and other predictive techniques.
To search the site, try Edit | Find in page [Ctrl + f]. Enter a word or phrase in the dialogue box, e.g. "cash flow" or "capital cycle" If the first appearance of the word/phrase is not what you are looking for, try Find Next.
MENU
- Chapter 1: Time-Critical Decision Modeling and Analysis
- Chapter 2: Causal Modeling and Forecasting
- Chapter 3: Smoothing Techniques
- Chapter 4: Box-Jenkins Methodology
- Chapter 5: Filtering Techniques
- Chapter 6: A Summary of Special Models
- Chapter 7: Modeling Financial and Economics Time Series
- Chapter 8: Cost/Benefit Analysis
- Chapter 9: Marketing and Modeling Advertising Campaign
- Chapter 10: Economic Order and Production Quantity Models for Inventory Management
- Chapter 11: Modeling Financial Economics Decisions
- Chapter 12: Learning and the Learning Curve
- Chapter 13: Economics and Financial Ratios and Price Indices
- Chapter 14: JavaScript E-labs Learning Objects
Companion Sites:
- Business Statistics
- Excel For Statistical Data Analysis
- Topics in Statistical Data Analysis
- Computers and Computational Statistics
- Questionnaire Design and Surveys Sampling
- Probabilistic Modeling
- Systems Simulation
- Probability and Statistics Resources
- Success Science
- Leadership Decision Making
- Linear Programming (LP) and Goal-Seeking Strategy
- Linear Optimization Solvers to Download
- Artificial-variable Free LP Solution Algorithms
- Integer Optimization and the Network Models
- Tools for LP Modeling Validation
- The Classical Simplex Method
- Zero-Sum Games with Applications
- Computer-assisted Learning Concepts and Techniques
- Linear Algebra and LP Connections
- From Linear to Nonlinear Optimization with Business Applications
- Construction of the Sensitivity Region for LP Models
- Zero Sagas in Four Dimensions
- Business Keywords and Phrases
- Collection of JavaScript E-labs Learning Objects
- Compendium of Web Site Review
Chapter 1: Time-Critical Decision Modeling and Analysis
- Introduction
- Effective Modeling for Good Decision-Making
- Balancing Success in Business
- Modeling for Forecasting
- Stationary Time Series
- Statistics for Correlated Data
![]()
Chapter 2: Causal Modeling and Forecasting
- Introduction and Summary
- Modeling the Causal Time Series
- How to Do Forecasting by Regression Analysis
- Predictions by Regression
- Planning, Development, and Maintenance of a Linear Model
- Trend Analysis
- Modeling Seasonality and Trend
- Trend Removal and Cyclical Analysis
- Decomposition Analysis
![]()
Chapter 3: Smoothing Techniques
- Introduction
- Moving Averages and Weighted Moving Averages
- Moving Averages with Trends
- Exponential Smoothing Techniques
- Exponenentially Weighted Moving Average
- Holt's Linear Exponential Smoothing Technique
- The Holt-Winters' Forecasting Technique
- Forecasting by the Z-Chart
- Concluding Remarks
![]()
Chapter 4: Box-Jenkins Methodology
![]()
Chapter 5: Filtering Techniques
![]()
Chapter 6: A Summary of Special Modeling Techniques
- Neural Network
- Modeling and Simulation
- Probabilistic Models
- Event History Analysis
- Predicting Market Response
- Prediction Interval for a Random Variable
- Census II Method of Seasonal Analysis
- Delphi Analysis
- System Dynamics Modeling
- Transfer Functions Methodology
- Testing for and Estimation of Multiple Structural Changes
- Combination of Forecasts
- Measuring for Accuracy
![]()
Chapter 7: Modeling Financial and Economics Time Series
- Introduction
- Modeling Financial Time Series and Econometrics
- Econometrics and Time Series Models
- Simultaneous Equations
- Further Readings
![]()
Chapter 8: Cost/Benefit Analysis
![]()
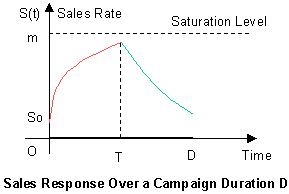
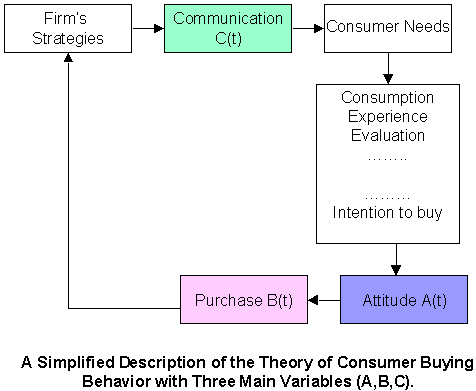
Chapter 9: Marketing and Modeling Advertising Campaign
- Marketing and Modeling Advertising Campaign
- Selling Models
- Buying Models
- The Advertising Pulsing Policy
- Internet Advertising
- Predicting Online Purchasing Behavior
- Concluding Remarks
- Further Readings
![]()
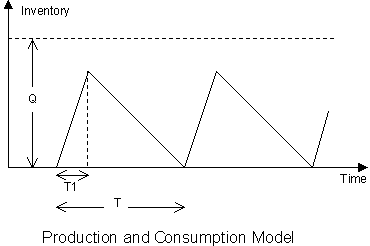
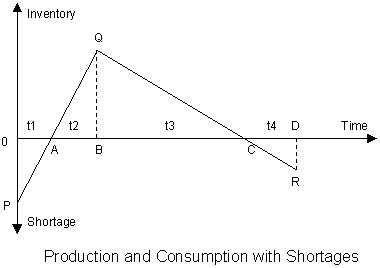
Chapter 10: Economic Order and Production Quantity Models for Inventory Management
- Introduction
- Economic Order and Production Quantity for Inventory Control
- Optimal Order Quantity Discounts
- Finite Planning Horizon Inventory
- Inventory Control with Uncertain Demand
- Managing and Controlling Inventory
![]()
Chapter 11: Modeling Financial Economics Decisions
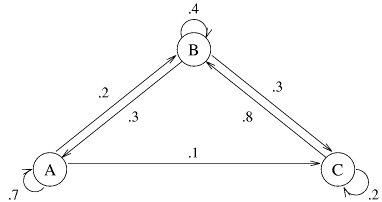
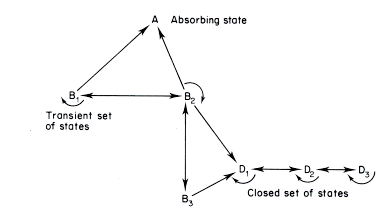
- Markov Chains
- Leontief's Input-Output Model
- Risk as a Measuring Tool and Decision Criterion
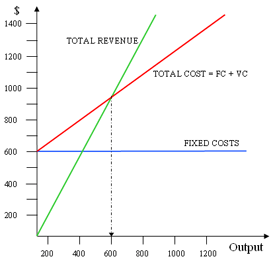
- Break-even and Cost Analyses
- Modeling the Bidding Process
- Products Life Cycle Analysis and Forecasting
![]()
Chapter 12: Learning and The Learning Curve
Time-Critical Decision Modeling and Analysis
The ability to model and perform decision modeling and analysis is an essential feature of many real-world applications ranging from emergency medical treatment in intensive care units to military command and control systems. Existing formalisms and methods of inference have not been effective in real-time applications where tradeoffs between decision quality and computational tractability are essential. In practice, an effective approach to time-critical dynamic decision modeling should provide explicit support for the modeling of temporal processes and for dealing with time-critical situations.One of the most essential elements of being a high-performing manager is the ability to lead effectively one's own life, then to model those leadership skills for employees in the organization. This site comprehensively covers theory and practice of most topics in forecasting and economics. I believe such a comprehensive approach is necessary to fully understand the subject. A central objective of the site is to unify the various forms of business topics to link them closely to each other and to the supporting fields of statistics and economics. Nevertheless, the topics and coverage do reflect choices about what is important to understand for business decision making.
Almost all managerial decisions are based on forecasts. Every decision becomes operational at some point in the future, so it should be based on forecasts of future conditions.
Forecasts are needed throughout an organization -- and they should certainly not be produced by an isolated group of forecasters. Neither is forecasting ever "finished". Forecasts are needed continually, and as time moves on, the impact of the forecasts on actual performance is measured; original forecasts are updated; and decisions are modified, and so on.
For example, many inventory systems cater for uncertain demand. The inventory parameters in these systems require estimates of the demand and forecast error distributions. The two stages of these systems, forecasting and inventory control, are often examined independently. Most studies tend to look at demand forecasting as if this were an end in itself, or at stock control models as if there were no preceding stages of computation. Nevertheless, it is important to understand the interaction between demand forecasting and inventory control since this influences the performance of the inventory system. This integrated process is shown in the following figure:
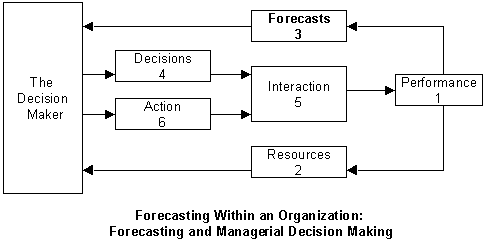
The decision-maker uses forecasting models to assist him or her in decision-making process. The decision-making often uses the modeling process to investigate the impact of different courses of action retrospectively; that is, "as if" the decision has already been made under a course of action. That is why the sequence of steps in the modeling process, in the above figure must be considered in reverse order. For example, the output (which is the result of the action) must be considered first.
It is helpful to break the components of decision making into three groups: Uncontrollable, Controllable, and Resources (that defines the problem situation). As indicated in the above activity chart, the decision-making process has the following components:
- Performance measure (or indicator, or objective): Measuring business performance is the top priority for managers. Management by objective works if you know the objectives. Unfortunately, most business managers do not know explicitly what it is. The development of effective performance measures is seen as increasingly important in almost all organizations. However, the challenges of achieving this in the public and for non-profit sectors are arguably considerable. Performance measure provides the desirable level of outcome, i.e., objective of your decision. Objective is important in identifying the forecasting activity. The following table provides a few examples of performance measures for different levels of management:
Level Performance Measure Strategic Return of Investment, Growth, and Innovations Tactical Cost, Quantity, and Customer satisfaction Operational Target setting, and Conformance with standard Clearly, if you are seeking to improve a system's performance, an operational view is really what you are after. Such a view gets at how a forecasting system really works; for example, by what correlation its past output behaviors have generated. It is essential to understand how a forecast system currently is working if you want to change how it will work in the future. Forecasting activity is an iterative process. It starts with effective and efficient planning and ends in compensation of other forecasts for their performance
What is a System? Systems are formed with parts put together in a particular manner in order to pursue an objective. The relationship between the parts determines what the system does and how it functions as a whole. Therefore, the relationships in a system are often more important than the individual parts. In general, systems that are building blocks for other systems are called subsystems
The Dynamics of a System: A system that does not change is a static system. Many of the business systems are dynamic systems, which mean their states change over time. We refer to the way a system changes over time as the system's behavior. And when the system's development follows a typical pattern, we say the system has a behavior pattern. Whether a system is static or dynamic depends on which time horizon you choose and on which variables you concentrate. The time horizon is the time period within which you study the system. The variables are changeable values on the system.
- Resources: Resources are the constant elements that do not change during the time horizon of the forecast. Resources are the factors that define the decision problem. Strategic decisions usually have longer time horizons than both the Tactical and the Operational decisions.
- Forecasts: Forecasts input come from the decision maker's environment. Uncontrollable inputs must be forecasted or predicted.
- Decisions: Decisions inputs ate the known collection of all possible courses of action you might take.
- Interaction: Interactions among the above decision components are the logical, mathematical functions representing the cause-and-effect relationships among inputs, resources, forecasts, and the outcome.
- Actions: Action is the ultimate decision and is the best course of strategy to achieve the desirable goal.
Interactions are the most important type of relationship involved in the decision-making process. When the outcome of a decision depends on the course of action, we change one or more aspects of the problematic situation with the intention of bringing about a desirable change in some other aspect of it. We succeed if we have knowledge about the interaction among the components of the problem.
There may have also sets of constraints which apply to each of these components. Therefore, they do not need to be treated separately.
Decision-making involves the selection of a course of action (means) in pursue of the decision maker's objective (ends). The way that our course of action affects the outcome of a decision depends on how the forecasts and other inputs are interrelated and how they relate to the outcome.
Controlling the Decision Problem/Opportunity: Few problems in life, once solved, stay that way. Changing conditions tend to un-solve problems that were previously solved, and their solutions create new problems. One must identify and anticipate these new problems.
Remember: If you cannot control it, then measure it in order to forecast or predict it.
Forecasting is a prediction of what will occur in the future, and it is an uncertain process. Because of the uncertainty, the accuracy of a forecast is as important as the outcome predicted by the forecast. This site presents a general overview of business forecasting techniques as classified in the following figure:
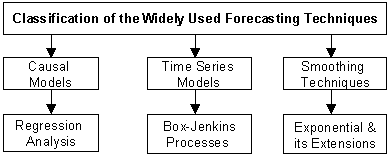
Progressive Approach to Modeling: Modeling for decision making involves two distinct parties, one is the decision-maker and the other is the model-builder known as the analyst. The analyst is to assist the decision-maker in his/her decision-making process. Therefore, the analyst must be equipped with more than a set of analytical methods.
Integrating External Risks and Uncertainties: The mechanisms of thought are often distributed over brain, body and world. At the heart of this view is the fact that where the causal contribution of certain internal elements and the causal contribution of certain external elements are equal in governing behavior, there is no good reason to count the internal elements as proper parts of a cognitive system while denying that status to the external elements.
In improving the decision process, it is critical issue to translating environmental information into the process and action. Climate can no longer be taken for granted:
- Societies are becoming increasingly interdependent.
- The climate system is changing.
- Losses associated with climatic hazards are rising.
The decision process is a platform for both the modeler and the decision maker to engage with human-made climate change. This includes ontological, ethical, and historical aspects of climate change, as well as relevant questions such as:
- Does climate change shed light on the foundational dynamics of reality structures?
- Does it indicate a looming bankruptcy of traditional conceptions of human-nature interplays?
- Does it indicate the need for utilizing nonwestern approaches, and if so, how?
- Does the imperative of sustainable development entail a new groundwork for decision maker?
- How will human-made climate change affect academic modelers -- and how can they contribute positively to the global science and policy of climate change?
Quantitative Decision Making: Schools of Business and Management are flourishing with more and more students taking up degree program at all level. In particular there is a growing market for conversion courses such as MSc in Business or Management and post experience courses such as MBAs. In general, a strong mathematical background is not a pre-requisite for admission to these programs. Perceptions of the content frequently focus on well-understood functional areas such as Marketing, Human Resources, Accounting, Strategy, and Production and Operations. A Quantitative Decision Making, such as this course is an unfamiliar concept and often considered as too hard and too mathematical. There is clearly an important role this course can play in contributing to a well-rounded Business Management degree program specialized, for example in finance.
Specialists in model building are often tempted to study a problem, and then go off in isolation to develop an elaborate mathematical model for use by the manager (i.e., the decision-maker). Unfortunately the manager may not understand this model and may either use it blindly or reject it entirely. The specialist may believe that the manager is too ignorant and unsophisticated to appreciate the model, while the manager may believe that the specialist lives in a dream world of unrealistic assumptions and irrelevant mathematical language.
Such miscommunication can be avoided if the manager works with the specialist to develop first a simple model that provides a crude but understandable analysis. After the manager has built up confidence in this model, additional detail and sophistication can be added, perhaps progressively only a bit at a time. This process requires an investment of time on the part of the manager and sincere interest on the part of the specialist in solving the manager's real problem, rather than in creating and trying to explain sophisticated models. This progressive model building is often referred to as the bootstrapping approach and is the most important factor in determining successful implementation of a decision model. Moreover the bootstrapping approach simplifies the otherwise difficult task of model validation and verification processes.
The time series analysis has three goals: forecasting (also called predicting), modeling, and characterization. What would be the logical order in which to tackle these three goals such that one task leads to and /or and justifies the other tasks? Clearly, it depends on what the prime objective is. Sometimes you wish to model in order to get better forecasts. Then the order is obvious. Sometimes, you just want to understand and explain what is going on. Then modeling is again the key, though out-of-sample forecasting may be used to test any model. Often modeling and forecasting proceed in an iterative way and there is no 'logical order' in the broadest sense. You may model to get forecasts, which enable better control, but iteration is again likely to be present and there are sometimes special approaches to control problems.
Outliers: One cannot nor should not study time series data without being sensitive to outliers. Outliers can be one-time outliers or seasonal pulses or a sequential set of outliers with nearly the same magnitude and direction (level shift) or local time trends. A pulse is a difference of a step while a step is a difference of a time trend. In order to assess or declare "an unusual value" one must develop "the expected or usual value". Time series techniques extended for outlier detection, i.e. intervention variables like pulses, seasonal pulses, level shifts and local time trends can be useful in "data cleansing" or pre-filtering of observations.
Further Readings:
Borovkov K., Elements of Stochastic Modeling, World Scientific Publishing, 2003.
Christoffersen P., Elements of Financial Risk Management, Academic Press, 2003.
Holton G., Value-at-Risk: Theory and Practice, Academic Press, 2003.
Effective Modeling for Good Decision-Making
What is a model? A Model is an external and explicit representation of a part of reality, as it is seen by individuals who wish to use this model to understand, change, manage and control that part of reality."Why are so many models designed and so few used?" is a question often discussed within the Quantitative Modeling (QM) community. The formulation of the question seems simple, but the concepts and theories that must be mobilized to give it an answer are far more sophisticated. Would there be a selection process from "many models designed" to "few models used" and, if so, which particular properties do the "happy few" have? This site first analyzes the various definitions of "models" presented in the QM literature and proposes a synthesis of the functions a model can handle. Then, the concept of "implementation" is defined, and we progressively shift from a traditional "design then implementation" standpoint to a more general theory of a model design/implementation, seen as a cross-construction process between the model and the organization in which it is implemented. Consequently, the organization is considered not as a simple context, but as an active component in the design of models. This leads logically to six models of model implementation: the technocratic model, the political model, the managerial model, the self-learning model, the conquest model and the experimental model.
Succeeding in Implementing a Model: In order that an analyst succeeds in implementing a model that could be both valid and legitimate, here are some guidelines:
- Be ready to work in close co-operation with the strategic stakeholders in order to acquire a sound understanding of the organizational context. In addition, the QM should constantly try to discern the kernel of organizational values from its more contingent part.
- The QM should attempt to strike a balance between the level of model sophistication/complexity and the competence level of stakeholders. The model must be adapted both to the task at hand and to the cognitive capacity of the stakeholders.
- The QM should attempt to become familiar with the various preferences prevailing in the organization. This is important since the interpretation and the use of the model will vary according to the dominant preferences of the various organizational actors.
- The QM should make sure that the possible instrumental uses of the model are well documented and that the strategic stakeholders of the decision making process are quite knowledgeable about and comfortable with the contents and the working of the model.
- The QM should be prepared to modify or develop a new version of the model, or even a completely new model, if needed, that allows an adequate exploration of heretofore unforeseen problem formulation and solution alternatives.
- The QM should make sure that the model developed provides a buffer or leaves room for the stakeholders to adjust and readjust themselves to the situation created by the use of the model and
- The QM should be aware of the pre-conceived ideas and concepts of the stakeholders regarding problem definition and likely solutions; many decisions in this respect might have been taken implicitly long before they become explicit.
In model-based decision-making, we are particularly interested in the idea that a model is designed with a view to action.
Descriptive and prescriptive models: A descriptive model is often a function of figuration, abstraction based on reality. However, a prescriptive model is moving from reality to a model a function of development plan, means of action, moving from model to the reality.
One must distinguishes between descriptive and prescriptive models in the perspective of a traditional analytical distinction between knowledge and action. The prescriptive models are in fact the furthest points in a chain cognitive, predictive, and decision making.
Why modeling? The purpose of models is to aid in designing solutions. They are to assist understanding the problem and to aid deliberation and choice by allowing us to evaluate the consequence of our action before implementing them.
The principle of bounded rationality assumes that the decision maker is able to optimize but only within the limits of his/her representation of the decision problem. Such a requirement is fully compatible with many results in the psychology of memory: an expert uses strategies compiled in the long-term memory and solves a decision problem with the help of his/her short-term working memory.
Problem solving is decision making that may involves heuristics such as satisfaction principle, and availability. It often, involves global evaluations of alternatives that could be supported by the short-term working memory and that should be compatible with various kinds of attractiveness scales. Decision-making might be viewed as the achievement of a more or less complex information process and anchored in the search for a dominance structure: the Decision Maker updates his/her representation of the problem with the goal of finding a case where one alternative dominant all the others for example; in a mathematical approach based on dynamic systems under three principles:
- Parsimony: the decision maker uses a small amount of information.
- Reliability: the processed information is relevant enough to justify -- personally or socially -- decision outcomes.
- Decidability: the processed information may change from one decision to another.
Cognitive science provides us with the insight that a cognitive system, in general, is an association of a physical working device that is environment sensitive through perception and action, with a mind generating mental activities designed as operations, representations, categorizations and/or programs leading to efficient problem-solving strategies.
Mental activities act on the environment, which itself acts again on the system by way of perceptions produced by representations.
Designing and implementing human-centered systems for planning, control, decision and reasoning require studying the operational domains of a cognitive system in three dimensions:
- An environmental dimension, where first, actions performed by a cognitive system may be observed by way of changes in the environment; and second, communication is an observable mode of exchange between different cognitive systems.
- An internal dimension, where mental activities; i.e., memorization and information processing generate changes in the internal states of the system. These activities are, however, influenced by partial factorizations through the environment, such as planning, deciding, and reasoning.
- An autonomous dimension where learning and knowledge acquisition enhance mental activities by leading to the notions of self- reflexivity and consciousness.
Validation and Verification: As part of the calibration process of a model, the modeler must validate and verified the model. The term validation is applied to those processes, which seek to determine whether or not a model is correct with respect to the "real" system. More prosaically, validation is concerned with the question "Are we building the right system?" Verification, on the other hand, seeks to answer the question "Are we building the system right?"
Balancing Success in Business
Without metrics, management can be a nebulous, if not impossible, exercise. How can we tell if we have met our goals if we do not know what our goals are? How do we know if our business strategies are effective if they have not been well defined? For example, one needs a methodology for measuring success and setting goals from financial and operational viewpoints. With those measures, any business can manage its strategic vision and adjust it for any change. Setting a performance measure is a multi-perspective at least from financial, customer, innovation, learning, and internal business viewpoints processes.
- The financial perspective provides a view of how the shareholders see the company; i.e. the company's bottom-line.
- The customer perspective provides a view of how the customers see the company.
- While the financial perspective deals with the projected value of the company, the innovation and learning perspective sets measures that help the company compete in a changing business environment. The focus for this innovation is in the formation of new or the improvement of existing products and processes.
- The internal business process perspective provides a view of what the company must excel at to be competitive. The focus of this perspective then is the translation of customer-based measures into measures reflecting the company's internal operations.
Each of the above four perspectives must be considered with respect to four parameters:
- Goals: What do we need to achieve to become successful?
- Measures: What parameters will we use to know if we are successful?
- Targets: What quantitative value will we use to determine success of the measure?
- Initiatives: What will we do to meet our goals?
Clearly, it is not enough to produce an instrument to document and monitor success. Without proper implementation and leadership, creating a performance measure will remain only an exercise as opposed to a system to manage change.
Further Readings:
Calabro L. On balance, Chief Financial Officer Magazine, February 01, 2001. Almost 10 years after developing the balanced scorecard, authors Robert Kaplan and David Norton share what they've learned.
Craven B., and S. Islam, Optimization in Economics and Finance, Springer , 2005.
Kaplan R., and D. Norton, The balanced scorecard: Measures that drive performance, Harvard Business Review, 71, 1992.
Modeling for Forecasting:
Accuracy and Validation Assessments
Data Gathering for Verification of Model: Data gathering is often considered "expensive". Indeed, technology "softens" the mind, in that we become reliant on devices; however, reliable data are needed to verify a quantitative model. Mathematical models, no matter how elegant, sometimes escape the appreciation of the decision-maker. In other words, some people think algebraically; others see geometrically. When the data are complex or multidimensional, there is the more reason for working with equations, though appealing to the intellect has a more down-to-earth undertone: beauty is in the eye of the other beholder - not you; yourself.
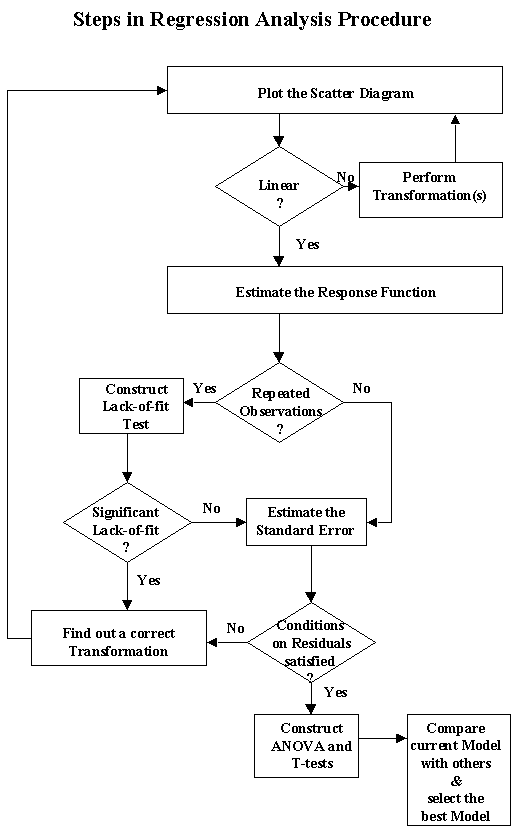
The following flowchart highlights the systematic development of the modeling and forecasting phases:
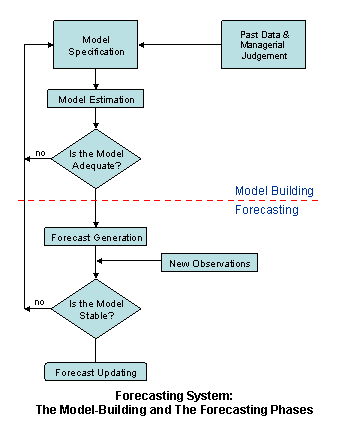
Modeling for Forecasting
Click on the image to enlarge it and THEN print it
The above modeling process is useful to:
- understand the underlying mechanism generating the time series. This includes describing and explaining any variations, seasonallity, trend, etc.
- predict the future under "business as usual" condition.
- control the system, which is to perform the "what-if" scenarios.
Statistical Forecasting: The selection and implementation of the proper forecast methodology has always been an important planning and control issue for most firms and agencies. Often, the financial well-being of the entire operation rely on the accuracy of the forecast since such information will likely be used to make interrelated budgetary and operative decisions in areas of personnel management, purchasing, marketing and advertising, capital financing, etc. For example, any significant over-or-under sales forecast error may cause the firm to be overly burdened with excess inventory carrying costs or else create lost sales revenue through unanticipated item shortages. When demand is fairly stable, e.g., unchanging or else growing or declining at a known constant rate, making an accurate forecast is less difficult. If, on the other hand, the firm has historically experienced an up-and-down sales pattern, then the complexity of the forecasting task is compounded.
There are two main approaches to forecasting. Either the estimate of future value is based on an analysis of factors which are believed to influence future values, i.e., the explanatory method, or else the prediction is based on an inferred study of past general data behavior over time, i.e., the extrapolation method. For example, the belief that the sale of doll clothing will increase from current levels because of a recent advertising blitz rather than proximity to Christmas illustrates the difference between the two philosophies. It is possible that both approaches will lead to the creation of accurate and useful forecasts, but it must be remembered that, even for a modest degree of desired accuracy, the former method is often more difficult to implement and validate than the latter approach.
Autocorrelation: Autocorrelation is the serial correlation of equally spaced time series between its members one or more lags apart. Alternative terms are the lagged correlation, and persistence. Unlike the statistical data which are random samples allowing us to perform statistical analysis, the time series are strongly autocorrelated, making it possible to predict and forecast. Three tools for assessing the autocorrelation of a time series are the time series plot, the lagged scatterplot, and at least the first and second order autocorrelation values.
Standard Error for a Stationary Time-Series: The sample mean for a time-series, has standard error not equal to S / n ½, but S[(1-r) / (n-nr)] ½, where S is the sample standard deviation, n is the length of the time-series, and r is its first order correlation.
Performance Measures and Control Chart for Examine Forecasting Errors: Beside the Standard Error there are other performance measures. The following are some of the widely used performance measures:
Performance Measures for Forecasting
Click on the image to enlarge it and THEN print it
If the forecast error is stable, then the distribution of it is approximately normal. With this in mind, we can plot and then analyze the on the control charts to see if they might be a need to revise the forecasting method being used. To do this, if we divide a normal distribution into zones, with each zone one standard deviation wide, then one obtains the approximate percentage we expect to find in each zone from a stable process.
Modeling for Forecasting with Accuracy and Validation Assessments: Control limits could be one-standard-error, or two-standard-error, and any point beyond these limits (i.e., outside of the error control limit) is an indication the need to revise the forecasting process, as shown below:
A Zone on a Control Chart for Controlling Forecasting Errors
Click on the image to enlarge it and THEN print it
The plotted forecast errors on this chart, not only should remain with the control limits, they should not show any obvious pattern, collectively.
Since validation is used for the purpose of establishing a models credibility it is important that the method used for the validation is, itself, credible. Features of time series, which might be revealed by examining its graph, with the forecasted values, and the residuals behavior, condition forecasting modeling.
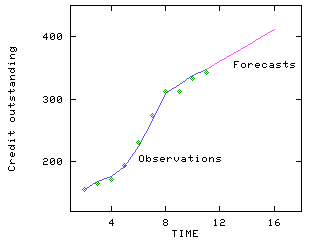
An effective approach to modeling forecasting validation is to hold out a specific number of data points for estimation validation (i.e., estimation period), and a specific number of data points for forecasting accuracy (i.e., validation period). The data, which are not held out, are used to estimate the parameters of the model, the model is then tested on data in the validation period, if the results are satisfactory, and forecasts are then generated beyond the end of the estimation and validation periods. As an illustrative example, the following graph depicts the above process on a set of data with trend component only:

Estimation Period, Validation Period, and the Forecasts
Click on the image to enlarge it and THEN print it
In general, the data in the estimation period are used to help select the model and to estimate its parameters. Forecasts into the future are "real" forecasts that are made for time periods beyond the end of the available data.
The data in the validation period are held out during parameter estimation. One might also withhold these values during the forecasting analysis after model selection, and then one-step-ahead forecasts are made.
A good model should have small error measures in both the estimation and validation periods, compared to other models, and its validation period statistics should be similar to its own estimation period statistics.
Holding data out for validation purposes is probably the single most important diagnostic test of a model: it gives the best indication of the accuracy that can be expected when forecasting the future. It is a rule-of-thumb that one should hold out at least 20% of data for validation purposes.
You may like using the Time Series' Statistics JavaScript for computing some of the essential statistics needed for a preliminary investigation of your time series.
Stationary Time Series
Stationarity has always played a major role in time series analysis. To perform forecasting, most techniques required stationarity conditions. Therefore, we need to establish some conditions, e.g. time series must be a first and second order stationary process.First Order Stationary: A time series is a first order stationary if expected value of X(t) remains the same for all t.
For example in economic time series, a process is first order stationary when we remove any kinds of trend by some mechanisms such as differencing.
Second Order Stationary: A time series is a second order stationary if it is first order stationary and covariance between X(t) and X(s) is function of length (t-s) only.
Again, in economic time series, a process is second order stationary when we stabilize also its variance by some kind of transformations, such as taking square root.
You may like using Test for Stationary Time Series JavaScript.
Statistics for Correlated Data
We concern ourselves with n realizations that are related to time, that is having n correlated observations; the estimate of the mean is given by
Let
where the sum is over j = 1 to m, then the estimated variance is:
Where
As a good rule of thumb, the maximum lag for which autocorrelations are computed should be approximately 2% of the number of n realizations, although each rj,x could be tested to determine if it is significantly different from zero.
Sample Size Determination: We can calculate the minimum sample size required by
Application: A pilot run was made of a model, observations numbered 150, the mean was 205.74 minutes and the variance S2 = 101, 921.54, estimate of the lag coefficients were computed as: r1,x = 0.3301 r2,x = 0.2993, and r3,x = 0.1987. Calculate the minimum sample size to assure the estimate lies within +d = 10% of the true mean with a = 0.05.
You may like using Statistics for Time Series, and Testing Correlation JavaScript.
A Summary of Forecasting Methods
Ideally, organizations which can afford to do so will usually assign crucial forecast responsibilities to those departments and/or individuals that are best qualified and have the necessary resources at hand to make such forecast estimations under complicated demand patterns. Clearly, a firm with a large ongoing operation and a technical staff comprised of statisticians, management scientists, computer analysts, etc. is in a much better position to select and make proper use of sophisticated forecast techniques than is a company with more limited resources. Notably, the bigger firm, through its larger resources, has a competitive edge over an unwary smaller firm and can be expected to be very diligent and detailed in estimating forecast (although between the two, it is usually the smaller firm which can least afford miscalculations in new forecast levels).
A time series is a set of ordered observations on a quantitative characteristic of a phenomenon at equally spaced time points. One of the main goals of time series analysis is to forecast future values of the series.
A trend is a regular, slowly evolving change in the series level. Changes that can be modeled by low-order polynomials
We examine three general classes of models that can be constructed for purposes of forecasting or policy analysis. Each involves a different degree of model complexity and presumes a different level of comprehension about the processes one is trying to model.
Many of us often either use or produce forecasts of one sort or another. Few of us recognize, however, that some kind of logical structure, or model, is implicit in every forecast.
In making a forecast, it is also important to provide a measure of how accurate one can expect the forecast to be. The use of intuitive methods usually precludes any quantitative measure of confidence in the resulting forecast. The statistical analysis of the individual relationships that make up a model, and of the model as a whole, makes it possible to attach a measure of confidence to the models forecasts.
Once a model has been constructed and fitted to data, a sensitivity analysis can be used to study many of its properties. In particular, the effects of small changes in individual variables in the model can be evaluated. For example, in the case of a model that describes and predicts interest rates, one could measure the effect on a particular interest rate of a change in the rate of inflation. This type of sensitivity study can be performed only if the model is an explicit one.
In Time-Series Models we presume to know nothing about the causality that affects the variable we are trying to forecast. Instead, we examine the past behavior of a time series in order to infer something about its future behavior. The method used to produce a forecast may involve the use of a simple deterministic model such as a linear extrapolation or the use of a complex stochastic model for adaptive forecasting.
One example of the use of time-series analysis would be the simple extrapolation of a past trend in predicting population growth. Another example would be the development of a complex linear stochastic model for passenger loads on an airline. Time-series models have been used to forecast the demand for airline capacity, seasonal telephone demand, the movement of short-term interest rates, and other economic variables. Time-series models are particularly useful when little is known about the underlying process one is trying to forecast. The limited structure in time-series models makes them reliable only in the short run, but they are nonetheless rather useful.
In the Single-Equation Regression Models the variable under study is explained by a single function (linear or nonlinear) of a number of explanatory variables. The equation will often be time-dependent (i.e., the time index will appear explicitly in the model), so that one can predict the response over time of the variable under study to changes in one or more of the explanatory variables. A principal purpose for constructing single-equation regression models is forecasting. A forecast is a quantitative estimate (or set of estimates) about the likelihood of future events which is developed on the basis of past and current information. This information is embodied in the form of a modela single-equation structural model and a multi-equation model or a time-series model. By extrapolating our models beyond the period over which they were estimated, we can make forecasts about near future events. This section shows how the single-equation regression model can be used as a forecasting tool.
The term forecasting is often thought to apply solely to problems in which we predict the future. We shall remain consistent with this notion by orienting our notation and discussion toward time-series forecasting. We stress, however, that most of the analysis applies equally well to cross-section models.
An example of a single-equation regression model would be an equation that relates a particular interest rate, such as the money supply, the rate of inflation, and the rate of change in the gross national product.
The choice of the type of model to develop involves trade-offs between time, energy, costs, and desired forecast precision. The construction of a multi-equation simulation model may require large expenditures of time and money. The gains from this effort may include a better understanding of the relationships and structure involved as well as the ability to make a better forecast. However, in some cases these gains may be small enough to be outweighed by the heavy costs involved. Because the multi-equation model necessitates a good deal of knowledge about the process being studied, the construction of such models may be extremely difficult.
The decision to build a time-series model usually occurs when little or nothing is known about the determinants of the variable being studied, when a large number of data points are available, and when the model is to be used largely for short-term forecasting. Given some information about the processes involved, however, it may be reasonable for a forecaster to construct both types of models and compare their relative performance.
Two types of forecasts can be useful. Point forecasts predict a single number in each forecast period, while interval forecasts indicate an interval in which we hope the realized value will lie. We begin by discussing point forecasts, after which we consider how confidence intervals (interval forecasts) can be used to provide a margin of error around point forecasts.
The information provided by the forecasting process can be used in many ways. An important concern in forecasting is the problem of evaluating the nature of the forecast error by using the appropriate statistical tests. We define the best forecast as the one which yields the forecast error with the minimum variance. In the single-equation regression model, ordinary lest-squares estimation yields the best forecast among all linear unbiased estimators having minimum mean-square error.
The error associated with a forecasting procedure can come from a combination of four distinct sources. First, the random nature of the additive error process in a linear regression model guarantees that forecasts will deviate from true values even if the model is specified correctly and its parameter values are known. Second, the process of estimating the regression parameters introduces error because estimated parameter values are random variables that may deviate from the true parameter values. Third, in the case of a conditional forecast, errors are introduced when forecasts are made for the values of the explanatory variables for the period in which the forecast is made. Fourth, errors may be introduced because the model specification may not be an accurate representation of the "true" model.
Multi-predictor regression methods include logistic models for binary outcomes, the Cox model for right-censored survival times, repeated-measures models for longitudinal and hierarchical outcomes, and generalized linear models for counts and other outcomes. Below we outline some effective forecasting approaches, especially for short to intermediate term analysis and forecasting:
Modeling the Causal Time Series: With multiple regressions, we can use more than one predictor. It is always best, however, to be parsimonious, that is to use as few variables as predictors as necessary to get a reasonably accurate forecast. Multiple regressions are best modeled with commercial package such as SAS or SPSS. The forecast takes the form:
where b0 is the intercept, b1, b2, . . . bn are coefficients representing the contribution of the independent variables X1, X2,..., Xn.
Forecasting is a prediction of what will occur in the future, and it is an uncertain process. Because of the uncertainty, the accuracy of a forecast is as important as the outcome predicted by forecasting the independent variables X1, X2,..., Xn. A forecast control must be used to determine if the accuracy of the forecast is within acceptable limits. Two widely used methods of forecast control are a tracking signal, and statistical control limits.
Tracking signal is computed by dividing the total residuals by their mean absolute deviation (MAD). To stay within 3 standard deviations, the tracking signal that is within 3.75 MAD is often considered to be good enough.
Statistical control limits are calculated in a manner similar to other quality control limit charts, however, the residual standard deviation are used.
Multiple regressions are used when two or more independent factors are involved, and it is widely used for short to intermediate term forecasting. They are used to assess which factors to include and which to exclude. They can be used to develop alternate models with different factors.
Trend Analysis: Uses linear and nonlinear regression with time as the explanatory variable, it is used where pattern over time have a long-term trend. Unlike most time-series forecasting techniques, the Trend Analysis does not assume the condition of equally spaced time series.
Nonlinear regression does not assume a linear relationship between variables. It is frequently used when time is the independent variable.
You may like using Detective Testing for Trend JavaScript.
In the absence of any "visible" trend, you may like performing the Test for Randomness of Fluctuations, too.
Modeling Seasonality and Trend: Seasonality is a pattern that repeats for each period. For example annual seasonal pattern has a cycle that is 12 periods long, if the periods are months, or 4 periods long if the periods are quarters. We need to get an estimate of the seasonal index for each month, or other periods, such as quarter, week, etc, depending on the data availability.
1. Seasonal Index: Seasonal index represents the extent of seasonal influence for a particular segment of the year. The calculation involves a comparison of the expected values of that period to the grand mean.
A seasonal index is how much the average for that particular period tends to be above (or below) the grand average. Therefore, to get an accurate estimate for the seasonal index, we compute the average of the first period of the cycle, and the second period, etc, and divide each by the overall average. The formula for computing seasonal factors is:
Si = the seasonal index for ith period,
Di = the average values of ith period,
D = grand average,
i = the ith seasonal period of the cycle.
A seasonal index of 1.00 for a particular month indicates that the expected value of that month is 1/12 of the overall average. A seasonal index of 1.25 indicates that the expected value for that month is 25% greater than 1/12 of the overall average. A seasonal index of 80 indicates that the expected value for that month is 20% less than 1/12 of the overall average.
2. Deseasonalizing Process: Deseasonalizing the data, also called Seasonal Adjustment is the process of removing recurrent and periodic variations over a short time frame, e.g., weeks, quarters, months. Therefore, seasonal variations are regularly repeating movements in series values that can be tied to recurring events. The Deseasonalized data is obtained by simply dividing each time series observation by the corresponding seasonal index.
Almost all time series published by the US government are already deseasonalized using the seasonal index to unmasking the underlying trends in the data, which could have been caused by the seasonality factor.
3. Forecasting: Incorporating seasonality in a forecast is useful when the time series has both trend and seasonal components. The final step in the forecast is to use the seasonal index to adjust the trend projection. One simple way to forecast using a seasonal adjustment is to use a seasonal factor in combination with an appropriate underlying trend of total value of cycles.
4. A Numerical Application: The following table provides monthly sales ($1000) at a college bookstore. The sales show a seasonal pattern, with the greatest number when the college is in session and decrease during the summer months.
|
Suppose we wish to calculate seasonal factors and a trend, then calculate the forecasted sales for July in year 5.
The first step in the seasonal forecast will be to compute monthly indices using the past four-year sales. For example, for January the index is:
Similar calculations are made for all other months. Indices are summarized in the last row of the above table. Notice that the mean (average value) for the monthly indices adds up to 12, which is the number of periods in a year for the monthly data.
Next, a linear trend often is calculated using the annual sales:
|
||||||||||||||||||||||||
Often fitting a straight line to the seasonal data is misleading. By constructing the scatter-diagram, we notice that a Parabola might be a better fit. Using the Polynomial Regression JavaScript, the estimated quadratic trend is:
Predicted values using both the linear and the quadratic trends are presented in the above tables. Comparing the predicted values of the two models with the actual data indicates that the quadratic trend is a much superior fit than the linear one, as often expected.
We can now forecast the next annual sales; which, corresponds to year 5, or T = 5 in the above quadratic equation:
Finally, the forecast for month of July is calculated by multiplying the average monthly sales forecast by the July seasonal index, which is 0.79; i.e., (264.25).(0.79) or 209.
You might like to use the Seasonal Index JavaScript to check your hand computation. As always you must first use Plot of the Time Series as a tool for the initial characterization process.
For testing seasonality based on seasonal index, you may like to use the Test for Seasonality JavaScript.
Trend Removal and Cyclical Analysis: The cycles can be easily studied if the trend itself is removed. This is done by expressing each actual value in the time series as a percentage of the calculated trend for the same date. The resulting time series has no trend, but oscillates around a central value of 100.
Decomposition Analysis: It is the pattern generated by the time series and not necessarily the individual data values that offers to the manager who is an observer, a planner, or a controller of the system. Therefore, the Decomposition Analysis is used to identify several patterns that appear simultaneously in a time series.
A variety of factors are likely influencing data. It is very important in the study that these different influences or components be separated or decomposed out of the 'raw' data levels. In general, there are four types of components in time series analysis: Seasonality, Trend, Cycling and Irregularity.
The first three components are deterministic which are called "Signals", while the last component is a random variable, which is called "Noise". To be able to make a proper forecast, we must know to what extent each component is present in the data. Hence, to understand and measure these components, the forecast procedure involves initially removing the component effects from the data (decomposition). After the effects are measured, making a forecast involves putting back the components on forecast estimates (recomposition). The time series decomposition process is depicted by the following flowchart:

Definitions of the major components in the above flowchart:Seasonal variation: When a repetitive pattern is observed over some time horizon, the series is said to have seasonal behavior. Seasonal effects are usually associated with calendar or climatic changes. Seasonal variation is frequently tied to yearly cycles.
Trend: A time series may be stationary or exhibit trend over time. Long-term trend is typically modeled as a linear, quadratic or exponential function.
Cyclical variation: An upturn or downturn not tied to seasonal variation. Usually results from changes in economic conditions.
- Seasonalities are regular fluctuations which are repeated from year to year with about the same timing and level of intensity. The first step of a times series decomposition is to remove seasonal effects in the data. Without deseasonalizing the data, we may, for example, incorrectly infer that recent increase patterns will continue indefinitely; i.e., a growth trend is present, when actually the increase is 'just because it is that time of the year'; i.e., due to regular seasonal peaks. To measure seasonal effects, we calculate a series of seasonal indexes. A practical and widely used method to compute these indexes is the ratio-to-moving-average approach. From such indexes, we may quantitatively measure how far above or below a given period stands in comparison to the expected or 'business as usual' data period (the expected data are represented by a seasonal index of 100%, or 1.0).
- Trend is growth or decay that is the tendencies for data to increase or decrease fairly steadily over time. Using the deseasonalized data, we now wish to consider the growth trend as noted in our initial inspection of the time series. Measurement of the trend component is done by fitting a line or any other function. This fitted function is calculated by the method of least squares and represents the overall trend of the data over time.
- Cyclic oscillations are general up-and-down data changes; due to changes e.g., in the overall economic environment (not caused by seasonal effects) such as recession-and-expansion. To measure how the general cycle affects data levels, we calculate a series of cyclic indexes. Theoretically, the deseasonalized data still contains trend, cyclic, and irregular components. Also, we believe predicted data levels using the trend equation do represent pure trend effects. Thus, it stands to reason that the ratio of these respective data values should provide an index which reflects cyclic and irregular components only. As the business cycle is usually longer than the seasonal cycle, it should be understood that cyclic analysis is not expected to be as accurate as a seasonal analysis.
Due to the tremendous complexity of general economic factors on long term behavior, a general approximation of the cyclic factor is the more realistic aim. Thus, the specific sharp upturns and downturns are not so much the primary interest as the general tendency of the cyclic effect to gradually move in either direction. To study the general cyclic movement rather than precise cyclic changes (which may falsely indicate more accurately than is present under this situation), we 'smooth' out the cyclic plot by replacing each index calculation often with a centered 3-period moving average. The reader should note that as the number of periods in the moving average increases, the smoother or flatter the data become. The choice of 3 periods perhaps viewed as slightly subjective may be justified as an attempt to smooth out the many up-and-down minor actions of the cycle index plot so that only the major changes remain.
- Irregularities (I) are any fluctuations not classified as one of the above. This component of the time series is unexplainable; therefore it is unpredictable. Estimation of I can be expected only when its variance is not too large. Otherwise, it is not possible to decompose the series. If the magnitude of variation is large, the projection for the future values will be inaccurate. The best one can do is to give a probabilistic interval for the future value given the probability of I is known.
- Making a Forecast: At this point of the analysis, after we have completed the study of the time series components, we now project the future values in making forecasts for the next few periods. The procedure is summarized below.
- Step 1: Compute the future trend level using the trend equation.
- Step 2: Multiply the trend level from Step 1 by the period seasonal index to include seasonal effects.
- Step 3: Multiply the result of Step 2 by the projected cyclic index to include cyclic effects and get the final forecast result.
Exercise your knowledge about how to forecast by decomposition method? by using a sales time series available at
Therein you will find a detailed workout numerical example in the context of the sales time series which consists of all components including a cycle.
Smoothing Techniques: A time series is a sequence of observations, which are ordered in time. Inherent in the collection of data taken over time is some form of random variation. There exist methods for reducing of canceling the effect due to random variation. A widely used technique is "smoothing". This technique, when properly applied, reveals more clearly the underlying trend, seasonal and cyclic components.
Smoothing techniques are used to reduce irregularities (random fluctuations) in time series data. They provide a clearer view of the true underlying behavior of the series. Moving averages rank among the most popular techniques for the preprocessing of time series. They are used to filter random "white noise" from the data, to make the time series smoother or even to emphasize certain informational components contained in the time series.
Exponential smoothing is a very popular scheme to produce a smoothed time series. Whereas in moving averages the past observations are weighted equally, Exponential Smoothing assigns exponentially decreasing weights as the observation get older. In other words, recent observations are given relatively more weight in forecasting than the older observations. Double exponential smoothing is better at handling trends. Triple Exponential Smoothing is better at handling parabola trends.
Exponential smoothing is a widely method used of forecasting based on the time series itself. Unlike regression models, exponential smoothing does not imposed any deterministic model to fit the series other than what is inherent in the time series itself.
Simple Moving Averages: The best-known forecasting methods is the moving averages or simply takes a certain number of past periods and add them together; then divide by the number of periods. Simple Moving Averages (MA) is effective and efficient approach provided the time series is stationary in both mean and variance. The following formula is used in finding the moving average of order n, MA(n) for a period t+1,
where n is the number of observations used in the calculation.
The forecast for time period t + 1 is the forecast for all future time periods. However, this forecast is revised only when new data becomes available.
You may like using Forecasting by Smoothing Javasript, and then performing some numerical experimentation for a deeper understanding of these concepts.
Weighted Moving Average: Very powerful and economical. They are widely used where repeated forecasts required-uses methods like sum-of-the-digits and trend adjustment methods. As an example, a Weighted Moving Averages is:
where the weights are any positive numbers such that: w1 + w2 + w3 = 1. A typical weights for this example is, w1 = 3/(1 + 2 + 3) = 3/6, w2 = 2/6, and w3 = 1/6.
You may like using Forecasting by Smoothing JavaScript, and then performing some numerical experimentation for a deeper understanding of the concepts.
An illustrative numerical example: The moving average and weighted moving average of order five are calculated in the following table.
| Week | Sales ($1000) | MA(5) | WMA(5) |
|---|---|---|---|
| 1 | 105 | - | - |
| 2 | 100 | - | - |
| 3 | 105 | - | - |
| 4 | 95 | - | - |
| 5 | 100 | 101 | 100 |
| 6 | 95 | 99 | 98 |
| 7 | 105 | 100 | 100 |
| 8 | 120 | 103 | 107 |
| 9 | 115 | 107 | 111 |
| 10 | 125 | 117 | 116 |
| 11 | 120 | 120 | 119 |
| 12 | 120 | 120 | 119 |
Moving Averages with Trends: Any method of time series analysis involves a different degree of model complexity and presumes a different level of comprehension about the underlying trend of the time series. In many business time series, the trend in the smoothed series using the usual moving average method indicates evolving changes in the series level to be highly nonlinear.
In order to capture the trend, we may use the Moving-Average with Trend (MAT) method. The MAT method uses an adaptive linearization of the trend by means of incorporating a combination of the local slopes of both the original and the smoothed time series.
The following formulas are used in MAT method:
X(t): The actual (historical) data at time t.
M(t) = å X(i) / n
i.e., finding the moving average smoothing M(t) of order n, which is a positive odd integer number ³ 3, for i from t-n+1 to t.
F(t) = the smoothed series adjusted for any local trend
F(t) = F(t-1) + a [(n-1)X(t) + (n+1)X(t-n) -2nM(t-1)], where constant coefficient a = 6/(n3 n).
with initial conditions F(t) =X(t) for all t £ n,
Finally, the h-step-a-head forecast f(t+h) is:
F(t+h) = M(t) + [h + (n-1)/2] F(t).
To have a notion of F(t), notice that the inside bracket can be written as:
n[X(t) F(t-1)] + n[X(t-m) F(t-1)] + [X(t-m) X(t)],
this is, a combination of three rise/fall terms.
In making a forecast, it is also important to provide a measure of how accurate one can expect the forecast to be. The statistical analysis of the error terms known as residual time-series provides measure tool and decision process for modeling selection process. In applying MAT method sensitivity analysis is needed to determine the optimal value of the moving average parameter n, i.e., the optimal number of period m. The error time series allows us to study many of its statistical properties for goodness-of-fit decision. Therefore it is important to evaluate the nature of the forecast error by using the appropriate statistical tests. The forecast error must be a random variable distributed normally with mean close to zero and a constant variance across time.
For computer implementation of the Moving Average with Trend (MAT) method one may use the forecasting (FC) module of WinQSB which is commercial grade stand-alone software. WinQSBs approach is to first select the model and then enter the parameters and the data. With the Help features in WinQSB there is no learning-curve one just needs a few minutes to master its useful features.
Exponential Smoothing Techniques: One of the most successful forecasting methods is the exponential smoothing (ES) techniques. Moreover, it can be modified efficiently to use effectively for time series with seasonal patterns. It is also easy to adjust for past errors-easy to prepare follow-on forecasts, ideal for situations where many forecasts must be prepared, several different forms are used depending on presence of trend or cyclical variations. In short, an ES is an averaging technique that uses unequal weights; however, the weights applied to past observations decline in an exponential manner.
Single Exponential Smoothing: It calculates the smoothed series as a damping coefficient times the actual series plus 1 minus the damping coefficient times the lagged value of the smoothed series. The extrapolated smoothed series is a constant, equal to the last value of the smoothed series during the period when actual data on the underlying series are available. While the simple Moving Average method is a special case of the ES, the ES is more parsimonious in its data usage.
where:
-
Dt is the actual value
- Ft is the forecasted value
- a is the weighting factor, which ranges from 0 to 1
- t is the current time period.
Notice that the smoothed value becomes the forecast for period t + 1.
A small a provides a detectable and visible smoothing. While a large a provides a fast response to the recent changes in the time series but provides a smaller amount of smoothing. Notice that the exponential smoothing and simple moving average techniques will generate forecasts having the same average age of information if moving average of order n is the integer part of (2-a)/a.
An exponential smoothing over an already smoothed time series is called double-exponential smoothing. In some cases, it might be necessary to extend it even to a triple-exponential smoothing. While simple exponential smoothing requires stationary condition, the double-exponential smoothing can capture linear trends, and triple-exponential smoothing can handle almost all other business time series.
Double Exponential Smoothing: It applies the process described above three to account for linear trend. The extrapolated series has a constant growth rate, equal to the growth of the smoothed series at the end of the data period.
Triple Double Exponential Smoothing: It applies the process described above three to account for nonlinear trend.
Exponenentially Weighted Moving Average: Suppose each day's forecast value is based on the previous day's value so that the weight of each observation drops exponentially the further back (k) in time it is. The weight of any individual is
This approximation is helpful, however, it is harder to update, and may not correspond to an optimal forecast.
Smoothing techniques, such as the Moving Average, Weighted Moving Average, and Exponential Smoothing, are well suited for one-period-ahead forecasting as implemented in the following JavaScript: Forecasting by Smoothing.
Holt's Linear Exponential Smoothing Technique: Suppose that the series { yt } is non-seasonal but does display trend. Now we need to estimate both the current level and the current trend. Here we define the trend Tt at time t as the difference between the current and previous level.
The updating equations express ideas similar to those for exponential smoothing. The equations are:
Given that the level and trend remain unchanged, the initial (starting) values are
Applying the Holts techniques with smoothing with parameters a = 0.7 and b = 0.6, a graphical representation of the time series, its forecasts, together wit a few-step ahead forecasts, are depicted below:
|
|
|||||||||||||||||||||||||||||||||||||||||||
Demonstration of the calculation procedure, with a = 0.7 and b = 0.6
L2 = y2 = 155, T2 = y2 - y1 = 155 133 = 22
L3 = .7 y3 + (1 - .7) F3, T3 = .6 ( L3 - L2 ) + (1 - .6) T2
F4 = L3 + T3, F3 = L2 + T2
L3 = .7 y3 + (1 - .7) F3, T3 = .6 ( L3 - L2 ) + (1 - .6) T2 , F4 = L3 + T3
The Holt-Winters' Forecasting Technique: Now in addition to Holt parameters, suppose that the series exhibits multiplicative seasonality and let St be the multiplicative seasonal factor at time t. Suppose also that there are s periods in a year, so s=4 for quarterly data and s=12 for monthly data. St-s is the seasonal factor in the same period last year.
In some time series, seasonal variation is so strong it obscures any trends or cycles, which are very important for the understanding of the process being observed. Winters smoothing method can remove seasonality and makes long term fluctuations in the series stand out more clearly. A simple way of detecting trend in seasonal data is to take averages over a certain period. If these averages change with time we can say that there is evidence of a trend in the series. The updating equations are:
Tt = b ( Lt - Lt-1 ) + (1 - b) Tt-1
for the trend, and
for the seasonal factor.
We now have three smoothing parameters a , b, and g all must be positive and less than one.
To obtain starting values, one may use the first a few year data. For example for quarterly data, to estimate the level, one may use a centered 4-point moving average:
as the trend estimate for period 10.
as the seasonal factor in period 7. Similarly,
S8 = (y8 / L8 + y4 / L4 ) / 2, S9 = (y9 / L9 + y5 / L5 ) / 2, S10 = (y10 / L10 + y6 / L6 ) / 2
For Monthly Data, the correspondingly we use a centered 12-point moving average:
as the level estimate in period 30.
as the trend estimate for period 30.
Forecasting by the Z-Chart
Another method of short-term forecasting is the use of a Z-Chart. The name Z-Chart arises from the fact that the pattern on such a graph forms a rough letter Z. For example, in a situation where the sales volume figures for one product or product group for the first nine months of a particular year are available, it is possible, using the Z-Chart, to predict the total sales for the year, i.e. to make a forecast for the next three months. It is assumed that basic trading conditions do not alter, or alter on anticipated course and that any underlying trends at present being experienced will continue. In addition to the monthly sales totals for the nine months of the current year, the monthly sales figures for the previous year are also required and are shown in following table:
Year |
||
Month |
2003 $ |
2004 $ |
January |
940 |
520 |
February |
580 |
380 |
March |
690 |
480 |
April |
680 |
490 |
May |
710 |
370 |
June |
660 |
390 |
July |
630 |
350 |
August |
470 |
440 |
September |
480 |
360 |
October |
590 |
|
November |
450 |
|
December |
430 |
|
Total Sales 2003 |
7310 |
|
The monthly sales for the first nine months of a particular year together with the monthly sales for the previous year.
From the data in the above table, another table can be derived and is shown as follows:
The first column in Table 18 relates to actual sales; the seconds to the cumulative total which is found by adding each months sales to the total of preceding sales. Thus, January 520 plus February 380 produces the February cumulative total of 900; the March cumulative total is found by adding the March sales of 480 to the previous cumulative total of 900 and is, therefore, 1,380.
The 12 months moving total is found by adding the sales in the current to the total of the previous 12 months and then subtracting the corresponding month for last year.
Month 2004 |
Actual Sales $ |
Cumulative Total $ |
12 months moving total $ |
January |
520 |
520 |
6890 |
February |
380 |
900 |
6690 |
March |
480 |
1380 |
6480 |
April |
490 |
1870 |
6290 |
May |
370 |
2240 |
5950 |
June |
390 |
2630 |
5680 |
July |
350 |
2980 |
5400 |
August |
440 |
3420 |
5370 |
September |
360 |
3780 |
5250 |
Showing processed monthly sales data, producing a cumulative total and a 12 months moving total.
For example, the 12 months moving total for 2003 is 7,310 (see the above first table). Add to this the January 2004 item 520 which totals 7,830 subtract the corresponding month last year, i.e. the January 2003 item of 940 and the result is the January 2004, 12 months moving total, 6,890.
The 12 months moving total is particularly useful device in forecasting because it includes all the seasonal fluctuations in the last 12 months period irrespective of the month from which it is calculated. The year could start in June and end the next July and contain all the seasonal patterns.
The two groups of data, cumulative totals and the 12 month moving totals shown in the above table are then plotted (A and B), along a line that continues their present trend to the end of the year where they meet:

Forecasting by the Z-Chart
Click on the image to enlarge it
In the above figure, A and B represent the 12 months moving total,and the cumulative data, respectively, while their projections into future are shown by the doted lines.
Notice that, the 12 months accumulation of sales figures is bound to meet the 12 months moving total as they represent different ways of obtaining the same total. In the above figure these lines meet at $4,800, indicating the total sales for the year and forming a simple and approximate method of short-term forecasting.
The above illustrative monthly numerical example approach might be adapted carefully to your set of time series data with any equally spaced intervals.
As an alternative to graphical method, one may fit a linear regression based on the data of lines A and/or B available from the above table, and then extrapolate to obtain short-term forecasting with a desirable confidence level.
Concluding Remarks: A time series is a sequence of observations which are ordered in time. Inherent in the collection of data taken over time is some form of random variation. There exist methods for reducing of canceling the effect due to random variation. Widely used techniques are "smoothing". These techniques, when properly applied, reveals more clearly the underlying trends. In other words, smoothing techniques are used to reduce irregularities (random fluctuations) in time series data. They provide a clearer view of the true underlying behavior of the series.
Exponential smoothing has proven through the years to be very useful in many forecasting situations. Holt first suggested it for non-seasonal time series with or without trends. Winters generalized the method to include seasonality, hence the name: Holt-Winters Method. Holt-Winters method has 3 updating equations, each with a constant that ranges from (0 to 1). The equations are intended to give more weight to recent observations and less weight to observations further in the past. This form of exponential smoothing can be used for less-than-annual periods (e.g., for monthly series). It uses smoothing parameters to estimate the level, trend, and seasonality. Moreover, there are two different procedures, depending on whether seasonality is modeled in an additive or multiplicative way. We will present its multiplicative version; the additive can be applied on an ant-logarithmic function of the data.
The single exponential smoothing emphasizes the short-range perspective; it sets the level to the last observation and is based on the condition that there is no trend. The linear regression, which fits a least squares line to the historical data (or transformed historical data), represents the long range, which is conditioned on the basic trend. Holts linear exponential smoothing captures information about recent trend. The parameters in Holts model are the levels-parameter which should be decreased when the amount of data variation is large, and trends-parameter should be increased if the recent trend direction is supported by the causal some factors.
Since finding three optimal, or even near optimal, parameters for updating equations is not an easy task, an alternative approach to Holt-Winters methods is to deseasonalize the data and then use exponential smoothing. Moreover, in some time series, seasonal variation is so strong it obscures any trends or cycles, which are very important for the understanding of the process being observed. Smoothing can remove seasonality and makes long term fluctuations in the series stand out more clearly. A simple way of detecting trend in seasonal data is to take averages over a certain period. If these averages change with time we can say that there is evidence of a trend in the series.
How to compare several smoothing methods: Although there are numerical indicators for assessing the accuracy of the forecasting technique, the most widely approach is in using visual comparison of several forecasts to assess their accuracy and choose among the various forecasting methods. In this approach, one must plot (using, e.g., Excel) on the same graph the original values of a time series variable and the predicted values from several different forecasting methods, thus facilitating a visual comparison.
You may like using Forecasting by Smoothing Techniques JavaScript.
Further Reading:
Yar, M and C. Chatfield (1990), Prediction intervals for the Holt-Winters forecasting procedure, International Journal of Forecasting 6, 127-137.
Filtering Techniques: Often on must filters an entire, e.g., financial time series with certain filter specifications to extract useful information by a transfer function expression. The aim of a filter function is to filter a time series in order to extract useful information hidden in the data, such as cyclic component. The filter is a direct implementation of and input-output function.
Data filtering is widely used as an effective and efficient time series modeling tool by applying an appropriate transformation technique. Most time series analysis techniques involve some form of filtering out noise in order to make the pattern more salient.
Differencing: A special type of filtering which is particularly useful for removing a trend, is simply to difference a given time series until it becomes stationary. This method is useful in Box-Jenkins modeling. For non-seasonal data, first order differencing is usually sufficient to attain apparent stationarity, so that the new series is formed from the original series.
Adaptive Filtering Any smoothing techniques such as moving average which includes a method of learning from past errors can respond to changes in the relative importance of trend, seasonal, and random factors. In the adaptive exponential smoothing method, one may adjust a to allow for shifting patterns.
Hodrick-Prescott Filter: The Hodrick-Prescott filter or H-P filter is an algorithm for choosing smoothed values for a time series. The H-P filter chooses smooth values {st} for the series {xt} of T elements (t = 1 to T) that solve the following minimization problem:
For the study of business cycles one uses not the smoothed series, but the jagged series of residuals from it. H-P filtered data shows less fluctuation than first-differenced data, since the H-P filter pays less attention to high frequency movements. H-P filtered data also shows more serial correlation than first-differenced data.
This is a smoothing mechanism used to obtain a long term trend component in a time series. It is a way to decompose a given series into stationary and non-stationary components in such a way that their sum of squares of the series from the non-stationary component is minimum with a penalty on changes to the derivatives of the non-stationary component.
Kalman Filter: The Kalman filter is an algorithm for sequentially updating a linear projection for a dynamic system that is in state-space representation. Application of the Kalman filter transforms a system of the following two-equation kind into a more solvable form:
x t+1=Axt+Cw t+1, and yt=Gxt+vt in which: A, C, and G are matrices known as functions of a parameter q about which inference is desired where: t is a whole number, usually indexing time; xt is a true state variable, hidden from the econometrician; yt is a measurement of x with scaling factor G, and measurement errors vt, wt are innovations to the hidden xt process, E(wt+1wt')=1 by normalization (where, ' means the transpose), E(vtvt)=R, an unknown matrix, estimation of which is necessary but ancillary to the problem of interest, which is to get an estimate of q. The Kalman filter defines two matrices St and Kt such that the system described above can be transformed into the one below, in which estimation and inference about q and R is more straightforward; e.g., by regression analysis:
zt+1=Azt+Kat, and yt=Gzt+at where zt is defined to be Et-1xt, at is defined to be yt-E(yt-1yt, K is defined to be limit Kt as t approaches infinity.
The definition of those two matrices St and Kt is itself most of the definition of the Kalman filters: Kt=AStG'(GStG'+R)-1, and St-1=(A-KtG)St (A-KtG)'+CC'+Kt RKt' , Kt is often called the Kalman gain.
Further Readings:
Hamilton J, Time Series Analysis, Princeton University Press, 1994.
Harvey A., Forecasting, Structural Time Series Models and the Kalman Filter, Cambridge University Press, 1991.
Cardamone E., From Kalman to Hodrick-Prescott Filter, 2006.
Mills T., The Econometric Modelling of Financial Time Series, Cambridge University Press, 1995.
Neural Network: For time series forecasting, the prediction model of order p, has the general form:
Neural network architectures can be trained to predict the future values of the dependent variables. What is required are design of the network paradigm and its parameters. The multi-layer feed-forward neural network approach consists of an input layer, one or several hidden layers and an output layer. Another approach is known as the partially recurrent neural network that can learn sequences as time evolves and responds to the same input pattern differently at different times, depending on the previous input patterns as well. None of these approaches is superior to the other in all cases; however, an additional dampened feedback, that possesses the characteristics of a dynamic memory, will improve the performance of both approaches.
Outlier Considerations: Outliers are a few observations that are not well fitted by the "best" available model. In practice, any observation with standardized residual greater than 2.5 in absolute value is a candidate for being an outlier. In such case, one must first investigate the source of data. If there is no doubt about the accuracy or veracity of the observation, then it should be removed, and the model should be refitted.
Whenever data levels are thought to be too high or too low for "business as usual", we call such points the outliers. A mathematical reason to adjust for such occurrences is that the majority of forecast techniques are based on averaging. It is well known that arithmetic averages are very sensitive to outlier values; therefore, some alteration should be made in the data before continuing. One approach is to replace the outlier by the average of the two sales levels for the periods, which immediately come before and after the period in question and put this number in place of the outlier. This idea is useful if outliers occur in the middle or recent part of the data. However, if outliers appear in the oldest part of the data, we may follow a second alternative, which is to simply throw away the data up to and including the outlier.
In light of the relative complexity of some inclusive but sophisticated forecasting techniques, we recommend that management go through an evolutionary progression in adopting new forecast techniques. That is to say, a simple forecast method well understood is better implemented than one with all inclusive features but unclear in certain facets.
Modeling and Simulation: Dynamic modeling and simulation is the collective ability to understand the system and implications of its changes over time including forecasting. System Simulation is the mimicking of the operation of a real system, such as the day-to-day operation of a bank, or the value of a stock portfolio over a time period. By advancing the simulation run into the future, managers can quickly find out how the system might behave in the future, therefore making decisions as they deem appropriate.
In the field of simulation, the concept of "principle of computational equivalence" has beneficial implications for the decision-maker. Simulated experimentation accelerates and replaces effectively the "wait and see" anxieties in discovering new insight and explanations of future behavior of the real system.
Probabilistic Models: Uses probabilistic techniques, such as Marketing Research Methods, to deal with uncertainty, gives a range of possible outcomes for each set of events. For example, one may wish to identify the prospective buyers of a new product within a community of size N. From a survey result, one may estimate the probability of selling p, and then estimate the size of sales as Np with some confidence level.
An Application: Suppose we wish to forecast the sales of new toothpaste in a community of 50,000 housewives. A free sample is given to 3,000 selected randomly, and then 1,800 indicated that they would buy the product.
Using the binomial distribution with parameters (3000, 1800/3000), the standard error is 27, and the expected sale is 50000(1800/3000) = 30000. The 99.7% confidence interval is within 3 times standard error 3(27) = 81 times the total population ratio 50000/3000; i.e., 1350. In other words, the range (28650, 31350) contains the expected sales.
Event History Analysis: Sometimes data on the exact time of a particular event (or events) are available, for example on a group of patients. Examples of events could include asthma attack; epilepsy attack; myocardial infections; hospital admissions. Often, occurrence (and non-occurrence) of an event is available on a regular basis, e.g., daily and the data can then be thought of as having a repeated measurements structure. An objective may be to determine whether any concurrent events or measurements have influenced the occurrence of the event of interest. For example, daily pollen counts may influence the risk of asthma attacks; high blood pressure might precede a myocardial infarction. One may use PROC GENMOD available in SAS for the event history analysis.
Predicting Market Response: As applied researchers in business and economics, faced with the task of predicting market response, we seldom know the functional form of the response. Perhaps market response is a nonlinear monotonic, or even a non-monotonic function of explanatory variables. Perhaps it is determined by interactions of explanatory variable. Interaction is logically independent of its components.
When we try to represent complex market relationships within the context of a linear model, using appropriate transformations of explanatory and response variables, we learn how hard the work of statistics can be. Finding reasonable models is a challenge, and justifying our choice of models to our peers can be even more of a challenge. Alternative specifications abound.
Modern regression methods, such as generalized additive models, multivariate adaptive regression splines, and regression trees, have one clear advantage: They can be used without specifying a functional form in advance. These data-adaptive, computer- intensive methods offer a more flexible approach to modeling than traditional statistical methods. How well do modern regression methods perform in predicting market response? Some perform quite well based on the results of simulation studies.
Delphi Analysis: Delphi Analysis is used in the decision making process, in particular in forecasting. Several "experts" sit together and try to compromise on something upon which they cannot agree.
System Dynamics Modeling: System dynamics (SD) is a tool for scenario analysis. Its main modeling tools are mainly the dynamic systems of differential equations and simulation. The SD approach to modeling is an important one for the following, not the least of which is that e.g., econometrics is the established methodology of system dynamics. However, from a philosophy of social science perspective, SD is deductive and econometrics is inductive. SD is less tightly bound to actuarial data and thus is free to expand out and examine more complex, theoretically informed, and postulated relationships. Econometrics is more tightly bound to the data and the models it explores, by comparison, are simpler. This is not to say the one is better than the other: properly understood and combined, they are complementary. Econometrics examines historical relationships through correlation and least squares regression model to compute the fit. In contrast, consider a simple growth scenario analysis; the initial growth portion of say, population is driven by the amount of food available. So there is a correlation between population level and food. However, the usual econometrics techniques are limited in their scope. For example, changes in the direction of the growth curve for a time population is hard for an econometrics model to capture.
Further Readings:
Delbecq, A., Group Techniques for Program Planning, Scott Foresman, 1975.
Gardner H.S., Comparative Economic Systems, Thomson Publishing, 1997.
Hirsch M., S. Smale, and R. Devaney, Differential Equations, Dynamical Systems, and an Introduction to Chaos, Academic Press, 2004.
Lofdahl C., Environmental Impacts of Globalization and Trade: A Systems Study, MIT Press, 2002.
Combination of Forecasts: Combining forecasts merges several separate sets of forecasts to form a better composite forecast. The main question is "how to find the optimal combining weights?" The widely used approach is to change the weights from time to time for a better forecast rather than using a fixed set of weights on a regular basis or otherwise.
All forecasting models have either an implicit or explicit error structure, where error is defined as the difference between the model prediction and the "true" value. Additionally, many data snooping methodologies within the field of statistics need to be applied to data supplied to a forecasting model. Also, diagnostic checking, as defined within the field of statistics, is required for any model which uses data.
Using any method for forecasting one must use a performance measure to assess the quality of the method. Mean Absolute Deviation (MAD), and Variance are the most useful measures. However, MAD does not lend itself to making further inferences, but the standard error does. For error analysis purposes, variance is preferred since variances of independent (uncorrelated) errors are additive; however, MAD is not additive.
Regression and Moving Average: When a time series is not a straight line one may use the moving average (MA) and break-up the time series into several intervals with common straight line with positive trends to achieve linearity for the whole time series. The process involves transformation based on slope and then a moving average within that interval. For most business time series, one the following transformations might be effective:
- slope/MA,
- log (slope),
- log(slope/MA),
- log(slope) - 2 log(MA).
Further Readings:
Armstrong J., (Ed.), Principles of Forecasting: A Handbook for Researchers and Practitioners, Kluwer Academic Publishers, 2001.
Arsham H., Seasonal and cyclic forecasting in small firm, American Journal of Small Business, 9, 46-57, 1985.
Brown H., and R. Prescott, Applied Mixed Models in Medicine, Wiley, 1999.
Cromwell J., W. Labys, and M. Terraza, Univariate Tests for Time Series Models, Sage Pub., 1994.
Ho S., M. Xie, and T. Goh, A comparative study of neural network and Box-Jenkins ARIMA modeling in time series prediction, Computers & Industrial Engineering, 42, 371-375, 2002.
Kaiser R., and A. Maravall, Measuring Business Cycles in Economic Time Series, Springer, 2001. Has a good coverage on Hodrick-Prescott Filter among other related topics.
Kedem B., K. Fokianos, Regression Models for Time Series Analysis, Wiley, 2002.
Kohzadi N., M. Boyd, B. Kermanshahi, and I. Kaastra , A comparison of artificial neural network and time series models for forecasting commodity prices, Neurocomputing, 10, 169-181, 1996.
Krishnamoorthy K., and B. Moore, Combining information for prediction in linear regression, Metrika, 56, 73-81, 2002.
Schittkowski K., Numerical Data Fitting in Dynamical Systems: A Practical Introduction with Applications and Software, Kluwer Academic Publishers, 2002. Gives an overview of numerical methods that are needed to compute parameters of a dynamical model by a least squares fit.
How to Do Forecasting by Regression Analysis
Introduction
Regression is the study of relationships among variables, a principal purpose of which is to predict, or estimate the value of one variable from known or assumed values of other variables related to it.
Variables of Interest: To make predictions or estimates, we must identify the effective predictors of the variable of interest: which variables are important indicators? and can be measured at the least cost? which carry only a little information? and which are redundant?
Predicting the Future Predicting a change over time or extrapolating from present conditions to future conditions is not the function of regression analysis. To make estimates of the future, use time series analysis.
Experiment: Begin with a hypothesis about how several variables might be related to another variable and the form of the relationship.
Simple Linear Regression: A regression using only one predictor is called a simple regression.
Multiple Regressions: Where there are two or more predictors, multiple regressions analysis is employed.
Data: Since it is usually unrealistic to obtain information on an entire population, a sample which is a subset of the population is usually selected. For example, a sample may be either randomly selected or a researcher may choose the x-values based on the capability of the equipment utilized in the experiment or the experiment design. Where the x-values are pre-selected, usually only limited inferences can be drawn depending upon the particular values chosen. When both x and y are randomly drawn, inferences can generally be drawn over the range of values in the sample.
Scatter Diagram: A graphical representation of the pairs of data called a scatter diagram can be drawn to gain an overall view of the problem. Is there an apparent relationship? Direct? Inverse? If the points lie within a band described by parallel lines, we can say there is a linear relationship between the pair of x and y values. If the rate of change is generally not constant, then the relationship is curvilinear.
The Model: If we have determined there is a linear relationship between t and y we want a linear equation stating y as a function of x in the form Y = a + bx + e where a is the intercept, b is the slope and e is the error term accounting for variables that affect y but are not included as predictors, and/or otherwise unpredictable and uncontrollable factors.
Least-Squares Method: To predict the mean y-value for a given x-value, we need a line which passes through the mean value of both x and y and which minimizes the sum of the distance between each of the points and the predictive line. Such an approach should result in a line which we can call a "best fit" to the sample data. The least-squares method achieves this result by calculating the minimum average squared deviations between the sample y points and the estimated line. A procedure is used for finding the values of a and b which reduces to the solution of simultaneous linear equations. Shortcut formulas have been developed as an alternative to the solution of simultaneous equations.
Solution Methods: Techniques of Matrix Algebra can be manually employed to solve simultaneous linear equations. When performing manual computations, this technique is especially useful when there are more than two equations and two unknowns.
Several well-known computer packages are widely available and can be utilized to relieve the user of the computational problem, all of which can be used to solve both linear and polynomial equations: the BMD packages (Biomedical Computer Programs) from UCLA; SPSS (Statistical Package for the Social Sciences) developed by the University of Chicago; and SAS (Statistical Analysis System). Another package that is also available is IMSL, the International Mathematical and Statistical Libraries, which contains a great variety of standard mathematical and statistical calculations. All of these software packages use matrix algebra to solve simultaneous equations.
Use and Interpretation of the Regression Equation: The equation developed can be used to predict an average value over the range of the sample data. The forecast is good for short to medium ranges.
Measuring Error in Estimation: The scatter or variability about the mean value can be measured by calculating the variance, the average squared deviation of the values around the mean. The standard error of estimate is derived from this value by taking the square root. This value is interpreted as the average amount that actual values differ from the estimated mean.
Confidence Interval: Interval estimates can be calculated to obtain a measure of the confidence we have in our estimates that a relationship exists. These calculations are made using t-distribution tables. From these calculations we can derive confidence bands, a pair of non-parallel lines narrowest at the mean values which express our confidence in varying degrees of the band of values surrounding the regression equation.
Assessment: How confident can we be that a relationship actually exists? The strength of that relationship can be assessed by statistical tests of that hypothesis, such as the null hypothesis, which are established using t-distribution, R-squared, and F-distribution tables. These calculations give rise to the standard error of the regression coefficient, an estimate of the amount that the regression coefficient b will vary from sample to sample of the same size from the same population. An Analysis of Variance (ANOVA) table can be generated which summarizes the different components of variation.
The Standard Error of Estimate, i.e. square root of error mean square, is a good indicator of the "quality" of a prediction model since it "adjusts" the Mean Error Sum of Squares (MESS) for the number of predictors in the model as follow:
If one keeps adding useless predictors to a model, the MESS will become less and less stable. R-squared is also influenced by the range of your dependent value; so, if two models have the same residual mean square but one model has a much narrower range of values for the dependent variable that model will have a higher R-squared. This explains the fact that both models will do as well for prediction purposes.
You may like using the Regression Analysis with Diagnostic Tools JavaScript to check your computations, and to perform some numerical experimentation for a deeper understanding of these concepts.
Predictions by Regression
The regression analysis has three goals: predicting, modeling, and characterization. What would be the logical order in which to tackle these three goals such that one task leads to and /or and justifies the other tasks? Clearly, it depends on what the prime objective is. Sometimes you wish to model in order to get better prediction. Then the order is obvious. Sometimes, you just want to understand and explain what is going on. Then modeling is again the key, though out-of-sample predicting may be used to test any model. Often modeling and predicting proceed in an iterative way and there is no 'logical order' in the broadest sense. You may model to get predictions, which enable better control, but iteration is again likely to be present and there are sometimes special approaches to control problems.The following contains the main essential steps during modeling and analysis of regression model building, presented in the context of an applied numerical example.
Formulas and Notations:
 = Sx /n
= Sx /n
This is just the mean of the x values. = Sy /n
= Sy /n
This is just the mean of the y values.- Sxx = SSxx = S(x(i)
-
 )2 = Sx2 - ( Sx)2 / n
)2 = Sx2 - ( Sx)2 / n - Syy = SSyy = S(y(i) -
 )2 = Sy2 - ( Sy) 2 / n
)2 = Sy2 - ( Sy) 2 / n - Sxy = SSxy = S(x(i) -
 )(y(i) -
)(y(i) -  ) = Sx ×y (Sx) × (Sy) / n
) = Sx ×y (Sx) × (Sy) / n - Slope m = SSxy / SSxx
- Intercept, b =
 - m .
- m . 
- y-predicted = yhat(i) = m×x(i) + b.
- Residual(i) = Error(i) = y yhat(i).
- SSE = Sres = SSres = SSerrors = S[y(i) yhat(i)]2.
- Standard deviation of residuals = s = Sres = Serrors = [SSres / (n-2)]1/2.
- Standard error of the slope (m) = Sres / SSxx1/2.
- Standard error of the intercept (b) = Sres[(SSxx + n.
 2) /(n × SSxx] 1/2.
2) /(n × SSxx] 1/2.
An Application: A taxicab company manager believes that the monthly repair costs (Y) of cabs are related to age (X) of the cabs. Five cabs are selected randomly and from their records we obtained the following data: (x, y) = {(2, 2), (3, 5), (4, 7), (5, 10), (6, 11)}. Based on our practical knowledge and the scattered diagram of the data, we hypothesize a linear relationship between predictor X, and the cost Y.
Now the question is how we can best (i.e., least square) use the sample information to estimate the unknown slope (m) and the intercept (b)? The first step in finding the least square line is to construct a sum of squares table to find the sums of x values (Sx), y values (Sy), the squares of the x values (Sx2), the squares of the x values (Sy2), and the cross-product of the corresponding x and y values (Sxy), as shown in the following table:
x
|
y
|
x2
|
xy
|
y2
|
|
2 |
2 |
4 |
4 |
4 |
|
3 |
5 |
9 |
15 |
25 |
|
4 |
7 |
16 |
28 |
49 |
|
5 |
10 |
25 |
50 |
100 |
|
6 |
11 |
36 |
66
|
121
|
|
SUM
|
20 |
35 |
90 |
163 |
299 |
The second step is to substitute the values of Sx, Sy, Sx2, Sxy, and Sy2 into the following formulas:
SSxy = Sxy (Sx)(Sy)/n = 163 - (20)(35)/5 = 163 - 140 = 23
SSxx = Sx2 (Sx)2/n = 90 - (20)2/5 = 90- 80 = 10
SSyy = Sy2 (Sy)2/n = 299 - 245 = 54
Use the first two values to compute the estimated slope:
Slope = m = SSxy / SSxx = 23 / 10 = 2.3
To estimate the intercept of the least square line, use the fact that the graph of the least square line always pass through ( ,
, 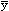 ) point, therefore,
) point, therefore,
The intercept = b = 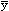 (m)(
(m)(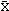 ) = (Sy)/ 5 (2.3) (Sx/5) = 35/5 (2.3)(20/5) = -2.2
) = (Sy)/ 5 (2.3) (Sx/5) = 35/5 (2.3)(20/5) = -2.2
Therefore the least square line is:
After estimating the slope and the intercept the question is how we determine statistically if the model is good enough, say for prediction. The standard error of slope is:
and its relative precision is measured by statistic
For our numerical example, it is:
which is large enough, indication that the fitted model is a "good" one.
You may ask, in what sense is the least squares line the "best-fitting" straight line to 5 data points. The least squares criterion chooses the line that minimizes the sum of square vertical deviations, i.e., residual = error = y - yhat:
x
Predictor |
-2.2+2.3x
y-predicted |
y
observed |
error
y |
squared
errors |
|
2 |
2.4 |
2 |
-0.4 |
0.16 |
|
3 |
4.7 |
5 |
0.3 |
0.09 |
|
4 |
7 |
7 |
0 |
0 |
|
5 |
9.3 |
10 |
0.7 |
0.49 |
|
6 |
11.6 |
11 |
-0.6 |
0.36 |
|
Sum=0 |
Sum=1.1 |
||||
Alternately, one may compute SSE by:
Notice that this value of SSE agrees with the value directly computed from the above table. The numerical value of SSE gives the estimate of variation of the errors s2:
The estimate the value of the error variance is a measure of variability of the y values about the estimated line. Clearly, we could also compute the estimated standard deviation s of the residuals by taking the square roots of the variance s2.
As the last step in the model building, the following Analysis of Variance (ANOVA) table is then constructed to assess the overall goodness-of-fit using the F-statistics:
Analysis of Variance Components
|
|||||
Source
|
DF |
Sum of Squares |
Mean Square |
F Value |
Prob > F |
Model |
1 |
52.90000 |
52.90000 |
144.273 |
0.0012 |
Error |
3 |
SSE = 1.1 |
0.36667 |
||
Total |
4 |
SSyy = 54 |
|||
For practical proposes, the fit is considered acceptable if the F-statistic is more than five-times the F-value from the F distribution tables at the back of your textbook. Note that, the criterion that the F-statistic must be more than five-times the F-value from the F distribution tables is independent of the sample size.
Notice also that there is a relationship between the two statistics that assess the quality of the fitted line, namely the T-statistics of the slope and the F-statistics in the ANOVA table. The relationship is:
This relationship can be verified for our computational example.
Predictions by Regression: After we have statistically checked the goodness of-fit of the model and the residuals conditions are satisfied, we are ready to use the model for prediction with confidence. Confidence interval provides a useful way of assessing the quality of prediction. In prediction by regression often one or more of the following constructions are of interest:
- A confidence interval for a single future value of Y corresponding to a chosen value of X.
- A confidence interval for a single pint on the line.
- A confidence region for the line as a whole.
Confidence Interval Estimate for a Future Value: A confidence interval of interest can be used to evaluate the accuracy of a single (future) value of y corresponding to a chosen value of X (say, X0). This JavaScript provides confidence interval for an estimated value Y corresponding to X0 with a desirable confidence level 1 - a.
Yp ± Se . tn-2, a/2 {1/n + (X0 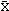 )2/ Sx}1/2
)2/ Sx}1/2
Confidence Interval Estimate for a Single Point on the Line: If a particular value of the predictor variable (say, X0) is of special importance, a confidence interval on the value of the criterion variable (i.e. average Y at X0) corresponding to X0 may be of interest. This JavaScript provides confidence interval on the estimated value of Y corresponding to X0 with a desirable confidence level 1 - a.
Yp ± Se . tn-2, a/2 { 1 + 1/n + (X0  )2/ Sx}1/2
)2/ Sx}1/2
It is of interest to compare the above two different kinds of confidence interval. The first kind has larger confidence interval that reflects the less accuracy resulting from the estimation of a single future value of y rather than the mean value computed for the second kind confidence interval. The second kind of confidence interval can also be used to identify any outliers in the data.
Confidence Region the Regression Line as the Whole: When the entire line is of interest, a confidence region permits one to simultaneously make confidence statements about estimates of Y for a number of values of the predictor variable X. In order that region adequately covers the range of interest of the predictor variable X; usually, data size must be more than 10 pairs of observations.
Yp ± Se { (2 F2, n-2, a) . [1/n + (X0  )2/ Sx]}1/2
)2/ Sx]}1/2
In all cases the JavaScript provides the results for the nominal (x) values. For other values of X one may use computational methods directly, graphical method, or using linear interpolations to obtain approximated results. These approximation are in the safe directions i.e., they are slightly wider that the exact values.