Optimización Lineal
Esta es la versión en Español del sitio Web principal en Inglés, el cual se encuentra disponible en:
Linear Programming
Un modelo de Optimización Matemática consiste en una función objetivo y un conjunto de restricciones en la forma de un sistema de ecuaciones o inecuaciones. Los modelos de optimización son usados en casi todas las áreas de toma de decisiones, como en ingeniería de diseño y selección de carteras financieras de inversión . Esta pagina web presenta ejemplos focalizados y estructurados para la formulación de problemas de optimización, diseño de la estrategia optima y herramientas de control de calidad que incluyen validación, verificación y análisis post-solución.
MENU
- Introducción y resumen
- Optimización: Programación Lineal (PL)
- Problema Dual: Construcción y Significado
- Manejo de Incertidumbres mediante Modelación de Escenarios
- El Método Simplex Clásico
- Programas Lineales Generales con Enteros
- Herramientas para el Proceso de Validación de Modelos
Para buscar el sitio, proba en Edicion | Encotrar en la página [Ctrl + f]. Escribi una palabra o frase en el espacio del diálogo. Por ejemplo "optimización" o "sensibilidad" Si el primer resultado de la palabra o la frase no es lo que vos buscabas, intenta con Encuentra Próximo.
Optimización: Programación Lineal (PL)
- Introducción y resumen
- Optimización
- Programación Lineal (PL)
- Proceso de Formulación de un Problema de PL y su Aplicación
- Método de Solución Gráfica
- Vínculo entre Programación Lineal y Sistemas de Ecuaciones
- Extensión a Mayores Dimensiones
- Ejemplo Numérico: el Problema del Transporte
- Conceptos y Técnicas de Aprendizaje Asistidos por Computadora
- Cómo Interpretar los Resultados del Paquete de Software LINDO
- Implementaciones de Computación con el Paquete WinQSB
- ¿Cómo Resolver un Sistema de Ecuaciones Lineales Utilizando un Software de PL?
Problema Dual
- Problema Dual: Construcción y Significado
- El Problema Dual del Problema del Carpintero y su Interpretación
- Errores de Redondeo cometido por los Gerentes
- Cálculo de los Precios Sombra
- Comportamiento de los Cambios en los Valores RHS del Valor Optimo
- Interpretación Incorrecta del Precio Sombra
- ¿El Precio Sombra es Siempre No Negativo?
- Precios Sombra Alternativos
Manejo de Incertidumbres mediante Modelación de Escenarios:
Análisis de Sensibilidad y Análisis de Especificidad
- Introducción
- Cálculo de Rangos de Sensibilidad para Problemas Pequeños
- Qué es la Regla del 100% (región de sensibilidad)
- Añadir una nueva restricción
- Suprimir una restricción
- Reemplazar una restricción
- Añadir una variable (por ejemplo, introducir un nuevo producto)
- Suprimir una variable (es decir, cancelar un producto)
- Problema de asignación óptima de recursos
- Determinación de la mínima utilidad neta del producto
- Indicadores de metas
- Cálculo de minimax y maximin en una sola corrida
- Situaciones de más por menos y menos por más
El Método Simplex Clásico
Programas Lineales Generales con Enteros
- Introducción
- Aplicación mixta de programación con enteros: restricciones "Y-O"
- Programas lineales con enteros 0 - 1
- Aplicaciones para formulación de presupuestos de inversiones
- Problemas de scheduling (planificación de turnos)
- Programación con restricciones no binarias
- Optimización combinatoria
- Programación no lineal
Herramientas para el Proceso de Validación de Modelos
- Introducción
- Ilimitación
- Soluciones Optimas Múltiples (soluciones óptimas Innumerables)
- No Solución (PL no-factible)
- Degeneración
- Redundancia entre las Restricciones
- PL sin Vértices
- PL con Soluciones Ilimitadas, y Soluciones Optimas Múltiples
- Sobre las Variables de Decisión Básicas y No-Básicas
- PL sin Ninguna Solución Interna
- PL sin Ninguna Solución Interna, y Limitada
- PL con Puntos Interiores como Soluciones Optimas
- La Solución Optima Generada por un Paquete de PL no es Obtenidas por Otro
- ¿La Tabla Optima del Simplex Proporciona una Solución Dual?
- La Conversión a la Forma Estándar Podría Distorsionar la Región de Factibilidad
- Remover las Restricciones de Igualdad Mediante la Sustitución Podría Cambiar el Problema
- Interpretación Errónea del Precio Sombra
- ¿Es el Precio Sombra Siempre no-Negativo?
- Precios Sombra Alternativos
- Situaciones Mas- por- Menos y Menos- por -Mas
Introducción y Resumen
Los problemas de toma de decisiones se pueden clasificar en dos categorías: modelos de decisión determinísticos y modelos de decisión probabilísticos. En los modelos deterministicos, las buenas decisiones se basan en sus buenos resultados. Se consigue lo deseado de manera "deterministica", es decir, libre de riesgo. Esto depende de la influencia que puedan tener los factores no controlables, en la determinación de los resultados de una decisión y también en la cantidad de información que el tomador de decisión tiene para controlar dichos factores.Aquellos que manejan y controlan sistemas de hombres y equipos se enfrentan al problema constante de mejorar (por ejemplo, optimizar) el rendimiento del sistema. El problema puede ser reducir el costo de operación y a la vez mantener un nivel aceptable de servicio, utilidades de las operaciones actuales, proporcionar un mayor nivel de servicio sin aumentar los costos, mantener un funcionamiento rentable cumpliendo a la vez con las reglamentaciones gubernamentales establecidas, o "mejorar" un aspecto de la calidad del producto sin reducir la calidad de otros aspectos. Para identificar la mejora del funcionamiento del sistema, se debe construir una representación sintética o modelo del sistema físico, que puede utilizarse para describir el efecto de una variedad de soluciones propuestas.
Un modelo puede considerarse como una entidad que captura la esencia de la realidad sin la presencia de la misma. Una fotografía es un modelo de la realidad ilustrada en la imagen. La presión arterial puede utilizarse como un modelo de la salud de una persona. Una campaña piloto de ventas puede utilizarse como un modelo de la respuesta de las personas a un nuevo producto. Por último, una ecuación matemática puede utilizarse como un modelo de la energía contenida en un determinado material. En cada caso, el modelo captura algún aspecto de la realidad que intenta representar.
Ya que un modelo sólo captura determinados aspectos de la realidad, su uso puede no ser apropiado en una aplicación en particular porque no captura los elementos correctos de la realidad. La temperatura es un modelo de las condiciones climáticas pero puede ser inapropiado si uno está interesado en la presión barométrica. Una foto de una persona es un modelo de la misma pero brinda poca información acerca de sus logros académicos. Una ecuación que predice las ventas anuales de un producto en particular es un modelo de ese producto pero tiene poca utilidad si lo que nos interesa es el costo de producción por unidad. Por lo tanto, la utilidad del modelo depende del aspecto de la realidad que representa.
Un modelo puede ser inadecuado aun cuando intenta capturar los elementos apropiados de la realidad si lo hace de una manera distorsionada o sesgada. Una ecuación que pronostica el volumen mensual de ventas puede ser exactamente lo que el gerente de ventas quiere pero podría generar grandes pérdidas si arroja constantemente cálculos de ventas altos. Un termómetro que lee de más (o de menos) tendría poca utilidad para realizar un diagnóstico médico. En consecuencia, un modelo útil es aquel que captura los elementos adecuados de la realidad con un grado aceptable de precisión.
Un modelo matemático es una ecuación, desigualdad o sistema de ecuaciones o desigualdades, que representa determinados aspectos del sistema físico representado en el modelo. Los modelos de este tipo se utilizan en gran medida en las ciencias físicas, en el campo de la ingeniería, los negocios y la economía.
Un modelo ofrece al analista una herramienta que puede manipular en su análisis del sistema en estudio, sin afectar al sistema en sí. Por ejemplo, supóngase que se ha desarrollado un modelo matemático para predecir las ventas anuales como una función del precio de venta unitario. Si se conoce el costo de producción por unidad, se pueden calcular con facilidad las utilidades anuales totales para cualquier precio de venta. Para determinar el precio de venta que arrojará las utilidades totales máximas, se pueden introducir en el modelo distintos valores para el precio de venta, uno a la vez, determinando las ventas resultantes y calculando las utilidades anuales totales para cada valor de precio de venta examinado. Mediante un proceso de prueba y error, el analista puede determinar el precio de venta que maximizará las utilidades anuales totales.
Lo ideal sería que si el modelo matemático es una representación válida del rendimiento del sistema, mediante la aplicación de las técnicas analíticas adecuadas, la solución obtenida a partir del modelo debería ser también la solución para el problema del sistema. Así, la efectividad de los resultados de la aplicación de cualquier técnica operativa es en gran medida una función del grado en el cual el modelo representa al sistema en estudio.
A fin de definir las condiciones que nos conducirán a la solución del problema del sistema, el analista primero debe identificar un criterio según el cual se podrá medir el sistema. Este criterio a menudo se denomina medida del rendimiento del sistema o medida de efectividad. En aplicaciones empresariales, la medida de efectividad generalmente son los costos o las utilidades, mientras que en aplicaciones gubernamentales esta medida generalmente se define en términos de un índice costo/beneficio.
El modelo matemático que describe el comportamiento de la medida de efectividad se denomina función objetivo. Si la función objetivo es describir el comportamiento de la medida de efectividad, debe capturar la relación entre esa medida y aquellas variables que hacen que dicha medida fluctúe. Las variables del sistema pueden categorizarse en variables de decisión y parámetros. Una variable de decisión es una variable que puede ser directamente controlada por el decisor. También existen algunos parámetros cuyos valores pueden ser inciertos para el decisor. Esto requiere un análisis de sensibilidad después de descubrir la mejor estrategia. En la práctica, resulta casi imposible capturar la relación precisa entre todas las variables del sistema y la medida de efectividad a través de una ecuación matemática. En cambio, el analista de IO/CA debe tratar de identificar aquellas variables que afectan en mayor grado la medida de efectividad y luego debe intentar definir de manera lógica la relación matemática entre estas variables y la medida de efectividad. Esta relación matemática es la función objetivo que se emplea para evaluar el rendimiento del sistema en estudio.
La formulación de una función objetivo que tenga sentido normalmente es una tarea tediosa y frustrante. Los intentos de desarrollo de una función objetivo pueden terminar en un fracaso. Esto puede darse porque el analista elige el conjunto incorrecto de variables para incluir en el modelo o bien, si el conjunto es el adecuado, porque no identifica correctamente la relación entre estas variables y la medida de efectividad. En un nuevo intento, el analista trata de descubrir las variables adicionales que podrían mejorar su modelo descartando aquellas que parecen tener poca o ninguna relevancia. No obstante, sólo se puede determinar si estos factores realmente mejoran el modelo una vez realizadas la formulación y prueba de nuevos modelos que incluyan las variables adicionales. Todo el proceso de selección y rechazo de variables puede requerir reiteraciones múltiples hasta desarrollar una función objetivo satisfactoria. En cada iteración, el analista espera lograr alguna mejora en el modelo, aunque no siempre se tiene tanta buena suerte. Por lo general, el éxito final es precedido por una serie de fracasos frustrantes y pequeños progresos.
En cada etapa del proceso de desarrollo, el analista debe evaluar la correspondencia o validez del modelo. Normalmente se emplean dos criterios para realizar esta determinación. El primero implica la experimentación del modelo: someter el modelo a una serie de condiciones y registrar los valores asociados de la medida de efectividad dada por el modelo en cada caso. Si la medida de efectividad varía de manera antinatural con una sucesión de condiciones de entrada, es posible que la función objetivo no sea válida. Por ejemplo, supóngase que se desarrolla un modelo destinado a calcular el valor de mercado de viviendas unifamiliares. El modelo debe expresar el valor de mercado en dólares como una función de la superficie cubierta en pies cuadrados, cantidad de dormitorios, cantidad de baños y tamaño del lote. Después de desarrollar el modelo, el analista lo aplica a la tasación de distintas viviendas, con distintos valores para las características mencionadas y descubre que el valor de mercado desciende a medida que aumenta la superficie cubierta expresada en pies cuadrados. Dado que este resultado no concuerda con la realidad, el analista cuestionaría la validez del modelo. Por otro lado, supóngase que el modelo es tal que el valor de las viviendas es una función creciente de cada una de las cuatro características citadas, como generalmente es de esperar. Si bien este resultado es alentador, no necesariamente implica que el modelo es una representación válida de la realidad, dado que la tasa de aumento de cada variable puede ser excesivamente alta o baja. La segunda etapa de la validación del modelo requiere una comparación de los resultados del modelo con los resultados obtenidos en la realidad.
Optimización
La humanidad hace tiempo que busca, o profesa buscar, mejores maneras de realizar las tareas cotidianas de la vida. A lo largo de la historia de la humanidad, se puede observar la larga búsqueda de fuentes más efectivas de alimentos al comienzo y luego de materiales, energía y manejo del entorno físico. Sin embargo, relativamente tarde en la historia de la humanidad, comenzaron a formularse ciertas clases de preguntas generales de manera cuantitativa, primero en palabras y después en notaciones simbólicas. Un aspecto predominante de estas preguntas generales era la búsqueda de lo "mejor" o lo "óptimo". Generalmente, los gerentes buscan simplemente lograr alguna mejora en el nivel de rendimiento, es decir, un problema de "búsqueda de objetivo". Cabe destacar que estas palabras normalmente no tienen un significado precisoSe han realizado grandes esfuerzos por describir complejas situaciones humanas y sociales. Para tener significado, esto debería escribirse en una expresión matemática que contenga una o más variables, cuyos valores deben determinarse. La pregunta que se formula, en términos generales, es qué valores deberían tener estas variables para que la expresión matemática tenga el mayor valor numérico posible (maximización) o el menor valor numérico posible (minimización). A este proceso general de maximización o minimización se lo denomina optimización.
La optimización, también denominada programación matemática, sirve para encontrar la respuesta que proporciona el mejor resultado, la que logra mayores ganancias, mayor producción o felicidad o la que logra el menor costo, desperdicio o malestar. Con frecuencia, estos problemas implican utilizar de la manera más eficiente los recursos, tales como dinero, tiempo, maquinaria, personal, existencias, etc. Los problemas de optimización generalmente se clasifican en lineales y no lineales, según las relaciones del problema sean lineales con respecto a las variables. Existe una serie de paquetes de software para resolver problemas de optimización. Por ejemplo, LINDO o WinQSB resuelven modelos de programas lineales y LINGO y What'sBest! resuelven problemas lineales y no lineales.
La Programación Matemática, en general, aborda el problema de determinar asignaciones óptimas de recursos limitados para cumplir un objetivo dado. El objetivo debe representar la meta del decisor. Los recursos pueden corresponder, por ejemplo, a personas, materiales, dinero o terrenos. Entre todas las asignaciones de recursos admisibles, queremos encontrar la/s que maximiza/n o minimiza/n alguna cantidad numérica tal como ganancias o costos.
El objetivo de la optimización global es encontrar la mejor solución de modelos de decisiones difíciles, frente a las múltiples soluciones locales.
Programación Lineal (PL)
La programación lineal muchas veces es uno de los temas preferidos tanto de profesores como de alumnos. La capacidad de introducir la PL utilizando un abordaje gráfico, la facilidad relativa del método de solución, la gran disponibilidad de paquetes de software de PL y la amplia gama de aplicaciones hacen que la PL sea accesible incluso para estudiantes con poco conocimiento de matemática. Además, la PL brinda una excelente oportunidad para presentar la idea del análisis what-if o análisis de hipótesis ya que se han desarrollado herramientas poderosas para el análisis de post optimalidad para el modelo de PL.La Programación Lineal (PL) es un procedimiento matemático para determinar la asignación óptima de recursos escasos. La PL es un procedimiento que encuentra su aplicación práctica en casi todas las facetas de los negocios, desde la publicidad hasta la planificación de la producción. Problemas de transporte, distribución, y planificación global de la producción son los objetos más comunes del análisis de PL. La industria petrolera parece ser el usuario más frecuente de la PL. Un gerente de procesamiento de datos de una importante empresa petrolera recientemente calculó que del 5% al 10% del tiempo de procesamiento informático de la empresa es destinado al procesamiento de modelos de PL y similares.
La programación lineal aborda una clase de problemas de programación donde tanto la función objetivo a optimizar como todas las relaciones entre las variables correspondientes a los recursos son lineales. Este problema fue formulado y resuelto por primera vez a fines de la década del 40. Rara vez una nueva técnica matemática encuentra una gama tan diversa de aplicaciones prácticas de negocios, comerciales e industriales y a la vez recibe un desarrollo teórico tan exhaustivo en un período tan corto. Hoy en día, esta teoría se aplica con éxito a problemas de presupuestos de capital, diseño de dietas, conservación de recursos, juegos de estrategias, predicción de crecimiento económico y sistemas de transporte. Recientemente la teoría de la programación lineal también contribuyó a la resolución y unificación de diversas aplicaciones.
Es importante que el lector entienda desde el comienzo que el término "programación" tiene un significado distinto cuando se refiere a Programación Lineal que cuando hablamos de Programación Informática. En el primer caso, significa planificar y organizar mientras que en el segundo caso, significa escribir las instrucciones para realizar cálculos. La capacitación en una clase de programación tiene muy poca relevancia directa con la otra clase de programación. De hecho, el término "programación lineal" se acuñó antes de que la palabra programación se relacionara con el software de computación. A veces se evita esta confusión utilizando el término optimización lineal como sinónimo de programación lineal.
Cualquier problema de PL consta de una función objetivo y un conjunto de restricciones. En la mayoría de los casos, las restricciones provienen del entorno en el cual usted trabaja para lograr su objetivo. Cuando usted quiere lograr el objetivo deseado, se dará cuenta de que el entorno fija ciertas restricciones (es decir, dificultades, limitaciones) para cumplir con su deseo (vale decir, el objetivo). Es por eso que las religiones, como el Budismo entre otras, prescriben vivir una vida abstemia. Sin deseo, no hay dolor. ¿Puede usted seguir este consejo con respecto a su objetivo de negocios?
Qué es una función: una función es una cosa que hace algo. Por ejemplo, una máquina de moler café es una función que transforma los granos de café en polvo. La función (objetivo) traza, traduce el dominio de entrada (denominado región factible) en un rango de salida con dos valores finales denominados valores máximo y mínimo.
Cuando se formula un problema de toma de decisiones como un programa lineal, se deben verificar las siguientes condiciones:
- 1. La función objetivo debe ser lineal. Vale decir que se debe verificar que todas las variables estén elevadas a la primera potencia y que sean sumadas o restadas (no divididas ni multiplicadas);
- 2. El objetivo debe ser ya sea la maximización o minimización de una función lineal. El objetivo debe representar la meta del decisor; y
- 3. Las restricciones también deben ser lineales. . Asimismo, la restricción debe adoptar alguna de las siguientes formas ( £, ³, O =, es decir que las restricciones de PL siempre están cerradas).
Por ejemplo, el siguiente problema no es un problema de PL: Max X, sujeta a < 1. Este problema tan sencillo no tiene solución.
Como siempre, se debe tener cuidado al categorizar un problema de optimización como un problema de PL. ¿El siguiente problema es un problema de PL?
Max X2
sujeta a:
X1 + X2 £ 0
X12 - 4 £ 0
Aunque la segunda restricción parece "como si" fuera una restricción no lineal, esta restricción puede escribirse también de la siguiente forma:
X1 ³ -2, y X2 £ 2.
En consecuencia, el problema es de hecho un problema de PL.
Para la mayoría de los problemas de PL, podemos decir que existen dos tipos importantes de objetos: en primer lugar, los recursos limitados, tales como terrenos, capacidad de planta, o tamaño de la fuerza de ventas; en segundo lugar, las actividades, tales como "producir acero con bajo contenido de carbono", y "producir acero con alto contenido de carbono". Cada actividad consume o probablemente contribuye cantidades adicionales de recursos. Debe haber una función objetivo, es decir, una manera de discriminar una mala de una buena o una mejor decisión. El problema es determinar la mejor combinación de niveles de actividades, que no utilice más recursos de los disponibles. Muchos gerentes se enfrentan a esta tarea todos los días. Afortunadamente, el software de programación lineal ayuda a determinar esto cuando se ingresa un modelo bien formulado.
El método Simplex es un algoritmo de solución muy utilizado para resolver programas lineales. Un algoritmo es una serie de pasos para cumplir con una tarea determinada.
Proceso de Formulación de un Problema de PL y su Aplicación
Para formular un problema de PL, recomiendo seguir los siguientes lineamientos generales después de leer con atención el enunciado del problema varias veces.Todo programa lineal consta de cuatro partes: un conjunto de variables de decisión, los parámetros, la función objetivo y un conjunto de restricciones. Al formular un determinado problema de decisión en forma matemática, debe practicar la comprensión del problema (es decir, formular un Modelo Mental) leyendo detenidamente una y otra vez el enunciado del problema. Mientras trata de comprender el problema, formúlese las siguientes preguntas generales:
- ¿Cuáles son las variables de decisión? Es decir, ¿cuáles con las entradas controlables? Defina las variables de decisión con precisión utilizando nombres descriptivos. Recuerde que las entradas controlables también se conocen como actividades controlables, variables de decisión y actividades de decisión.
- Cuáles son los parámetros? Vale decir ¿cuáles son las entradas no controlables? Por lo general, son los valores numéricos constantes dados. Defina los parámetros con precisión utilizando nombres descriptivos.
- ¿Cuál es el objetivo? ¿Cuál es la función objetivo? Es decir, ¿qué quiere el dueño del problema? ¿De qué manera se relaciona el objetivo con las variables de decisión del dueño del problema? ¿Es un problema de maximización o minimización? El objetivo debe representar la meta del decisor.
- ¿Cuáles son las restricciones? Es decir, ¿qué requerimientos se deben cumplir? ¿Debería utilizar un tipo de restricción de desigualdad o igualdad? ¿Cuáles son las conexiones entre las variables? Escríbalas con palabras antes de volcarlas en forma matemática.
Recuerde que la región factible tiene poco o nada que ver con la función objetivo (minim. o maxim.). Estas dos partes en cualquier formulación de PL generalmente provienen de dos fuentes distintas. La función objetivo se establece para cumplir con el deseo (objetivo) del decisor mientras que las restricciones que forman la región factible generalmente provienen del entorno del decisor que fija algunas limitaciones / condiciones para lograr su objetivo.
A continuación, se incluye un problema ilustrativo muy sencillo. Sin embargo, el abordaje del problema es igual para una gran variedad de problemas de toma de decisión, mientras que el tamaño o la complejidad pueden variar. El primer ejemplo es un problema de mix de productos y el segundo es un problema de mezcla.
El Problema del Carpintero
Durante un par de sesiones de brain-storming con un carpintero (nuestro cliente), éste nos comunica que sólo fabrica mesas y sillas y que vende todas las mesas y las sillas que fabrica en un mercado. Sin embargo, no tiene un ingreso estable y desea optimizar esta situación.El objetivo es determinar cuántas mesas y sillas debería fabricar para maximizar sus ingresos netos. Comenzamos concentrándonos en un horizonte de tiempo, es decir, un plazo de planificación, , para revisar nuestra solución semanalmente, si fuera necesario. Para saber más acerca de este problema, debemos ir al negocio del carpintero y observar lo que sucede y medir lo que necesitamos para para formular (para crear un modelo de) su problema. Debemos confirmar que su objetivo es maximizar sus ingresos netos. Debemos comunicarnos con el cliente.
El problema del carpintero se trata de determinar cuántas mesas y sillas debe fabricar por semana; pero primero se debe establecer una función objetivo La función objetivo es: 5X1 + 3X2, donde X1 y X2 representan la cantidad de mesas y sillas; y 5 y 3 representan los ingresos netos (por ejemplo, en dólares o décimas de dólares) de la venta de una mesa y una silla, respectivamente. Los factores limitantes, que normalmente provienen del exterior, son las limitaciones de la mano de obra (esta limitación proviene de la familia del carpintero) y los recursos de materia prima (esta limitación proviene de la entrega programada). Se miden los tiempos de producción requeridos para una mesa y una silla en distintos momentos del día y se calculan en 2 horas y 1 hora, respectivamente. Las horas laborales totales por semana son sólo 40. La materia prima requerida para una mesa y una silla es de 1 y 2 unidades, respectivamente. El abastecimiento total de materia prima es de 50 unidades por semana. En consecuencia, la formulación de PL es la siguiente:
Maximizar 5 X1 + 3 X2
Sujeta a:
2 X1 + X2 £ 40 restricción de mano de obra
X1 + 2 X2 £ 50 restricción de materiales
tanto X1 como X2 son no negativas.
Este es un modelo matemático para el problema del carpintero. Las variables de decisión, es decir, las entradas controlables son X1, y X2. La salida o el resultado de este modelo son los ingresos netos totales 5 X1 + 3 X2. Todas las funciones empleadas en este modelo son lineales (las variables de decisión están elevadas a la primera potencia). El coeficiente de estas restricciones se denomina denomina Factores Tecnológicos (matriz). El período de revisión es de una semana, un período conveniente dentro del cual es menos probable que cambien (fluctúen) las entradas controlables (todos los parámetros tales como 5, 50, 2,..). Incluso en un plazo de planificación tan corto, debemos realizar el análisis what-if o de hipótesis para responder a cualquier cambio en estas entradas a los efectos de controlar el problema, es decir, actualizar la solución prescripta.
Nótese que dado que el Carpintero no va a ir a la quiebra al final del plazo de planificación, agregamos las condiciones que tanto X1 como X2 deben ser no negativas en lugar de los requerimientos que X1 y X2 deben ser números enteros positivos. Recuerde que las condiciones de no negatividad también se denominan "restricciones implícitas". Nuevamente, un Programa Lineal funcionaría bien para este problema si el Carpintero continúa fabricando estos productos. Los artículos parciales simplemente se contarían como trabajos en proceso y finalmente se transformarían en productos terminados, en la siguiente semana.
Podemos intentar resolver X1 y X2 enumerando posibles soluciones para cada una y seleccionado el par (X1, X2) que maximice 5X1 + 3X2 (los ingresos netos). Sin embargo, lleva mucho tiempo enumerar todas las alternativas posibles y si no se enumeran todas las alternativas, no podemos estar seguros de que el par seleccionado (como una solución) es la mejor de todas las alternativas. Otras metodologías preferidas (más eficientes y efectivas), conocidas como las Técnicas de Soluciones de Programación Lineal están disponibles en el mercado en más de 4000 paquetes de software de todo el mundo.
La solución óptima, es decir, la estrategia óptima, , es establecer X1 = 10 mesas y X2 = 20 sillas. Programamos las actividades semanales del carpintero para que fabrique 10 mesas y 20 sillas. Con esta estrategia (óptima), los ingresos netos son de US$110. Esta . Esta solución prescripta sorprendió al carpintero dado que debido a los mayores ingresos netos provenientes de la venta de una mesa (US$5), el solía fabricar más mesas que sillas.
¿Contratar o no contratar a un ayudante? Supóngase que el carpintero pudiera contratar a un ayudante a un costo de US$2 por hora (adicionales $2) ¿Le conviene al carpintero contratar a un ayudante? En caso afirmativo, ¿por cuántas horas?
X3 es la cantidad de horas extra, entonces el problema modificado es:
Maximizar 5 X1 + 3 X2 - 2 X3
Sujeta a:
2 X1 + X2 £ 40 + X3 restricción de la mano de obra con horas adicionales desconocidas
X1 + 2 X2 £ 50 restricción de materiales
En esta nueva condición, veremos que la solución óptima es X1 = 50, X2 = 0, X3 = 60, con ingresos netos óptimos de US$130. Por lo tanto, el carpintero debería contratar a un ayudante por 60 horas. ¿Qué pasaría si sólo lo contrata por 40 horas? La respuesta a esta pregunta y a otros tipos de preguntas del estilo "qué pasaría si" (what-if) se estudia en la sección sobre análisis de sensibilidad en este sitio Web.
Un Problema de Mezcla
El taller de Joe se especializa en cambios de aceite del motor y regulacion del sistema electrico. El beneficio por cambio del aceite es $7 y de $15 por regulacion. Joe tiene un cliente fijo con cuya flota, le garantiza 30 cambios de aceite por semana. Cada cambio de aceite requiere de 20 minutos de trabajo y $8 de insumos. Una regulacion toma una hora de trabajo y gasta $15 en insumos. Joe paga a los mecanicos $10 por hora de trabajo y emplea actualmente a dos de ellos, cada uno de los cuales labora 40 horas por semana. Las compras de insumos alcanzan un valor de $1.750 semanales. Joe desea maximizar el beneficio total. Formule el problema.
Esto es una pregunta de programación linear. Una porción de un cambio del aceite o del ajuste no es factible.
X1 = Cambios del aceite, ajuste
X2 = Ajuste
Maximizar 7X1 + 15X2
Sujeta a:
X1 ³ 30 Cuenta De la Flota
20X1 + 60X2 £ 4800 De trabajo tiempo
8X1 + 15X2 £ 1750 Primas Materias
X1 ³ 0, X2 ³ 0.
El coste de trabajo de $10 por hora no se requiere para formatar el problema desde el beneficio por cambio del aceite y el ajuste toma en la consideración el coste de trabajo.
Otras Aplicaciones Comunes de PL
La programación lineal es una herramienta poderosa para seleccionar alternativas en un problema de decisión y por consiguiente se aplica en una gran variedad de entornos de problemas. La cantidad de aplicaciones es tan alta que sería imposible enumerarlas todas. A continuación, indicamos algunas de las principales aplicaciones que cubren las áreas funcionales más importantes de una organización empresarial.Finanzas: el problema del inversor podría ser un problema de selección del mix de su cartera de inversiones. En general, la variedad de carteras puede ser mucho mayor que lo que indica el ejemplo y se pueden agregar muchas más restricciones distintas. Otro problema de decisión implica determinar la combinación de métodos de financiación para una cantidad de productos cuando existe más de un método de financiación disponible. El objetivo puede ser maximizar las ganancias totales cuando las ganancias de un producto determinado dependen del método de financiación. Por ejemplo, se puede financiar con fondos internos, con deuda a corto plazo o con financiación intermedia (créditos amortizados). Puede haber limitaciones con respecto a la disponibilidad de cada una de las opciones de financiación, así como también restricciones financieras que exijan determinadas relaciones entre las opciones de financiación a los efectos de satisfacer los términos y condiciones de los préstamos bancarios o financiación intermedia. También puede haber límites con respecto a la capacidad de producción de los productos. Las variables de decisión serían la cantidad de unidades que deben ser financiadas por cada opción de financiación.
Administración de Producción y Operaciones: muchas veces en las industrias de proceso, una materia prima en particular puede transformarse en una gran variedad de productos. Por ejemplo, en la industria petrolera, el crudo puede refinarse para producir nafta, kerosene, aceite para calefaccionar y distintas clases de aceite para motor. Según el margen de ganancia actual de cada producto, el problema es determinar la cantidad que se debería fabricar de cada producto. Esta decisión está sujeta a numerosas restricciones tales como límites de las capacidades de diversas operaciones de refinado, disponibilidad de materia prima, demandas de cada producto y políticas gubernamentales con respecto a la fabricación de determinados productos. En la industria de productos químicos y de procesamiento de alimentos existen problemas similares.
Recursos Humanos: los problemas de planificación de personal también se pueden analizar con programación lineal. Por ejemplo, en la industria telefónica, la demanda de servicios de personal de instalación / reparación son estacionales. El problema es determinar la cantidad de personal de instalación / reparación y reparación de líneas que debemos tener incorporada en la fuerza laboral por cada mes a fin de minimizar los costos totales de contratación, despido, horas extras y salarios en horas ordinarias. El conjunto de restricciones comprende restricciones con respecto a la demanda de servicio que se debe satisfacer, uso de horas extra, acuerdos con los sindicatos y la disponibilidad de personal calificado para contratar. Este ejemplo es opuesto a la hipótesis de divisibilidad. Sin embargo, los niveles de fuerza laboral de cada mes normalmente son lo suficientemente altos como para poder redondear al número entero más cercano sin problemas, siempre y cuando no se violen las restricciones.
Marketing: se puede utilizar la programación lineal para determinar el mix adecuado de medios de una campaña de publicidad. Supóngase que los medios disponibles son radio, televisión y diarios. El problema es determinar cuántos avisos hay que colocar en cada medio. Por supuesto que el costo de colocación de un aviso depende del medio elegido. El objetivo es minimizar el costo total de la campaña publicitaria, sujeto a una serie de restricciones. Dado que cada medio puede proporcionar un grado diferente de exposición a la población meta, puede haber una cota inferior con respecto a la exposición de la campaña. Asimismo, cada medio puede tener distintos ratings de eficiencia para producir resultados deseables y por consiguiente puede haber una cota inferior con respecto a la eficiencia. Además, puede haber límites con respecto a la disponibilidad para publicar en cada medio.
Distribución: otra aplicación de programación lineal es el área de la distribución. Considere un caso en el que existen m fábricas que deben enviar productos a n depósitos. Una determinada fábrica podría realizar envíos a cualquier cantidad de depósitos. Dado el costo del envío de una unidad del producto de cada fábrica a cada depósito, el problema es determinar el patrón de envío (cantidad de unidades que cada fábrica envía a cada depósito) que minimice los costos totales. Este decisión está sujeta a restricciones que exigen que cada fábrica no pueda enviar más productos de los que tiene capacidad para producir.
Método de Solución Gráfica
Dado que somos una especie visual (especialmente la cultura estadounidense), debido a nuestro sistema educativo, muchas de las herramientas de enseñanza escolar utilizadas en la actualidad son de naturaleza gráfica. Les enseñamos a leer mostrándoles figuras de las cosas. Les enseñamos a contar mostrándoles el orden de los números. En consecuencia, nuestros receptores visuales se agudizan a expensas de otras funciones cognitivas. También he descubierto que las personas de negocios responden mejor a los gráficos y a los cuadros que a los números.Procedimiento para el Método Gráfico de Solución de Problemas de PL:
- ¿El problema es un problema de PL? La respuesta es afirmativa si y sólo si:
Todas las variables están elevadas a la primera potencia y son sumadas o restadas (no dividas ni multiplicadas). La restricción debe adoptar alguna de las siguientes formas (£, ³, o =, es decir que las restricciones de PL siempre están cerradas), y el objetivo debe ser de maximización o minimización.
Por ejemplo, el siguiente problema no es un problema de PL: Max X, sujeta a <. Este problema tan sencillo no tiene solución.
- ¿Puedo utilizar el método gráfico? La respuesta es afirmativa si la cantidad de variables de decisión es 1 o 2.
- Utilice papel milimetrado. Grafique cada restricción, una por una, como si fueran igualdades (como si todo £ y ³, es = ) y luego trace la línea.
- A medida que se crea cada línea, divida la región en 3 partes con respecto a cada línea. Para identificar la región factible para esta restricción en particular, elija un punto en cualquier lado de la línea y coloque sus coordenadas en la restricción, si satisface la condición, este lado es factible, de lo contrario el otro lado es factible. En el caso de restricciones de igualdad, sólo los puntos sobre la línea son factibles.
- Elimine los lados que no son factibles.
Una vez graficadas todas las restricciones, debe generarse una región factible no vacía (convexa), salvo que el problema sea no factible.
- Cree (como mínimo) dos líneas de igual valor desde la función objetivo, fijando la función objetivo en dos números distintos cualquiera. Grafique las líneas resultantes. Al mover estas líneas paralelas, encontrará el vértice óptimo (punto extremo), si es que existe.
En general, si la región factible se encuentra dentro del primer cuadrante del sistema de coordenadas (es decir si X1 y X2 ³ 0), entonces, para los problemas de maximización, usted debe mover la función objetivo de igual valor (función iso) paralela a sí misma lejos del punto de origen (0, 0), como mínimo, teniendo a la vez un punto en común con la región factible. Sin embargo, para los problemas de minimización, debe realizar lo opuesto, es decir, mover la función objetivo de igual valor (función iso) paralela a sí misma acercándola al punto de origen, a su vez teniendo como mínimo un punto en común con la región factible. El punto común proporciona la solución óptima.
Recuerde que las restricciones de PL proporcionan los vértices y las esquinas. Un vértice es la intersección de 2 líneas o en general, n hiperplanos en problemas de PL con n variables de decisión. Una esquina es un vértice que además es factible.
Un Ejemplo Numérico: El Problema del Carpintero
Maximizar 5 X1 + 3 X2
Sujeta a:
2 X1 + X2 £ 40
X1 + 2 X2 £ 50
and both X1, X2 are non-negative.
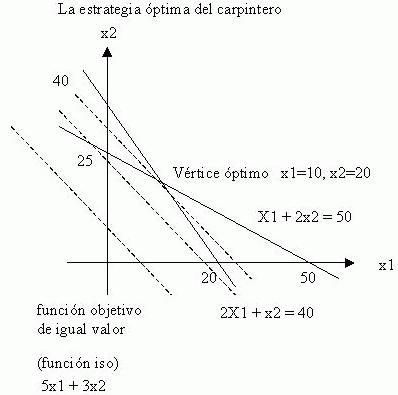
Nota: Existe una alternativa del abordaje de la función objetivo de igual valor (función iso) con problemas que tienen pocas restricciones y una región factible acotada. Primero busque todas las esquinas, también llamadas puntos extremos. Luego, evalúe la función objetivo en los puntos extremos para llegar al valor óptimo y a la solución óptima.
Por ejemplo, en el problema del carpintero, la región factible convexa proporciona los puntos extremos con las coordenadas que figuran en la siguiente Tabla:
| Elecciones del Decisor | Coordenadas de los Puntos Extremos | Función de los Ingresos Netos |
|---|---|---|
| Cantidad de Mesas o Sillas | X1, X2 | 5 X1 + 3 X2 |
| No fabricar ninguna mesa ni silla | 0, 0 | 0 |
| Fabricar todas la mesas posibles | 20, 0 | 100 |
| Fabricar todas las sillas posibles | 0, 25 | 75 |
| Fabricar una combinación de productos | 10, 20 | 110 |
Dado que el objetivo es maximizar, de la tabla anterior surge que el valor óptimo es 110, el cual se obtiene si el carpintero sigue la estrategia óptima de X1 = 10 y X2 = 20.
Si un programa lineal tiene una región factible acotada no vacía, la solución óptima es siempre uno de los puntos extremos. .
La prueba de esta afirmación surge de los resultados de los siguientes dos hechos:
Hecho N° 1: La región factible de cualquier programa lineal es siempre un conjunto convexo.
Debido a que todas las restricciones son lineales, la región factible (R.F.) es un polígono. Además, este polígono es un conjunto convexo. En cualquier problema de PL que tenga más de dos dimensiones, los límites de la región factible son partes de los hiperplanos, y la región factible en este caso se denomina poliedro y también es convexa. Un conjunto convexo es aquel en el cual si se eligen dos puntos factibles, todos los puntos en el segmento de la línea recta que une estos dos puntos también son factibles. La prueba de que la región factible de los programas lineales son siempre conjuntos convexos surge por contradicción. Las siguientes figuras ilustran ejemplos de los dos tipos de conjuntos: un conjunto no convexo y un conjunto convexo.
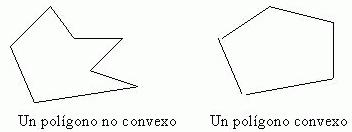
El conjunto de la región factible en cualquier programa lineal se denomina poliedro y si está acotado se denomina politopo.
Hecho N° 2: El valor iso de una función objetivo de un programa lineal es siempre una función lineal.
Este hecho surge de la naturaleza de la función objetivo de cualquier problema de PL. Las siguientes figuras ilustran las dos clases típicas de funciones objetivo de igual valor (función iso).
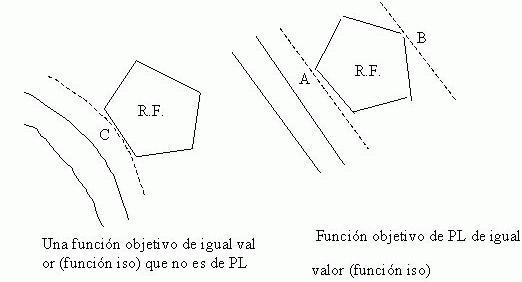
De la combinación de los dos hechos expresados arriba surge que si un programa lineal tiene una región factible acotada no vacía, la solución óptima es siempre uno de los puntos extremos.
Para superar la deficiencia del método gráfico, utilizaremos esta conclusión útil y práctica en el desarrollo de un método algebraico aplicable a problemas de PL multidimensionales.
La convexidad de la región factible de los programas lineales facilita la resolución de problemas de PL. Debido a esta propiedad y a la linealidad de la función objetivo, la solución es siempre uno de los vértices. Asimismo, dado que la cantidad de vértices es limitada, todo lo que debemos hacer es buscar todos los vértices factibles y luego evaluar la función objetivo en dichos vértices para encontrar el punto óptimo.
En el caso de programas no lineales, el problema es mucho más difícil de resolver porque la solución podría estar en cualquier parte dentro de la región factible, en el límite de la región factible o en un vértice.
Por suerte, la mayoría de los problemas de optimización empresarial son lineales y es por eso que la PL es tan popular. Hoy en día, existen más de 400 paquetes de software en el mercado para resolver problemas de PL. La mayoría se basa en la búsqueda de vértices. Esto equivale a pasar de un vértice a otro cercano en busca de un punto óptimo.
Vínculo entre Programación Lineal y Sistemas de Ecuaciones
George Dantzig la programación lineal es estrictamente "la teoría y la solución de sistemas lineales de desigualdad". Probablemente ya ha notado que las soluciones básicas de un programa lineal son las soluciones de los sistemas de ecuaciones que constan de restricciones en una posición obligatoria.Por ejemplo, en el caso del Problema del Carpintero, se pueden calcular todas las soluciones básicas, tomando dos ecuaciones cualquiera y resolviéndolas al mismo tiempo. Luego, se utilizan las restricciones de las otras ecuaciones para verificar la factibilidad de esta solución. Si es factible, esta solución es una solución básica factible que proporciona las coordenadas de un punto extremo de la región factible. Para ilustrar el procedimiento, considere las restricciones del Carpintero en la posición obligatoria (es decir todas con signo =):
2X1 + X2 = 40
X1 + 2X2 = 50
X1 = 0
X2 = 0
Aquí tenemos 4 ecuaciones con 2 incógnitas. Existen como máximo C42 = 4! / (2! 2!) = 6 soluciones básicas. Si resolvemos los seis sistemas de ecuaciones resultantes tenemos:
| X1 | X2 | 5X1 + 3X2 | |
| 10 | 20 | 110* | |
| 0 | 40 | No factible | |
| 20 | 0 | 100 | |
| 0 | 25 | 75 | |
| 50 | 0 | No factible | |
| 0 | 0 | 0 |
Cuatro de las soluciones básicas que figuran arriba son soluciones básicas factibles que satisfacen todas las restricciones y pertenecen a los vértices de la región factible. Al incluir la solución básica factible en la función objetivo, podemos calcular el valor óptimo. Entonces, de la tabla anterior surge que la solución óptima es X1 = 10, X2 = 20, con un valor óptimo de US$110. Este abordaje puede aplicarse para resolver problemas de PL de más dimensiones.
Extensión a Mayores Dimensiones
El Método Gráfico se limita a resolver problemas de PL con una o dos variables de decisión. Sin embargo, proporciona una clara ilustración de dónde se encuentran las regiones factibles y no factibles así como también los vértices. Desarrollar una comprensión visual del problema contribuye a un proceso de pensamiento más racional. Por ejemplo, ya vimos que: si un programa lineal tiene una región factible acotada no vacía, la solución óptima es siempre uno de los vértices de su región factible (una esquina o punto extremo). Como resultado, lo que debemos hacer es buscar todos los puntos de intersección (vértices) y luego examinar cuál de todos los vértices factibles proporciona la solución óptima. Ahora, aplicando conceptos de Geometría Analítica, sortearemos esta limitación de la visión humana. El Método Algebraico está diseñado para extender los resultados del método gráfico a problemas de PL multidimensionales, tal como se ilustra en el siguiente ejemplo numérico.Ejemplo Numérico: el Problema del Transporte
El objetivo es encontrar la manera más efectiva de transportar productos. La siguiente tabla presenta un resumen de la oferta y la demanda en cada origen (por ejemplo: el depósito) O1, O2 y destino (por ejemplo: el mercado) D1 y D2, junto con el costo unitario de transporte.| Matriz de Costo Unitario de Transporte | ||||
| D1 | D2 | Oferta | ||
| O1 | 20 | 30 | 200 | |
| O2 | 10 | 40 | 100 | |
| Demanda | 150 | 150 | 300 | |
Xij representa la cantidad de productos enviados desde el origen i hasta el destino j. La formulación de PL del problema de minimización del costo total de transporte es la siguiente:
Min 20X11 + 30X12 + 10X21 + 40X22
Sujeta a:
X11 + X12 = 200
X21 + X22 = 100
X11 + X21 = 150
X12 + X22 = 150
todas Xij ³ 0
Como este problema de transporte es equilibrado (oferta total = demanda total) todas las restricciones están en forma de igualdad. Además, cualquiera de las restricciones es redundante (si se suman dos restricciones cualquiera y se resta otra obtenemos la restricción restante). Borremos la última restricción. El problema entonces queda así:
Min 20X11 + 30X12 + 10X21 + 40X22
Sujeta a:
X11 + X12 = 200
X21 + X22 = 100
X11 + X21 = 150
todas Xij ³ 0
Este problema de PL no se puede resolver mediante el método gráfico. Sin embargo, el método algebraico no tiene ninguna limitación con respecto a la dimensión de PL. Nótese que tenemos tres ecuaciones con cuatro variables de decisión restringidas. Fijando cualquiera de las variables en cero obtenemos:
| X11 | X12 | X21 | X22 | Costo Total de Transporte |
| 0 | 200 | 150 | -50 | No factible |
| 200 | 0 | -50 | 150 | No factible |
| 150 | 50 | 0 | 100 | 8500 |
| 50 | 150 | 100 | 0 | 6500* |
Ahora poniendo cualquier y dos (o más) las variables para poner cero de a, es fácil de ver, inspeccionando las tres ecuaciones que todas las otras soluciones son no factible.
Por lo tanto, la estrategia óptima es X11 = 50, X12 = 150, X21 = 100, y X22 = 0, con un costo total de transporte mínimo de US$6.500.
Si lo desea, puede resolver este problema con Modul Net.Exe en el paquete WinQSB para verificar estos resultados.
Para obtener una versión más detallada del Método Algebraico, visite el sitio Toward the Simplex Method
Conceptos y Técnicas de Aprendizaje Asistidos por Computadora
Debemos ser precavidos al cuestionar nuestra intuición y demostrar porqué debemos aprender mediante un instrumento que en este curso es un paquete de software. Todos los alumnos de Física y Química realizan experimentos en los laboratorios para conocer bien los temas de estos dos campos de estudio. Usted también debe realizar experimentos para comprender los conceptos de la Ciencia de Administración. Por ejemplo, debe utilizar paquetes de software para realizar análisis what-if o de hipótesis. El software le permite observar los efectos de la variación de los valores dados.Los programas lineales reales siempre se resuelven por computadora. Por lo general las computadoras utilizan el método simplex para llegar a las soluciones. Los coeficientes de la función objetivo se denominan coeficientes de costos (porque históricamente durante la Segunda Guerra Mundial, el primer problema de PL fue un problema de minimización de costos), coeficientes tecnológicos y valores RHS (o valores del lado derecho). Esta es la manera perfecta de aprender conceptos del análisis de sensibilidad. Como usuario, usted puede darse el lujo de ver resultados numéricos y compararlos con lo que usted espera ver.
El paquete LINDO es un software muy utilizado para problemas de PL. Se puede bajar una versión para Windows gratuita en la página Home de LINDO en LINDO, http://www.lindo.com. En este sitio se explica como ejecutar e interpretar los resultados del paquete LINDO.
¡Precaución! Antes de utilizar cualquier software, verifique que sea confiable.
Aquí encontrará una Guía de Software de PL para su revisión: LP Software Guide.
Cómo Interpretar los Resultados del Paquete de Software LINDO
En este curso, utilizamos paquetes de software con dos objetivos distintos. Queremos realizar muchos experimentos numéricos utilizando paquetes de software como herramientas para resolver muchos problemas a fin de ver por nosotros mismos, y comprender todos los conceptos teóricos (como por ejemplo, los precios sombra) contenidos en los temas del curso. Esto comprende también las herramientas de computación disponibles en la Web. Por último, aprendemos a usar e interpretar los resultados de los paquetes de software a fin de resolver problemas prácticos de gran tamaño.
Lindo es un paquete de software muy popular que resuelve problemas lineales. La aplicación LP/ILP de WinQSB realiza las mismas operaciones que Lindo pero de una manera mucho más fácil de usar.
El nombre LINDO es la abreviatura en inglés de Linear INteractive Discrete Optimization (Optimización Lineal Discreta e INteractiva). Aquí la palabra "discreta" significa pasar de una solución factible básica a la siguiente en lugar de desplazarse por toda la región factible en busca de la solución básica factible óptima (si la hubiere).
Al igual que todos los paquetes de PL, tal como WinQSB, Lindo emplea el método simplex. Junto con la solución del problema, el programa también proporciona un análisis común de sensibilidad de los Coeficientes de la Función Objetivo (denominados Coeficientes de Costos) y el RHS de las restricciones. A continuación, presentamos una explicación de los resultados del paquete LINDO.
Supóngase que usted desea correr el Problema del Carpintero. Inicie el paquete LINDO (o WinQSB). Desde el teclado escriba lo siguiente en la venta actual:
MAX 5X1 + 3X2
S.T. 2X1 + X2 < 40
X1 + 2X2 < 50
End
{MAX 5X1 + 3X2, Sujeta a 2X1 + X2 < 40 X1 + 2X2 < 50, Fin }
- La función objetivo no debería contener ninguna restricción. Por ejemplo, no se puede ingresar Max 2X1 + 5.
- Todas las variables deben aparecer en el lado izquierdo de las restricciones, mientras que los valores numéricos deben aparecer en el lado derecho de las restricciones (es por eso que a estos números se los denomina valores RHS o valores del lado derecho).
- Se presupone que todas las variables son no negativas. No ingrese las condiciones de no negatividad.
Si desea obtener todas Tablas Simplex, entonces
- Haga clic en "Reports" (Informes) y luego elija "Tableau" (Tabla), luego haga clic en "Solve" (Resolver) y elija "Pivot" haga clic en "OK" (Aceptar), "Close" (Cerrar), "Cancel" (Cancelar), continúe de esta manera hasta que aparezca el mensaje "Do? Range (Sensitivity) Analysis" (Desea realizar un análisis de rango [de sensibilidad]?). Seleccione "Yes" (Sí), si lo desea. Después de minimizar la ventana actual, verá el resultado que puede imprimir para su análisis gerencial.
- De lo contrario, haga clic en "Solve" (Resolver), y luego elija "Solve" (Resolver).
En la parte superior de la página aparece la tabla inicial y a lo largo de la parte superior de la tabla figuran las variables. La primera fila de la tabla es la función objetivo. La segunda fila es la primera restricción. La tercera fila es la segunda restricción y así sucesivamente hasta enumerar todas las restricciones en la tabla.
Después de la tabla inicial aparece un enunciado que indica la variable de entrada y la variable de salida. La variable de salida está expresada como la fila donde se colocará la variable de entrada. Luego se imprime la primera tabla de iteraciones. Se sigue ingresando sentencias y continúan las iteraciones de la tabla continúan hasta llegar a la solución óptima.
La siguiente sentencia, `LP OPTIMUM FOUND AT STEP 2' (OPTIMO DE PL ENCONTRADO EN EL PASO 2) indica que se encontró la solución óptima en la iteración 2 de la tabla inicial. Inmediatamente debajo aparece el óptimo del valor de la función objetivo. Este es el dato más importante que le interesa a todo gerente.
Muchas veces, aparecerá un mensaje que lo sorprenderá: "LP OPTIMUM FOUND AT STEP 0" (OPTIMO DE PL ENCONTRADO EN EL PASO 0). ¿Cómo puede ser paso 0? ¿No es necesario primero desplazarse para encontrar un resultado...? Este mensaje es muy confuso. Lindo lleva un registro en su memoria de todas la actividades previas realizadas antes de resolver cualquier problema que usted ingrese. Por lo tanto, no muestra exactamente cuántas iteraciones fueron necesarias para resolver el problema en cuestión. A continuación presentamos una explicación detallada y una solución para saber con exactitud la cantidad de iteraciones: Supóngase que usted corre el problema más de una vez o resuelve un problema similar. Para saber cuántas iteraciones lleva realmente resolver un problema en particular, debe salir de Lindo y luego reingresar, volver a escribir y a presentar el problema. De esta manera aparecerá la cantidad exacta de vértices (excluyendo el origen) visitados para llegar a la solución óptima (si es que existe) en forma correcta.
Después de esto sigue la solución del problema, es decir la estrategia para fijar las variables de decisión a fin de lograr el valor óptimo antes mencionado. Esto aparece con una columna de variables y una columna de valores. La columna de valores contiene la solución del problema. La reducción de costos asociada con cada variable se imprime a la derecha de la columna de valores. Estos valores se toman directamente de la tabla simplex final. La columna de valores proviene del RHS. La columna de reducción de costos proviene directamente de la fila indicadora.
Debajo de la solución, aparecen los valores de las variables de holgura / excedente de la tabla final. Los valores de las variables de holgura / excedente para la solución final figuran en la columna `SLACK OR SURPLUS' (HOLGURA O EXCEDENTE). Los precios sombra relacionados aparecen a la derecha. Recuerde: Holgura representa la cantidad que sobra de un recurso y Excedente representa el exceso de producción.
La restricción obligatoria se puede encontrar buscando la variable de holgura / excedente con el valor de cero. Luego, examine cada restricción para encontrar la que tenga sólo esta variable especificada. Otra manera de expresar esto es buscar la restricción que exprese igualdad en la solución final.
Debajo, aparece el análisis de sensibilidad de los coeficientes de costos (es decir de los coeficientes de la función objetivo). Cada parámetro de coeficiente de costos puede variar sin afectar la solución óptima actual. El valor actual del coeficiente se imprime junto con los valores de límite superior e inferior permitidos para que la solución siga siendo óptima.
Debajo aparece el análisis de sensibilidad para el RHS. La columna de "filas" imprime el número de fila del problema inicial. Pro ejemplo, la primera fila impresa será la dos porque la fila uno es la función objetivo. La primera restricción es la fila dos. El RHS de la primera restricción está representado por la fila dos. A la derecha, aparecen los valores para los cuales el valor RHS puede cambiar manteniendo la validez de los precios sombra.
Nótese que en la tabla simplex final, los coeficientes de las variables de holgura / excedente en la fila objetivo proporcionan la unidad del valor del recurso. Estos números se denominan precios sombra o precios duales. Debemos tener cuidado al aplicar estos números. Sólo sirven para pequeños cambios en las cantidades de recursos (es decir, dentro de los rangos de sensibilidad del RHS).
Cómo crear condiciones de no negatividad (variables libres): Por omisión, prácticamente todos los paquetes de software de resolución de problemas de PL (como por ejemplo LINDO) presuponen que todas las variables son no negativas.
Para cumplir con este requerimiento, convierta cualquier variable no restringida Xj en dos variables no negativas reemplazando cada Xj por y - Xj. Esto aumenta la dimensionalidad del problema sólo en uno (introducir una variable y) independientemente de cuántas variables sean no restringidas.
Si cualquier variable Xj está restringida a ser no positiva, reemplace cada Xj por - Xj. Esto reduce la complejidad del problema.
Resuelva el problema convertido y luego vuelva a ingresar los valores de las variables originales.
Ejemplos Numéricos
Maximizar -X1
sujeta a:
X1 + X2 ³ 0,
X1 + 3X2 £ 3.
El problema convertido es:
Maximizar -y + X1
sujeta a:
-X1 - X2 + 2y ³ 0,
-X1 - 3X2 + 4y £ 3,
X1 ³ 0,
X2 ³ 0,
and y ³ 0.
La solución óptima para las variables originales es: X1 = 3/2 - 3 = -3/2, X2 = 3/2 - 0 = 3/2, con valor óptimo de 3/2.
Para detalles acerca de los algoritmos de solución, visite el sitio Web Artificial-Free Solution Algorithms, ejemplo N° 7.
Implementaciones de Computación con el Paquete WinQSB
Utilice el módulo LP/ILP de su paquete WinQSB para cumplir dos objetivos: resolver grandes problemas y realizar experimentos numéricos para comprender los conceptos presentados en las secciones LP y ILP.Tipo de variable: seleccione el tipo de variable desde la pantalla "Problem Specification" (Especificación del Problema) (la primera pantalla que aparece al ingresar un nuevo problema); para programación lineal, utilice la opción predeterminada "Continuous" (Continua).
Formato de datos de entrada: seleccione el formato de datos de entrada desde la pantalla "Problem Specification" (Especificación del Problema). Normalmente, es preferible utilizar el formato Matrix (Matriz) para ingresar los datos. En el formato Normal, el modelo aparece ya ingresado. Este formato puede ser más conveniente cuando se debe resolver un problema grande con muchas variables. Puede desplazarse por los formatos seleccionando el botón "Switch to the…" (Cambiar a ...) del menú Format (Formato).
Identificación de Variables / Restricciones: es conveniente cambiar los nombres de las variables y las restricciones para facilitar la identificación del contexto que representan. Los nombres de las variables y las restricciones se pueden cambiar desde el menú Edit (Edición).
Autoajuste de ancho de columnas (Best Fit): Con el botón "best fit" del menú Format (Formato) cada columna puede tener su propio ancho.
Resolver buscando la solución óptima (si es que existe): Seleccione "Solve the problem" (Resolver el problema) desde el menú "Solve and Analyze" (Resolver y Analizar), o utilice el ícono "Solve" (Resolver) que se encuentra en la parte superior de la pantalla. Esto genera un "Combined Report" (Informe Combinado) que brinda la solución y los resultados adicionales (reducción de costos, rangos de optimalidad, holgura / excedente, rango de factibilidad y precios sombra).
Resolver mediante el Método Gráfico: seleccione el método gráfico desde el menú "Solve and Analyze" (Resolver y Analizar) (sólo se puede utilizar para problemas de dos variables). También puede hacer clic en el ícono Graph (Gráfico) en la parte superior de la pantalla. Puede ajustar los rangos X-Y después de resolver el problema y de que aparezca el gráfico. Elija el menú Option (Opción) y seleccione los nuevos rangos desde la lista desplegable.
Soluciones Optimas Alternas (si es que existen): después de resolver el problema, si aparece un mensaje que le informa: "Alternate solution exists!!" (¡¡Existe una solución alterna!!), para ver todas las soluciones óptimas de los puntos extremos elija el menú Results (Resultados) y luego seleccione "Obtain alternate optimal" (Obtener óptimo alterno). Visite también la sección Soluciones Múltiples de este sitio Web para ver algunas advertencias.
Notas:
Utilice el archivo de Ayuda ("Help") del paquete WinQSB para aprender cómo funciona.
Para ingresar problemas en el software QSB; para una restricción tal como X1 + X2 ³ 50, el coeficiente es 1 y debe ingresarse de esta manera en el software. Para cualquier variable que no se utilice en esa restricción en particular (por ejemplo si el problema tuviera X3 pero no fuera parte de la restricción mencionada) simplemente deje la celda en blanco para esa restricción.
Puede cambiar la dirección de una restricción haciendo clic en la celda.
Para construir el dual de un determinado problema, haga clic en Format (Formato), luego seleccione "Switch to the Dual Form" (Cambiar a la forma dual).
¿Cómo Resolver un Sistema de Ecuaciones Lineales Utilizando un Software de PL?
Ya dijimos que en el Método Algebraico de resolución de problemas de PL, debemos resolver algunos sistemas de ecuaciones. Por consiguiente, existe un vínculo entre los paquetes de software para resolver problemas de PL y aquellos que sirven para resolver sistemas de ecuaciones. Supóngase que tenemos un sistema de ecuaciones muy grande que queremos resolver y tenemos un paquete de software de resolución de problemas de PL pero no tenemos ningún paquete de resolución de sistemas de ecuaciones. La pregunta es "¿Cómo se puede utilizar un paquete de software de PL para encontrar la solución de un sistema de ecuaciones?" Los siguientes pasos esbozan el proceso de resolución de cualquier sistema de ecuaciones lineales mediante un paquete de resolución de problemas de PL.
1- Debido a que los paquetes de resolución de problemas de PL requieren que todas las variables sean no negativas, por cada variable substituya Xi = Yi - T en todas partes.
2- Cree un objetivo artificial, como por ejemplo minimizar T
3- Las restricciones del problema de PL son las ecuaciones del sistema después de las sustituciones mencionadas en el paso 1.
Ejemplo numérico: resolver el siguiente sistema de ecuaciones
2X1 + X2 = 3
X1 -X2 = 3
Dado que el paquete WinQSB acepta PL en diversos formatos (a diferencia de LINDO), la resolución del problema utilizando WinQSB es sencilla:
Primero, cree una PL con un objetivo artificial como por ejemplo Max X1, sujeta a 2X1 + X2 = 3, X1 - X2 = 3, y tanto X1 como X2 sin restricción de signo. Luego, ingrese esta PL en el módulo LP/ILP para arribar a la solución.
Si usted utiliza un paquete de software de PL que requiere que todas las variables sean no negativas, primero substituya X1 = Y1 - T y X2 = Y2 - T en ambas ecuaciones. También necesitamos una función objetivo. Fijemos una función objetivo artificial como por ejemplo minimizar T. El resultado es la siguiente PL:
Min T
Sujeta a:
2Y1 + Y2 - 3T = 3,
Y1 - Y2 = 3.
Utilizando cualquier software de PL, como Lindo o WinQSB, llegamos a la solución óptima Y1 = 3, Y2 = 0, T = 1. Ahora, sustituya esta solución de PL en ambas transformaciones X1 = Y1 - T y X2 = Y2 - T. Esto nos da los valores numéricos para nuestras variables originales. Por ende, la solución del sistema de ecuaciones es X1 = 3 - 1 = 2, X2 = 0 - 1 = -1, la cual se puede verificar fácilmente.
Problema Dual: Construcción y Significado
Asociado a cada problema (primario) de PL existe un problema correspondiente denominado problema dual. La siguiente clasificación de las restricciones de las variables de decisión resulta útil y fácil de recordar para construir el problema dual.
|
|
|||||||||||
|
Construcción de Problemas Duales:
- Si el problema primario es un problema de maximización, entonces su problema dual es un problema de minimización (y viceversa).
- Utilice el tipo de variable de un problema para determinar el tipo de restricción del otro problema.
- Utilice el tipo de restricción de un problema para determinar el tipo de variable del otro problema.
-Los elementos RHS de un problema se transforman en los coeficientes de la función objetivo del otro problema (y viceversa).
- Los coeficientes de la matriz de las restricciones de un problema son la transposición de los coeficientes de la matriz de las restricciones del otro problema.
Puede verificar las reglas de construcción del problema dual utilizando su paquete WinQSB.
Ejemplos Numéricos:
Considere el siguiente problema primario:
min x1 - 2x2
sujeta a:
x1 + x2 ³ 2,
x1 - x2 £ -1,
x2 ³ 3,
x1, x2 ³ 0.
Siguiendo la regla de construcción antes mencionada, el problema dual es:
max 2u1 - u2 + 3u3
sujeta a:
u1 + u2 £ 1,
u1 - u2 + u3 £ -2,
u1 ³ 0,
u2 £ 0,
u3 ³ 0
El Problema Dual del Problema del Carpintero:
Maximizar 5X1 + 3X2
sujeta a:
2X1 + X2 £ 40
X1 + 2X2 £ 50
X1 ³ 0
X2 ³ 0
El problema dual es:
Minimizar 40U1 + 50U2
Sujeta a:
2U1 + U2 ³ 5
U1 + 2U2 ³ 3
U1 ³ 0
U2 ³ 0
Aplicaciones: usted puede utilizar la dualidad en una amplia gama de aplicaciones tales como:
- En algunos casos, puede ser más eficiente resolver el problema dual que el primario.
- La solución dual proporciona una interpretación económica importante tal como los precios sombra (es decir, los valores marginales de los elementos RHS) que son los multiplicadores Lagrangianos que demuestran una cota (estricta) del valor óptimo del problema primario y viceversa. Históricamente, el precio sombra se definió como la mejora en el valor de la función objetivo por aumento unitario en el lado derecho, porque el problema generalmente adoptaba la forma de una mejora de maximización de utilidades (es decir, un aumento). El precio sombra puede no ser el precio de mercado. El precio sombra es por ejemplo el valor del recurso bajo la "sombra" de la actividad comercial. Se puede realizar un análisis de sensibilidad,es decir un análisis del efecto de pequeñas variaciones en los parámetros del sistema sobre las medidas de producción, calculando las derivadas de las medidas de producción con respecto al parámetro.
- Si una restricción en un problema no es obligatoria (en otras palabras, el valor LHS o valor del lado izquierdo) concuerda con el valor RHS), la variable asociada en el problema es cero. De manera inversa, si una variable de decisión en un problema no es cero, la restricción asociada en el otro problema es obligatoria. A estos resultados se los conoce como Condiciones Complementarias de Holgura.
- Obtener el rango de sensibilidad del RHS de un problema partiendo del rango de sensibilidad del coeficiente de costos del otro problema y viceversa.
Para más detalles y ejemplos numéricos, lea los siguientes artículos:
A. Benjamin, Sensible Rules for Remembering Duals_ S-O-B Method, SIAM Review, 37, 85-87, 1995.
H. Arsham, An Artificial-Free Simplex Algorithm for General LP Models, Mathematical and Computer Modelling, 25, 107-123, 1997.
El Problema Dual del Problema del Carpintero y su Interpretación
En esta sección, construiremos el Problema Dual del Problema del Carpintero y presentaremos la interpretación económica del mismo.Recordemos los parámetros de entrada no controlables del Problema del Carpintero:
| Datos de entrada no controlables | ||||
| Mesas | Sillas | Disponible | ||
| Mano de obra | 2 | 1 | 40 | |
| Materia prima | 1 | 2 | 50 | |
| Ingresos netos | 5 | 3 | ||
Y su formulación de PL
Maximizar 5 X1 + 3 X2
Sujeta a:
2 X1 + X2 £ 40 restricción de mano de obra
X1 + 2 X2 £ 50 restricción de materiales
tanto X1 como X2 son no negativas.
Donde X1 y X2 representan la cantidad de mesas y sillas a fabricar.
Supóngase que el Carpintero desea contratar un seguro para sus ingresos netos. Digamos que:
U1 = el monto en dólares pagadero al Carpintero por cada hora de trabajo perdida (por enfermedad, por ejemplo),
U2 = el monto en dólares pagadero al Carpintero por cada unidad de materia prima perdida (por incendio, por ejemplo).
Por supuesto que el corredor de seguros intenta minimizar el monto total de US$(40U1 + 50U2) pagadero al Carpintero por la Compañía de Seguros. Sin embargo, como es de esperar, el Carpintero fijará las restricciones (es decir las condiciones) para que la compañía de seguros cubra toda su pérdida que equivale a sus ingresos netos debido a que no puede fabricar los productos. En consecuencia, el problema de la compañía de seguros es:
Minimizar 40 U1 + 50 U2
Sujeta a:
2U1 + 1U2 ³ 5 ingresos netos por una mesa
1U1 + 2U2 ³ 3 ingresos netos por una silla
U1, U2 son no negativas.
Si implementa este problema en un paquete de software, verá que la solución óptima es U1 = US$7/3 y U2 = US$1/3 con el valor óptimo de US$110 (el monto que el Carpintero espera recibir). Esto asegura que el Carpintero pueda manejar su vida sin inconvenientes. El único costo es la prima que le cobra la compañía de seguros.
Como puede ver, el problema de la compañía de seguros está estrechamente relacionado con el problema original.
Según la terminología del proceso de diseño de modelos de IO/CA, el problema original se denomina Problema Primario mientras que el problema relacionado se denomina Problema Dual
Tal como vimos en el Problema del Carpintero y su Problema Dual, el Valor Optimo es siempre el mismo para ambos problemas. Esto se denomina Equilibrio Económico entre el Problema Primario y el Problema Dual.
Errores de Redondeo cometido por los Gerentes: tenga cuidado siempre que redondee el valor de los precios sombra. Por ejemplo, el precio sombra de la restricción de recursos en el problema anterior es 8/3, por ende, si usted desea comprar más de este recurso, no debería pagar más de US$2.66. Sin embargo, siempre que usted quiera vender cualquier unidad de este recurso, no debería hacerlo a un precio inferior a US$2.67.
Podría darse un error similar si usted redondea en los límites de los rangos de sensibilidad. Como siempre, hay que prestar atención porque el límite superior e inferior deben redondearse para abajo y para arriba, respectivamente.
Cálculo de los Precios Sombra
Ahora ya sabe que los precios sombra son la solución del problema dual. Aquí tenemos un ejemplo numérico.Calcule el precio sombra para ambos recursos en el siguiente problema de PL:
Max -X1 + 2X2
sujeta a:
X1 + X2 £ 5
X1 + 2X2 £ 6
tanto X1 como X2 son no negativas.
La solución de este problema primario (utilizando por ejemplo el método gráfico) es X1 = 0, X2 = 3, con el sobrante S1 = 2 del primer recurso mientras que el segundo recurso se utiliza por completo, S2 = 0.
Los precios sombra son la solución del problema dual:
Min 5U1 + 6U2
Sujeta a:
U1 + U2 ³ -1
U1 + 2U2 ³ 2
tanto U1 como U2 son no negativas.
La solución del problema dual (utilizando por ejemplo el método gráfico) es U1 = 0, U2 = 1 que son los precios sombra para el primer y el segundo recurso, respectivamente. Fíjese que siempre que la holgura / excedente de una restricción no es cero, el precio sombra relacionado con ese RHS de la restricción es siempre cero, pero puede no darse el caso contrario. En este ejemplo numérico S1 = 2 (es decir, el valor de holgura del RHS 1 del problema primario), que no es cero; por lo tanto U1 es igual a cero tal como es de esperar.
Considere el siguiente problema:
Max X1 + X2
sujeta a:
X1 £ 1
X2 £ 1
X1 + X2 £ 2
todas las variables de decisión ³ 0.
Utilizando un paquete de software, puede verificar que el precio sombra para el tercer recurso es cero, mientras que no hay sobrante de ese recurso en la solución óptima X1 =1, X2 = 1.
Comportamiento de los Cambios en los Valores RHS del Valor Optimo
Para estudiar los cambios direccionales en el valor óptimo con respecto a los cambios en el RHS (sin restricciones redundantes y con todos los RHS ³0) distinguimos los dos casos presentados a continuación:Caso I: Problema de Maximización
Para restricción de £ : cambio en la misma dirección. Vale decir que un aumento en el valor RHS no produce una disminución en el valor óptimo sino que éste aumenta o permanece igual según la restricción sea obligatoria o no obligatoria.
Para restricción de ³ : cambio en la dirección opuesta. Vale decir que un aumento en el valor RHS no produce un aumento en el valor óptimo sino que éste disminuye o permanece igual según la restricción sea obligatoria o no obligatoria.
Para restricción de =: el cambio puede ser en cualquier dirección (ver la sección Más por Menos en este sitio).
Caso II: Problema de Minimización
Para restricción de £ : cambio en la dirección opuesta. Vale decir que un aumento en el valor RHS no produce un aumento del valor óptimo sino que éste disminuye o permanece igual según la restricción sea obligatoria o no obligatoria).
Para restricción de ³ : cambio en la misma dirección. Vale decir que un aumento en el valor RHS no produce una disminución del valor óptimo sino que éste aumenta o permanece igual según la restricción sea obligatoria o no obligatoria.
Para restricción de =: el cambio puede ser en cualquier dirección (ver la sección Más por Menos en este sitio).
Interpretación Incorrecta del Precio Sombra
El Precio Sombra nos indica cuánto cambiará la función objetivo si cambiamos el lado derecho de la correspondiente restricción. Esto normalmente se denomina "valor marginal", "precios duales" o "valor dual" para la restricción. Por lo tanto, el precio sombra puede no coincidir con el "precio de mercado".Por cada restricción del RHS, el Precio Sombra nos indica exactamente cuánto cambiará la función objetivo si cambiamos el lado derecho de la restricción correspondiente dentro de los límites fijados por el rango de sensibilidad del RHS.
Por consiguiente, por cada valor RHS, el precio sombra es el coeficiente del cambio en el valor óptimo causado por cualquier aumento o disminución admisible en el RHS dentro del cambio admisible.
Dado que el cambio en el RHS está dentro del rango de sensibilidad.
Un anti-ejemplo:
Considere la siguiente PL:
Max X2
sujeta a:
X1 + X2 £ 2
2.5X1 + 4X2 £ 10
Donde ambas variables de decisión son no negativas.
El problema tiene su solución óptima en (0, 2) con un valor óptimo de 2.
Supóngase que quiere calcular el precio sombra del primer recurso, es decir el RHS de la primera restricción.
Si cambiamos el RHS de la primera restricción aumentándolo en una unidad tenemos:
Max X2
sujeta a:
X1 + X2 £ 3
2.5X1 + 4X2 £ 10
donde ambas variables de decisión son no negativas.
El nuevo problema tiene la solución óptima (0, 2.5) con un valor óptimo de 2.5.
Entonces, pareciera "como si" el precio sombra de este recurso es 2.5 - 2 = 0.5. De hecho, el precio sombra de este recurso es 1, el cual se puede verificar construyendo y resolviendo el problema dual.
El motivo de este error se torna obvio si observamos que el aumento admisible para mantener la validez del precio sombra del primer recurso es 0.5. El aumento en 1 excede el cambio admisible del primer valor RHS.
Ahora supóngase que cambiamos el mismo valor RHS en + 0.1 que es admisible. Entonces el valor óptimo del nuevo problema es 2.1. Por consiguiente, el precio sombra es (2.1 -2) / 0.1 = 1. Es necesario prestar mucha atención al calcular los precios sombra.
Si usted quiere calcular el precio sombra de un valor RHS sin tener su rango de sensibilidad, puede obtener los valores óptimos de dos perturbaciones como mínimo. Si el índice de cambio en ambos casos arroja los mismos valores, entonces este índice es realmente el precio sombra. A modo de ejemplo, supóngase que perturbamos el RHS de la primera restricción en +0.02 y -0.01. Si resolvemos el problema después de estos cambios utilizando un software de PL, obtenemos los valores óptimos de 2.02 y 1.09, respectivamente. Como el valor óptimo para el problema nominal (sin ninguna perturbación) es igual a 2, el índice de cambio para los dos casos es: (2.02 - 2)/0.02 = 1, y (1.09 - 2)/(-0.01) = 1, respectivamente. Como estos dos índices coinciden, podemos concluir que el precio sombra del RHS de la primera restricción es de hecho igual a 1.
¿El Precio Sombra es Siempre No Negativo?
Probablemente se esté preguntando si el precio sombra de un valor RHS es siempre no negativo. Todo depende de la formulación del problema primario y de su correspondiente dual. Lo importante es recordar que el precio sombra de un determinado valor RHS es el índice de cambio del valor óptimo con respecto al cambio en ese RHS, dado que el cambio se encuentra dentro de los límites de ese RHS.Considere el siguiente ejemplo numérico:
Max 3X1 + 5X2
Sujeta a:
X1 + 2X2 £ 50
-X1 + X2 ³ 10
X1, X2 son no negativas.
Nos interesa saber el precio sombra del valor del RHS 2 = 10. El problema dual es:
Min 50U1 + 10U2
Sujeta a:
U1 - U2 ³ 3
2U1 + U2 £ 5
U1 ³ 0, mientras que U2 £ 0
Esto se puede verificar con el software WinQSB. La solución del problema dual es U1 = 8/3, U2 = -1/3. Por lo tanto, el precio sombra del valor RHS 2 = 10 es U2 = -1/3. Es decir que por cada aumento (disminución) unitario en el RHS2, el valor óptimo del problema primario disminuye (aumenta) en 1/3, dado que el cambio en RHS 2 está dentro de los límites de sensibilidad.
Para otra versión del mismo problema primario, fíjese que el problema puede escribirse de la misma manera, cambiando la dirección de la segunda restricción de desigualdad:
Max 3X1 + 5X2
Sujeta a:
X1 + 2X2 £ 50
X1 - X2 £ -10
X1, X2 son no negativas.
El problema dual de este problema primario ahora es:
Min 50Y1 - 10Y2
Sujeta a:
Y1 + Y2 ³ 3
2Y1- Y2 £ 5
tanto Y1 como Y2 son no negativas
Nuevamente, la formulación dual puede verificarse utilizando el software WinQSB. La solución de este problema dual es Y1 = 8/3 y Y2 = 1/3. Entonces, el precio sombra del valor del RHS 2 = -10 es Y2 = 1/3. Vale decir que por cada aumento (disminución) unitario en el valor RHS 2, el valor óptimo del problema primario aumenta (disminuye) en 1/3, dado que el cambio en RHS 2 esta dentro de los límites de sensibilidad.
Como ya debe haber notado, ambos problemas duales son iguales al sustituir U1 = Y1, y U2 = -Y2. Esto significa que los precios sombra obtenido para RHS 2 = 10, y RHS 2 = -10 tienen el mismo valor con el signo opuesto (como es de esperar). Por ende, , el signo del precio sombra depende de cómo se formule el problema dual , aunque el significado y su interpretación son siempre los mismos.
Precios Sombra Alternativos
Supóngase que tenemos una PL que tiene una única solución óptima. ¿Es posible tener más de un conjunto de precios duales?Sí, es posible. Considere el siguiente problema:
Min 16X1 + 24X2
sujeta a:
X1 + 3X2 ³ 6
2X1 + 2X2 ³ 4
todas las variables de decisión ³ 0.
Su dual es:
Max 6U1 + 4U2
sujeta a:
U1 + 2U2 £ 16
3U1 + 2U2 £ 24
todas las variables de decisión ³ 0,
Este problema dual tiene diversas soluciones alternativas, tales como, (U1 = 8, U2 = 0) y (U1 = 4, U2 = 6). Todas las combinaciones convexas de estos dos vértices también son soluciones.
Existen casos generales para los cuales los precios sombra no son únicos. Como en el ejemplo anterior, siempre que exista redundancia entre las restricciones, o si la solución óptima es "degenerada", puede haber más de un conjunto de precios duales. En general, las restricciones lineales independientes son condición suficiente para que exista un único precio sombra.
Considere el siguiente problema de PL con una restricción redundante:
Max 10X1 + 13X2
sujeta a:
X1 + X2 = 1
X1 + X2 = 1
X1+2X2 = 2
y todas las variables son no negativas.
Si corremos el problema dual en Lindo vemos que X1 = 0, X2 = 1, con precios sombra (0, 13, 0).
Si utilizamos WinQSB para este problema, obtenemos X1 = 0, X2 = 1 con distintos precios sombra (0, 7, 3).
En el caso de redundancia, los precios sombra obtenidos con un paquete de PL pueden no coincidir con aquellos obtenidos con otro paquete de software.
Manejo de Incertidumbres mediante Modelación de Escenarios:
Análisis de Sensibilidad y Análisis de Especificidad
El entorno comercial muchas veces es impredecible e incierto debido a factores tales como cambios económicos, reglamentaciones públicas, dependencia de subcontratistas y proveedores, etc. Los gerentes generalmente se ven inmersos en un entorno dinámico e inestable donde aun los planes a corto plazo deben re-evaluarse constantemente y ajustarse de manera incremental. Todo esto requiere una mentalidad orientada al cambio para hacer frente a las incertidumbres. Recuerde que las sorpresas no forman parte de una decisión sólida.
Análisis de Sensibilidad y Análisis de Especificidad
El hombre utiliza construcciones (modelos) matemáticas e informáticas para una variedad de entornos y propósitos, con frecuencia para conocer los posibles resultados de uno o más planes de acción. Esto puede relacionarse con inversiones financieras, alternativas de seguros (asegurar o no asegurar/cuánto), prácticas industriales e impactos ambientales. El uso de modelos se ve perjudicado por la inevitable presencia de incertidumbres, que surgen en distintas etapas, desde la construcción y corroboración del modelo en sí hasta su uso. Normalmente su uso es el culpable.
Toda solución a un problema de toma de decisiones se basa en determinados parámetros que se presumen como fijos. El análisis de sensibilidad es un conjunto de actividades posteriores a la solución que sirven para estudiar y determinar qué tan sensible es la solución a los cambios en las hipótesis. Estas actividades también se denominan análisis de estabilidad, análisis what-if o de hipótesis, modelación de escenarios, análisis de especificidad, análisis de incertidumbre, análisis de inestabilidad numérica, inestabilidad funcional y tolerancia, análisis de post optimalidad, aumentos y disminuciones admisibles y muchos otros términos similares que reflejan la importancia de esta etapa del proceso de modelación. Por ejemplo, análisis de sensibilidad no es el término típico empleado en la econometría para referirse al método de investigación de la respuesta de una solución frente a perturbaciones en los parámetros. En econometría, esto se denomina estática comparativa o dinámica comparativa, según el tipo de modelo en cuestión.
Se puede hacer frente a las incertidumbres de una manera más "determinista". Este abordaje tiene distintos nombres tales como "modelación de escenarios", "modelación determinista", "análisis de sensibilidad" y "análisis de estabilidad". La idea es generar, de manera subjetiva, una lista ordenada de incertidumbres importantes que supuestamente podrían tener un mayor impacto sobre el resultado final. Esto se lleva acabo antes de focalizarse en los detalles de cualquier "escenario" o modelo.
Resulta vital comprender la influencia de lo antedicho en el plan de acción sugerido por el modelo por las siguientes razones:
Pueden presentarse distintos niveles de aceptación (por el público en general, por los decisores, por las partes interesadas) a distintos tipos de incertidumbre.
Distintas incertidumbres tienen distintos impactos sobre la confiabilidad, robustez y eficiencia del modelo.
La relevancia del modelo (su correspondencia con la tarea) depende en gran medida del impacto de la incertidumbre sobre el resultado del análisis. Las sorpresas no forman parte de las decisiones óptimas sólidas.
Existen numerosos ejemplos de entornos donde esto es aplicable, tales como:
- Construcción de indicadores (económicos / ambientales)
- Análisis y pronóstico de riesgo (ambiental, financiero, de seguros,...)
- Optimización y calibración de modelos (per se)
A continuación, sigue una lista abreviada de las razones por las cuales se debe tener en cuenta el análisis de sensibilidad:
Toma de decisiones o desarrollo de recomendaciones para decisores:
- Para probar la solidez de una solución óptima. Las sorpresas no forman parte de las decisiones óptimas sólidas.
- Para identificar los valores críticos, umbrales, o valores de equilibrio donde cambia la estrategia óptima.
- Para identificar sensibilidad o variables importantes.
- Para investigar soluciones sub-óptimas.
- Para desarrollar recomendaciones flexibles que dependan de las circunstancias.
- Para comparar los valores de las estrategias de decisión simples y complejas.
- Para evaluar el riesgo de una estrategia o escenario.
Comunicación:
- Para formular recomendaciones más creíbles, comprensibles, contundentes o persuasivas.
- Para permitir a los decisores seleccionar hipótesis.
- Para comunicar una falta de compromiso a una única estrategia.
- El decisor debe incorporar algunas otras perspectivas del problema tal como perspectivas culturales, políticas, psicológicas, etc. en las recomendaciones del científico de administración.
Aumentar la comprensión o aptitud del sistema:
- Para estimar la relación entre las variables de entrada y las de salida.
- Para comprender la relación entre las variables de entrada y las de salida. Para desarrollar pruebas de las hipótesis.
Desarrollo del modelo:
- Para probar la validez o precisión del modelo.
- Para buscar errores en el modelo
- Para simplificar el modelo.
- Para calibrar el modelo.
- Para hacer frente a la falta o insuficiencia de datos.
- Para priorizar la adquisición de información.
Lista abreviada de casos en los que se debe considerar la realización de un análisis de sensibilidad:
- Con el control de los problemas, el análisis de sensibilidad puede facilitar la identificación de regiones cruciales en el espacio de los parámetros de entrada.
- En ejercicios de selección, el análisis de sensibilidad sirve para localizar algunos parámetros influyentes en sistemas con cientos de datos de entrada inciertos.
- Se utilizan técnicas de análisis de sensibilidad basados en varianza para determinar si un subconjunto de parámetros de entrada puede representar (la mayor parte de) la varianza de salida.
- El punto (3) puede utilizarse para la reducción del mecanismo (descartar o corregir partes no relevantes del modelo) y para la extracción de un modelo (construir un modelo a partir de otro más complejo). Ver también el problema de la "relevancia" del modelo: ¿los parámetros del conjunto de entrada del modelo son relevantes con respecto a la tarea del modelo?
- El punto (3) también puede utilizarse para la identificación del modelo identificando las condiciones experimentales para las cuales su capacidad para discriminar dentro del modelo se encuentra en su punto máximo.
- Al igual que en el punto (5), el análisis de sensibilidad puede utilizarse para la calibración del modelo, para determinar si los experimentos con sus incertidumbres relacionadas permitirán la estimación de los parámetros. Esto es particularmente útil frente a problemas mal condicionados (mal formulados).
- El análisis de sensibilidad puede complementarse con algoritmos de búsqueda / optimización; identificando los parámetros más importantes, el análisis de sensibilidad puede permitir que se reduzca la dimensionalidad del espacio donde se realiza la búsqueda.
- Como una herramienta de aseguramiento de calidad, el análisis de sensibilidad asegura que la dependencia de la salida (resultado) de los parámetros de entrada del modelo tenga una similitud física y una explicación.
- Para resolver un problema inverso, el análisis de sensibilidad sirve como una herramienta para extraer parámetros incorporados en modelos cuyos resultados no se correlacionan fácilmente con la entrada desconocida (por ejemplo en cinética química, para extraer las constantes cinéticas de sistemas complejos a partir del índice de rendimiento de los componentes).
- Para asignar recursos en el área de I&D de manera óptima, el análisis de sensibilidad muestra donde vale la pena invertir a fin de reducir el rango de incertidumbre del modelo.
- El análisis de sensibilidad puede determinar cuantitativamente qué parte de la incertidumbre de mi predicción se debe a incertidumbre paramétrica de la estimación y cuánto a incertidumbre estructural.
Errores de redondeo cometido por los gerentes: como siempre, se debe prestar atención al redondear el valor de los límites de los rangos de sensibilidad. El límite superior y el límite inferior deben redondearse hacia abajo y hacia arriba respectivamente para que sean válidos.
Análisis de sensibilidad vs. programación estocástica: el análisis de sensibilidad y las formulaciones de programación estocástica son los dos principales enfoques para manejar la incertidumbre. El análisis de sensibilidad es un procedimiento de post optimalidad que no puede influir en la solución. Sirve para investigar los efectos de la incertidumbre sobre la recomendación del modelo. Por otro lado, la formulación de programación estocástica introduce información probabilística acerca de los datos del problema, a pesar de los primeros momentos (es decir los valores esperados) de la distribución de la función objetivo con respecto a la incertidumbre. Esto ignora las evaluaciones de riesgo del decisor, caracterizadas por la varianza o el coeficiente de variación.
Cálculo de Rangos de Sensibilidad para Problemas Pequeños
Para calcular los rangos de sensibilidad de problemas de PL con 2 variables de decisión como máximo y/o 2 restricciones como máximo, puede probar alguno de los siguientes abordajes de fácil uso.La única restricción es que no se permiten restricciones de igualdad.Tener una restricción de igualdad implica degeneración, porque cada restricción de igualdad, por ejemplo, X1 + X2 = 1, significa dos restricciones simultáneas: X1 + X2 £ 1 , y X1 + X2 ³ 1. Entonces, la cantidad de restricciones obligatorias en tal caso será mayor a la cantidad de variables de decisión. Esto se denomina situación degenerada para la cual el análisis de sensibilidad normal no es válido.
Rango de Sensibilidad de Costos para Problemas de PL con dos Variables de Decisión
Volviendo al Problema del Carpintero, si cambiamos la ganancia de cada producto, cambia la pendiente de la función objetivo de igual valor (función iso). Para "pequeños" cambios, el óptimo permanece en el mismo punto extremo. Para cambios mayores, la solución óptima se desplaza a otro punto. Por consiguiente, tenemos que modificar la formulación y resolver un nuevo problema.
El problema es encontrar un rango para cada coeficiente de costos c(j), de la variable Xj, de manera que la solución óptima actual, es decir el punto extremo actual (esquina) siga siendo óptimo.
Para un problema de PL de 2 dimensiones, puede probar el sencillo abordaje que presentamos a continuación para saber cuál es la cantidad de aumento/disminución de cualquier coeficiente de la función objetivo (también conocidos como coeficientes de costos porque históricamente durante la Segunda Guerra Mundial, el primer problema de PL fue un problema de minimización de costos) a fin de mantener la validez de la solución óptima actual. La única condición requerida para este abordaje es que no se permiten restricciones de igualdad, ya que esto implicaría degeneración, para lo cual el análisis de sensibilidad tradicional no es válido.
Paso 1: Considere las únicas dos restricciones obligatorias de la solución óptima actual. Si hay más de dos restricciones obligatorias, hay degeneración, en cuyo caso el análisis de sensibilidad tradicional no es válido.
Paso 2: Perturbe el coeficiente de costos j° por el parámetro cj (esta es la cantidad desconocida de cambios).
Paso 3: Construya una ecuación correspondiente a cada restricción obligatoria, como figura a continuación:
(Costo Cj perturbado) / coeficiente de Xj en la restricción = Coeficiente de la otra variable en la función objetivo / coeficiente de esa variable de la restricción.
Paso 4: La cantidad de aumento admisible es el cj positivo menor posible, mientras que la disminución admisible es el cj negativo mayor posible obtenido en el Paso 3.
Fíjese que si no hay cj positivo (negativo), la cantidad de aumento (disminución) es ilimitada.
Advertencias:
- Recuerde que nunca debe dividir por cero. Dividir por cero es una falacia común en algunos libros de texto. Por ejemplo en Introduction to Management Science, de Taylor III, B., 6th Ed., Prentice Hall, 1999, the author, unfortunately, divides by zero on page 189.
Para mayores detalles y otras falacias comunes, visite el sitio Web The zero saga & confusions with numbers . Una pregunta para usted: ¿cuáles de estas afirmaciones son correctas y por qué?
a) cualquier número divido por cero es indefinido;
b) cero divido por cualquier número es cero; o
c) cualquier número dividido por sí mismo es 1
- Comúnmente se cree que se puede calcular el rango de sensibilidad al costo acotando la pendiente (perturbada) de la función objetivo (función iso) por las pendientes de las dos líneas resultantes de las restricciones obligatorias. Este método gráfico basado en las pendientes está descripto en de An Introduction to Management Science, by Anderson D., y Williams T., 9° Ed., West Publisher, 2000, (Sección 3.2). Lamentablemente, esto es confuso. Debería advertirse que este abordaje no es general y funciona si y sólo si los coeficientes no cambian de signo.
Por ejemplo, si aplicamos este abordaje en la construcción del rango de sensibilidad de los coeficientes de costos del siguiente problema;
Maximizar 5X1 + 3X2
Sujeta a: X1 + X2 £ 2, X1 - X2 £ 0, X1 ³ 0, X2 ³ 0
Obtenemos rangos incorrectos. Visite el sitio Web Myths and Counterexamples in Mathematical Programming para ver ilustraciones y una explicación de este anti-ejemplo.
El problema del carpintero:
Maximice 5X1 + 3X2
Sujeta a:
2X1 + X2 £ 40
X1 + 2X2 £ 50
X1 ³ 0
X2 ³ 0
Cálculo del incremento/disminución permisibles de C1 = 5: Las restricciones obligatorias son la primera y la segunda. Alterando este coeficiente de costo por c1 se obtiene 5 + c1. En el paso 3 se obtiene:
(5 + c1)/2 = 3/1, para la primera restricción, y (5 + c1)/1 = 3/2 para la segunda restricción. Resolviendo estas dos ecuaciones se obtiene: c1 = 1 y c1 = -3.5. Por lo tanto, el incremento permisible es 1, mientras que la disminución permisible es 1.5. Por lo tanto, mientras el primer coeficiente de costo C1 permanezca dentro del intervalo [ 5 - 3.5, 5 + 1] = [1.5, 6], continúa la solución óptima actual.
De modo similar, para el segundo coeficiente de costo C2 = 3 se obtiene el rango de sensibilidad [2.5, 10].
Consideremos el problema anterior con otro ejemplo:
Maximice 5X1 + 3X2
Sujeta a:
X1 + X2 £ 2
X1 - X2 £ 0
X1 ³ 0
X2 ³ 0
Cálculo del incremento/disminución permisibles de C1 = 5: Las restricciones obligatorias son la primera y la segunda. Alterando este coeficiente de costo por c1 se obtiene 5 + c1. En el paso 3 se obtiene:
(5 + c1)/1 = 3/1, para la primera restricción y (5 + c1)/1 = 3/(-1) para la segunda restricción. Resolviendo estas dos ecuaciones se obtiene: c1 = -2 y c1 = -8. Por lo tanto, la disminución permisible es 2, mientras que el incremento permisible es ilimitado. Por lo tanto, mientras el primer coeficiente de costo C1 permanezca dentro del intervalo [ 5 - 2, 5 + ¥] = [3, ¥], continúa la solución óptima actual.
De modo similar, para el segundo coeficiente de costo C2 = 3 se obtiene el rango de sensibilidad [3 - 8, 3 + 2] = [-5, 5].
Rango de sensibilidad del lado derecho para problemas de PL con dos restricciones como máximo
En el Problema del Carpintero, cuando se efectúan cambios menores en cualquiera de los recursos, la estrategia óptima (es decir, hacer el producto mixto) sigue siendo válida. Cuando los cambios son mayores, esta estrategia óptima cambia y el Carpintero debe, hacer todas las mesas o las sillas que pueda. Este es un cambio drástico de estrategia; por lo tanto, tenemos que revisar la formulación y resolver un nuevo problema.
Además de la información necesaria que antes se mencionó, también nos interesa saber cuánto puede vender (o comprar) el Carpintero de cada recurso a un precio (o costo) "razonable". Es decir, ¿hasta dónde se puede incrementar o disminuir el RHS(i) con un valor i fijo, mientras se mantiene la validez del precio sombra corriente del RHS(i)? Es decir, ¿hasta dónde se puede incrementar o disminuir el RHS(i) con un valor i fijo mientras se mantiene la solución óptima corriente para el problema dual?
Históricamente, el precio sombra se definió como la mejora en el valor de la función objetivo por incremento unitario en el lado derecho porque con frecuencia el problema se pone en la forma de mejora de maximización de utilidad (en el sentido de incremento).
Asimismo, con cualquier RHS, el precio sombra (también conocido como su valor marginal), es la cantidad de cambio en el valor óptimo proporcional a una unidad de cambio para ese RHS en particular. Sin embargo, en algunos casos no se permite cambiar tanto el RHS. El rango de sensibilidad del RHS proporciona los valores para los que el precio sombra tiene significado económico y permanece sin cambios.
¿Hasta dónde se puede incrementar o disminuir cada RHS individual manteniendo la validez de los precios sombra? Esta frase equivale a preguntar cuál es el rango de sensibilidad para el coeficiente de costo en el problema dual.
El dual del Problema del Carpintero es:
Minimice 40U1 + 50U2
Sujeta a:
2U1 + U2 ³ 5
U1 + 2U2 ³ 3
U1 ³ 0
U2 ³ 0
La solución óptima es U1 = 7/3 y U2 = 1/3 (que son los precios sombra).
El Problema del Carpintero:
Maximice 5X1 + 3X2
Sujeta a:
2X1 + X2 £ 40
X1 + 2X2 £ 50
X1 ³ 0
X2 ³ 0
Cálculo del Rango para RHS1: Las primeras dos restricciones son obligatorias, por lo tanto:
(40 + r1)/2 = 50/ 1, y (40 + r1) / 1 = 50/ 2.
De la resolución de estas dos ecuaciones se obtiene: r1 = 60 y r1 = -15. Por lo tanto, el rango de sensibilidad para el primer RHS en el problema del carpintero es: [40-15, 40 + 60] = [25, 100].
De modo similar, para el segundo RHS, se obtiene: [50 - 30, 50 + 30] = [20, 80].
Qué es la Regla del 100% (región de sensibilidad)
El rango de sensibilidad que se presentó en la sección anterior es un análisis del tipo "what-if" o de hipótesis del tipo de "un cambio por vez". Consideremos el problema del Carpintero; supongamos que queremos hallar los incrementos permisibles simultáneos de RHS ( r1, r2 ³ 0). Existe un método sencillo de aplicar que se conoce como "la regla del 100%" que establece que los precios sombra no cambian si se da la siguiente condición suficiente:
Aquí, 60 y 30 son los incrementos permisibles de los RHS, basados en la aplicación del análisis de sensibilidad ordinario. Es decir, siempre que el primer y el segundo RHS aumentan r1, y r2 respectivamente, mientras esta desigualdad continúe, los precios sombra para los valores del lado derecho permanecen sin cambios. Obsérvese que ésta es una condición suficiente porque, si se viola esta condición, entonces los precios sombra pueden cambiar o aún así seguir iguales. El nombre "regla del 100%" surge evidente cuando se observa que en el lado izquierdo de la condición, cada término es un número no negativo menor que uno, que podría representarse como un porcentaje de cambio permisible. La suma total de estos cambios no debería exceder el 100%.
Aplicando la regla del 100% a los otros tres cambios posibles en los RHS se obtiene:
La siguiente Figura ilustra la región de sensibilidad de ambos valores RHS como resultado de la aplicación de la regla del 100% al problema del Carpintero.
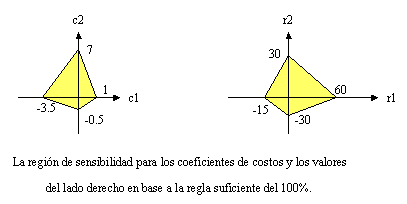
Desde un punto de vista geométrico, obsérvese que el poliedro con los vértices (60, 0), (0, 30), (-15, 0) y (0,-30) en la Figura es sólo un subconjunto de una región de sensibilidad más grande para los cambios en ambos RHS. Por lo tanto, permanecer dentro de esta región de sensibilidad es sólo una condición suficiente (no necesaria) para mantener la validez de los precios sombra actuales.
Pueden obtenerse resultados similares para los cambios simultáneos de los coeficientes de costos. Por ejemplo, supongamos que queremos hallar la disminución permisible simultánea en 1 y los incrementos en 2, , es decir, el cambio en ambos coeficientes de costo de 1 £ 0 y c2 ³ 0.
La regla del 100% establece que la base corriente sigue siendo óptima siempre que:
Donde 3.5 y 7 son la disminución y el incremento permisibles de los coeficientes de costo 1 y C2, respectivamente, que se hallaron anteriormente mediante la aplicación del análisis de sensibilidad ordinario. , respectively, that we found earlier by the application of the ordinary sensitivity analysis.
La Figura anterior también ilustra todas las otras posibilidades de incrementar/disminuir los valores de ambos coeficientes de costos como resultado de la aplicación de la regla del 100%, mientras se mantiene al mismo tiempo la solución óptima corriente para el problema del Carpintero.
Como otro ejemplo numérico, consideremos el siguiente problema:
Maximice 5X1 + 3X2
Sujeta a:
X1 + X2 £ 2
X1 - X2 £ 0
X1 ³ 0
X2 ³ 0
Quizás recuerden que ya hemos calculado los rangos de sensibilidad con un cambio por vez para este problema en la sección Cálculo de Rangos de Sensibilidad. El rango de sensibilidad para el primer coeficiente de costo es [ 5 - 2, 5 + ¥] = [3, ¥], mientras que para el segundo coeficiente de costo es [3 - 8, 3 + 2] = [-5, 5]. Se debería poder reproducir una figura similar a la anterior ilustrando todas las otras posibilidades de incrementar/disminuir ambos valores de coeficientes de costos como resultado de la aplicación de la regla del 100%, mientras al mismo tiempo se mantiene la solución óptima corriente para este problema.
Claramente, la aplicación de la regla del 100%, en la forma en que aquí se la presenta, es general y puede extenderse a cualquier problema de PL de mayor magnitud. Sin embargo, a medida que aumenta la magnitud del problema, este tipo de región de sensibilidad se reduce y por lo tanto, resulta menos útil para la gestión. . Existen técnicas más poderosas y útiles (que proporcionan condiciones necesarias y suficientes a la vez) para manejar cambios simultáneos dependientes (o independientes) de los parámetros. Para realizar un estudio abarcador de los distintos tipos de análisis de sensibilidad en PL con ejemplos numéricos ilustrativos, consúltese el siguiente artículo:
Arsham H., Perturbation analysis of general LP models: A unified approach to sensitivity, parametric tolerance, and more-for-less analysis, Mathematical and Computer Modelling, 12, 1437-1446, 1990.
Añadir una nueva restricción
El proceso: Introduzca la solución óptima corriente en la restricción recién añadida. Si la restricción no se viola, la nueva restricción NO afecta la solución óptima. De lo contrario, el nuevo problema debe resolverse para obtener la nueva solución óptima.Suprimir una restricción
El proceso: Determine si la restricción es obligatoria (es decir, activa, importante) hallando si el valor de holgura/excedente es cero. Si es obligatoria, la supresión puede cambiar la solución óptima corriente. Suprima la restricción y resuelva el problema. De lo contrario (si no es una restricción obligatoria), la supresión no afectará la solución óptima.Reemplazar una restricción
Supongamos que se reemplaza una restricción por una nueva. ¿Cuál es el efecto de este intercambio?El proceso: Determine si la restricción previa es obligatoria (es decir, activa, importante) hallando si el valor de holgura/excedente es cero. Si es obligatoria, el reemplazo puede afectar la solución óptima corriente. Reemplace la restricción y resuelva el problema. De lo contrario (si no es una restricción obligatoria), determine si la solución corriente satisface la nueva restricción. Si la satisface, entonces este intercambio no afectará la solución óptima. De lo contrario (si la solución corriente no satisface la nueva restricción), reemplace la restricción anterior por la nueva y resuelva el problema.
Añadir una variable (por ejemplo, introducir un nuevo producto)
El proceso: Construya la nueva restricción del problema solución óptima corriente es óptima), de lo contrario produzca el nuevo producto (la solución óptima corriente ya no es más óptima). Para determinar el nivel de dual. Inserte la solución dual en esta restricción. Si la restricción se satisface, NO produzca el nuevo producto (la producción del nuevo producto (es decir, una solución óptima mejor) resuelva el siguiente problema.Suprimir una variable (es decir, cancelar un producto)
El proceso: Si para la solución óptima corriente, el valor de la variable suprimida es cero, entonces la solución óptima corriente sigue siendo la óptima sin incluir la variable. De lo contrario, suprima la variable de la función objetivo y las restricciones, y luego resuelva el problema.Problema de asignación óptima de recursos
Como los recursos son siempre escasos, a los gerentes les preocupa el problema de la asignación óptima de los recursos. Se recordará que en el Problema del Carpintero se trataron ambos recursos como parámetros, es decir, como valores numéricos fijos:Maximice 5 X1 + 3 X2
Sujeta a:
2 X1 + X2 £ 40, restricción de mano de obra
X1 + 2 X2 £ 50, restricción de material
y ambas X1, X2 son no negativas.
Recordarán asimismo que habitualmente las restricciones se clasifican como restricciones del tipo de recurso o de producción. Es un hecho que en la mayoría de los problemas de maximización, las restricciones de recursos forman parte natural del problema, mientras que en el problema de minimización, las restricciones de producción son la parte más importante del problema.
Supongamos que desea hallar la mejor asignación del recurso mano de obra para el Carpintero. En otras palabras, ¿cuál es el mejor número de horas que el Carpintero debería asignar a su negocio?
Tomemos como R el número de horas asignadas, el cual se usará para determinar su valor óptimo. Por lo tanto, el modelo matemático es hallar R1, de modo tal que:
Maximice 5 X1 + 3 X2
Sujeta a:
2 X1 + X2 £ R1 restricción mano de obra
X1 + 2 X2 £ 50 restricción de material
y todas las variables X1, X2 y R1 son no negativas.
Obsérvese que ahora R1 se trata no como un parámetro sino como una variable de decisión. Es decir, la maximización se realiza con las tres variables, X1, X2 y R1:
Maximice 5 X1 + 3 X2
Sujeta a:
2 X1 + X2 - R1 £ 0 restricción de mano de obra
X1 + 2 X2 £ 50 restricción de material
y todas las variables X1, X2 y R1 son no negativas.
Con software de PL, la solución óptima es X1 = 50, X2 = 0, con una asignación óptima de la mano de obra de R1 = 100 horas. Así, el valor óptimo es $250.
Asimismo, obsérvese que el valor óptimo de asignación de recursos es siempre el mismo como límite superior del rango de sensibilidad RHS1 generado por el software.
Por ejemplo, el incremento permisible en el número de horas es 100 - 40 = 60 horas, con el adicional 250 - 110 = 140.
Incluso se puede obtener el precio sombra para este recurso usando esta información. El precio sombra es el índice de cambio en el valor óptimo con respecto al cambio en el lado derecho. Por lo tanto, (250 - 110)/(100 - 40) = 140/60 = 7/3, que es el precio sombra del RHS1, según se halló por otros métodos en las secciones anteriores.
Determinación de la mínima utilidad neta del producto
En la mayoría de los casos, la utilidad neta es un factor incontrolable en un entorno de negocios "tomador de precios". Es por ello que a los gerentes les importa conocer cuál es la utilidad neta mínima de cada producto determinado, que indica que su producción es rentable para empezar.Se recordará que en el Problema del Carpintero ambas utilidades netas ($5 y $3) fueron consideradas como entradas incontrolables, es decir, que eran valores determinados por el mercado:
Maximice 5 X1 + 3 X2
Sujeta a:
2 X1 + X2 £ 40 restricción mano de obra
X1 + 2 X2 £ 50 restricción material.
Y ambos, X1, X2, son no negativos.
Aquí, la estrategia óptima es X1 =10, X2 = 20, con un valor óptimo de $110.
Supongamos que el Carpintero desea conocer el valor mínimo del primer coeficiente en la función objetivo, que actualmente es $5, para poder producir con rentabilidad el primer producto (las mesas).
Supóngase que la utilidad neta mínima es c1 dólares; por lo tanto, el problema consiste en hallar c1, de manera tal que:
Maximice c1 X1 + 3 X2
Sujeta a:
2 X1 + X2 £ 40 restricción mano de obra
X1 + 2 X2 £ 50 restricción material.
Y todas las variables, X1, X2, c1, son no negativas.
Ahora, el problema dual del carpintero es:
Minimice 40 U1 + 50 U2
Sujeta a:
2U1 + 1U1 ³ c1 Utilidad neta de una mesa
1U1 + 2U2 ³ 3 Utilidad neta de una silla.
Y U1, U2, c1 son no negativas.
Se observa que ahora la utilidad neta c1 se trata como una variable de decisión. La minimización se hace sobre las tres variables; X1, X2 y c1:
Minimice 40 U1 + 50 U2
Sujeta a:
2U1 + 1U1 - c1 ³ 0
1U1 + 2U2 ³ 3
Y U1, U2, c1 son no negativas.
La implementación de este problema en el paquete de computación muestra que la solución óptima es U1 = $7/3, U2 = $1/3, y c1 = $1.5.
Se recordará que existen soluciones alternativas para este valor de frontera del rango de sensibilidad para el coeficiente de costo. La solución correspondiente al límite inferior se describe en el rango del análisis de sensibilidad del coeficiente de costo, calculado con anterioridad en el Problema del Carpintero. Por lo tanto, la mínima utilidad neta es siempre la misma que el límite inferior del rango de sensibilidad del coeficiente de costo generado por el software.
Indicadores de metas
En la mayoría de las situaciones de la vida real, al decisor puede no interesarle la optimización, y desear en cambio alcanzar un cierto valor para la función objetivo. A la mayoría de los gerentes les satisface una solución "suficientemente buena". A este problema se lo conoce como "satisfacer" el problema de "alcanzar la meta".Una de las razones por las cuales los gerentes de empresas sobrestiman la importancia de la estrategia óptima es que las organizaciones con frecuencia usan indicadores como "sustitutos" para satisfacer sus necesidades inmediatas. La mayoría de los gerentes prestan atención a indicadores tales como la utilidad, el flujo de fondos, el precio de la acción, etc. que indican más una supervivencia que una meta de optimización.
Para resolver el problema de alcanzar la meta, se debe primero añadir la meta del conjunto de restricciones. Para convertir el problema de alcanzar la meta en un problema de optimización, se debe crear una función objetivo ficticia. Podría ser una combinación lineal del subconjunto de variables de decisión. Si se maximiza esta función objetivo se obtendrá una solución factible (si es que existe). Si se minimiza, se podría obtener otra (habitualmente en el otro "lado" de la región factible). Se podría optimizar con diferentes funciones objetivas.
Otro abordaje es usar modelos de "Programación de Metas" que manejan con precisión problemas de satisfacción de restricciones sin necesariamente tener un solo objetivo. Básicamente, consideran medidas de violación de restricciones e intentan minimizarlas. Se pueden formular y resolver modelos de programación de metas en PL tradicional, usando códigos de solución de PL tradicionales.
En el algoritmo de solución sin variables artificiales se puede usar una función objetivo ficticia de cero pero no en algunos paquetes de software, tales como el Lindo. Con los paquetes de software se puede maximizar o minimizar cualquier variable como una función objetivo.
Ejemplo numérico
Considere el Ejemplo 1 en la sección Inicialización del Método Símplex en un sitio asociado a éste. En lugar de maximizar ahora queremos alcanzar una meta de 4, es decir,
Meta: -X1 + 2X2 = 4
sujeta a:
X1 + X2 ³ 2,
-X1 + X2 ³ 1,
X2 £ 3,
y X1, X2 ³ 0.
Si se añade esta meta al conjunto de restricciones y se convierten las restricciones a la forma de igualdad se obtiene:
X1 + X2 - S1 = 2, -X1 + X2 - S2 = 1, X2 + S3 = 3, y
X1, X2, S1, S2, S3 ³ 0.
Una solución es X1 = 2, X2 = 3, S1 = 3, S2 = 0, y S3 = 0.
Para obtener detalles sobre los algoritmos de soluciones visite el sitio Web Artificial-Free Solution Algorithms.
Cálculo de minimax y maximin en una sola corrida
Supongamos que quiere hallar el peor de varios valores de funciones objetivos definidas con un conjunto común de restricciones en una sola corrida de computación.Como aplicación, supongamos que en el Problema del Carpintero, sin pérdida de generalidad, hay tres mercados con funciones objetivos de 5X1 + 3X2, 7X1 + 2X2, y 4X1 + 4X2, respectivamente. Al carpintero le interesa conocer el peor mercado. Es decir, la solución del siguiente problema:
El problema del minimax:
Min Max {5X1 + 3X2, 7X1 + 2X2, 4X1 + 4X2}
Sujeta a:
2 X1 + X2 £ 40
X1 + 2 X2 £ 50
Y ambos, X1, X2, son no negativos.
El Problema del Minimax equivale a:
Maximice y
Sujeta a:
y £ 5x1 + 3X2
y £ 7X1 + 2X2
y £ 4X1 + 4X2
2X1 + X2 £ 40
X1 + 2X2 £ 50
Y todas las variables, X1, X2, y, son no negativas.
Si se toman todas las variables a la izquierda de las restricciones y este problema se implementa en el paquete de computación, la solución óptima es X1 = 10, X2 = 20, y = $110. Esto significa que el primero y el segundo mercados son los peores (porque la primera y la segunda restricciones son obligatorias) aportando sólo $110 de utilidad neta.
De modo similar, se puede resolver el minimax de varias funciones objetivos en una sola corrida.
Situaciones de más por menos y menos por más
Considere el siguiente problema de PL de producción:
Maximice X1 + 3X2 + 2X3,
sujeta a: X1 + 2X2 + X3 = 4, 3X1 + X2 + 2X3 = 9, todas Xi son no negativas.
Los totales de mano de obra son 4 y 9. El valor óptimo para este problema es $7.
Ahora, si se cambia la segunda mano de obra disponible de 9 por 12, el valor óptimo sería $4. Es decir, que se ha trabajado más horas por menos utilidad.
Esta situación surgen frecuentemente y se conoce como "La Paradoja de Más por Menos". El recurso número 2 tiene un precio sombra negativo!
Para hallar el mejor número de horas se debe trabajar para maximizar el ingreso, resolviendo la siguiente PL paramétrica:
Maximice X1 + 3X2 + 2X3
sujeta a: X1 + 2X2 + X3 = 4, 3X1 + X2 + 2X3 = L , L, y todas Xi son no negativas.
Con LINDO (o WinQSB) se debe resolver:
Maximice X1 + 3X2 + 2X3
sujeta a: X1 + 2X2 + X3 = 4, 3X1 + X2 + 2X3 - L = 0.
La L óptima es 8 horas, y el valor óptimo es $8!
La condición necesaria y suficiente para que se dé la situación de más por menos/menos por más es que existan restricción(es) de igualdad con precio(s) sombra negativos para los valore(s) RHS.
Para obtener más información sobre ésta y otras paradojas visite:
Counterexamples and Explanations for LP Myths
El Método Simplex Clásico
Introducción
El método gráfico resulta limitado cuando se resuelven problemas de PL que tienen una o dos variables de decisión. Sin embargo, este proporciona una clara ilustración de donde se encuentran la región de factibilidad y de no-factibilidad, así como también de los vértices. El tener una comprensión visual del problema ayuda a un mejor proceso de pensamiento racional del mismo. Por ejemplo, hemos aprendido que: si una PL tiene una región de factibilidad no-vacía y conectada, la solución óptima siempre se encuentra en uno de los vértices de la región de factibilidad (una esquina.) Por lo tanto, lo que se necesita hacer es encontrar todos puntos de intercepción (vértices), ver cuales se encuentran dentro del área de factibilidad, y luego examinar cada uno de ellos para cual proporciona la solución óptima. Ahora, mediante el uso de los conceptos de Geometría Analítica podremos sobrellevar estas limitaciones de la visión humana. El método algebraico esta diseñado para extender los resultados del método gráfico a un problema de PL multidimensional.
Método Algebraico:
Los modelos de PL con variables de decisión multidimensional
Estamos interesados en resolver el siguiente problema general:
Max( ó Min) C.X
sujeto a:
AX £ a
BX ³ b
DX = d
con la posibilidad de algunas variables restringidas: algunos Xi's ³ 0, algunos Xi's £ 0, y todos los demás sin restricción en el signo.
Es utilizada la notación común: C = {Cj} para los coeficientes de la función objetivo (conocidos como los coeficientes de costo dado que históricamente, la primera PL fue un problema de minimización de costos), y X = {Xj } se utiliza para las variables de decisión.
A continuación presentamos el procedimiento de cuatro pasos para la solución algebraica del algoritmo:
- Construcción de los límites del conjunto de restricciones: Transformar todas las desigualdades (excepto la condición de restricción de cada variable, si existe alguna) a igualdades, mediante la adición o sustracción de variables de exceso o defecto. La construcción de los límites de las variables de las variables restringidas es incluido en el próximo paso.
- Encontrar Todos los Vértices: Si el número de variables (incluyendo las de exceso y defecto) son mayores al número de ecuaciones, proceda a hacer ceros el siguiente número de variables:
[(Número total de variables incluyendo las de exceso y defecto) – (Número de ecuaciones)] Las variables llevadas a cero son las variables de exceso y defecto y las variables restringidas (cualquier Xi's ³ 0, ó Xi's £ 0) solamente. Luego de llevar todas estas variables a cero, proceda a encontrar las otras variables mediante la resolución del sistema cuadrado de ecuaciones.
Note que si Xi ³ 0, entonces podría ser escrito como Xi - Si = 0, llevando los Si correspondientes a cero significa que Xi = 0, por lo tanto, no es necesario introducir explícitamente variables de exceso y defecto. Adicionalmente, note que cuando cualquier Xi no esta restringido en el signo, este no adiciona una restricción.
- Comprobar la Factibilidad: Todas las variables de defecto o exceso deben ser no-negativas, y compruebe por la condición de restricción (si existe alguna) en cada variable. Cada solución factible es llamada una Solución Factible Básica, la cual es el punto en cada esquina de la región de factibilidad.
- Seleccionar una Esquina Optima: Entre todas las soluciones factibles (i.e., puntos en las esquinas factibles), encuentre el óptimo (si existe alguno) evaluando cada uno en la función objetivo. Podrían existir soluciones óptimas múltiples.
Recuerde que: un sistema lineal AX=b tiene una solución si y solo si el rango de A es igual al rango de la matriz argumento (A,B).
Definiciones a Saber:
Cada solución para cualquier sistema de ecuaciones es llamada una Solución Básica (SB). Todos las SB, que son factibles se les llama Soluciones Factibles Básicas (SFB).
En cada solución básica, las variables, que usted igualo a cero, son llamadas las Variables No-Básicas (VNB), todas la otras variables que se calcularos mediante el sistema de ecuaciones son llamadas Variables Básicas (VB).
Note que, la lista de las variables de decisión, las cuales son las VB para una solución óptima, son absolutamente disponibles en la tabla de soluciones óptimas en QSB.
Los defectos son los sobrantes de insumos. Los excesos son los sobrantes en la producción.
Número de Soluciones Básicas: Después de convertir todas las inigualdades en igualdades, dejemos que T = el número total de variables, incluyendo las de exceso y defecto, E = Número de ecuaciones, y R = el número total de las variables de exceso y defecto, así como también las variables de decisiones restringidas, por lo que el número máximo de soluciones básicas es:
donde ! significa Factoriales. Por ejemplo, 4 ! = (1)(2)(3)(4) = 24. Note que por definición 0 ! = 1.
Note que, si E > T ó T > R + E, la formulación inicial de la PL podría estar equivocada. Los remedios para las acciones correctivas son discutidos en la sección El Lado Oscuro de la PL: Herramientas para la Validación de Modelos.
El resultado principal: Si un problema de PL no tiene solución(es) acotadas, el método algebraico generará las soluciones.
Ejemplo 1 : Un Problema sin Ninguna Variable Restringida:
Max X1 + X2
sujeto a:
X1 + X2 ³ 10
X1 £ 8
X2 £ 12
Introduciendo las variables d defecto y exceso, obtenemos:
X1 + X2 - S1 = 10
X1 + S2 = 8
X2 + S3 = 12
Para este problema E = 3, T = 5, R = 3, por lo tanto, existen como máximo 3! / [2! . (3 - 2)! ] = 3 soluciones básicas. Para encontrar las soluciones básicas, sabemos que existen 3 ecuaciones con 5 incógnitas, dejando cualquier 2 = 5 - 3 variables de exceso o defecto a cero, y luego resolviendo el sistema de ecuaciones resultante de 3 incógnitas, obtenemos:
| S1 | S2 | S3 | X1 | X2 | X1 + X2 |
| 0 | 0 | 10 | 8 | 2 | 10 |
| 10 | 0 | 0 | 8 | 12 | 20* |
| 0 | 10 | 0 | -2 | 12 | 10 |
La solución óptima es S1= 10, S2 = 0, S3 = 0, X1 = 8, X2 = 12, con un valor óptimo de 20.
Ejemplo 2: Un Problema con Una variable Restringida:
El siguiente problema es atribuido a Andreas Enge, y Petra Huhn.
Maximizar 3X1 + X2 - 4X3
sujeto a:
X1 + X2 - X3 =1,
X2 ³ 2,
X1 ³ 0
Luego de agregar la variable de exceso, tenemos:
Maximizar 3X1 + X2 - 4X3
sujeto a:
X1 + X2 - X3 =1,
X2 - S1 = 2,
Este problema de PL no puede ser resuelto por el método gráfico. Sin embargo, el método algebraico es general en el sentido que no pone ninguna limitación en la dimensionalidad del problema. Note que tenemos dos ecuaciones con una variable de exceso, y una variable de decisión restringida. Los parámetros para este problema son: T= 4, R = 2, y E = 2. Esto nos proporciona el número total de soluciones básicas posibles: 2! / [(2!). (0!)] = 1. Haciendo las variables X1 y de exceso iguales a cero:
| X1 | X2 | X3 | S1 | 3X1 + X2 -4X3 | |
| 0 | 2 | 1 | 0 | -2* |
Por lo tanto la solución óptima es X1 = 0, X2 = 2, X3 = 1, con un valor óptimo de -2.
Ejemplo 3: El Problema del Carpintero:
Introduciendo las variables de exceso y defecto para convertir todas las inigualdades en igualdades, tenemos:
2X1 + X2 + S1 = 40
X1 + 2X2 + S2 = 50
Aquí tenemos 2 ecuaciones con 4 incógnitas. Dado que las variables X1 y X2 son ambas restringidas, debemos llevar otras dos variables incluyendo estas dos a cero. Resolviendo el sistema de seis ecuaciones resultante, tenemos:
| S1 | S2 | X1 | X2 | 5X1 + 3X2 | |
| 0 | 0 | 10 | 20 | 110* | |
| 0 | -30 | 0 | 40 | no-factible | |
| 0 | 30 | 20 | 0 | 100 | |
| 15 | 0 | 0 | 25 | 75 | |
| -60 | 0 | 50 | 0 | no-factible | |
| 40 | 50 | 0 | 0 | 0 |
Por lo tanto, de la tabla anterior, obtenemos que la solución óptima es S1= 0, S2 = 0, X1 = 10, X2 = 20, con un valor óptimo de $110.
Ejemplo 4: Un Problema con Restricciones Mixtas:
Min X1 + 2X2
sujeto a:
X1 + X2 ³ 4
-X1 + X2 £ 2
X1 ³ 0, y X2 son no-restringidas en signo.
Introduciendo las variables de exceso y defecto, tenemos:
X1 + X2 - S1 = 4
-X1 + X2 + S2 = 2
Aquí tenemos 2 ecuaciones con 4 incógnitas. Dado que solo X1 es restringida, debemos hacer cero por lo menos dos de las variables S1, S2, y X1. Resolviendo el sistema de seis ecuaciones resultante, tenemos:
| X1 | X2 | S1 | S2 | X1 + 2X2 | |
| 0 | 4 | 0 | -2 | no-factible | |
| 0 | 2 | -2 | 0 | no-factible | |
| 1 | 3 | 0 | 0 | 7* |
Por lo tanto, de la tabla anterior vemos que la solución óptima es X1 = 1, X2 = 3, S1= 0, S2 = 0, con un valor óptimo de 7.
Ejemplo 5: Un Problema de Transporte:
El objetivo es encontrar la forma mas efectiva de transportar bienes. La oferta y demanda de cada origen (por ejemplo, almacenes) O1, O2 y destinos (por ejemplo, mercados) D1 y D2, junto a los costos unitarios de transporte se encuentran resumidos en la tabla siguiente:
| La Matriz de Costos Unitarios de Transporte | ||||
| D1 | D2 | Oferta | ||
| O1 | 20 | 30 | 200 | |
| O2 | 10 | 40 | 100 | |
| Demanda | 150 | 150 | 300 | |
Dejemos que los Xij denoten la cantidad de transportación que sale del origen i al destino j. La formulación de la PL del problema de minimización del costo total de transporte es:
Min 20X11 + 30X12 + 10X21 + 40X22
sujeto a:
X11 + X12 = 200
X21 + X22 = 100
X11 + X21 = 150
X12 + X22 = 150
todos los Xij ³ 0
dado que este problema de transporte es balanceado (oferta total = demanda total), todas las restricciones están en forma de igualdad. Adicionalmente, todas las restricciones son redundantes (agregando dos restricciones cualquiera y sustrayendo alguna otra obtendríamos la restante.) Eliminemos una restricción de tal forma que el problema se reduce a:
Min 20X11 + 30X12 + 10X21 + 40X22
sujeto a:
X11 + X12 = 200
X21 + X22 = 100
X11 + X21 = 150
para todos los Xij ³ 0
Este problema de PL no puede ser resuelto por el método gráfico. Sin embargo el método algebraico no tiene limitaciones en las dimensiones del PL. Note que tenemos tres ecuaciones con cuatro variables de decisión restringidas. Haciendo cualquiera de las variables cero, tenemos:
| X11 | X12 | X21 | X22 | Costo Total de Transporte |
| 0 | 200 | 150 | -50 | no-factible |
| 200 | 0 | -50 | 150 | no-factible |
| 150 | 50 | 0 | 100 | 8500 |
| 50 | 150 | 100 | 0 | 6500* |
Por lo tanto, la estrategia óptima es X11 = 50, X12 = 150, X21 = 100, y X22 = 0, con por lo menos un coste total de transporte de $6,500.
Ejemplo 6: Un Problema con Muy Pocas Restricciones:
Asi como en nuestro ejemplo anterior, considere el problema siguiente:
Max X1 + X2
sujeto a:
X1 + X2 £ 5
Introduciendo la variable de exceso tenemos:
X1 + X2 + S1 = 5
Los parámetros para este problema son: T = 3, R = 1, y E = 1. Esto proporciona el número total de soluciones básicas posibles 1! / [(1!). (0!)] = 1. Haciendo la variable de exceso cero, tenemos esta ecuación simple X1 + X2 = 5 con dos variables a resolver. Por lo tanto, no existen esquinas; adicionalmente, la región de factibilidad no se encuentra definida. Sin embrago, cualquier solución arbitraria tal y como X1 = 0, X2 = 5 es una solución óptima al problema de PL, con un valor óptimo de 5.
Pivoteando Operaciones en Filas
Como usted recuerda, el método algebraico envuelve el resolver varios sistemas de ecuaciones lineales. Cuando el problema de PL tiene varias variables y restricciones, el resolver muchos sistemas de ecuaciones manualmente se vuelve tedioso y en algunos casos cuando son problemas de gran escala, se hace imposible de resolverlos. Por lo tanto, necesitamos que las computadoras hagan los cálculos por nosotros. Uno de los algoritmos o aproximaciones computarizadas para resolver sistemas de ecuaciones lineales es conocido como las operaciones de pivoteo de Gauss-Jordan (GJ.)El pivoteo de GJ será también requerido posteriormente cuando utilicemos el Método Simplex, por lo tanto, ahora es el momento preciso para desarrollar los hábitos necesarios para los tiempos futuros.
El pivoteo utiliza operaciones en fila (conocido como las operaciones en fila de Gauss-Jordan) para cambiar una matriz de entrada (la pivote) a "1", y luego cambiar todas las otras entradas en la columna pivote a cero.
Una vez que el pivote es elegido, las operaciones de pivotaje en fila debe ser como sigue:
Paso 1: Hacer un pivote "1" mediante la división de toda la fila pivote por el valor del pivote.
Paso 2: Hacer el resto de la columna pivote ceros agregando a cada fila a múltiplo confiable de la fila pivote.
Note: El número cambiando a "1" llamado pivote, es usualmente encerrado en círculo, nunca puede ser cero. Si este valor es cero, intercambie esta fila con otra fila mas abajo que tenga un elemento diferente de cero en esa columna (sino existe ninguno, entonces la conversión será imposible.)
Un Ejemplo Numérico: Utilizando la operación de filas de Gauss-Jordan, resuelva el siguiente sistema de ecuaciones:
2X1 + X2 + X3 = 3
X1 + 3X3 = 1
2X1 + X2 = 2
El objetivo es convertir los coeficientes del sistema de ecuaciones en la siguiente matriz identidad. Los resultados de los elementos del Lado de la Mano Derecha (LMD) (?) proporcionan la solución (si esta existe.)
| 1 | 0 | 0 | ? |
| 0 | 1 | 0 | ? |
| 0 | 0 | 1 | ? |
Paso 2. En cada columna:
a) Primero obtenga 1 en la fila apropiada mediante la multiplicación del recíproco. Note: Si existe un valor cero en esta posición, intercambie con una fila mas abajo en la en la cual se encuentre un valor no-cero (si es posible.)
b) Reduzca todos los otros valores de la columna a cero mediante la adición del múltiplo apropiado correspondiente desde la fila que contiene el uno, a cada fila subsiguiente.
Apliquemos el procedimiento anterior a nuestro ejemplo numérico.
Notaciones: Fila vieja [ ], Fila nueva { }. Colocando estas dos matrices una junto a la otra, la matriz argumentada es:
|
Fila
#
|
Operaciones
|
Resultados
|
LMD
|
||
|
1
|
2
|
1
|
1
|
3
|
|
|
2
|
1
|
0
|
3
|
1
|
|
|
3
|
2
|
1
|
0
|
2
|
|
|
1
|
[1]/2
|
1
|
1/2
|
1/2
|
3/2
|
|
2
|
-1{1}+[2]
|
0
|
-1/2
|
5/2
|
-1/2
|
|
3
|
-2{1}+[3]
|
0
|
0
|
-1
|
-1
|
|
1
|
(-1/2){2}+[1]
|
1
|
0
|
3
|
1
|
|
2
|
[2]/(-1/2)
|
0
|
1
|
-5
|
1
|
|
3
|
(0){2}+[3]
|
0
|
0
|
-1
|
-1
|
|
1
|
(-3){3}
+ [1]
|
1
|
0
|
0
|
-2
|
|
2
|
(5){3}
+ [2]
|
0
|
1
|
0
|
6
|
|
3
|
[3]/(-1)
|
0
|
0
|
1
|
1
|
La solución es X1 = -2, X2 = 6, y X3 =1, la cual puede ser verificada mediante sustituciones.
Visite adicionalmente las páginas web Resolviendo un sistema de ecuaciones lineales, Máquina Pivote, Resolver un Sistema de Ecuaciones Lineales, y El Módulo de Ecuador The Equator Module.
El Método Simplex
El Método Simplex es otro algoritmo para resolver problemas de PL. Recuerde que el método algebraico proporciona todos los vértices incluyendo aquellos que no son factibles. Por lo tanto, esta no es una manera eficiente de resolver problemas de PL con numerosas restricciones. El Método Simplex es una modificación del método algebraico, el cual vence estas deficiencias. Sin embargo, el Método Simplex tiene sus propias deficiencias. Por ejemplo, este requiere que todas las variables sean no-negativas (³ 0); Además, todas las demás restricciones deben estar en la forma £ con un LMD de valores no-negativos.Así como el Método Algebraico, el método simplex es una solución algorítmica tabular. Sin embargo, cada tabla (de iteración) en el método simplex corresponde a un movimiento desde un Conjunto Básico de Variables (CBV) (puntos extremos ó esquinas) a otro, asegurándose que la función objetivo mejore en cada iteración hasta encontrar la solución óptima.
La presentación del método simplex no es universal. En la Costa Oeste de los Estados Unidos, profesores disfrutan resolviendo problemas de minimización, mientras que en la Costa Este se prefiere la maximización. Igualmente dentro de estos dos grupos usted encontrará diferentes presentaciones de las reglas del método simplex. El procedimiento siguiente describe todos los pasos envueltos en la aplicación de la solución algorítmica del método simplex:
- Convertir la PL a la forma siguiente:
Convierta el problema de minimización a un problema de maximización (mediante la multiplicación por –1 de la función objetivo).
Todas las variables deben ser no-negativas.
Todos los valores al LMD deben ser no-negativos (multiplique ambos lados por -1, si es necesario).
Todas las restricciones deben estar en la forma £ (excepto las condiciones de no-negatividad).Restricciones no estrictamente iguales ó ³ son permitidas.
Si esta condición no puede ser satisfecha, utilice la Inicialización del Método Simples: Libre-Artificialidad. - Convierta las restricciones £ a igualdades mediante la adición de diferentes variables de exceso para cada una de ellas.
- Construya la tablatura simplex inicial con todas las variables de exceso en CBV. La última fila en la tabla de iteración contiene el coeficiente de la función objetivo (fila Cj.)
- Determine si la tabla de iteración actual es óptima. Es decir: :
Si todos los valores al LMD son no-negativos (llamada, condición de factibilidad)
Si todos los elementos de la última fila, es decir la fila Cj, son no-positivos (llamado condición de optimalidad).Si la respuesta a ambas preguntas es Sí, entonces deténgase. La tabla de iteración actual contiene una solución óptima.
De otra forma, proceda al próximo paso. - Si el CBV actual es no es óptimo, determine cual variable no-básica debería convertirse en variable básica y viceversa. Para encontrar la nueva CBV con un mejor valor de función objetivo, realice el siguiente procedimiento:
- Identifique la variable entrante: Esta es la que posee el valor positivo Cj más grande (En el caso de que dos valores sean iguales en esta condición, seleccione el valor mas a la izquierda de las columnas.)
- Identifique la variable saliente: Esta es la variable con el ratio en columna no-negativa más pequeño (para encontrar los ratio en columnas, divida los LMD de las columnas entre la variable de columna entrante, siempre que sea posible). En caso de que existan dos valores iguales, seleccionamos la variable correspondiente al valor mas arriba de la columna igualada.)
-
Generar la nueva tabla de iteración: Realice la operación de pivoteo de Gauss-Jordan para convertir la columna entrante en un vector columna identidad (incluyendo los elementos de la fila Cj.)
Siga al paso 4.
- Identifique la variable entrante: Esta es la que posee el valor positivo Cj más grande (En el caso de que dos valores sean iguales en esta condición, seleccione el valor mas a la izquierda de las columnas.)
Una pequeña discusión acerca de la estrategia del método simplex: Al comienzo del procedimiento simplex; el conjunto de supuestos están constituidos por las variables de exceso (holgura.) Recuerde que el primer CBV contiene solo variables de exceso. La fila Cj presenta un incremento en el valor de la función objetivo el cual resultará si una unidad de la variable j-ésima columna correspondiente fue traída en los supuestos. Esta fila responde la pregunta: ¿Podemos mejorar la función objetivo si nos movemos a una nueva CBV? Llamaremos a esta la fila indicadora (dado que esta indica si la condición de optimalidad esta satisfecha).
El criterio para ingresar una nueva variable en el CBV causará el incremento por unidad mas alto de la función objetivo. El criterio para remover una variable del CBV actual se mantiene factible (asegurándose que el nuevo LMD, después de los no-negativos restantes.)
Advertencia: Siempre que durantes las iteraciones en el Simplex tengan un LMD negativo, significa que se ha seleccionado la variable saliente errada. El mejor remedio es comenzar de nuevo.
Note que existe una solución a cada tabla de iteración en el simplex. Los valores numéricos de las variables básicas son los valores de LMD, mientras que las otras variables (no-básicas) son siempre iguales a cero.
Interpretación Geométrica del Método Simplex: El método simplex siempre comienza al origen (esquina o punto extremo) y luego salta de esquina a esquina hasta que encuentra el punto extremo óptimo (si está bordeado.) Por lo tanto, en cada una de las iteraciones del simplex, estamos buscando una mejor solución entre los vértices de un Simplex. un simplex en un espacio n-dimensional es la forma más fácil teniendo n + 1 vértices. Por ejemplo, un triangulo es un simplex de espacio de 2 dimensiones mientras que una pirámide es un simplex en un espacio de 3 dimensiones. Estos movimientos pueden ser observados cuando se corresponde cada tabla de iteración del simplex con un punto extremo específico en el método gráfico, por ejemplo en el problema del carpintero, así como se muestra a continuación:
Las Recetas Numéricas sostienen que el algoritmo Simplex es ‘casi siempre’ O(max(N,M)), lo cual significa que el número de iteraciones es factor del número de variables ó restricciones, el que sea mas grande.
Un Ejemplo Numérico: El Problema del Carpintero
Maximizar 5X1 + 3X2
Sujeto a:
2X1 + X2 £ 40
X1 + 2X2 £ 50
y ambos X1, X2 son no-negativos.
Luego de agregar las dos variables de exceso S1 y S2, el problema se hace equivalente a:
Maximizar 5X1 + 3X2
Sujeto a:
2X1 + X2 + S1 = 40
X1 + 2X2 + S2 = 50
Y las variables X1, X2, S1, S2 son todas no-negativas.
la tabla de iteración inicial es:
| CBV | X1 | X2 | S1 | S2 | LMD | Ratio de Columna (C/R) | |
|---|---|---|---|---|---|---|---|
| S1 | [2] | 1 | 1 | 0 | 40 | 40/2 | |
| S2 | 1 | 2 | 0 | 1 | 50 | 50/1 | |
| Cj | 5 | 3 | 0 | 0 |
La solución mostrada por la tabla de iteración es: S1 = 40, S2 = 50, X1 = 0, y X2 = 0. Esta solución es el origen, mostrada en nuestro método gráfico.
Esta tabla de iteración no es óptima dado que algunos elementos Cj son positivos. La variable entrante es X1 y la saliente es S1 (mediante la prueba de C/R). El elemento pivote se encuentra entre las llaves ({}). Luego de pivotear, tenemos:
| CBV | X1 | X2 | S1 | S2 | LMD | Ratio de Columna (C/R) | |
|---|---|---|---|---|---|---|---|
| X1 | 1 | 1/2 | 1/2 | 0 | 20 | 20/(1/2)=40 | |
| S2 | 0 | [3/2] | -1/2 | 1 | 30 | 30/(3/2)=10 | |
| Cj | 0 | 1/2 | -5/2 | 0 |
La solución para esta tabla de iteración es: X1 = 20, S2 = 30, S1 = 0, y X2 = 0. Esta solución es el punto extremo (20, 0), mostrado en nuestro método gráfico.
Esta tabla de iteración no es óptima dado que algunos elementos Cj son positivos. La variable entrante es X2 y la saliente es S2 (mediante la prueba de C/R). El elemento pivote se encuentra entre las llaves ({}). Luego de pivotear, tenemos:
| CBV | X1 | X2 | S1 | S2 | LMD | |
|---|---|---|---|---|---|---|
| X1 | 1 | 0 | 2/3 | -1/3 | 10 | |
| X2 | 0 | 1 | -1/3 | 2/3 | 20 | |
| Cj | 0 | 0 | -7/3 | -1/3 |
La solución para esta tabla de iteración es: X1 = 10, X2 = 20, S1 = 0, y S2 = 0. Esta solución es el punto extremo (10, 20), mostrado en nuestro método gráfico.
Esta tabla de iteración es óptima dado que todos los elementos Cj son no-positivos y todos los LMD son no-negativos. La solución óptima es X1 = 10, X2 = 20, S1 =0, S2 = 0. Para encontrar el valor óptimo, sustituya estos valores en la función objetivo 5X1 + 3X2 = 5(10) + 3(20) = $110.
Visite también las páginas web tutOR, El Lugar Simplex, La Máquina Simplex, y Explorador -PL.
Programas lineales generales con enteros
La PL estándar asume que las variables de decisión son continuas. Sin embargo, en muchas aplicaciones, los valores fraccionarios pueden no servir de mucho (por ej., 2,5 empleados). Por otra parte, como a esta altura ya saben, como los programas lineales con enteros son más difíciles de resolver, quizás se pregunten para qué la molestia. ¿Por qué no simplemente usar un programa lineal estándar y redondear las respuestas a los enteros más cercanos? Desafortunadamente, esto genera dos problemas:
- La solución redondeada puede no ser factible, y
- El redondeo puede no dar una solución óptima.
Max 11X1 + 10X2
S.T. 2X1 + X2 £ 12
X1 - 3X2 ³ 1
END
GIN X1
GIN X2
La salida después de siete iteraciones es:
VALOR DE LA FUNCION OBJETIVO
1) 66.00000
VARIABLE VALOR COSTO REDUCIDO
X1 6.000000 -11.000000
X2 0.000000 -10.000000
FILA HOLGURA O EXCEDENTE
2) 0.000000
3) 5.000000
Si no hubiéramos especificado X1 y X2 como enteros generales en este modelo, LINDO no habría hallado la solución óptima de X1 = 6 y X2 = 0. En cambio, LINDO habría considerado a X1 y X2 como continuos y habría llegado a la solución X1 = 5.29 y X2 = 1.43.
Observen asimismo que el simple redondeo de la solución continua a los valores enteros más próximos no da la solución óptima en este ejemplo. En general, las soluciones continuas redondeadas pueden no ser las óptimas y, en el peor de los casos, no son factibles. Sobre esta base, uno se puede imaginar que puede demandar mucho tiempo obtener la solución óptima en un modelo con muchas variables de enteros. En general, esto es así, y les convendrá utilizar la característica GIN sólo cuando es absolutamente necesario.
Como último comentario, el comando GIN también acepta un argumento de valor entero en lugar de un nombre de variable. El número corresponde al número de variables que uno desea que sean enteros generales. Estas variables deben aparecer primero en la formulación. De tal modo, en este ejemplo sencillo, podríamos haber reemplazado las dos sentencias GIN por la única sentencia GIN 2.
Aplicación mixta de programación con enteros: restricciones "Y-O"
Supongan que una panadería vende ocho variedades de rosquillas. La preparación de las variedades 1, 2 y 3 implica un proceso bastante complicado, por lo que la panadería decidió que no les conviene hornear estas variedades, a menos que pueda hornear y vender por lo menos 10 docenas de las variedades 1, 2 y 3 combinadas. Supongan también que la capacidad de la panadería limita el número total de rosquillas horneadas a 30 docenas, y que la utilidad unitaria de la variedad j es j dólares. Si xj, j = 1, 2, … ,6 denote el número de docenas de la variedad j que se deben hornear, y luego la utilidad máxima puede hallarse resolviendo el siguiente problema (asumiendo que la panadería consigue vender todo lo que hornea):
Maximice Z = S Pj Xj
Sujeta a las restricciones: S Xj £ 30
X1 + X2 + X3 = 0, OR, X1 + X2 + X3 ³ 10
Maximice Z = S Pj Xj
Sujeta a las restricciones: S Xj £ 30
X1 + X2 + X3 - 30y £ 0,
X1 + X2 + X3 - 10y³ 10
Xj ³ 0, y = 0, or 1.
Programas lineales con enteros 0 - 1
Con el comando INT en LINDO se restringe la variable a 0 o 1. A estas variables con frecuencia se las llama variables binarias. En muchas aplicaciones, las variables binarias pueden ser muy útiles en situaciones de todo o nada. Entre los ejemplos podemos incluir cosas tales como asumir un costo fijo, construir una nueva planta o comprar un nivel mínimo de algún recurso para recibir un descuento por cantidad.Ejemplo: Considere el siguiente problema de la mochila
Maximice 11X1 + 9X2 + 8X3 + 15X4
Sujeta a:: 4X1 + 3X2 + 2X3 + 5X4 £ 8, and Xi either 0 or 1.
Con LINDO, la sentencia del problema es:
Max 11X1 + 9X2 + 8X3 + 15X4 S.T. 4X1 + 3X2 + 2X3 + 5X4 £ 8 END INT X1 INT X2 INT X3 INT X4
Luego haga clic en SOLVE. La salida da la solución óptima y el valor óptimo después de ocho iteraciones "Branch-and-Bound" (de rama y frontera).
Observe que en lugar de repetir INT cuatro veces se puede usar INT 4. Las primeras cuatro variables aparecieron en la función objetivo.
VALOR DE LA FUNCION OBJETIVO
1) 24.00000
VARIABLE VALOR COSTO REDUCIDO
X1 0.000000 -11.000000
X2 1.000000 -9.000000
X3 0.000000 -8.000000
X4 1.000000 -15.000000
FILA HOLGURA O EXCEDENTE PRECIOS DUALES
2) 0.000000 0.000000
Nro. DE ITERACIONES = 8
Aplicaciones para formulación de presupuestos de inversiones
Supongan que una compañía de Investigación y Desarrollo dispone de una suma de dinero, D dólares, para invertir. La compañía ha determinado que existen N proyectos en los que conviene invertir, y por lo menos dj dólares deben invertirse en el proyecto j si se decide que ese proyecto j es aquél en el que vale la pena invertir. Asimismo, la compañía determinó que la utilidad neta que puede obtenerse después de invertir en el proyecto j es de jdólares. El dilema de la compañía es que no puede invertir en todos los proyectos N, porqueS dj > D. Por lo tanto, la compañía debe decidir en cuáles de los proyectos invertirá maximizando la utilidad. Para resolver este problema, el asesor formula el siguiente problema:
Xj = 1 si la compañía invierte en el proyecto j, y
Xj = 0 si la compañía no invierte en el proyecto j.
El monto total que se invertirá entonces es de
S dj Xj, y como este monto no puede ser superior a D dólares tenemos la siguiente restricción:
La utilidad total será S Pj Xj. Por lo tanto, la compañía quiere el problema 0-1:
Maximice Z= S Pj Xj
Es un problema de rutina en los hospitales planificar las horas de trabajo de las enfermeras. Un modelo de planificación es un problema de programación con enteros que consiste en minimizar el número total de trabajadores sujeto al número especificado de enfermeras durante cada período del día.
Sujeta a: S dj Xj £ D, Xj = 0, OR 1.
Problemas de scheduling (planificación de turnos)
Si se quiere utilizar la mano de obra lo más eficientemente posible es importante analizar los requerimientos de personal durante las diversas horas del día. Esto es en especial así en las grandes organizaciones de servicios, donde la demanda de los clientes es repetitiva pero cambia de manera significativa según la hora. Por ejemplo, se necesitan muchos más operadores telefónicos durante el período del mediodía a las dos de la tarde que desde la medianoche a las dos de la mañana. Pero, sin embargo, debe haber algunos operadores de guardia durante la madrugada. Como los operadores habitualmente cumplen turnos de ocho horas es posible planificar las horas de trabajo de los operadores de modo tal que un solo turno cubra dos o más "períodos pico" de demanda. Mediante el diseño de planes horarios inteligentes, la productividad de los operadores aumenta y el resultado es un plantel más reducido, y por lo tanto, una reducción en los costos salariales. Algunos otros ejemplos de áreas donde los modelos de scheduling han resultado útiles son los conductores de ómnibus, los controladores de tráfico aéreo y las enfermeras. A continuación analizaremos un problema de ejemplo y desarrollaremos un modelo de programación con enteros para planificar el horario de trabajo de enfermeras.
| Período | Hora del día | Número requerido de enfermeras |
|---|---|---|
| 1 | 8:00 - 10:00 | 10 |
| 2 | 10:00 - 12:00 | 8 |
| 3 | 12:00 - 2:00 | 9 |
| 4 | 2:00 - 4:00 | 11 |
| 5 | 4:00 - 6:00 | 13 |
| 6 | 6:00 - 8:00 | 8 |
| 7 | 8:00 - 10:00 | 5 |
| 8 | 10:00 - 12:00 | 3 |
Como cada enfermera trabaja ocho horas puede comenzar a trabajar al comienzo de cualquiera de los siguientes cinco turnos: 8:00, 10:00, 12:00, 2:00 o 4:00. En esta aplicación no consideramos ningún turno que comience a las 9:00, 11:00, etc. Tampoco es necesario tener enfermeras que comiencen a trabajar después de las 4:00, porque entonces su turno terminaría después de la medianoche, cuando no se necesitan enfermeras. Cada período tiene dos horas de duración, de modo tal que cada enfermera que se presenta a trabajar en el período t también trabajará durante los períodos t + 1, t+ 2, y t + 3 --- ocho horas consecutivas. La pregunta es: "¿Cuántas enfermeras deberían comenzar su turno en cada período para satisfacer los requerimientos del recurso especificados en la tabla anterior?" Para formular el modelo de este problema. Xt es una variable de decisión que denota el número de enfermeras que comenzarán su horario en el período t. La mano de obra total, que deseamos minimizar, es S Xt. Durante el período 1, debe haber por lo menos 10 personas de guardia; entonces, debemos tener X1 ³ 10. De modo similar, los requerimientos del período 2 sólo pueden satisfacerse con X1 + X2 ³ 8. De esta manera denotamos los requerimientos de los períodos restantes:
X1 + X2 + X3 ³ 9,
X1 + X2 + X3 + X4 ³ 11,
X2 + X3 + X4 + X5 ³ 13,
X3 + X4 +X5 ³ 8,
X4 + X5 ³ 5,
X5 ³ 3,
Todas las variables son números enteros.
Observe que X1 no está incluida en la restricción del período 5, ya que las enfermeras que comienzan en el período 1 ya no están en servicio en el período 5. Asimismo, observe que puede resultar necesario tener más que el número requerido de personas en algunos períodos. Por ejemplo, vemos con la primera restricción que el número de enfermeras que comienzan a trabajar en el período 1 debe ser 10, como mínimo. Todas ellas estarán todavía trabajando en el período 2, pero en ese momento sólo se necesitarán ocho personas. Entonces, incluso si X2 = 0,
habrá dos enfermeras extra de guardia en el período 2.
Programación no lineal
La programación lineal ha demostrado ser una herramienta sumamente poderosa, tanto en la modelización de problemas de la vida real como en la teoría matemática de amplia aplicación. Sin embargo, muchos problemas interesantes de optimización son no lineales. El estudio de estos problemas implica una mezcla diversa de álgebra lineal, cálculo multivariado, análisis numérico y técnicas de computación. Entre las áreas especiales importantes se encuentra el diseño de algoritmos de computación (incluidas las técnicas de puntos interiores para programación lineal), la geometría y el análisis de conjuntos convexos y funciones, y el estudio de problemas especialmente estructurados, tales como la programación cuadrática. La optimización no lineal proporciona información fundamental para el análisis matemático, y se usa extensamente en las ciencias aplicadas (en campos tales como el diseño de ingeniería, el análisis de regresión, el control de inventario y en la exploración geofísica).Programación con restricciones no binarias
A través de los años, la comunidad dedicada a la programación con restricciones ha venido prestando considerable atención a la modelística y resolución de problemas usando restricciones unarias y binarias. Ha sido sólo desde hace poco que se viene prestando más atención a las restricciones no binarias, y se debe principalmente a la influencia del número creciente de aplicaciones en la vida real. Una restricción no binaria es una restricción que se define con k variables, donde k normalmente es mayor que 2. En tal sentido, la restricción no binaria puede considerarse como una restricción más global. La modelización de (una parte de) un problema con una restricción no binaria presenta dos ventajas principales: Facilita la expresión del problema y habilita una mayor propagación más poderosa de la restricción a medida que se dispone de información más global.Los éxitos logrados en aplicaciones para programación de itinerarios, horarios de trabajo y rutas han demostrado que usar restricciones no binarias es una dirección de investigación promisoria. De hecho, cada vez más personas creen que este tema es crucial para que la tecnología de las restricciones se convierta en una manera realista de modelizar y resolver problemas de la vida real.
Optimización combinatoria
Agrupar, cubrir y particionar (aplicaciones de los programas con enteros) son los principales temas matemáticos que constituyen la interfaz entre la combinatoria y la optimización. La optimización combinatoria es el estudio de estos problemas. Aborda la clasificación de problemas de programación con enteros, de acuerdo con la complejidad de algoritmos conocidos para resolverlos, y con el diseño de algoritmos apropiados para resolver subclases especiales de problemas. En particular, se estudian problemas de flujos de red, correspondencias y sus generalizaciones matroides. Esta materia es uno de los elementos unificadores de la combinatoria, la optimización, la investigación operacional y la computación científica.Herramientas para el Proceso de Validación de Modelos:
El Lado Oscuro de la Programación Lineal
Introducción:¿Que podría salir mal en el proceso de construcción de un modelo de Programación Lineal (PL)? Los obstáculos potenciales siempre existen, los cuales afectan cualquier aplicación de la PL; Por lo tanto, los tomadores de decisiones y los analistas deben estar concientes de las deficiencias de la PL al momento de crear el modelo.
Los obstáculos potenciales siempre existen, los cuales afectan cualquier aplicación de la PL. Las soluciones óptimas podrían ser no-factibles, ilimitadas, ó podrían existir soluciones múltiples. La degeneración del modelo podría ocurrir. La figura siguiente proporciona una clasificación de para el proceso de validación de modelos de Programación Lineal (PL):
Una Clasificación de Soluciones de Programación Lineal para el Proceso de Validación de Modelos
Characteristics of the Feasible Region (FR)= Características de la Región de Factibilidad (RF.)
Bounded FR = RF Limitada; Empty FR = RF Vacía; Unbounded FR= RF Ilimitada; No Solution= Sin Solución.
Degenerate Solution= Solución Degenerada; Multiple Solution= Soluciones Multiples; Unbounded Solution= Solución Ilimitada; Unique Solution= Solución Unica; Bounded Solution= Solución Limitada.
Estos y otros obstáculos no son mucho más de las deficiencias en la programación lineal pero son situaciones de las cuales los tomadores de decisiones deberían estar conscientes. ¿Que podría salir mal en el proceso de construcción de un modelo de Programación Lineal (PL)?
Problemas con los Paquetes de PL: La mayoría de los software para resolver problemas de PL tienen problemas en reconocer el lado oscuro de la PL, y/o dar alguna sugerencia ó remedio para resolverlo. Resuelva el problema siguiente utilizando el WinQSB, y luego descubra y reporte los resultados obtenidos.
Ilimitación
Identificación: En el Algoritmo Simplex, si se introduce una columna j y todos los aij en esa columna son menores o iguales a cero, el ratio la columna (C/R) no puede ser determinado. Vea también el caso de degeneración.Por ejemplo, considere el siguiente problema:
Max Y1
sujeto a:
Y1 + Y2 -2T = 0
Y1 -Y2 = 2
todas la variables de decisión son ³ 0.
A continuación por ejemplo, en el método libre-artificial, obtenemos la tabla siguiente:
| BVS | Y1 | Y2 | T | LMD | |
|---|---|---|---|---|---|
| T | 0 | -1 | 1 | 1 | |
| Y1 | 1 | -1 | 0 | 2 | |
| Cj | 0 | 1 |
A pesar de que la variable Y2 debería entrar como una variable básica, todos los elementos en esta columna son menores que cero, Por lo tanto, el problema de programación lineal es ilimitado.
Aprenda que una solución óptima ilimitada significa tener una región de factibilidad cerrada ilimitada, sin embrago, la situación inversa de este enunciado podría no ocurrir. Una solución óptima ilimitada significa que las restricciones no limitan a la solución óptima y que la región de factibilidad se extiende hasta el infinito.
Resolución: En la vida real, esta situación es muy extraña. Revise la formulación de las restricciones, faltan una o más restricciones. Revise también alguna mala especificación de las restricciones en cuanto a las direcciones de las inigualdades o errores numéricos.
El Análisis de Sensibilidad no es aplicable.
Los software WinQSB y Lindo establecen que el problema es ilimitado.
Región de Factibilidad Ilimitada: Tal y como se mencionó anteriormente, aprenda que una solución ilimitada requiere una región de factibilidad cerrada ilimitada. La situación inversa de este enunciado podría no ocurrir. Por ejemplo, el siguiente problema de PL tiene una región de factibilidad cerrada ilimitada, sin embargo, la solución es limitada:
Max -4X1 -2X2
sujeto a:
X1 ³ 4
X2 £ 2
todas las variables de decisión son ³ 0.
La solución óptima es X1 = 4, y X2 = 0.
Soluciones Optimas Múltiples (soluciones óptimas Innumerables)
Identificación: En la tabla de iteración final del Simplex, si la fila Cj (la última fila en la tabla) es cero para una o más de las variables no-básicas, tendríamos dos soluciones óptimas (por lo tanto muchas infinitas) Para encontrar la otra esquina ( si existe), se hace un pivote en una columna no–básica con Cj igual a cero.La condición necesaria para que exista un PL con múltiples soluciones: Si el número total de ceros en el Costo Reducido junto al número de ceros la columna de Precio Sombra exceden el número de restricciones, se podrían tener múltiples soluciones. Si se realiza una corrida del problema anterior en un software como WinQSB ó Lindo, se encontrarán cuatro ceros. Sin embargo, debe darse cuenta que esta es simplemente una condición Necesaria y no una condición Suficiente, así como en el ejemplo numérico anterior. Desafortunadamente, el QSB utiliza esta condición necesaria. Por lo tanto, proporciona mensajes Erróneos.
Ejemplo: El problema siguiente tiene varias soluciones:
Max 6X1 + 4X2
sujeto a:
X1 + 2X2 £ 16
3X1 + 2X2 £ 24
todas las variables de decisión son ³ 0.
Utilizando el software QSB, usted obtendrá dos soluciones, (X1 = 8, X2 = 0) y (X1 = 4, X2 = 6). Note que, la existencia de soluciones múltiples significa que tenemos soluciones óptimas innumerables (No solo dos).
Siempre que existan dos vértices que sean óptimos, se pueden generar todas las otras soluciones óptimas mediante la "combinación lineal " de las coordenadas de las dos soluciones. Por ejemplo, para el ejemplo anterior basado en dos soluciones obtenidas del QSB, todas las soluciones siguientes son por lo tanto óptimas:
X1 = 8a + (1 - a)4 = 4 + 4a, X2 = 0a + (1- a)6 = 6 - a, para todos los 0 £ a £ 1.
Resolución: Revise los coeficientes dela función objetivo y las restricciones. Podrían existir errores de aproximación ó redondeo.
Análisis de Sensibilidad No aplicable.
El WinQSB y Lindo sostienen que el problema es ilimitado.
Análisis de Sensibilidad: El análisis de sensibilidad se basado en una solución óptima podría no ser válida para las demás.
Advertencia al Usar Paquetes de Software: Desafortunadamente, Lindo, no proporciona ninguna advertencia directa sobre la existencia de soluciones múltiple. El WinQSB indica que una solución óptima alternativa ha sido encontrada. Sin embargo, este tipo de enunciado podría ser confuso. Por ejemplo, el problema siguiente tiene una única solución óptima, cuando el WinQSB indica la existencia de múltiples soluciones.
Max 30X1 - 4X2
Sujeto a:
5X1 - X2 £ 30
X1 £ 5
X1 ³ 0
X2 is unrestricted.
La única solución es X1 = 5, X2 = -5 con un valor óptimo de 170.
Para el problema siguiente, el WinQSB proporciona 4 soluciones múltiples distintas:
Minimizar X1 + X2 + 2X3
Sujeto a:
X1 + X2 + X3 ³ 10
X1 + X2 + 2X3 ³ 13
X1, X2 son no-negativas.
El conjunto de soluciones óptimas para este problema constituye la mitad del plano. Es decir, todas las soluciones óptimas se encuentran en el plano X1 + X2 + 2X3 = 13, tal que X1 + X2 + X3 ³ 10, X1 ³ 0, X2 ³ 1, y X3 ³ 0.
No Soluciones (PL No-Factible)
Una solución no-factible significa que las restricciones son demasiado limitantes y no han dejado espacio para la región de factibilidad.El problema siguiente por ejemplo, no tiene solución:
Max 5X1 + 3X2
sujeto A:
4X1 + 2X2 £ 8
X1 ³ 4
X2 ³ 6.
Identificación: Si no se puede traer ninguna variable mientras se mantiene la factibilidad (es decir, los valores de LMD restantes son no-negativos).
Resolución: Revise las restricciones por cualquier mala especificación en las direcciones de las inigualdades, y por errores numéricos. Si no existen errores, entonces existen conflictos de intereses. Esto puede ser resuelto encontrando el IIS (vea la Nota de abajo) y luego reformule el modelo.
Análisis de Sensibilidad: No aplicable.
Note: La mayoría de los software comerciales tales como CPLEX y LINDO tienen una función llamada IIS (Irreducible Infeasible Subset= Subconjunto de Infactibilidad Reducible) es decir, el conjunto de restricciones mínimas necesarias a remover del problema de forma tal de hacerlo factible. Este conjunto de restricciones es no-factible, pero un subconjunto apropiado de un IIS es factible. Por lo tanto todas las restricciones en el IIS contribuyen a la no-factibilidad. Esto significa que se puede remover o modificar por lo menos una de las restricciones en la IIS de forma tal de proporcionar factibilidad al modelo. Por lo tanto, encontrar una IIS simplemente ayuda a enfocar los esfuerzos en el diagnóstico. Podrían existir varias IIS en el modelo y un simple error se podría presentar en diferentes formas de IIS. En consecuencia, se debe reparar el modelo de la forma siguiente:
Paso 1: encontrar una IIS,
Paso 2: reparar la infactibilidad en la IIS, y
Paso 3: revisar si el modelo es su totalidad es ahora factible, si no, realice el paso de nuevo.
En los Paquetes de Generación de Horarios, por ejemplo, la eliminación total de inconsistencias en los datos iniciales es una tarea ardua. Por lo tanto, algunos paquetes están equipados con un módulo de interfaz que actúa como un depurador. Esto eliminará mucho de los problemas de infactibilidad durante el nivel superficial de la primera corrida. Como un acercamiento alternativo, los problemas de infactibilidad pueden ser manejados como un problema de optimización lineal, con el objetivo de minimizar el número de violaciones de restricciones (posiblemente ponderadas.) Cuando ninguna solución satisface todas las restricciones, una solución cercana es encontrada. Esta solución cercana podría resaltar los datos de entrada que generan conflicto a los cuales se debe dirigir.
Degeneración
Un vértice degenerado es uno a través del cual pasan mas de n hiper- planos si estamos en el n-ésimo espacio Euclideano, digamos 3 líneas en un espacio de 2 dimensiones. En dicho vértice un método como el Simplex puede cambiar de una representación (con n hiper-planos) a otra, y podría terminar de forma cíclica en el primero y luego repeir este “ciclo”. Ahora, agregando pequeñas cantidades para (digamos, el LMD de las restricciones) mover ligeramente al hiper-plano correspondiente y “perturbar” el vértice. En vez, existirán muchos vértices cercanos donde solo hiper-planos se encuentran. Ahora, el método puede ir de uno a otro (mejorando cada vez la función objetivo) y dejar esta área de degeneración. Luego, la perturbación puede ser apagada de nuevo en implementaciones computacionales modernas del método Simplex y sus muchas variaciones.Un punto de esquina (vértice) en un problema de variables de decisión n- dimensional es llamado vértice de degeneración si más de n restricciones se hacen activas (relevantes a la solución) en el punto de esquina. Esto es siempre que un punto de esquina se oscula. Por ejemplo, en un problema de 2 dimensiones, un punto de esquina es degenerado si en el 3 o mas restricciones se convierten en igualdades.
Por ejemplo, considere el siguiente problema de dos dimensiones:
Max X1 + X2
sujeto a:
X1 £ 1
X2 £ 1
X1 + X2 £ 2
todas las variables de decisión son ³ 0.
La solución óptima es X1 = 1, y X2 = 1, en el cual todas las tres restricciones son activas.
Siempre que la solución óptima sea degenerada, se obtendrán múltiples precios sombra. Para el problema anterior, los dos grupos de precios sombra son (1, 1, 0) y (0, 0, 1) como se podría verificar si se construye y soluciona el problema dual
Identificación: Si existen por lo menos dos ratios de columna mas pequeños e iguales (bi/aij) mientras se aplica el método Simplex, la solución es degenerada y arbitrariamente escoge una variable saliente.
En casos extraños, la degeneración podría causar ciclismos, así como se muestra en el problema siguiente::
Max 6X1 + 3X2
sujeto a:
X1 £ 1
X2 £ 1
X1 - X2 £ 1
-X1 + X2 £ 1
todas las variables de decisión son ³ 0.
Ambos, el Lindo y el WinQSB toman 3 iteraciones para resolver este problema simple de degeneración.
Resolución: agregue al valor de LMD un número pequeño, como 0,001. Esto debería resolver el problema.
Análisis de Sensibilidad: El análisis de sensibilidad podría ser IN- valido y usted podría tener Precios Sombra Alternativos.
El problema siguiente y su dual son ambos degenerados:
Min X2
sujeto a:
X2 - 2X3 + X4 = 1
X1 + 2X2 - X3 = 0
X1 + X2 + 3X3 = 2
todas las variables de decisión son ³ 0.
Redundancia Entre las Restricciones
Redundancia significa que algunas de las restricciones no son necesarias dado que existen otras mas severas. Para un caso sencillo de PL con restricciones redundantes, considere el siguiente ejemplo numérico:Maximice 5X1 + 6X2
sujeto a: 3X1 + 6X2 £ 8, 6X1 + 4X2 £ 24, and both X1, X2 ³ 0.
Identificación: Por lo menos una fila en la tabla de iteración tiene todos los elementos incluyendo los de LMD con valores iguales a cero.
Resolución: Elimine dicha fila y prosiga. Sin embargo, la redundancia en las restricciones no es absoluta sino relativa. Adicionalmente, lo “minimalista” de un conjunto de restricciones, es decir, que no existen redundantes para describir una región de factibilidad, no implica necesariamente que el número de restricciones es el mas pequeño.
Análisis de Sensibilidad: El análisis de sensibilidad de LMD podría ser invalido por que las restricciones redundantes no están disponibles, adicionalmente se podrían tener Precios Sombra Alternativos. Por ejemplo, en casi todos los Modelos de Redes una de las restricciones es siempre redundante, por lo tanto los resultados del análisis de sensibilidad de paquetes de computadora (tales como el modulo de QSB) para este tipo de problemas podrían ser inválidos.
PL sin Vértices
La PL siguiente no posee vértices:Maximice X1 + X2
sujeto a: X1 + X2 £ 5, X1, X2 sin restricción.
Este problema tiene una región de factibilidad cerrada sin restricción y sin vértices. Sin embargo, todas las soluciones múltiples son los puntos sobre la línea X1 + X2 = 5.
La Forma Estándar: Mediante la conversión de las inigualdades en igualdades con una variable de rezago S1, y restringiendo las variables por X1 - y, y X2 -y, encontramos la siguiente solución básica:
| X1 | X2 | y | S1 | X1+X2 | |
| __________________________ | |||||
| 0 | 0 | 0 | -5 | no- factible | |
| 0 | 0 | -5/2 | 0 | no- factible | |
| 0 | 5 | 0 | 0 | 5 | |
| 5 | 0 | 0 | 0 | 5 | |
Esto proporciona dos soluciones básicas simples con valores objetivos iguales. Esto indica que, existen soluciones múltiples, sin embargo, la región de factibilidad original se encuentra distorsionada!
Para este problema, el WinQSB proporciona dos soluciones óptimas distintas: (X1 = 5, X2 = 0), y (X1 = 0, X2 = 5) las cuales no son vértices. Esto significa que, no solo cualquier combinación convexa de estos dos puntos es óptima, sino que los puntos mas allá de ellos son por lo tanto óptimos.
PL con Soluciones Optimas Ilimitadas y de Restricción Múltiple
Considere el siguiente problema de PL:Maximice X1 + X2
sujeto a: X1 + X2 = 5, ambos X1, y X2 son no-restringidos en signo.
Este problema tiene una región de factibilidad cerrada e ilimitada. Existen soluciones óptimas múltiples, tanto limitadas como ilimitadas, las cuales son los puntos sobre la línea X1 + X2 = 5.
Sobre Las Variables de Decisión Básicas y no-Básicas
Cuando se realizan las iteraciones del Simplex, se cumple que “cuando una variable de decisión se hace una variable básica, esta se mantiene básica”. Pues no!, no siempre es así. Una variable de decisión no-básica puede convertirse básica durante las iteraciones del Simplex, y en una iteración siguiente convertirse no-básica de nuevo. Considere el problema siguiente:
Maximice 5X1 + 6X2
sujeto: 3X1 + 6X2 £ 8, 6X1 + 4X2 £ 24, y ambos X1, X2 ³ 0.
Aplicando el método Simplex para resolver el problema, la variable de decisión X2 se hace básica luego de la primera iteración. Sin embargo, en la segunda iteración, la variable de decisión X1 reemplaza a X2 como nueva variable básica. En la segunda iteración para este problema, proporciona también la solución óptima. Note que, una de las restricciones es redundante.
PL sin Ninguna Solución Interior
Considere el problema siguiente:Maximice X1 + 2X2
sujeto a: X1 + X2 = 2, X1 ³ 0, X2³ 0.
Este problema no tiene puntos interiores. Un punto interior es un punto de factibilidad, dado que usted dibuja un pequeño círculo alrededor de ese punto, y por lo tanto todos los puntos dentro del círculo son también factibles. No existen puntos factibles con tales propiedades. Consecuentemente, este problema posee un conjunto interior vacío. Sin embargo, el problema tiene dos vértices en: (2, 0), y (0, 2) de donde el segundo es la solución óptima con valor óptimo de 4.
PL sin Ninguna Solución Interior ni Solución Acotada
Considere el problema siguiente:Maximice X1 + 2X2
sujeto a: X1 + X2 = 2, X1 - X2 = 0, X1³ 0, y X2 ³ 0.
El problema tiene una región de factibilidad la cual es el punto simple (X1 = 1, X2 = 1), con un valor óptimo de 3. Por lo tanto, este problema no tiene punto interior ni punto limitado (acotado). Solo posee un vértice.
PL con un Punto Interior como Optimo
Considere el problema siguiente:Maximice X1 + X2 + X3 + X4
sujeto a: X1 + X2 = 100, X1 + X3 = 150, X3 + X4 = 200, todas las Xi ³ 0.
Por ejemplo, la solución ótima X1 = 50, X2 = 50, X3 = 100, X4 = 100, con valor óptimo de 300, es un punto interior de la región de factibilidad para este problema. De hecho, cualquier solución factible (no necesariamente básica) es una solución óptima también.
Para algunas situaciones adicionales interesantes, viste el sitio Web Mitos y Contraejemplos en la PL
Solución Optima Generada por un Paquete de PL no es la Misma Obtenida por Otro Paquete
La Solución obtenida por paquete de PL podría no ser la misma que se obtendría con otro paquete. Considere el siguiente ejemplo numérico:
Minimice X1 + X2 + 2X3
Sujeto a:
X1 + X2 + X3 ³ 10
X1 + X2 + 2X3 ³ 13
X1, X2 sin restricción en el signo
WinQSB: Utilizando el paquete de WinQSB, se encontrarán las soluciones múltiples siguientes: A = (0, 7, 3) y B = (7, 0, 3). Esto sugiere que todos los puntos entre estas soluciones óptimas generadas son también óptimas. Todas las combinaciones lineales de estas dos soluciones son también óptimas:
X1 = 0a + (1 - a)7 = 7 - 7a,
X2 = 7a + (1- a)0 = 7a,
X3 = 3a + (1- a)3 = 3,
para todo 0 £ a £ 1.
Sin embargo, note que ambas restricciones son activas, por lo tanto las soluciones se encuentran sobre la intercepción de estos dos planos, el cual es una línea. Adicionalmente, cualquier punto sobre la línea no esta restringido a los a estar entre los puntos A y B. En otras palabras, es cualquier punto sobre la línea de intercepción (en forma paramétrica):
X1 = t,
X2 = 7 - t,
X3 = 3,
son óptimos, para todo t, inclusive cuado t es una M-grande.
Por lo tanto, este problema de PL no tiene vértices, tiene multiples soluciones limitadas, y soluciones ilimitadas.
Lindo: Para correr este problema en Lindo, primero se debe satisfacer las condiciones de no-negatividad mediante la sustitución de para cada variable no-restringida Xi = xi - y. El resultado es:
min x1 + x2 + 2x3 - 5y
sujeto a:
x1 + x2 + x3 - 3y ³ 10
x1 + x2 + 2x3 - 5y ³ 13
Todas las variables son no-negativas.
Corriendo este problema en Lindo (o su WinQSB), se obtiene x1 = 13 y todas las demás variables son iguales a cero. En términos de las variables originales, se obtiene: X1= 13, X2 = 0, y X3 = 0. Como se puede observar, la solución obtenido por Lindo no es obtenible por WinQSB y viceversa. Obviamente, los resultados de sensibilidad para este problema utilizando cualquiera de estos paquetes no son validos. El conjunto de todas las soluciones óptimas es un medio plano, es decir:
Max 10U1 + 13U2
Sujeto a:
U1 + U2=1
U1 + U2=1
U1+2U2=2
Todas las variables son no-negativas.
Corriendo el problema dual en Lindo (o en su WinQSB), obtenemos U1 = 0, U2 = 1, con precios sombra de (0, 13, 0) los cuales son la solución para el primal obtenidos previamente por el Lindo (o WinQSB). Sin embargo, eliminando la primera restricción redundante en el problema dual, tenemos :
Max 10U1 + 13U2
Sujeto a:
U1 + U2=1
U1+2U2=2
Todas las variables son no-negativas.
Ahora, haciendo la corrida en el Lindo (o WinQSB), obtenemos U1 = 0, U2 = 1, con los precios sombra de (7, 3) los cuales son las soluciones del primal (0, 7, 3) obtenidas previamente por el WinQSB. La otra solución es no producible.
Utilizando el WinQSB para el problema dual, obtenemos U1 = 0, U2 = 1, con los precios sombra de (0, 7, 3) el cual es una de las soluciones del primal obtenidas previamente mediante este software.
¿La Tabla Optima del Simplex Proporciona una Solución Dual?
La utilidad de la tabla del simplex para aplicaciones gerenciales es obtenida por el hecho de que esta contiene toda la información necesaria para realizar análisis de sensibilidad, asi como usted aprenderá posteriormente en este curso. Sin embargo, la tabla óptima del simplex no proporciona la solución dual por si mismo. Los precios sombra son las soluciones del problema dual.Como usted ahora sabrá, los precios sombra pueden ser positivos, cero o igualmente negativos, sin embargo, en la tabla final del simplex la última fila debe ser siempre no-positiva (así como lo requiere los algoritmos de solución). Por lo tanto, no podemos simplemente leer los valores de los precios sombra en la tabla final sin antes formular el problema dual.
Ejemplo Numérico: Considere problema siguiente,
Maximice 3X1 + 5X2
Sujeto a:
X1 + 2X2 £ 50,
-X1 + X2 ³ 10,
X1 ³ 0, X2 ³ 0.
Introduciendo variables de exceso y defecto S1 y S2 respectivamente, y siguiendo los pasos de la Solución Algorítmica Libre-Artificial, obtenemos la tabla final de simplex siguiente:
| BVS | X1 | X2 | S1 | S2 | LMD | |
|---|---|---|---|---|---|---|
| X1 | 1 | 0 | 1/3 | 2/3 | 10 | |
| X2 | 0 | 1 | 1/3 | -1/3 | 20 | |
| Cj | 0 | 0 | 8/3 | 1/3 |
Los precios sombra no son (8/3, 1/3). Como usted observa, después de construir el problema dual, el cual es:
Minimice 50Y1 + 10Y2
Sujeto a:
Y1 - Y2 ³ 3,
2Y1 + Y2 ³ 5,
Y1 ³ 0,
and Y2 £ 0.
Obteniendo la formulación del problema dual, ahora se pueden leer correctamente los precios sombra. Por lo tanto, los precios sombra son Y1 = 8/3, y Y2 = -1/3. De nuevo, cuando se construye el dual del problema se observa que Y2 tiene que ser £ 0, en signo. Esta es la razón por la cual se toma -1/3 en vez de 1/3 para Y2, de la tabla final del simplex.
La Conversión a la Forma Estándar Podría Distorsionar la Región de Factibilidad
Considere el siguiente problema de PL:Maximice X1 + X2
sujeto a: X1 + X2 £ 5, X1, X2 no-restringido.
Este problema tiene una región de factibilidad cerrada ilimitada sin vértices. Sin embargo, todas las soluciones múltiples son los puntos sobre la línea X1 + X2 = 5.
Ahora veamos que obtenemos si convertimos este problema a forma estándar, el cual es un requerimiento para iniciar el Método Simplex.
La Forma Estándar: Convirtiendo las inigualdades en igualdades con la variable de exceso S1 y restringiendo las variables mediante X1 - y, y X2 -y, obtenemos la forma estándar siguiente:
Maximice X1 + X2 -2y
sujeto a:
X1 + X2 -2y + S1 = 5, y todas las variables están restringidas en signo.
Las soluciones básicas son:
| X1 | X2 | y | S1 | X1+X2 | |
| _________________________ | |||||
| 0 | 0 | 0 | 5 | 0 | |
| 0 | 0 | -5/2 | 0 | no-factible | |
| 0 | 5 | 0 | 0 | 5 | |
| 5 | 0 | 0 | 0 | 5 | |
Esto proporciona vértices óptimos. Esto indica que existen soluciones múltiples. Sin embargo, la región de factibilidad original se encuentra ahora distorsionada!, esto significa que no somos capaces de producir todas las soluciones mediante el uso de cualquier combinación convexa de las dos soluciones (0, 5) y (5, 0).
Para encontrar la solución a este problema, se necesitan saber las dos definiciones siguientes:
Raya: Una raya es la mitad de una línea: {V + ah: a ³ 0}, de donde h es un vector no-cero contenido en S. El punto V es llamada la raíz, por lo tanto se dice que la raya esta enraizada a V.
Raya Extrema: Una raya extrema de un conjunto cerrado de S es una raya que no puede ser expresada como combinación lineal de cualquier otra raya de S.
Todos los puntos óptimos están localizados en cualquiera de los dos extremos de la raya ambos arraizados a V = (0, 5), en las direcciones (1, -1), y (-1, 1):
(X1, X2) = (0, 5) + a1(1, -1) + a2(-1, 1) =
(a1 - a2, 5 - a1 + a2),
para todo a1 ³ 0, y a2 ³ 0.
En vez de (0, 5) cualquier punto sobre la línea puede ser utilizado.
Sin embargo, para representar todos los puntos en la región de factibilidad, se necesita un término adicional:
(X1, X2) = (0, 5) + a1(-1,1) + a2(1,-1) + a3(-1,-1),
para todo a1 ³ 0, a2 ³ 0, y a3 ³ 0.
El último término necesario para todos los puntos por debajo de la línea. Esto se obtiene del hecho de que ambas variables son no-restringidas en signo [en direcciones [(0, -1) y (-1, 0)].
La idea general para la representación paramétrica es que comenzamos en el vértice. Nos movemos es la dirección de factibilidad de cada borde al próximo punto factible. Si dicho punto existe (es decir, hemos encontrado oto vértice). Si no, el poliedro no es restringido en esa dirección, lo que significa que dicha dirección es una raya extrema. Note que, un poliedro sin vértices siempre contiene una línea (o hiper-plano). Para dicho poliedro adicionamos una raya perpendicular a la línea (o hiper-plano) si la restricción tiene la forma de inigualdad ( ³, o £ como en el ejemplo anterior.
Remover las Restricciones de Igualdad Mediante la Sustitución Podría Cambiar el Problema:
Siempre que exista cualquier restricción en forma de igualdad en u problema de PL, existe la tentación de reducir el tamaño del problema removiendo las restricciones de igualdad mediante la sustitución. El problema se mantiene igual si se eliminan la(s) variable(s) no-restringidas mediante la igualdad de restricciones (si es posible). Sin embargo, si no existen variables no-restringidas, se debe remover la restricción de igualdad mediante la sustitución dado que esto podría generar otro problema de PL totalmente diferente. Este es un ejemplo para remover una restricción de igualdad:Max X1
Sujeto a:
X2 + X3 = -1
X1 - 2X2 + X3 £ 1
X1 + X2 £ 2
Todas las variables son no-negativas.
Este problema no tiene solución. Sin embargo, sustituyendo, digamos X3 = -1 - X2 en todos lados, el problema cambia a:
Max X1
Sujeto a:
X1 - 3X2 £ 2
X1 + X2 £ 2
Todas las variables son no-negativas,
Obteniendo una solución óptima de (X1 = 2, X2 = 0), con un valor óptimo de 2. por lo tanto, estos dos problemas No son equivalentes.
Sin embargo, usted se preguntará: ¿Bajo que condiciones es seguro el eliminar una restricción de igualdad por sustitución? La respuesta es, ya sea bajo una variable no-restringida, como se mencionó anteriormente, o si todos los coeficientes de una restricción de igualdad tiene el mismo signo que LD, entonces sería seguro el eliminar cualquier variable por sustitución de forma tal de reducir el número de variables y restricciones.
Interpretación Errónea del Precio Sombra
El Precio Sombra nos dice en cuanto la función objetivo cambiará si cambiamos el lado derecho (LMD) de la restricción correspondiente. Esto es llamado comúnmente el “valor marginal”, “precio dual” o “valor dual” para la restricción. Por lo tanto, el precio sombra no seria el mismo que el “precio de Mercado”.Para cada LMD de las restricciones, el Precio Sombra dice exactamente en cuanto cambiará la función objetivo si cambiamos el lado derecho (LMD) de la restricción correspondiente dentro de los límites dados en el rango de sensibilidad del LMD.
Por lo tanto, para cada valor de LMD, el precio sombra es el ratio del cambio en el valor óptimo causado por cada incremento (descenso) permitido dentro del cambio permisible del LMD.

Un Contraejemplo:
Considere la siguiente PL:
Max X2
sujeto a:
X1 + X2 £ 2
2,5X1 + 4X2 £ 10
donde ambas variables de decisión son no-negativas.
Este problema logra su solución óptima en (0, 2) con un valor óptimo de 2.
Suponga que se desea calcular el precio sombra del primer recurso, lo cual es la LMD de la primera restriccón.
Cambiando la LMD de la primera restricción incrementándolo en una unidad, obtenemos:
Max X2
Sujeto a:
X1 + X2 £ 3
2,5X1 + 4X2 £ 10
Donde ambas variables de decisión son no-negativas.
El nuevo problema tiene una solución óptima de (0, 2,5) con un valor óptimo de 2,5.
Por lo tanto, esto parece “como si” el precio sombra para este recurso es 2,5 - 2 = 0,5. De hecho el precio sombra para este recurso es 1, el cual puede ser encontrado mediante la construcción y resolución del problema dual.
La razón para este problema se hace evidente si se nota que la tolerancia incrementa para mantener la validez de que el precio sombra del primer recurso es 0,5. El incremento en 1 esta mas allá del cambio permitido en el primer valor del LMD.
Suponga ahora que cambiamos el mismo valor de LMD por + 0,1 el cual es permisible, luego el valor óptimo para el nuevo problema es 2,1. Por lo tanto el precio sombra es (2,1 -2) / 0,1 = 1. Debemos ser cuidadosos cuando calculamos el precio sombra.
Si desea calcular el precio sombra de un LMD cuando su rango de sensibilidad no es disponible, usted lo podría obtener para por lo menos dos perturbaciones. Si la tasa de cambio para ambos casos le proporciona los mismos valores, esta tasa es por lo tanto el precio sombra. Como un ejemplo, suponga que perturbamos el LMD de la primera restricción por +0,02 y –0,01. Resolviendo el problema después de estos cambios utilizando su software para resolver su PL, los valores óptimos son 2,02, y 1,09, respectivamente. Dado que el valor óptimo para el problema nominal (sin ninguna perturbación) es igual a 2, la tasa de cambio para estos dos casos son: (2,02 - 2)/0,02 = 1, y (1,09 - 2)/(-0,01) = 1, respectivamente. Dado que estas dos tasa son la misma, concluimos que el precio sombra para la LMD de la primera restricción es por lo tanto igual a 1.
¿Es el Precio Sombra Siempre no-Negativo?
Usted podría preguntarse “¿Es el precio sombra de un valor de LMD siempre no-negativo?” Esto solo depende de la formulación del primal y su dual. Lo que es importante para recordar es que el precio sombra de un LMD dado es la tasa de cambio en el valor óptimo con respecto a ese LMD, dado que el cambio se encuentra dentro de los límites de sensibilidad de ese LMD.Considere el siguiente ejemplo numérico:
Max 3X1 + 5X2
Sujeto a:
X1 + 2X2 £ 50
-X1 + X2 ³ 10
X1, X2 son no-negativos.
Estamos interesados en encontrar el precio sombra de LMD2 = 10. el problema dual es:
Min 50U1 + 10U2
Sujeto a:
U1 - U2 ³ 3
2U1 + U2 £ 5
U1 ³ 0, mientras que U2 £ 0
Esto se puede verificar utilizando el software WinQSB. La solución para el dual es U1 = 8/3, U2 = -1/3. Por lo tanto, el precio sombra para el LMD2 = 10 es U2 = -1/3. Esto significa que por cada unidad de incremento (descenso) en el valor de LMD2 el valor óptimo para el problema primal decrece (incrementa) en 1/3, dado el cambio en que el LMD2 se encuentra entre sus límites de sensibilidad.
Para otro ejemplo del mismo problema primal, note que el problema puede ser escrito de forma equivalente mediante el cambio en la dirección de la segunda restricción de inigualdad:
Max 3X1 + 5X2
Sujeto a:
X1 + 2X2 £ 50
X1 - X2 £ -10
X1, X2 son no-negativos.
El problema dual para este problema primal ahora es ahora:
Min 50Y1 - 10Y2
Sujeto a:
Y1 + Y2 ³ 3
2Y1- Y2 £ 5
Ambos Y1 y Y2 son no-negativos.
De nuevo, la formulación del dual puede ser verificada utilizando el software WinQSB software. La solución a este problema dual es Y1 = 8/3 y Y2 = 1/3. Por lo tanto, el precio sombra para LMD2 = -10 es Y2 = 1/3. esto significa que para cada unidad de incremento (descenso) en el valor LMD2, el valor óptimo para el problema primal incrementa (decrece) en 1/3, dado que el cambio en LMD2 se encuentra dentro de los límites de sensibilidad.
Como usted previamente notó, ambos problemas duales son el mismo cuando se sustituye U1 = Y1, y U2 = -Y2. Esto significa que los precios sombra obtenidos por el LMD2 = 10, y LMD2 = -10 tienen el mismo valor con signos contrarios (como se esperaba). Por lo tanto, el signo del precio sombra depende de cuando se formula el problema dual, a pesar de que su significado e interpretación son siempre los mismos.
Visite adicionalmente
Situaciones de Mas-por-Menos & Menos-por-Mas.
Precios Sombra Alternativos
Suponga que tenemos una PL y esta tiene una solución óptima única. ¿Es posible encontrar mas de un conjunto de precios duales?Si, es posible. Considere el problema siguiente:
Min 16X1 + 24X2
sujeto a:
X1 + 3X2 ³ 6
2X1 + 2X2 ³ 4
todas las variables de decisión son ³ 0.
Su solución dual es:
Max 6U1 + 4U2
sujeto a:
U1 + 2U2 £ 16
3U1 + 2U2 £ 24
todas las variables de decisión son ³ 0,
Este problema dual tiene varias soluciones alternativas tales como, (U1 = 8, U2 = 0) y (U1 = 4, U2 = 6). Todas las combinaciones convexas de estos dos vértices son soluciones también.
Existen casos generales para los cuales los precios sombra no son únicos. Así como en el ejemplo anterior, siempre que exista redundancia entre las restricciones, o si la solución óptima es “degenerada”, debería existir masa de un conjunto de precios duales. En general, la interdependencia lineal de las restricciones son una condición suficiente para la unicidad de los precios sombra.
Considere el siguiente problema de PL con restricciones redundantes:
Max 10X1 + 13X2
Sujeto a:
X1 + X2 = 1
X1 + X2 = 1
X1+ 2X2 = 2
y todas las variables son no-negativas.
Haciendo la corrida del dual en Lindo (o su WinQSB ) se obtiene el resultado en X1 = 0, X2 = 1, con los precios sombra de (0, 13, 0).
Usando el WinQSB para este problema, obtenemos X1 = 0, X2 = 1 con diferentes precios sombra de (0, 7, 3).
En el caso de redundancia, el precio sombra obtenido por un paquete de PL podría no ser el mismo obtenido por otro.
Situaciones de Mas-por Menos & Menos-por Mas
Considere el siguiente problema de PL de producción:
Maximizar X1 + 3X2 + 2X3
sujeto a: X1 + 2X2 + X3 = 4, 3X1 + X2 + 2X3 = 9, todos los Xi son no-negativos.
El total e horas de trabajo son 4 y 9. El valor óptimo para este problema es $7.
Ahora, si se cambia la segunda disponibilidad de trabajo desde 9 a 12, el valor óptimo sería $4. Esto significa que se ha trabajado mas horas por menos ingreso.
Esta situación se encuentra con frecuencia y es conocida como “La Paradoja de Mas-por Menos”. El recurso número 2 tiene un precio sombra negativo!
Para determinar el mejor número de horas, se debe trabajar para maximizar el ingreso mediante la resolución de la siguiente PL paramétrica:
Maximice X1 + 3X2 + 2X3
sujeto a: X1 + 2X2 + X3 = 4, 3X1 + X2 + 2X3 = L , L, y todos los Xi son no-negativos.
Usando LINDO ( su WinQSB) debemos resolver
Maximice X1 + 3X2 + 2X3
sujeto a: X1 + 2X2 + X3 = 4, 3X1 + X2 + 2X3 - L = 0.
El L óptimo es 8 horas, y el valor óptimo es $8!
La condición necesaria y suficiente para la situación de existencia de mas-por-menos/ menos- por –mas es tener restricción (es) de igualdad con precio (s) sombra negativo (s) para los valores de LMD.
Declaración de derechos de propiedad intelectual: El uso legítimo, según las pautas de 1996
guías de consulta justas del uso para los multimedia educativos,
de los materiales presentados en este sitio Web está permitido para propósitos educativos no comerciales.
Este sitio puede duplicarse, intacto con esta
declaración, en cualquier servidor de acceso público y puede vincularse a cualquier otra página Web. Todos los archivos se encuentran disponibles en
http://home.ubalt.edu/ntsbarsh/Business-stat para el duplicado.
Agradecería recibir comentarios, sugerencias e inquietudes por e-mail. Gracias.