Herramientas para el Análisis de Decisión:
Análisis de Decisiones Riesgosas

Sitio Espejo para América Latina
Sitio en los E.E.U.U.

Esta es la versión en Español del sitio Web principal en Inglés, el cual se encuentra disponible en:
Probabilistic Modeling Process: Decision Analysis

USA Site

Este sitio muestra el proceso de análisis de alternativas para la toma de decisiones publicas y privadas, usando diferentes criterios de decisión, diferentes tipos de información e información de calidad variable. Describe los elementos usados en el análisis de las alternativas de decisión y elección, así como también las metas y objetivos que guían la toma de decisiones. Se presenta los principales aspectos relacionados a las preferencias de las alternativas en la toma de decisiones, criterios y modos de elección; asimismo, se presenta las herramientas de evaluación de riesgo.

Profesor Hossein Arsham   

---

   MENU

1. Introducción y resumen
2. Modelos Probabilísticos: De los Datos a un Conocimiento Decisivo
3. Análisis de Decisión: Tomando Decisiones Justificables y Defendibles
4. Elementos de los Modelos de Análisis de Decisión
5. Toma de Decisiones bajo Incertidumbre Pura: Los materiales se encuentran presentados en el contexto de selección de portafolios financieros.
6. Limitaciones de la Toma de Decisiones bajo Incertidumbre Pura
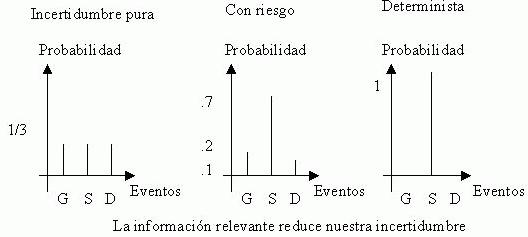
7. Manejar la Incertidumbre
8. Toma de Decisiones bajo Riesgo: Presentaciones en el contexto de selección de portafolios financieros
9. Tomando una Mejor Decisión mediante la Obtención de Información Confiable. Las aplicaciones estan dibujadas del mercadeo de un Nuevo Producto.
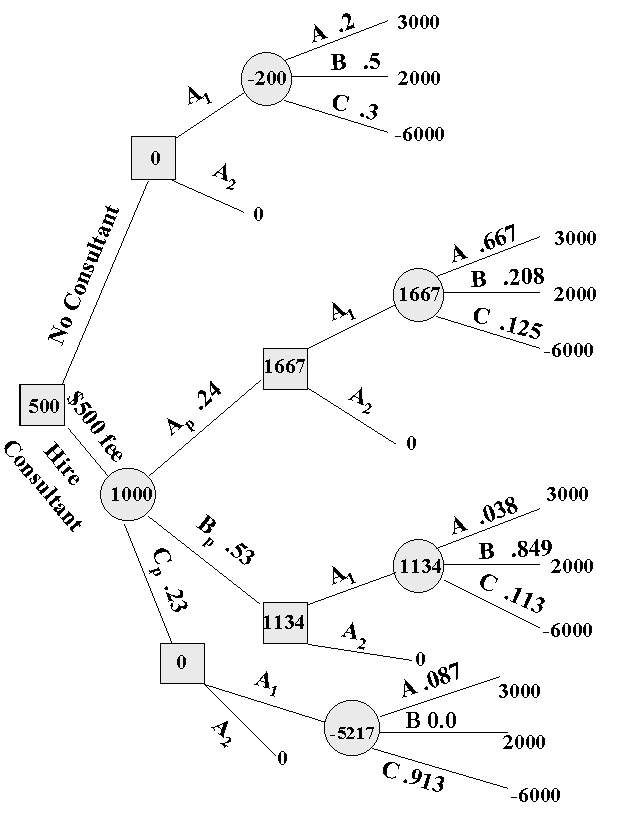
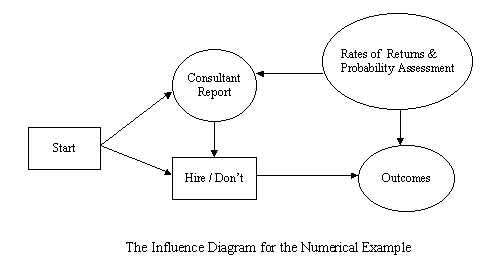
10. Arbol de Decisión y Diagrama de Influencia
11. Porque Gerentes Buscan los Consejos de las Firmas Consultoras
12. Revisar sus Expectativas y su Riesgo Asociado
13. Determinación de la Utilidad de los Tomadores de Decisión
14. Representación y Aplicaciones de la Función de Utilidad
15. Una Clasificación A de Actitudes Relativas de los Tomadores de Decisiones con Respecto al Riesgo y su Impacto
16. El Descubrimiento y la Gerencia de las Pérdidas
17. Riesgo: La Palabra de las Cinco Letras
18. Prioridad de los Factores de Decisión y Análisis de Estabilidad
19. JavaScript y Objetos de Aprendizaje E-labs
    

        Sitios Adjuntos:

20. Ciencia de la Administración Aplicada para Gerentes y Lideres Gerenciales,
    Sitio Espejo para España,  Sitio Espejo para América Latina.
21. Razonamiento Estadístico para la Toma de Decisiones Gerenciales,  
    Sitio Espejo para España,  Sitio Espejo para América Latina.
22. Modelos Deterministas: Optimización lineal,
    Sitio Espejo para España,  Sitio Espejo para América Latina.
23. Optimización de Enteros y Modelos de Redes,
    Sitio Espejo para España,  Sitio Espejo para América Latina.
24. Introducción a la Teoría de Juegos,  
    Sitio Espejo para España,  Sitio Espejo para América Latina.
25. Razonamiento Estadístico para la Toma de Decisiones Gerenciales,  
    Sitio Espejo para España,  Sitio Espejo para América Latina.
26. Construcción de Regiones de Sensibilidad General de Programación Lineal,
    Sitio Espejo para España,  Sitio Espejo para América Latina.
27. Toma de Decisiones con Periodos de Tiempo Crítico en Economía y Finanzas,  
    Sitio Espejo para España,  Sitio Espejo para América Latina.
28. Una Clasificación de JavaScript Estadíticos,  
    Sitio Espejo para España,  Sitio Espejo para América Latina.

Para buscar el sitio, pruebe en Edición | Encontrar en la página [Ctrl + f]. Escribir una palabra o frase en el espacio del diálogo. Por ejemplo "riesgo" o "utilidad" Si el primer resultado de la palabra o la frase no es el que vos buscaba, intenta con Encuentra Próximo.

---

Introducción y resumen

El análisis de decisión proporciona un soporte cuantitativo a los tomadores de decisiones en todas las áreas tales como ingenieros, analistas en las oficinas de planificación, agencias publicas, consultores en proyectos de gerencia, planificadores de procesos de producción, analistas financieros y de economía, expertos en diagnósticos de soportes medico y tecnológicos e infinidad de otras áreas.

Aproximación Progresiva al Modelado: El modelado para la toma de decisiones envuelve a dos partes diferentes, una es el tomador de decisiones y la otra es el constructor del modelo, conocido como el analista.El analista debe asistir al tomador de decisiones en el proceso de decidir. Por lo tanto, el analista debe estar equipado con mas que un conjunto de métodos analíticos.

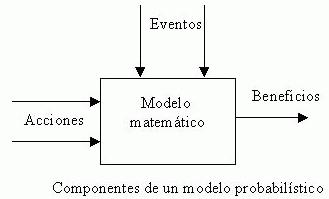
Los especialistas en la construcción de modelos se encuentran normalmente tentados a estudiar el problema, y luego aislarse a desarrollar un modelo matemático para ser utilizado por el gerente (es decir, el tomador de decisiones.) Desgraciadamente el gerente podría no entender el modelo, por lo tanto podría usarlo ciegamente o simplemente rechazarlo. El especialista podría sentir que el gerente es exageradamente ignorante y poco sofisticado para valorar el modelo, mientras que el gerente podría pensar que el analista vive en un mudo de fantasía de supuestos irreales y de lenguaje matemático irrelevante.

Dichos problemas de mal interpretación y de incomunicación pueden ser evitados si el gerente trabaja en conjunto con el especialista en el desarrollo de; primero un modelo simple que proporcione un análisis crudo pero entendible. Luego que el gerente le ha ganado confianza al modelo, detalles adicionales y una mayor sofisticación pueden ser agregados, quizás de una forma lenta y progresiva. Este proceso requiere la inversión de tiempo por parte del gerente e interés sincero por parte del analista para solucionar los problemas reales del gerente, en vez de tratar de crear y explicar modelos extremadamente sofisticados. Esta construcción progresiva de modelos es comúnmente referida como la aproximación de bootstrapping y es el factor más importante en la determinación de un modelo de decisión de implementación exitosa. Adicionalmente, el acercamiento de bootstrapping simplifica las dificultades del proceso de validación y verificación del modelo.

¿Que es un Sistema?: Los sistemas están formados por partes que son puestas en funcionamiento juntas de una forma particular para obtener un objetivo. La relación entre las partes determina lo que el sistema hace y como funciona en general. Por lo tanto, las relaciones en el sistema son normalmente mas importantes que cada parte individualmente. En general, los sistemas que son construidos como bloques de otros sistemas se llaman subsistemas.

La Dinámica de un Sistema: Un sistema que no cambia es un sistema estático (es decir, determinístico.) Muchos de los sistemas a los cuales pertenecemos son sistemas dinámicos, los cuales cambian a través del tiempo. Cuando nos referimos a que cambian a través del tiempo es de acuerdo al comportamiento del sistema. Cuando el desarrollo del sistema sigue un patrón típico decimos que el mismo tiene un patrón de comportamiento. El sistema será estático o dinámico dependiendo del horizonte temporal que se escoja y de las variables en las cuales se está concentrado. El horizonte temporal es el periodo de tiempo dentro del cual se estudia el sistema. Las variables son valores cambiables dentro del sistema.

En los modelos determinísticos, una buena decisión es juzgada de acuerdo a los resultados. Sin embargo, en los modelos probabilísticos, el gerente no esta preocupado solamente por los resultados, sino que también con la cantidad de riesgo que cada decisión acarrea.

Como un ejemplo de la diferencia entre los modelos probabilísticos versus determinísticos, considere el pasado y el futuro: Nada que hagamos ahora puede cambiar el pasado, pero cualquier cosa que hacemos influencia y cambia el futuro, a pesar de que el futuro tiene un elemento de incertidumbre. Los gerentes se encuentran mucho mas cautivados por darle forma al futuro que por la historia pasada.

El concepto de probabilidad ocupa un lugar importante en el proceso de toma de decisiones, ya sea que el problema es enfrentado en una compañía, en el gobierno, en las ciencias sociales, o simplemente en nuestra vida diaria. En muy pocas situaciones de toma de decisiones existe información perfectamente disponible – todos los hechos necesarios.- La mayoría de las decisiones son hechas de cara a la incertidumbre. La probabilidad entra en el proceso representando el; rol de sustituto de la certeza – un sustituto para el conocimiento completo.

Los modelos probabilísticos están ampliamente basados en aplicaciones estadísticas para la evaluación de eventos incontrolables (o factores), así como también la evaluación del riesgo de sus decisiones. La idea original de la estadística fue la recolección de información sobre y para el Estado. La palabra estadística no se deriva de ninguna raíz griega o latina, sino de la palabra italiana state. La probabilidad tiene una historia mucho mas larga. LaProbabilidad se deriva del verbo probar lo que significa "averiguar" lo que no es tan fácil de obtener o entender. La palabra "prueba" tiene el mismo origen el cual proporciona los detalles necesarios para entender lo que se requiere que sea cierto.

Los modelos probabilísticos son vistos de manera similar que a un juego; las acciones están basadas en los resultados esperados. El centro de interés se mueve desde un modelo determinístico a uno probabilístico usando técnicas estadísticas subjetivas para estimación, prueba y predicción. En los modelos probabilísticos, el riesgo significa incertidumbre para la cual la distribución de probabilidad es conocida. Por lo tanto, la evaluación de riesgo significa un estudio para determinar los resultados de las decisiones junto a sus probabilidades.

Los tomadores de decisiones generalmente se enfrentan a severa escasez de información. La evaluación de riesgo cuantifica la brecha de información entre lo que es conocido y lo que necesita saber para tomar una decisión óptima. Los modelos probabilístico son utilizados para protegerse de la incertidumbre adversa, y de la explotación de la propia incertidumbre.

La Dificultad en la Evaluación de la Probabilidad se obtiene de la información, la cual es escasa, vaga, inconsistente, o incompleta. Una afirmación tal y como que "la probabilidad de una baja de electricidad se encuentra entre 0,3 y 0,4" es mas natural y realista que su contraparte “exacta” de que "la probabilidad de una baja de electricidad es 0,36342."

Es una tarea desafiante comparar varios cursos de acción y finalmente seleccionar la acción que se va a realizar. En determinados casos, esta tarea puede resultar excesivamente desafiante. Las dificultades de la toma de decisiones están representadas por la complejidad de las alternativas de decisión. La capacidad que tiene un decisor de procesar información limitada es un factor de exigencia ya cuando se consideran las implicancias de un solo curso de acción, pero en muchas decisiones se deben visualizar y comparar las implicancias de varios cursos de acción. Además, hay factores desconocidos que se inmiscuyen en la situación problemática; rara vez se conoce con certeza el resultado. La mayoría de las veces, el resultado depende de las reacciones de otras personas que quizás ni siquiera saben qué van a hacer. No es de sorprender entonces que a veces los decidores pospongan la elección lo más posible y que luego decidan sin intentar considerar todas las implicancias de su decisión.

La toma de una decisión, fundamentalmente, tiene que ver con combinar información sobre probabilidades con información sobre deseos e intereses. ¿Cuántas ganas tienes de conocer a esa mujer? ¿Cuán importante es la salida? ¿Cuánto vale ese premio?

Abordar las decisiones como si fueran apuestas es la base de la teoría de la decisión. Significa que tenemos que compensar el valor de un cierto resultado contra su probabilidad.

Para operar según los cánones de la teoría de la decisión debemos hacer cálculos del valor de un cierto resultado y sus probabilidades, y a partir de allí de las consecuencias de nuestras elecciones.

El origen de la teoría de la decisión para la toma de decisiones se deriva de la economía, en el área de la función de la utilidad del pago. Propone que las decisiones deben tomarse calculando la utilidad y la probabilidad de rangos de opciones, y establece estrategias para una buena toma de decisiones:

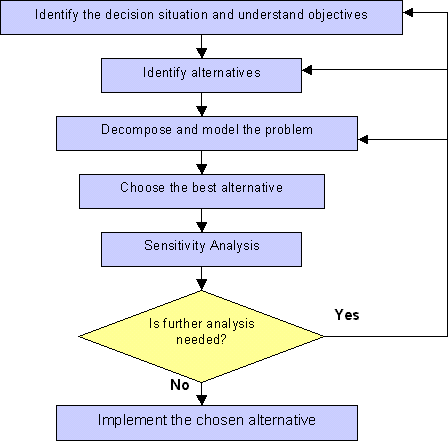
Este sitio web muestra el proceso de análisis de alternativas para la toma de decisiones publicas y privadas, usando diferentes criterios de decisión, diferentes tipos de información e información de calidad variable. Describe los elementos usados en el análisis de las alternativas de decisión y elección, así como también las metas y objetivos que guían la toma de decisiones. Se presenta los principales aspectos relacionados a las preferencias de las alternativas en la toma de decisiones, criterios y modos de elección; asimismo, se presenta las herramientas de evaluación de riesgo. En la sección siguiente examinaremos aspectos claves relacionados con las preferencias que puede tener un decisor en relación con las alternativas, los criterios de elección y las modalidades de elección.

Los objetivos son importantes, tanto para identificar los problemas como para evaluar las soluciones alternativas. En la evaluación de alternativas, los objetivos del decisor deben expresarse como criterios que reflejen los atributos de las alternativas relevantes para la elección.

El estudio sistemático de la toma de decisiones proporciona el marco para escoger cursos de acción en situaciones complejas, inciertas o dominadas por conflictos. La elección entre acciones posibles y la predicción de resultados esperados resultan del análisis lógico que se haga de la situación de decisión.

Un Inconveniente Posible en la Aproximación del Análisis de Decisión: Usted ya podría haber notado que el criterio anterior siempre resulta en la selección de un solo curso de acción. Sin embargo, en muchos problemas de decisión, el tomador de decisiones desearía la combinación de algunas acciones. Por ejemplo, en un problema de inversión, el inversionista desearía distribuir los activos entre una mezcla de opciones de forma tal de optimizar los retornos de portafolio. Visite la pagina web de Teoría de Juegos con Aplicaciones el cual está diseñado para una estrategia óptima mixta.

---

Modelos Probabilísticos: De los Datos a un Conocimiento Decisivo

El conocimiento es lo que sabemos. La información es la comunicación de conocimientos. En cada intercambio de conocimientos, hay un remitente y un receptor. El remitente hace común lo que es privado, hace la información, la comunicación. La información se puede clasificar como formas explícitas y tácitas. La información explícita se puede explicar de forma estructurada, mientras que la información tácita es inconsistente e imprecisa de explicar.

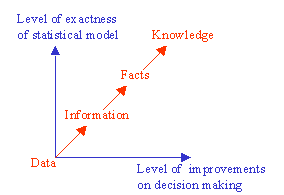
Los datos son conocidos como información cruda y no como conocimientos en sí. La secuencia que va desde los datos hasta el conocimiento es (observe el siguiente cuadro): de los Datos (Data) a la Información (Information), de la Información (Information) a los Hechos (Facts), y finalmente, de los Hechos (Facts) al Conocimiento (Knowledge) . Los datos se convierten en información, cuando se hacen relevantes para la toma de decisión a un problema. La información se convierte en hecho, cuando es respaldada por los datos. Los hechos son lo que los datos revelan. Sin embargo el conocimiento instrumental es expresado junto con un cierto grado estadístico de confianza (gl).

Los hechos se convierten en conocimiento, cuando son utilizados en la complementación exitosa de un proceso de decisión. Una vez que se tenga una cantidad masiva de hechos integrados como conocimiento, entonces su mente será sobrehumana en el mismo sentido en que, con la escritura, la humanidad es sobrehumana comparada a la humanidad antes de escribir. La figura siguiente ilustra el proceso de razonamiento estadístico basado en datos para construir los modelos estadísticos para la toma de decisión bajo incertidumbre.

de donde:

Level of Exactness of Statistical Model = Nivel de Exactitud del Modelo Estadístico.

Level of improvements on decisión making = Nivel de Mejoramiento en la Toma de Decisiones

La figura anterior representa el hecho que a medida que la exactitud de un modelo estadístico aumenta, el nivel de mejoramiento en la toma de decisión aumenta. Esta es la razón del porqué necesitamos la estadística de negocio. La estadística se creo por la necesidad de poner conocimiento en una base sistemática de la evidencia. Esto requirió un estudio de las leyes de la probabilidad, del desarrollo de las propiedades de medición, relación de datos.

La inferencia estadística intenta determinar si alguna significancia estadística puede ser adjunta luego que se permita una variación aleatoria como fuente de error. Una inteligente y crítica inferencia no puede ser hecha por aquellos que no entiendan el propósito, las condiciones, y la aplicabilidad de las de diversas técnicas para juzgar el significado.

Considerando el ambiente de la incertidumbre, la posibilidad de que “las buenas decisiones” sean tomadas incrementa con la disponibilidad “de la buena información”. El chance de la disponibilidad de “la buena información” incrementa con el nivel de estructuración del proceso de Dirección de Conocimiento. La figura anterior también ilustra el hecho que mientras la exactitud de un modelo estadístico aumenta, el nivel de mejora en la toma de decisiones aumenta.

El conocimiento es mas que simplemente saber algo técnico. El conocimiento necesita la sabiduría. La sabiduría es el poder de poner nuestro tiempo y nuestro conocimiento en el uso apropiado. La sabiduría viene con edad y experiencia. La sabiduría es la aplicación exacta del conocimiento exacto. La sabiduría es sobre saber como algo técnico puede ser mejor utilizado para cubrir las necesidades de los encargados de tomar decisiones. La sabiduría, por ejemplo, crea el software estadístico que es útil, más bien que técnicamente brillante. Por ejemplo, desde que la Web entró en el conocimiento popular, los observadores han notado que esto pone la información en nuestras manos, pero guardar la sabiduría fuera de nuestro alcance. HR>

Proceso de Toma de Decisiones Estadísticas

A diferencia de los procesos de toma de decisiones determinísticas tal como, optimización lineal resuelto mediante sistema de ecuaciones, sistemas paramétricos de ecuaciones y en la toma de decisión bajo pura incertidumbre, las variables son normalmente más numerosas y por lo tanto más difíciles de medir y controlar. Sin embargo, los pasos para resolverlos son los mismos. Estos son:

1. Simplificar
2. Construir un modelo de decisión
3. Probar el modelo
4. Usando el modelo para encontrar soluciones:
   • El modelo es una representación simplificada de la situación real
   • No necesita estar completo o exacto en todas las relaciones
   • Se concentra en las relaciones fundamentales e ignora las irrelevantes.
   • Este es entendido con mayor facilidad que un suceso empírico (observado), por lo tanto permite que el problema sea resuelto con mayor facilidad y con un mínimo de esfuerzo y pérdida de tiempo.
5. El modelo puede ser usado repetidas veces para problemas similares, y además puede ser ajustado y modificado.

Afortunadamente, los métodos probabilísticos y estadísticos para el análisis de toma de decisiones bajo incertidumbre son más numerosos y mucho más poderosos que nunca. Las computadoras hacen disponible muchos usos prácticos. Algunos de los ejemplos de aplicaciones para negocios son los siguientes:

• Un auditor puede utilizar técnicas de muestreo aleatorio para auditar las cuentas por cobrar de un cliente.
• Un gerente de planta puede utilizar técnicas estadísticas de control de calidad para asegurar la calidad de los productos con mínima inspección y menor número de pruebas.
• Un analista financiero podría usar métodos de regresión y correlación para entender mejor la analogía entre los indicadores financieros y un conjunto de otras variables de negocio.
• Un analista de mercadeo podría usar pruebas de significancia para aceptar o rechazar una hipótesis sobre un grupo de posibles compradores a los cuales la compañía esta interesada en vender sus productos.
• Un gerente de ventas podría usar técnicas estadísticas para predecir las ventas de los próximos periodos.

---

Análisis de Decisiones: Tomando Decisiones Justificables y Defendibles

El análisis de decisiones es la disciplina que consiste en evaluar alternativas complejas en términos de valores (habitualmente en $ porque es lo que a los gerentes les importa) y de incertidumbre (lo que no conocemos). El análisis de decisiones brinda información sobre las diferencias entre las alternativas definidas, y genera sugerencias de nuevas y mejores alternativas. Usamos números para cuantificar valores e incertidumbres subjetivas, lo cual nos permite comprender la situación de decisión. Los resultados numéricos deben reconvertirse para generar información cualitativa.

Los seres humanos pueden comprender, comparar y manipular números. Por lo tanto, para crear un modelo de análisis de decisiones es necesario crear la estructura del modelo y asignar las probabilidades y los valores para poblar el modelo de computación. Aquí se incluyen los valores para las probabilidades, las funciones de valor para evaluar alternativas, las ponderaciones de valor para medir la concesión que se debe hacer entre los objetivos, y la preferencia de riesgo.

Una vez definida la estructura y los números, el análisis puede comenzar. El Análisis de Decisiones implica mucho más que calcular la utilidad esperada y ponderada de cada alternativa. Si nos detuviéramos aquí, los decisores no tendrían demasiada información. Tenemos que examinar la sensibilidad de la utilidad esperada y ponderada para las probabilidades clave, y los parámetros de ponderación y preferencia de riesgo. Como parte del análisis de sensibilidad podemos calcular el valor de la información perfecta para incertidumbres que han sido modelizadas explícitamente.

Entre las comparaciones cuantitativas adicionales se incluye la comparación directa de la utilidad ponderada para dos alternativas en todos los objetivos y la comparación de todas las alternativas en dos objetivos seleccionados, demostrando la optimalidad de Pareto para estos dos objetivos.

La complejidad del mundo moderno, junto con la cantidad de Información, la Incertidumbre y el Riesgo, requieren un marco racional para la toma de decisiones. Las metas del análisis de decisiones son las siguientes: incorporar orientación, información, discernimiento y estructura al proceso de toma de decisión, para que ésta pueda ser mejor y más "racional".

Toda decisión necesita un decisor responsable. El decisor tiene varias alternativas, y debe elegir una. El objetivo del decisor es elegir la mejor alternativa. Después de que se ha tomado la decisión, pueden producirse eventos sobre los que el decisor no tiene control. Cada combinación de alternativas elegida, seguida por un evento, conduce a un resultado con algún valor mensurable. Los gerentes toman decisiones en situaciones complejas. Las matrices de árbol de decisiones y pago describen estas situaciones y añaden estructura a los problemas.

---

Elementos de los Modelos de Análisis de Decisión

Las teorías y las técnicas matemáticas que se toman en consideración en el análisis de decisiones se ocupan de las teorías de elección prescriptivas (acción). Es decir, la cuestión aquí es ver exactamente de qué modo se comporta un decisor cuando se enfrenta a una elección entre cursos de acción, cuyos resultados están regidos por el azar o las acciones de los competidores.

El análisis de decisiones es un proceso que le permite al decisor seleccionar una decisión (sólo una) entre un conjunto de alternativas posibles de decisión, cuando existe incertidumbre con respecto al futuro, con el objetivo de optimizar el pago (retorno) resultante, en términos de algún tipo de criterio de decisión numérico. Los elementos de los problemas de análisis de decisiones son los siguientes:

1. Hay un decisor responsable individual. Por ejemplo, el CEO de una compañía que quizás deba rendir cuentas ante los accionistas.
   
2. Un número finito de eventos (futuros) posibles, llamados Estados de la Naturaleza, es decir, un conjunto de escenarios posibles. Las circunstancias en las cuales se toma una decisión se llaman estados de la naturaleza. Los estados de la naturaleza se identifican y agrupan en el conjunto S; los miembros se denotan como s. El conjunto S es un grupo de conjuntos mutuamente excluyentes. Es decir, sólo puede ocurrir un estado de la naturaleza. ¿Qué puede hacer la naturaleza?
3. 3. Un número finito de alternativas posibles de decisión. Hay una acción a, miembro del conjunto A, que puede ser adoptada por el decisor. Sólo puede adoptar una. ¿Qué puedo hacer? Una buena decisión requiere buscar un conjunto más rico de alternativas que las que se presentaron inicialmente o que las aceptadas tradicionalmente.
   Sea breve en la parte de la lógica y la razón de su decisión. Es probable que existan mil cosas en un automóvil, pero usted no las necesita todas para tomar la decisión. Con media docena es suficiente.
4. La manera más sencilla de formular el problema de decisión es usando una matriz de beneficios (tabla). Hay una matriz de beneficios X bien definida, monetaria (y luego de utilidad) sobre dos conjuntos de dominio dimensionales A y S. Las filas y las columnas se asignan a las alternativas de decisión posibles y a los estados posibles de la naturaleza, respectivamente.
   Normalmente no es tarea sencilla construir esta matriz; por lo tanto, puede requerir algo de práctica.

Fuente de Errores en la Toma de Decisiones: La fuente principal de errores en los problemas de toma de decisiones arriesgadas son las presunciones falsas, no tener una estimación exacta de las probabilidades, depender de la expectativa, dificultades en medir la función de utilidad, y los errores de pronóstico.

Componentes de un Modelo Probabilístico

Considere el siguiente Problema de Decisión de Inversión:

Ejemplo de decisión de inversión:

		Estados de la Naturaleza
		Crecimiento	Crecimiento medio	Sin cambio	Bajo
		C	CM	SC	B
	Bonos	12%	8	6	3
Cursos de Acción	Acciones	15	7	3	-2
	Depósito	7	7	7	7

Los estados de la naturaleza son los estados de la economía durante un año. El problema es decidir que acciones tomar entre los tres cursos posibles, con las tasas de retorno dadas tal y como son mostradas en la tabla.

---

Hacer Frente a la Incertidumbre

Continuidad de Incertidumbre Pura y de Certidumbre: El dominio de los modelos de análisis de decisiones está entre los siguientes dos casos extremos, dependiendo del grado de conocimiento que tenemos sobre el resultado de nuestras acciones, como se muestra a continuación:

Uno de los "polos" de esta escala es determinista, como en el problema del carpintero. El "polo" opuesto es la incertidumbre pura. Entre estos dos hay problemas con riesgo. La idea principal, aquí, es que para un problema dado, el grado de certidumbre varía según el gerente, dependiendo de la cantidad de conocimiento que cada gerente tenga sobre el mismo problema y refleja la solución diferente que cada persona recomienda.

La probabilidad es un instrumento para medir los chances de que un evento ocurra. Cuando se usa probabilidad se expresa la incertidumbre, el lado determinista tiene una probabilidad de 1 (o cero), mientras que el otro extremo tiene una probabilidad plana (todas igualmente probables). Por ejemplo, si usted tiene certidumbre de la ocurrencia (o no ocurrencia) de un evento, usa una probabilidad de uno (o cero). Si usted tiene incertidumbre, entonces usa la expresión "En realidad no sé", por lo tanto, puede o no ocurrir con una probabilidad del 50%. Esta es la noción de Bayes de que la evaluación de la probabilidad siempre es subjetiva. Es decir, la probabilidad siempre depende de cuánto conoce el decisor. Si sabe todo lo que puede saber, la probabilidad pasará a ser 1 o 0.

Las situaciones de decisión con incertidumbre plana presentan el riesgo más grande. Para fines de simplicidad, considere el caso en que hay sólo dos resultados con una probabilidad de p. Así, la variación en los estados de la naturaleza es p(1-p). Esta variación es la mayor si definimos p = 50%. Es decir, igual chance para cada resultado. En tal caso, la calidad de la información está en su nivel más bajo. Recuerden de Estadística que la calidad de la información y la variación están inversamente relacionadas. Una variación mayor de los datos implica una disminución en la calidad de los datos (es decir, de la información).

La información relevante para resolver un problema de decisión achica nuestra probabilidad plana. La información de utilidad desplaza la ubicación de un problema desde el "polo" de la pura incertidumbre hacia el "polo" determinista. La información relevante y útil achica la incertidumbre. .

La evaluación de la probabilidad no es más que la cuantificación de la incertidumbre. En otras palabras, la cuantificación de la incertidumbre permite comunicar la incertidumbre entre las personas, como la incertidumbre entre eventos, estados del mundo, creencias, etc. La probabilidad es la herramienta para comunicar la incertidumbre y para manejar la incertidumbre (domar el cambio).

Existen tipos diferentes de modelos de decisión que ayudan a analizar distintos escenarios, dependiendo de la cantidad y el grado de conocimiento que tengamos. Los tres tipos más ampliamente utilizados son:

• Decisión tomada con pura incertidumbre,
• Decisión tomada con riesgo,
• Decisión tomada comprando información (empujando el problema hacia el "polo" determinista)

En las decisiones tomadas con pura incertidumbre, el decisor no tiene ningún conocimiento, ni siquiera de la probabilidad de ocurrencia de cualquier estado de la naturaleza. En estas situaciones, el comportamiento del decisor se basa puramente en su su actitud hacia la incógnita. Algunos de estos comportamientos son los optimistas, los pesimistas y los de arrepentimiento, entre otros. La persona más optimista que conocí fue sin duda un joven artista en París quien, sin un franco en el bolsillo, fue a un restaurante elegante y ordenó docenas de ostras, con la esperanza de encontrar la perla que pagara la cuenta.

Optimista: El vaso está medio lleno.
Pesimista: El vaso está medio vacío.
Gerente: El vaso es el doble de grande de lo necesario.

Observe que esta categoría de problemas (es decir, los problemas con pura incertidumbre) resultan apropiados sólo para la toma de decisiones en la vida privada. No obstante, la persona pública (es decir, el gerente) tiene que tener cierto conocimiento de los estados de la naturaleza, para poder predecir las probabilidades de cada estado. De lo contrario no podrá tomar una buena decisión que sea razonable y defendible.

Siempre que un decisor tiene cierto conocimiento sobre los estados de la naturaleza puede asignar una probabilidad subjetiva a la ocurrencia de cada estado. Y cuando lo hace, el problema se clasifica como toma de decisiones bajo riesgo.

En muchos casos, el decisor puede necesitar la opinión de un especialista para limitar sus incertidumbres con respecto a la probabilidad de cada estado de la naturaleza. En tal caso, el decisor puede comprar información relevante a especialistas, para poder tomar una mejor decisión. El procedimiento para incorporar el asesoramiento de un experto en las incertidumbres del decisor se conoce como el abordaje de Bayes.

Por ejemplo, en una situación donde se debe tomar una decisión de inversión, se debe responder la siguiente pregunta: ¿En qué estado estará la economía el año próximo? Supongamos que limitamos las posibilidades a: Crecimiento (G), Igualdad (S), o Declinación (D); entonces, una representación típica de nuestra incertidumbre podría ilustrarse de la siguiente manera:

---

Toma de decisiones con pura incertidumbre

Cuando las decisiones se toman con pura incertidumbre, el decisor no tiene conocimiento de los resultados de ninguno de los estados de la naturaleza y/o es costoso obtener la información necesaria. En tal caso, la decisión depende meramente del tipo de personalidad que tenga el decisor.

Comportamiento según los tipos de personalidad y la toma de decisiones con pura incertidumbre:

Pesimismo, o Conservador (Maximin). Hipótesis de mínima. Las cosas malas siempre me suceden a mí.

	B	3
a) Escriba el número mínimo en cada fila de acción.	S	-2
b) Elija el número máximo y realice esa acción.	D	7	*

Optimismo, Agresivo (Maximax). Las cosas buenas siempre me suceden a mí.

	B	12
a) Escriba el número máximo en cada fila de acción.	S	15	*
b) Elija el número máximo y realice esa acción.	D	7

Coeficiente de Optimismo (Indice de Hurwicz), ). A mitad de camino: Ni demasiado optimista ni demasiado pesimista:

a) Elija a entre 0 y 1, 1 significa optimista y 0 significa pesimista,

b) Elija los números más alto y más bajo para cada acción,

c) Multiplique el beneficio más alto (en el sentido de las filas) por a y el más bajo por (1- a ),

d) Opte por el curso de acción que da la suma más alta.

Por ejemplo, para a = 0,7, tenemos:

B		(0,7*12)	+		(0,3*3)	=	9,3
S		(0,7*15)	+		(0,3*-2)	=	9,9 *
D		(0,7*7)	+		(0,3*7)	=	7

Mínimo arrepentimiento: (Pérdida de Oportunidad de Savag). Odio las lamentaciones. Debo minimizar las situaciones deplorables. Mi decisión debe ser tal que valga la pena repetirla. Sólo debería hacer las cosas que siento que podría repetir con placer.

El arrepentimiento es el beneficio o rédito de la que hubiera sido la mejor decisión, dadas las circunstancias, menos el beneficio de la decisión tomada concretamente, dadas las circunstancias.

a) Configure una tabla de arrepentimiento: Tome el número más alto de cada una de las columnas correspondientes a los estados de la naturaleza (por ejemplo, L) y réstele todos los números de dicha columna, es decir, L - Xi,j.

La Matriz de Arrepentimiento
	C	CM	SC	B	Paso b
Bonos	(15-12)	(8-8)	(7-6)	(7-3)	4 *
Acciones	(15-15)	(8-7)	(7-3)	(7+2)	9
Depósito	(15-7)	(8-7)	(7-7)	(7-7)	8

b) Elija el número máximo de cada acción,
c) Elija el número mínimo en Paso b, y adopte esa acción.

Toma de decisiones con pura incertidumbre JavaScript E-labs.

Limitaciones de la Toma de Decisiones bajo Pura Incertidumbre

1. En general el análisis de decisión se asume que el tomador de decisiones se enfrenta un problema donde el o ella debe escoger por lo menos y como máximo una opción del grupo de opciones. En algunos casos estas limitaciones pueden ser superados mediante la formulación de una toma de decisión bajo incertidumbre como un juego suma cero de dos personas.

2. En la toma de decisiones bajo incertidumbre pura, el tomador de decisiones no tiene conocimientos sobre cual estado de la naturaleza es más “probable” que ocurra. El o ella probablemente ignora los estados de la naturaleza por lo tanto no podría estar pesimista u optimista. En tal caso, el tomador de decisiones emboca las condiciones de seguridad.

3. Note que cualquier técnica utilizada en la toma de decisiones bajo incertidumbre pura, es solo apropiada para las decisiones de la vida privada. Adicionalmente, una persona pública (por ejemplo, se gerente) debe tener algunos conocimientos sobre el estado de la naturaleza tal que prediga las probabilidades de varios estados de la naturaleza. De lo contrario, el tomador de decisiones no es capaz de proporcionar una decisión razonable y defendible.

A usted podría gustarle utilizar el JavaScript E-lab de Toma de Decisiones Bajo Pura Incertidumbre para comprobar sus cálculos y realizar experimentaciones numéricas para una comprensión mas profunda y un análisis de estabilidad mas de sus decisiones mediante la alteración de los parámetros del problema.

---

Toma de Decisiones Bajo Riesgo

El riesgo implica cierto grado de incertidumbre y la habilidad para controlar plenamente los resultados o consecuencias de dichas acciones. El riesgo o la eliminación del mismo es un esfuerzo que los gerentes deben realizar. Sin embrago, en algunos casos la eliminación de cierto riesgo podría incrementar riesgos de otra índole. El manejo efectivo del riesgo requiere la evaluación y el análisis del impacto subsiguiente del proceso de decisión. Este proceso permite al tomador de decisiones evaluar las estrategias alternativas antes de tomar cualquier decisión. El proceso de decisión se describe a continuación:

1. El problema esta definido y todas las alternativas confiables han sido consideradas. Los resultados posibles para cada alternativa son evaluados.
2. Los resultados son discutidos de acuerdo a su reembolso monetario o de acuerdo a la ganancia neta en activos o con respecto al tiempo.
3. Varios valores inciertos son cuantificados en términos de probabilidad.
4. La calidad de la estrategia óptima depende de la calidad con que se juzgue. El tomador de decisiones deberá examinar e identificar la sensitividad de la estrategia optima con respecto a los factores cruciales.

   Cuando el decisor posee algún conocimiento sobre los estados de la naturaleza puede asignarle a la ocurrencia de cada estado alguna estimación subjetiva de probabilidad. En estos casos, el problema se clasifica como de toma de decisiones con riesgo. El decisor puede asignar probabilidades a la ocurrencia de los estados de la naturaleza. El proceso de toma de decisión con riesgo es el siguiente:

   a) Use la información que tenga para asignar su parecer personal (llamado probabilidades subjetivas) sobre el estado de la naturaleza, p(s);

   b) Cada curso de acción tiene asociado un determinado beneficio con cada uno de los estados de la naturaleza, X(a,s);

   c) Calculamos el beneficio esperado, también llamado riesgo o R, correspondiente a cada curso de acción como R(a) = Sumas de [X(a,s) p(s)];

   d) Aceptamos el principio que dice que deberíamos actuar para minimizar (o maximizar) el beneficio esperado;

   e) Ejecute la acción que minimice R(a).

   
   

   Beneficio esperado: El resultado real no será igual al valor esperado. Lo que se obtiene no es lo que se espera, es decir, las "Grandes Expectativas".

   a) Con cada acción, multiplique la probabilidad y el beneficio y luego sume: Elija el número más grande y adopte esa acción. b) Agregue el resultado por fila, c) Seleccione el número más grande y tome esa acción.

   	C (0,4)		CM (0,2)		SC (0,3)		B (0,1)		Valor esperado
   Bonos	0,4(12)	+	0,2(8)	+	03(6)	+	0,1(3)	=	8,5*
   Acciones	0,4(15)	+	0,2(7)	+	0,3(3)	+	0,1(-2)	=	8,1
   Depósito	0,4(7)	+	0,2(7)	+	0,3(7)	+	0,1(7)	=	7

   Los estados más probables de la naturaleza: (apropiado para decisiones no repetitivas)

   a) Tome el estado de la naturaleza que tiene la probabilidad más alta (rompa los empates arbitrariamente),

   b) En esa columna, elija la acción que tiene el mayor beneficio,

   En nuestro ejemplo numérico, el Crecimiento tiene una chance del 40%, por eso debemos comprar Acciones.

   Pérdida de oportunidad esperada (POE):

   a) Configure una matriz de beneficios de la pérdida tomando el número más alto de las columnas correspondientes a los estados de la naturaleza (digamos, L) y réstele todos los números de esa columna, L - Xij.

   b) Para cada acción, multiplique la probabilidad y las pérdidas, luego agréguelas a cada acción,

   c) Seleccione la acción con el POE más pequeño

   
   

   Matriz de Beneficios de Pérdida
   	C (0,4)		CM (0,2)		SC(0,3)		B (0,1)	POE
   Bonos	0,4(15-12)	+	0,2(8-8)	+	0,3(7-6)	+	0,1(7-3)	1,9 *
   Acciones	0,4(15-15)	+	0,2(8-7)	+	0,3(7-3)	+	0,1(7+2)	2,3
   Depósito	0,4(15-7)	+	0,2(8-7)	+	0,3(7-7)	+	0,1(7-7)	3,4

   
   

   Cálculo del Valor Esperado de la Información Perfecta (VEIP)

   El VEIP nos ayuda a considerar el valor que tienen las personas informadas (por ejemplo, el demonio), que son las dueñas de la información perfecta. Recuerde que el VEIP = POE.

   a) Tome el beneficio máximo de cada estado de la naturaleza,

   b) Multiplique cada uno por la probabilidad de que ocurra ese estado de la naturaleza y luego súmelos,
   

   C	15(0,4)	=	6,0
   CM	8(0,2)	=	1,6
   SC	7(0,3)	=	2,1
   B	7(0,1)	=	0,7
   	+		----------
   			10,4

   
   

   VEIP = 10,4 - Beneficio Esperado = 10,4 – 8,5 = 1,9. Verifique si la PEO = VEIP

   Por lo tanto, si la información cuesta más del 1.9% de la inversión no la compre. Por ejemplo, si usted va a invertir $100.000, el máximo que deberá pagar por la información que compre será de [100.000 * (1,9%)] = $1.900.

   Yo no sé nada: Todos los estados de la naturaleza tienen igual probabilidad. Como yo no sé nada sobre la naturaleza, todo es igualmente probable (Laplace):

   a) Para cada estado de la naturaleza ponga una probabilidad igual (es decir, probabilidad plana),
   b) Multiplique cada número por la probabilidad,

   	C	CM	SC	B	Beneficio esperado
   Bonos	0,25(12)	0,25(8)	0,25(6)	0,25(3)	7,25 *
   Acciones	0,25(15)	0,25(7)	0,25(3)	0,25(-2)	5,75
   Depósito	0,25(7)	0,25(7)	0,25(7)	0,25(7)	7

   c) Añada filas de cursos de acción y complete la columna Beneficio Esperado,
   d) Elija el número máximo en Paso c, y adopte ese curso de acción.

   Una Discusión Acerca de la Posibilidad de Pérdida esperada (Arrepentimiento Esperado): Comparando el resultado de una decisión con respecto a sus alternativas aparenta ser un componente importante en el proceso de toma de decisiones. Un factor importante es el sentimiento de arrepentimiento. Este ocurre cuando los resultados de las decisiones son comparados a los resultados que se hubieran obtenidos si se hubiera tomado una decisión diferente. Esto significa un contrastante desacuerdo, el cual resulta de la comparación de resultados como consecuencia de la misma decisión.

   Los resultados de arrepentimiento es la comparación de lo que se ha obtenido de una decisión con respecto a lo que hubiese ocurrido. Por lo tanto, esto depende de la disponibilidad de respuestas que reciben los tomadores de decisiones con respecto al resultado de la opción alternativa hubiera generado. Alterando el potencial de arrepentimiento mediante la manipulación de la resolución de la incertidumbre revela que el comportamiento de la toma de decisión que aparenta aversión al riesgo puede de hecho ser atribuida a la aversión al arrepentimiento.

   No existe indicativo de que el arrepentimiento pueda estar relacionado a la distinción entre actos y omisión. Algunos estudios han encontrado que el arrepentimiento es más intenso siguiendo una acción, que a una omisión. Por ejemplo, en un estudio, los participantes concluyeron que un tomador de decisiones que intercambia acciones de una compañía a otra y pierde dinero, se sentirá mas arrepentido que otro que no intercambia acciones pero que igualmente pierde dinero. Las personas normalmente asignan un mayor valor a un resultado inferior proveniente de una acción mas que al de una omisión. Presumiblemente, esta una manera de contrarrestar el arrepentimiento que podría resultar de una acción.

   A usted podría gustarle utilizar el JavaScript E-lab de Tomando Decisiones Riesgosas para comprobar sus resultados, y realizar experimentaciones numérica para una comprensión mas profunda, y análisis de estabilidad de sus decisiones mediante la alteración de los parámetros del problema.

   ---

   Cómo tomar una mejor decisión comprando información confiable (Abordaje de Bayes)

   En muchos casos, el decisor puede necesitar la opinión de un especialista para reducir sus incertidumbres con respecto a la probabilidad de cada uno de los estados de la naturaleza. Por ejemplo, consideremos el siguiente problema de decisión concerniente a la producción de un nuevo producto:

   
   

   		Estados de la naturaleza
   		Mucha venta	Venta media	Poca venta
   		A(0,2)	B(0,5)	C(0,3)
   A1	(desarrollar)	3000	2000	-6000
   A2	(no desarrollar)	0	0	0

   
   

   Las probabilidades de los estados de la naturaleza representan los distintos grados que tiene el criterio del decisor (por ejemplo, un gerente) con respecto a la ocurrencia de cada estado. Nos referiremos a estas evaluaciones subjetivas de la probabilidad como probabilidades "a priori".

   El beneficio esperado de cada curso de acción es A1 = 0,2(3000) + 0,5(2000) + 0,3(-6000) = -$200 y A2 = 0; entonces elegimos A2, que significa que no desarrollamos.

   Sin embargo, el gerente se siente algo reacio a tomar esta decisión; por ello solicita la asistencia de una firma de investigación de mercado. Ahora nos enfrentamos a una nueva decisión. Es decir, con cuál firma de investigación de mercado debe consultar su problema de decisión. De esta manera es que el gerente debe tomar una decisión acerca de cuán "confiable" es la firma consultora. Mediante muestreo y luego analizando el desempeño previo de la consultora debemos desarrollar la siguiente matriz de confiabilidad:

   		Qué sucedió realmente en el pasado
   		A	B	C
   Lo que el consultor	Ap	0,8	0,1	0,1
   predijo	Bp	0,1	0,9	0,2
   	Cp	0,1	0,0	0,7

   Todas las Firmas de Investigación de Mercado llevan registros (es decir, conservan datos históricos) del desempeño alcanzado en relación con las predicciones anteriores que hubieren formulado. Estos registros los ponen a disposición de sus clientes sin cargo alguno. Para construir una matriz de confiabilidad debe tomar en consideración los "registros de desempeño" de la Firma de Investigación de Mercado correspondientes a los productos que tienen mucha venta, y luego hallar el porcentaje de los productos que la Firma predijo correctamente que tendrían mucha venta, venta media y poca o ninguna venta. Estos porcentajes se representan como P(A_p|A) = 0,8, P(B_p|A) = 0,1, P(C_p|A) = 0,1, en la primera columna de la tabla anterior, respectivamente. Se debe efectuar un análisis similar para construir las otras columnas de la matriz de confiabilidad.

   Observe que para fines de consistencia, las entradas de cada columna en la matriz de confiabilidad deberían sumar uno.

   a) Tome las probabilidades y multiplíquelas "hacia abajo" en la matriz, y luego súmelas:

   b) SUMA es el resultado de sumar en sentido horizontal.
   c) Es necesario normalizar los valores (es decir, que las probabilidades sumen 1) dividiendo el número de cada fila por la suma de la fila hallada en el paso b.

   0,2	0,5	0,3
   A	B	C	SUMA
   0,2(0,8) = 0,16	0,5(0,1) = 0,05	0,3(0,1) = 0,03	0,24
   0,2(0,1) = 0,02	0,5(0,9) = 0,45	0,3(0,2) = 0,06	0,53
   0,2(0,1) = 0,02	0,5(0) = 0	0,3(0,7) = 0,21	0,23

   A	B	C
   (0,16/0,24)=0,667	(0,05/0,24)=0,208	(0,03/0,24)=0,125
   (0,02/0,53)=0,038	(0,45/0,53)=0,849	(0,06/0,53)=0,113
   (0,02/0,23)=0,087	(0/0,23)=0	(0,21/0,23)=0,913

   A usted podría gustarle utilizar el JavaScript E-lab de Aspectos Computacionales de la Probabilidad de Revisada de Bayes para comprobar sus cálculos, realizar experimentaciones numéricas, y realizar análisis de estabilidad de sus decisiones mediante la alteración de los parámetros del problema.

   d) Dibuje el árbol de decisiones. Muchos ejemplos gerenciales, como el de este ejemplo, involucran una secuencia de decisiones. Cuando una situación de decisión requiere que se tome una serie de decisiones, el abordaje de la tabla de pago puede no dar cabida a las múltiples capas de decisiones. Para ello se aplica el árbol de decisiones.

   ---

   Arbol de Decisiones y Diagrama de Influencia

   Aproximación del Arbol de decisiones: El árbol de decisiones es una representación cronológica del proceso de decisión, mediante una red que utiliza dos tipos de nodos: los nodos de decisión, representados por medio de una forma cuadrada (el nodo de elección), y los nodos de estados de la naturaleza, representados por círculos (el nodo de probabilidad). Dibuje la lógica del problema construyendo un árbol de decisiones. Para los nodos de probabilidad asegúrese de que las probabilidades en todas las ramas salientes sumen uno. Calcule los beneficios esperados retrocediendo en el árbol, comenzando por la derecha y trabajando hacia la izquierda.

   Usted puede imaginarse el conducir de su coche, el comenzar en el pie del árbol de la decisión y el trasladarse a la derecha a lo largo de las ramificaciones. En cada nodo cuadrado usted tiene control, puede tomar una decisión, y da vuelta a la rueda de su coche. En cada nodo del círculo la señora Fortuna asume el control la rueda, y usted es impotente.

   A continuación se indica una descripción paso a paso de cómo construir un árbol de decisiones:

   1. Dibuje el árbol de decisiones usando cuadrados para representar las decisiones y círculos para representar la incertidumbre.
   2. Evalúe el árbol de decisiones, para verificar que se han incluido todos los resultados posibles.
   3. Calcule los valores del árbol trabajando en retroceso, del lado derecho al izquierdo.
   4. Calcule los valores de los nodos de resultado incierto multiplicando el valor de los resultados por su probabilidad (es decir, los valores esperados).

   Podemos calcular el valor de un nodo del árbol cuando tenemos el valor de todos los nodos que siguen. El valor de un nodo de elección es el valor más alto de todos los nodos que le siguen inmediatamente. El valor de un nodo de probabilidad es el valor esperado de los valores de los nodos que le siguen, usando la probabilidad de los arcos. Retrocediendo en el árbol, desde las ramas hacia la raíz, se puede calcular el valor de todos los nodos, incluida la raíz del árbol. Al poner estos resultados numéricos en el árbol de decisiones obtenemos como resultado el siguiente gráfico:

   
   Arbol de decisiones típicos

   Referencias de la figura
   No Consultant = Sin consultor;
   $500 fee = $500 por honorarios;
   Hire Consultant = Contratar consultor

   Determine la mejor decisión con el árbol partiendo de la raíz y avanzando.

   Del árbol de decisiones surge que nuestra decisión es la siguiente:

   Contratar al consultor y luego aguardar su informe.
   Si el informe predice muchas ventas o ventas medias, entonces producir el producto.
   De lo contrario, no producirlo.

   Verifique la eficiencia del consultor (%) calculando el índice: (Beneficio esperado recurriendo al consultor {monto en $}) / VEIP. El beneficio esperado recurriendo al consultor surge del gráfico como
   BE = 1000 - 500 = 500, mientras que VEIP = 0,2(3000) + 0,5(2000) + 0,3(0) = 1600.
   Por lo tanto, la eficiencia de este consultor es: 500/1600 = 31%

   Como trabajo domiciliario rehaga este problema con distribución previa plana, es decir, trabajando sólo con las recomendaciones de la firma de marketing. Trabajar con distribución previa plana significa que asigna igual probabilidad, a diferencia de (0,2, 0,5, 0,3). Es decir, el dueño del problema no conoce el nivel de ventas si introduce el producto al mercado.

   El Impacto de una Probabilidad Previa y la Matriz de Confiabilidad en sus Decisiones: Para estudiar cuan importante es su conocimiento previo y/ o la precisión de la información esperada de los consultores en sus decisiones, le sugiero que realice de nuevo el ejemplo numérico anterior aplicando análisis de sensibilidad. Usted podría comenzar con el siguiente caso extremo e interesante usando este JavaScript para los cálculos necesarios:

   • Considere una prioridad plana, sin cambiar la matriz de confiabilidad.
   • Considera ana matriz de confiabilidad perfecta (es decir, con una matriz de identidad), sin cambiar la prioridad.
   • Considere una prioridad perfecta, sin cambiar la matriz de confiabilidad.
   • Considera una matriz de confiabilidad plana (es decir, con todos los elementos iguales), sin cambiar la prioridad.
   • Considere la predicción de probabilidades de los consultores como su propia prioridad, sin cambiar la matriz de confiabilidad.

   Diagramas de Influencia: Como puede ser observado en el ejemplo del árbol de decisiones, la descripción de las ramas y nudos el problema de decisiones secuenciales normalmente se hace bastante complicado. En ciertas ocasiones es menos difícil dibujar el árbol de tal forma que preserve las relaciones que realmente manejan las decisiones. La necesidad por mantener la validación, y el rápido incremento en complejidad que usualmente proviene de los usos liberales de las estructuras recursivas, han provisto del proceso de decisiones para describir otros. La razón para esta complejidad es que el actual mecanismo computacional que solía analizar el árbol, esta encarnado directamente dentro de los árboles y las ramas. Las probabilidades y valores requeridos para calcular los valores esperados de las siguientes ramas están expresamente definidos en cada nudo.

   Los Diagramas de Influencia también son utilizados para el desarrollo de modelos de decisión y como una alternativa de representación grafica de árboles de decisión. La figura siguiente muestra un diagrama de influencia para nuestro ejemplo numérico.

   
   
   En el diagrama de influencia anterior, los nudos de decisión y los nudos de oportunidad son ilustrados similarmente con cuadrados y círculos. Los arcos (flechas) implican relaciones, incluyendo probabilísticas.

   Finalmente, el árbol de decisión y el diagrama de influencia proporcionan métodos de tomas de decisiones efectivas porque ellos:

   • Claramente relaja el problema, por lo tanto todas las opciones pueden ser consideradas.
   • Nos permiten ampliamente analizar las posibles consecuencias de una decisión.
   • Proporcionan un esquema para cuantificar los valores delos resultados y las probabilidades para lograr los mismos.
   • Nos ayudan a tomar mejores decisiones basadas en la información existente, así como también hacer mejores adivinanzas.

   También visite:
   Teoría de la Decisión y Árboles de Decision

   ---

   Por que los Gerentes Buscan los Consejos de Firmas Consultores

   Los gerentes le pagan a los consultores para que les proporcionen servicios de asistencia que cae dentro de alguna de las siguientes categorías:

   • El trabajo en el cual no son competentes -- o se sienten que no -- para hacerlo ellos mismos.

   • El trabajo que ellos no quieren hacer.

   • El trabajo que ellos no tienen tiempo para hacerlo por sí mismos.

   Todo tipo de trabajo cae dentro de la amplia sombrilla de trabajos de consultaría. A pesar de las razones del porque los gerentes le pagan a otros para que les den consejos, ellos tienen normalmente expectativas altas en referencia a la calidad de dichas recomendaciones, medidas en términos de confiabilidad y costos. Sin embargo, el gerente es el único responsable por las decisiones tomadas y no el consultor.

   La siguiente figura muestra el proceso para la determinación óptima de la información. Para mas detalles, lea el Análisis de Costo /Beneficio.

   
   La determinación de la Información Optima

   
   

   Decidiendo Acerca de la Firma de Consultores: Cada vez que usted piense en contratar una empresa consultora usted podría enfrentar el peligro de lucir estúpido, sin mencionar la pérdida de miles o hasta millones de dólares. Para empeorar las cosas, la mayoría de las firmas consultoras se han fusionado o se han separado, desaparecido, reaparecido, o reconfigurado por lo menos una vez.

   ¿Como se puede asegurar de elegir la consultora correcta?

   Pruebe el conocimiento que tienen los consultores de su producto. Es importantísimo encontrar en detalles los conocimientos que tienen los consultores potenciales de su producto y del mercado. Haga que la empresa consultora le proporcione un proyecto de plan genérico, lista de trabajos u otros documentos acerca de su producto.

   ¿Existe algún presupuesto o duración de proyecto aprobado?
   ¿Cuál es la expectativa de incorporación clientes potenciales?
   ¿Quién es el encargado de proporcionar la recomendación y firma final esperada?
   

   Inclusive las mejor firmas de consultaría son propensas a tener algunos momentos malos en sus historias de trabajo. Conducir un análisis de confiabilidad es esencial. Hágale a los consultores preguntas específicas en referencia a proyectos anteriores, momentos de orgullo, y esfuerzos fallidos. Por su puesto que es importante también revisar referencias de los consultores. Pregunte por referencias específicas de tantos clientes previos como sea necesario o clientes con negocios relacionados al suyo. Obtenga un contrato claramente escrito, con estimaciones precisas de costos, encuestas estadísticas de tamaño de muestra, y el compromiso de obtener la recomendación escrita a tiempo.

   ---

   Revisando sus Expectativas y su Riesgo

   En nuestro ejemplo, vimos como tomar decisiones basadas en la matriz de redistribución de objetivos mediante el cálculo del valor esperado y del riesgo expresado como coeficiente de variación de nuestros criterios de decisión. Mientras, un tomador de decisiones bien informado pueda estar capacitado a construir su matriz subjetiva de redistribuciones, y luego seguir el mismo proceso de decisión; sin embargo, en muchas situaciones se hace necesario el combinar ambos.

   Aplicación: Suponga que la información siguiente se encuentra disponible de dos fuentes diferentes:

   Revisando el Valor Esoerado y la Varianza
   fuentes de Estimación	Valor Esperado	Varianza
   Sales manager	m1 = 110	s12 = 100
   Encuesta de Mercado	m2 = 70	s22 = 49

   El valor esperado combinado es:

   [m₁/s₁² + m₂/s₂² ] / [1/s₁² + 1/s₂²]

   La varianza combinada es:

   2 / [1/s₁² + 1/s₂²]

   Para nuestra aplicación, usando la información tabular anterior, la estimación combinada de las ventas esperadas es 83,15 unidades con una varianza combinada de 65,77, teniendo un valor de riesgo de 9,6%.

   A usted podría gustarle utilizar el JavaScript de Revisando la Media y la Varianza para realizar algunas experimentaciones numéricas. Usted podría aplicarlo para validar el ejemplo anterior y para entender profundamente los conceptos donde mas de dos fuentes de información son combinadas.

   ---

   Determinación de la función de utilidad del decisor

   Hemos trabajado con tablas de redistribución expresadas en términos del valor monetario esperado. Sin embargo, este no es siempre el mejor criterio de usar en la toma de decisiones. El valor del dinero varia de situación a situación y de una decisión a otra. Generalmente, el valor del dinero no es una función lineal de la cantidad de dinero. En tal caso, el analista debe determinar la utilidad monetaria del tomador de decisiones y seleccionar los cursos de acción que proporcione la utilidad esperada mas elevada, en vez del valor monetario esperado mayor.

   Los pagos individuales de seguros se enfocan en evitar la posibilidad de perdidas financieras asociadas con la ocurrencia de algún evento indeseado. Sin embargo, las utilidades de diferentes resultados no son directamente proporcionales a sus consecuencias monetarias. Si la pérdida es considerada relativamente grande, un individuo es más propenso a pagar una prima asociada. Si un individuo considera que la pérdida no tiene consecuencias, esta persona es más propensa a pagar la prima asociada.

   Las diferencias individuales en actitudes hacia el riesgo y estas diferencias, influenciarán sus opciones. Por lo tanto, individuos deben realizar cada vez la misma decisión con relación al riesgo percibido en situaciones similares. Esto no significa que todos los individuos deberían controlar la misma cantidad de riesgo en situaciones similares. Mas aún, debido a la estabilidad financiera de un individuo, dos individuos enfrentando la misma situación podrían reaccionar de manera diferente a pesar de utilizar los mismos criterios. Una diferencia personal de opinión e interpretación de las políticas también puede producir diferencias.

   La retribución monetaria esperada que se asocia con las diversas decisiones puede no ser razonable por las siguientes dos razones importantes:

   1. El valor en dólares puede no expresar auténticamente el valor personal que el resultado tiene para uno. Esto es lo que motiva a algunas personas a jugar a la lotería por $1.

   2. Si usted acepta los valores monetarios esperados es probable que no esté reflejando con exactitud su aversión al riesgo. Por ejemplo, supongamos que tiene que elegir entre que le paguen $10 por no hacer nada, o participar de una apuesta cuyo resultado depende del lanzamiento de una moneda al aire, pudiendo ganar $1.000 si sale cara y perder $950 si sale cruz. La primera alternativa tiene una recompensa esperada de $10; la segunda tiene una recompensa esperada de 0,5(1000) + 0,5(- 950) = $25, y es claramente preferible a la primera (si la recompensa monetaria esperada fuere un criterio razonable). Pero usted quizás prefiera $10 seguros antes que correr el riesgo de perder $950.

   ¿Por qué algunas personas contratan seguros y otras no? El proceso de toma de decisiones involucra factores psicológicos y económicos, entre otros. El concepto de utilidad es un intento de medir el provecho que tiene el dinero para el decisor en lo individual. Con el concepto de la utilidad podemos explicar por qué, por ejemplo, algunas personas compran billetes de lotería por un dólar para ganar un millón de dólares. Para estas personas, 1.000.000 ($1) es menos que ($1.000.000). Por lo tanto, para tomar una decisión acertada considerando la actitud que tiene el decisor con respecto al riesgo, debemos convertir la matriz de beneficios monetarios en una matriz de utilidad. La principal pregunta sería: ¿Cómo se mide la función de la utilidad con cada decisor?

   Consideremos nuestro Problema de Decisión de Inversión. ¿Cuál sería la utilidad de $12?

   a) Asigne 100 unidades de utilidad y 0 unidades de utilidad al elemento más grande y al más pequeño, respectivamente, de la matriz de beneficios. En nuestro ejemplo numérico, asignamos 100 unidades de utilidad a 15, y 0 unidades de utilidad a -2,

   b) Pídale al decisor que elija entre las siguientes hipótesis:

   Recibir $12 por no hacer nada

   O

   Jugar el siguiente juego: ganar $15 con probabilidad (p) y -$2 con probabilidad (1-p), donde p es un número seleccionado entre 0 y 1.

   Cambiando el valor de p, y repitiendo una pregunta similar, existe un valor de p con el que el decisor es indiferente ante las dos hipótesis. Digamos, p = 0,48.

   c) Ahora, la utilidad para $12 es igual a 0,48(100) + (1-0,48)(0) = 48.

   d) Repita el mismo proceso para hallar las utilidades de cada elemento de la matriz de beneficios. Supongamos que definimos la siguiente matriz de utilidad:

   Matriz de Beneficio Monetario					Matriz de Beneficio de Utilidad
   A	B	C	D		A	B	C	D
   12	8	6	3		48	34	28	13
   15	7	3	-2		100	19	13	0
   7	7	7	7		19	19	19	19

   Ahora se puede aplicar cualquiera de las técnicas antes analizadas a esta matriz de utilidad (en lugar de monetaria) para tomar una decisión satisfactoria. Queda claro que la decisión podría ser diferente.

   Determinación de la función de utilidad del decisor JavaScript E-labs.

   ---

   Representaciones de la Función de Utilidad con Aplicaciones

   Introducción: Una función de utilidad transforma el uso de un resultado en un valor numérico que mide la valoración personal del resultado. La utilidad de un resultado puede estar dentro de una escala comprendida entre 0 y 100, así como hicimos en nuestro ejemplo numérico, convirtiendo la matriz monetaria en una matriz de utilidad . Esta función de utilidad puede ser una simple tabla, un sutil gráfico continuo ascendente, o una expresión matemática de un gráfico.

   El objetivo es representar la función funcional entre las entradas en la matriz monetaria y los resultados obtenidos anteriormente de la matriz de utilidad. Usted podría preguntarse ¿Qué es una función?

   ¿Qué es una función? Una función es algo que hace algo. Por ejemplo, una maquina para moler café es una función que transforma el grano de maíz en polvo. Una función de utilidad transforma (convierte) la esfera de entradas (valores monetarios) hacia un rango de salidas o resultados, con dos valores finales de utilidad 0 y 100. En otras palabras, la función de utilidad determina el grado de sensibilidad de las preferencias del tomador de decisiones.

   Este caítulo presenta un proceso general para determinar la función de utilidad. La presentación esta en el contexto de los resultados numéricos del capítulo anterior, a pesar de que se repiten datos.

   Representación de la Función de Utilidad con Aplicaciones: Existen tres métodos diferentes de representar funciones: el Tabular, el Gráfico, y la Representación Matemática. La selección de un método sobre el otro dependerá de las habilidades matemáticas que tenga el tomador de decisiones de forma tal de entenderlo y usarlo fácilmente. Los tres métodos evolucionan en su procesos de construcción respectivos; por lo tanto, se podría proceder al método siguiente si es preciso.

   La función de utilidad es normalmente usada para predecir la utilidad del tomador de decisiones para un valor monetario dado. La predicción y precisión aumentan desde el método tabular al matemático.

   Representación Tabular de la Función de Utilidad: Podemos tabular los pares de datos (D, U) usando las entradas de la matriz que representan los valores monetarios (D) y sus utilidades correspondientes (U) de la matriz de utilidad obtenida previamente. La forma tabular de la función de utilidad para nuestro ejemplo numérico es dada por la siguiente tabla de pares de datos (D, U):

   Función de Utilidad (U) de la Variable Monetaria (D) en Forma Tabular
   
   

   D 12 8 6 3 15 7 3 -2 7 7 7 7 U 58 34 28 13 100 19 13 0 19 19 19 19

   Representación Tabular de la Función de Utilidad para el Ejemplo Numérico

   Como puede ver, la representación tabular esta limitada a los valores numéricos dentro de la tabla. Suponga que se desea obtener la utilidad en dólares, digamos $10. Se podría usar el método de interpolación; sin embargo, porque la función de utilidad normalmente es no-lineal; el resultado interpolado no representa la utilidad del tomador de decisiones acertadamente. Para enfrentar esta dificultad, se debería usar el método gráfico.

   Representación Grafica de la Función de Utilidad: Se puede dibujar una curva utilizando el diagrama de dispersión obtenido mediante la graficación de los datos en la forma Tabular sobre un papel de gráfico. Ya con el diagrama de dispersión, necesitamos decidir primero la forma de la función de utilidad. El gráfico de utilidad esta caracterizado por sus propiedades de ser sutil, continuo, y curva de forma creciente. Normalmente, una función con forma de parábola se ajusta relativamente bien a las esferas angostas de la variable D. Para esferas más amplias, se podrían ajustar algunas piezas pequeñas de una función de parábola, una para cada sub-esfera apropiada.

   Para nuestro ejemplo numérico, el grafico siguiente es una función sobre el intervalo usado en el modelo de la función de utilidad, dibujado con la utilidad asociada (eje de las U) y el valor asociado en dólares (eje de las D). Note que en el diagrama de dispersión los puntos múltiples están representados por círculos pequeños.

   

   Representación Gráfica de la Función de Utilidad para el Ejemplo Numérico

   La representación gráfica tiene una gran ventaja sobre la tabular y es que se puede leer la utilidad en dólares de $10 directamente del gráfico, como se muestra en la figura anterior para nuestro ejemplo numérico. El resultado es aproximadamente U = 40. Leyendo un valor del gráfico no es conveniente; por lo tanto, para los procesos de predicciones, un modelo matemático es el que mejor funciona.

   Representación Matemática de la Función de Utilidad: Podemos construir un modelo matemático para una función de utilidad utilizando la forma de la función de utilidad obtenida mediante su representación del Método Gráfico. Normalmente, una función con forma de parábola se ajusta relativamente bien a las esferas angostas de la variable D. Para esferas más amplias, se podrían ajustar algunas piezas pequeñas de una función de parábola, una para cada sub-esfera apropiada.

   Sabemos que queremos una función cuadrática que se ajuste mejor al diagrama de dispersión que ha sido construido previamente. Por lo tanto, utilizamos el análsis de regresión para estimar los coeficientes en la función que mejor se ajusta a los pares de datos (D, U).

   Modelos de Parábola: Las regresiones de parábola tienen tres coeficientes con una forma general:

   U = a + bD + cD²,

   donde

   c = { S (D_i - Dbarra)²×U_i - n[S(D_i - Dbarra) ²× SU_i]} / {n S(D_i - Dbarra) ⁴ - [S(D_i - Dbarra)²] ²}

   b = [S(D_i- Dbarra) U_i]/[ S(D_i - Dbarra)²] - 2×c×Dbarra

   a = {SU_i - [c× S(D _i - Dbarra) ²)}/n - (c×Dbarra×Dbarra + b×Dbarra),

   donde Dbarra es la media de D_i's.

   Para nuestro ejemplo numérico i = 1, 2,..., 12. mediante la evaluación de estos coeficientes utilizando la información dada en la sección de la forma tabular, El “mejor” ajuste es caracterizado por sus coeficientes de valores estimados: c = 0,409, b = 0,035, y a = 3,091. El resultado es; por lo tanto, una función de utilidad aproximada por la siguiente función cuadrática:

   U = 0,409D² + 0,035D + 3,091,    para todo D tal que   -2 £ D £ 15.

   La representación matemática anterior proporciona información mas útil que los otros dos métodos. Por ejemplo, colocando D = 10, se obtiene el valor predicho de utilidad U = 44,3. Adicionalmente, tomando la derivada de la función proporciona el valor marginal de la utilidad, por ejemplo,

   Utilidad Marginal = 0,035 + 0,818D,     para todo D tal que   -2 < D < 15.

   Note que para este ejemplo numérico, la utilidad marginal es una función creciente porque la variable D tiene un coeficiente positivo; por lo tanto, se esta capacitado a clasificar esta decisión como un riesgo moderado.

   A usted podría gustarle utilizar el JavaScript de Regresión Cuadrática para comprobar sus cálculos manuales. Para grados mayores que la cuadrática, a usted podría gustarle utilizar el JavaScript de Regresión Polinomial.

   ---

   Una Clasificación de Actitudes Relativas a los Tomadores de Decisiones con Respecto al Riesgo y su Impacto

   Probabilidad de un Evento y el Impacto de su Ocurrencia: El acercamiento de proceso- orientado para manejar el riesgo y la incertidumbre es parte de cualquier modelo probabilístico. Esto le permite al tomador de decisiones examinar el riesgo dentro de su retorno esperado, e identificar aspectos críticos en controlar, limitar y mitigar el riesgo. Este proceso envuelve tanto el aspecto cuantitativo como el cualitativo de controlar el impacto del riesgo.

   La teoría de la decisión no describe lo que las personas hacen dado que existen dificultades con los cálculos de probabilidad y la utilidad de los resultados. Las decisiones también pueden estar afectadas por la racionalidad subjetiva de las personas y por la manera en la cual el problema de decisión es percibido.

   Tradicionalmente, el valor esperado de una variable aleatoria ha sido usado como la mejor ayuda para cuantificar el monto del riesgo. Sin embargo, el valor esperado en solitario no es necesariamente una buena medida por la cual tomar decisiones porque no hace clara la distinción entre probabilidad y severidad. Para demostrarlo, considere el siguiente ejemplo:

   Suponga que una persona debe escoger entre dos escenarios 1 y 2 mostrados a continuación:

   • Escenario 1: Existe 50% de posibilidad de perder $50, y 50% de que no.

   • Escenario 2: existe 1% de posibilidad de perder $25, y 99% de que no.

   Ambos escenarios resultan en una perdida esperada de $25, pero esto no refleja el hecho de que el escenario 2 podría considerarse mas riesgoso que el primero. (Por supuesto, este es un control subjetivo) El tomador de decisiones podría estar mas preocupado sobre minimizar el efecto de ocurrencia de un evento extremo en vez de preocuparse por la media. El cuadro siguiente muestra la complejidad de la probabilidad de un evento, el impacto de la ocurrencia del mismo, y su indicador de riesgo asociado respectivamente:

   

   

   De la sección previa se podría recordar que la certeza equivalente es la rentabilidad libre de riesgo. Adicionalmente, la diferencia entre la certeza que posea un tomador de decisiones y el valor monetario esperado (VME) es llamado prima de riesgo. Deberíamos usar el signo y la magnitud de la prima de riesgo en la clasificación de la actitud relativa del tomador de decisiones hacia el riesgo como sigue a continuación:

   • Si la prima de riesgo es positiva, el tomador de decisiones esta deseando tomar riesgo, por lo cual se le llama buscador de riesgo. Obviamente, unas personas aceptan mas riesgo que otras; mientras mas alta sea la prima de riesgo, mas riesgo es aceptado por el tomador de decisiones.

   • Si la prima de riesgo es negativa, el tomador de decisiones evitará tomar riegos por lo cual se le llama adverso al riesgo.

   • Si la prima de riesgo es cero, el tomador de decisiones se le llama riesgo neutral.

   ---

   El Descubrimiento y la Gerencia de las Pérdidas

   En el descubrimiento y gerencia de las pérdidas (expresado en términos monetarios), la percepción y la medición de la posibilidad de un evento son crucial. Las perdidas podrían tener varias fuentes. Estas fuentes incluyen Empleados, Procedimientos, y Factores Externos.

   • Empleados: Algunos empleados podrían tener problemas de concentración, conocimientos insuficientes, y estar envueltos en fraudes.
   • Procedimientos: Algunos procedimientos están erróneamente diseñados, o son erróneamente implementados.
   • factores Externos: Estos incluyen la dependencia de servicios y suplidores externos desconfiables, falta de seguridad para actividades criminales externas, y finalmente desastres naturales tales como terremotos.

   Un evento raro o inesperado con consecuencias potencialmente significativas para el tomador de decisiones podrían ser concebidas como riesgos o como oportunidades. Las preocupaciones principales son: ¿Cómo preparase para controlarlos?

   Un tomador de decisiones conectado a la planificación, necesita adoptar una posición hacia el futuro de forma de decidir los objetivos, y decidir cual es la mejor secuencia de acciones para conseguir dichos mediante el pronóstico de sus consecuencias. Desafortunadamente, la desconexión de dichos eventos hace difícil su predicción o explicación por métodos que usan datos históricos. Sin embargo, se debe enfocar en los factores de la actitud psicológica del tomador de decisiones y en su entorno mas relevante.

   La figura siguiente proporciona una clasificación de la función de frecuencia de perdidas junto a los rangos Esperados, Inesperados y el Stress, los cuales deben ser determinados por la habilidad del tomador de decisiones y los recursos disponibles.

   

   La habilidad del gerente para descubrir tanto los eventos de perdidas inesperadas y de stress y pronosticar sus consecuencias es la mayor tarea. Esto ocurre porque estos eventos son poco probables; por lo tanto difíciles de predecir y explicar. Sin embargo, una vez que el evento raro ha sido identificado, la preocupación principal es las consecuencias para la organización. Un buen gerente no puede ignorar estos eventos, porque sus consecuencias son significativas. Por ejemplo, a pesar de que un fuerte terremoto ocurre raramente en las más grandes centros urbanos, raramente tienen consecuencias en términos económicos y humanos mas allá del tremor típico. Un cuerpo de seguridad publica racional para una ciudad en un terremoto planearía un plan de contingencia a pesar de que la posibilidad de ocurrencia de un terremoto fuerte sea muy pequeña.

   ---

   Evaluación del riesgo: ¿Cuán acertada es su decisión?

   El riesgo es la inconveniencia de una apuesta, la cual es descrita en términos de probabilidad. El control de riesgo es un procedimiento de cuantificación de los valores de pérdida o ganancia y proporcionarlos con apropiados valores de probabilidad. En otras palabras, el control de riesgo significa construir la variable aleatoria que describe el riesgo. El indicador de riesgo es una cantidad describiendo la calidad de la decisión.

   Considerando nuestro Problema de Decisión de Inversión:

   		Estados de la Naturaleza
   		Crecimiento	Crec. medio	Sin cambio	Bajo
   		C	CM	SC	B
   	Bonos	12%	8	6	3
   Cursos de acción	Acciones	15	7	3	-2
   	Depósito	7	7	7	7

   Los estados de la naturaleza son los estados de la economía durante, digamos, un año. El Valor Esperado (es decir, promedios):

   Valor esperado = å x _i . P(x _i)

   por sí solo no indica adecuadamente que la decisión es de calidad acertada. Se necesita saber la varianza para tomar una decisión educada. ¿Alguna vez les contaron del dilema del estadístico que medía 1,80 metros y se ahogó en un arroyo que tenía 90 cm de profundidad promedio?

   En nuestro ejemplo numérico también nos interesa el "riesgo" comparativo entre los cursos de acción alternativos. Una de las medidas del riesgo en general se expresa como variación, o su raíz cuadrada, llamada desviación estándar. La variación, o la desviación estándar, son valores numéricos que indican la variabilidad inherente a la decisión. Si el valor del riesgo es más bajo indica que lo que usted esperaba obtener es más probable. Por lo tanto, el riesgo también podría usarse para comparar cursos de acción alternativos. Lo que deseamos es un mayor retorno esperado con menor riesgo. Es por ello que al gerente le preocupa tanto el alto riesgo.

   Varianza: Una medida importante del riesgo es la varianza.

   Varianza = [åx_i . x _i . P(x_i)] -
   (Valor esperado)²

   La varianza es una medida del riesgo; por lo tanto, cuanto mayor la varianza, mayor el riesgo. La varianza no se expresa en las mismas unidades que el valor esperado (digamos, en $). En otras palabras, la varianza es difícil de entender y explicar porque es el término al cuadrado de su cálculo. Este problema puede resolverse trabajando con la raíz cuadrada de la varianza, llamada desviación estándar.

   Desviación estándar = (Varianza) ^1/2

   Ambas, la varianza y la desviación estándar, proporcionan la misma información; siempre se puede obtener una de la otra. En otras palabras, el proceso de calcular una desviación estándar siempre involucra el cálculo de una varianza. Como la desviación estándar es la raíz cuadrada de la varianza, siempre se expresa en las mismas unidades que el valor esperado.

   Ahora, la pregunta es "¿qué curso de acción tomar entre uno que tiene un resultado esperado mayor y otro, con resultado esperado menor pero riesgo mucho mayor?" Para tomar una decisión acertada en estos casos, se puede usar otra medida de riesgo, conocida como el Coeficiente de Variación. El Coeficiente de Variación (C.V.) es el riesgo relativo con respecto al Valor Esperado, que se define como:

   El Coeficiente de Variación (CV) =
   (Desviación estándar / Valor esperado)100 %

   Observe que el CV es independiente de la medida de unidad de valor esperado. La inversa de CV (es decir, 1/CV) se llama Relación Señal/ Ruido. El coeficiente de variación se usa para representar la relación entre la desviación estándar y el valor esperado; expresa el riesgo como porcentaje del valor esperado.

   Puede calcular la calidad de su decisión usando la calculadora Media, Desviación Estándar, Calculador CV.

   La siguiente tabla muestra las mediciones de riesgo calculadas para el Problema de Decisión de Inversión:

   										Evaluación del	riesgo
   	C (0,4)		CM (0,2)		SC (0,3)		B (0,1)		Valor esperado	Desviación estándar	C. V.
   Bonos	12		8		6		3		8,5	3,12	37%
   Acciones	15		7		3		-2		8,1	6,11	75%
   Depósito	7		7		7		7		7	0	0%

   De las columnas de Evaluación del Riesgo en la tabla se llega a la conclusión de que los Bonos son mucho menos riesgosos que las Acciones. Es claro que el Depósito está exento de riesgo. Ahora, la última pregunta es: Con toda la información relevante, ¿qué curso de acción asumir? Todo depende de usted.

   Yo no sé nada: Todos los estados de la naturaleza tienen igual probabilidad. Como yo no sé nada sobre la naturaleza, todo es igualmente probable (Laplace):

   										Evaluación del	riesgo
   	C (0,25)		CM (0,25)		SC (0,25)		B (0,25)		Valor esperado	Desviación estándar	C. V.
   Bonos	12		8		6		3		7.25	3.27	45%
   Acciones	15		7		3		-2		5.75	6.22	108%
   Depósito	7		7		7		7		7	0	0%

   De las columnas de Evaluación del Riesgo en la tabla se llega a la conclusión de que los Bonos son mucho menos riesgosos que las Acciones. Es claro que el Depósito está exento de riesgo. Ahora, la última pregunta es: Con toda la información relevante, ¿qué curso de acción asumir? Todo depende de usted.

   Proceso de Ranking para la Preferencia entre Alternativas: Refiriéndonos a las alternativas de los Bonos y las Acciones en nuestro ejemplo numérico, notamos basado en la media- varianza, la alternativa de los Bonos domina a la de las Acciones. Sin embargo, este no es siempre el caso. Por ejemplo, considere dos alternativas de inversión: Inversión I e Inversión II con sus características resumidas en la siguiente tabla:

   Dos Carteras de Inversión
   Inversión I			Inversión II
   Rentabilidad %	Prob.		Rentabilidad %	Prob.
   1	0,25		3	0,33
   7	0,50		5	0,33
   12	0,25		8	0,34

   Comportamiento de Dos Inversiones

   Para clasificar estas dos inversiones bajo la Aproximación de la Dominación Estándar en Finanzas, tenemos que calcular primero la media y la desviación estándar y luego analizar los resultados. Usando el Applet anterior para los cálculos, nos damos cuenta que la inversión I tiene una media de 6,75% y una desviación estándar de 3,9%, mientras que la inversión II tiene media 5,36% y una desviación estándar de 2,06%. Observe primero que bajo el análisis usual de media-varianza, estas dos inversiones no pueden ser clasificadas. Esto ocurre porque la inversión I tiene la media y la desviación estándar más grande. Por lo tanto la Aproximación de la Dominación Estándar no es útil aquí. Debemos re-ordenar el coeficiente de variación (CV) como una base sistemática de comparación. El CV para la inversión I es 57,74% y para la inversión II 38,43%. Por lo tanto, la inversión II tiene la preferencia sobre la otra. Claramente, este acercamiento puede ser utilizado para clasificar cualquier numero de alternativas de inversión.

   Como otra aplicación, considere una inversión de $10000 sobre un período de 4 años que retorna T(t) al final del año t, con R(t) siendo estadísticamente independiente como sigue:

   R(t)	Probabilidad
   $2000	0,1
   $3000	0,2
   $4000	0,3
   $5000	0,4

   ¿Es esta una inversión atractiva dado que la tasa atractiva mínima de retorno (TAMR) es I =20%?

   Se podría calcular el retorno esperado: E[R(t)] = 2000(0,1) +….= $4000

   Sin embargo el valor presente, usando el factor de descuento [(1+I)ⁿ -1]/[I(1+I)ⁿ] = 2,5887, n=4, para la inversión es:
   4000(2,5887) - 10000 = $354,80.

   Nada mal. Sin embargo, se necesita saber su riesgo asociado. La varianza de R(t) es:
   Var[R(t)] = E[R(t)²] - {E[R(t)]}² = $²10⁶.
   Por lo tanto, su desviación estándar es $1000.

   Una medida mas apropiada es la varianza del valor presente, la cual es:
   Var(PV) = S Var[R(t)]. (1+I)^-2t = 106 [0,6944+…+0,2326] = 1,7442(10⁶),
   por lo tanto, su desviación estándar es $1320,68.

   ¿Desea invertir?

   La diversificación podría reducir su riesgo: Diversificando su decisión podría reducir su riesgo sin reducir los beneficios de las ganancias sus actividades. Por ejemplo, usted podría escoger el comprar una variedad de acciones en vez de un solo tipo utilizando el ranking del coeficiente de variación.

   Capturando el Riesgo

   • Evitar el riesgo es rehusarse a tomar una actividad donde el riesgo se ve muy cerca.
   • La prevención de riesgo (control de pérdidas) es usar varios métodos para reducir la posibilidad de que la pérdida.
   • La transferencia del riesgo es la cesión del riesgo a otra persona fuera de su compañía.
   • Asumir el riesgo o auto-asegurarse es colocar fondos para enfrentar pérdidas que son son inciertas en tamaño y frecuencia.

   

   ---

   Implementaciones de computación para Modelos de Análisis de Decisiones: WinQSB

   El módulo Da.exe "Decision Analysis" del paquete WinQSB se usa para dos propósitos diferentes: para resolver problemas grandes y para realizar experimentaciones numéricas, tales como análisis "what if" (o de supuestos) con la matriz de beneficios y las asignaciones de probabilidades subjetivas con los estados de la naturaleza.

   Bayesian Analysis (Análisis de Bayesiano): Seleccione esta opción en la pantalla Problem Specification (Especificación del Problema) para entrar las probabilidades a priori y las probabilidades condicionales (la probabilidad de un valor de indicador dado un estado de la naturaleza). Luego pulse el ícono "solve" para obtener las probabilidades a posteriori.

   Arboles de decisiones: Primero debe dibujar el árbol de decisiones para luego poder numerar todos los nodos, incluidos los nodos terminales. Estos números son la identificación de los nodos cuando se construye el árbol de decisiones en el programa.

   Cuando esté listo para entrar los datos seleccione la opción "Decision Tree Analysis" en la pantalla "Problem Specification".

   Para cada nodo debe identificar los nodos que están inmediatamente conectados (escriba <número de nodo>,…, <número de nodo>).

   Corrija los errores escribiendo directamente los cambios en las celdas apropiadas.

   ---

   Una selección de:

   |Associação Portuguesa de Investigação Operacional| BUBL Catalogue| Ciencias Sociales| Decision Modeling| Decision Sciences Institute| Economía| Excite: Operations Research| Gacetilla Matemática| La Brujula S.A.| MERLOT| |NetFirst| OpenHere: Mathematics| Scottish Further Education| Scout Report |Society for Judgment and Decision Making |Society for Medical Decision Making |toma de decisiones |Virtual Library | World Lecture Hall |Yahoo|

   Pueden encontrarse más sitios haciendo clic en los siguientes motores de búsqueda:

   ---

   Declaración de derechos de propiedad intelectual: El uso legítimo, según las pautas de 1994 guías de consulta justas del uso para los multimedia educativos, de los materiales presentados en este sitio Web está permitido para propósitos educativos no comerciales.
   Este sitio puede duplicarse, intacto con esta declaración, en cualquier servidor de acceso público y puede vincularse a cualquier otra página Web. Todos los archivos se encuentran disponibles en http://www.mirrorservice.org/sites/home.ubalt.edu/ntsbarsh/Business-stat para el duplicado.

   Agradecería recibir comentarios, sugerencias e inquietudes por e-mail. Gracias.

   Profesor Hossein Arsham   

   ---

   Este sitio fue lanzado el 25/2/1996, y sus materiales intelectuales son revisados a fondo anualmente. La versión actual es la 8^a Edición. Todos los links externos son chequeados una vez al mes.

   ---

   Vuelta a:

   Ciencia de la Administración Aplicada para Gerentes y Lideres Gerenciales,
   Sitio Espejo para España,  Sitio Espejo para América Latina

   Modelos Deterministas: Optimización lineal,
   Sitio Espejo para España,  Sitio Espejo para América Latina.

   Optimización de Enteros y Modelos de Redes,
   Sitio Espejo para España,  Sitio Espejo para América Latina.

   Introducción a la Teoría de Juegos ,
   Sitio Espejo para España,  Sitio Espejo para América Latina.

   Toma de Decisiones con Periodos de Tiempo Crítico en Economía y Finanzas,  
   Sitio Espejo para España,  Sitio Espejo para América Latina.

   Razonamiento Estadístico para la Toma de Decisiones Gerenciales,  
   Sitio Espejo para España,  Sitio Espejo para América Latina.

   Una Clasificación de JavaScript Estadíticos,  
   Sitio Espejo para España,  Sitio Espejo para América Latina.

   El Aprendizaje con la Asistencia del Computador,
   Sitio Espejo para España,  Sitio Espejo para América Latina.

   Temas en Algebra Lineal,
   Sitio Espejo para España,  Sitio Espejo para América Latina.

   Construcción de Regiones de Sensibilidad General de Programación Lineal,
   Sitio Espejo para España,  Sitio Espejo para América Latina.

   ---

   EOF: Ó 1994-2015.

   ---