Introduction
Unlike the ordinary sensitivity analysis, the construction presented here allows us for any dependent, independent, multiple changes in both the RHS values and the cost coefficients of linear program models having unique solution.
One may tackle uncertainties in a more "deterministic" manner. The approach is called various names such as "scenario modeling", "deterministic modeling", "sensitivity analysis", and "stability analysis". The idea is to subjectively come up with a ranked list of higher level uncertainties that might presumably have a bigger impact on the eventual mapping result. This is done before zooming in on the details of any particular "scenario" or model.
An understanding of the influence of the above on the course of action suggested by the model is crucial because:
Different levels of acceptance (by the general public, by the decision-makers, by stakeholders) may be attached to different types of uncertainty.
Different uncertainties impact differently on the reliability, robustness, and efficiency of the construct.
The relevance of the construct (its appropriateness to the task) strongly depends on the impact of uncertainty on the outcome of the analysis. Surprise is not an element of a robust optimal decision.
Examples of settings where the above applies are many, and include:
- Construction of e.g., economic and environmental indicators
- Analysis and forecast of risk with applications in environmental, financial, and insurance-risk
- Model optimization and calibration
Why Sensitivity Analysis?
The following is a condensed list of reasons why sensitivity analysis should be considered:Decision making or development of recommendations for decision makers
Testing the robustness of an optimal solution. Surprise is not an element of a robust optimal decision.
Identifying critical values, thresholds, or breaking-even values where the optimal strategy changes.
Identifying sensitivity, i.e., important parameters, e.g., in Elasticity applications.
Investigating sub-optimal solutions.
Developing flexible recommendations that depend on the circumstances.
Comparing the values of simple and complex decision strategies.
Assessing the "risky-ness" of a strategy or scenario.
Communication
Making recommendations more credible, understandable, compelling, or persuasive.
Allowing decision makers to select assumptions.
Conveying a lack of commitment to any single strategy.
The decision maker might incorporate some other perspectives of the problem such as cultural, political, psychological, etc., into the management scientist's recommendations.
Increase Understanding or qualification of the system
Estimating relationship between parameters and the output.
Understanding relationship between input and output variables.
Developing hypotheses testing.
Model development
Testing the model for validity or accuracy.
Searching for errors in the model
Simplifying the model.
Calibrating the model.
Coping with poor or missing data.
Prioritizing acquisition of information.
Condensed list of instances where sensitivity analysis should be considered:
- With controlling the problems, SA may help to identify critical regions in the space of the input parameters.
- In screening exercises, SA may help to locate a few influential parameters in systems with hundreds of uncertain inputs.
- Variance based SA techniques are useful to ascertain if a subset of input parameters may account for (most of) the output variance.
- Point (3) above may be used for mechanism reduction (dropping or fixing non relevant parts of the model) and for model lumping (building/extracting a model from a more complex one). See also the problem of model "relevance": are the parameters in the model input set relevant to the task of the model?
- Point (3) above may also be used for model identification by pinpointing the experimental conditions for which your ability to discriminate among the model is at maximum.
- As in (5) above, SA may be used for model calibration, to ascertain if the experiments with its related uncertainties will allow parameter estimation. This is especially useful against ill-conditioned (formulated) problems.
- SA may be coupled to optimization / search algorithms; by identifying the most important parameters, SA may allow the dimensionality of the space where the search is made to be reduced.
- As a quality assurance tool, SA makes sure that the dependence of the output from the input parameters in the model has a physical resemblance and explanation.
- To solve an inverse problem, SA serves as a tool to extract parameters embedded into models whose output does not correlate easily with the unknown input (e.g., in chemical kinetics, to extract kinetic constants of complex systems from the measured yield rate of components.
- To optimally allocate resources in R&D, SA shows where it is more worthwhile to invest in order to reduce the model's range of uncertainty.
- SA can ascertain on a quantitative basis what fraction of my prediction uncertainty is due to parametric estimation uncertainty and how much to structural uncertainty.
Dealing With the Uncertainty
The Current approaches to deal with uncertainties includes:Scenario Analysis: In this approach one assumes scenarios (e.g. certain combinations of possible values of uncertain parameter) and solves the problem for each. By solving the problem repeatedly for different scenarios and studying the solutions obtained, the manager observes sensitivities and heuristically decides on an approximate, which is subjective.
Worst-case Analysis: This technique attempts to account for putting safety margins into the problem in the planning stage.
Monte-Carlo Approach: Stochastic models assume that the uncertainty in is known by its statistical distribution.
A Classification of Sensitivity Analysis Activites
Unlike the ordinary sensitivity analysis, the construction presented here allows us for any dependent, independent, multiple changes in both the RHS values and the cost coefficients as shown in the following Figure. The computations evolve some elementary matrix manipulations.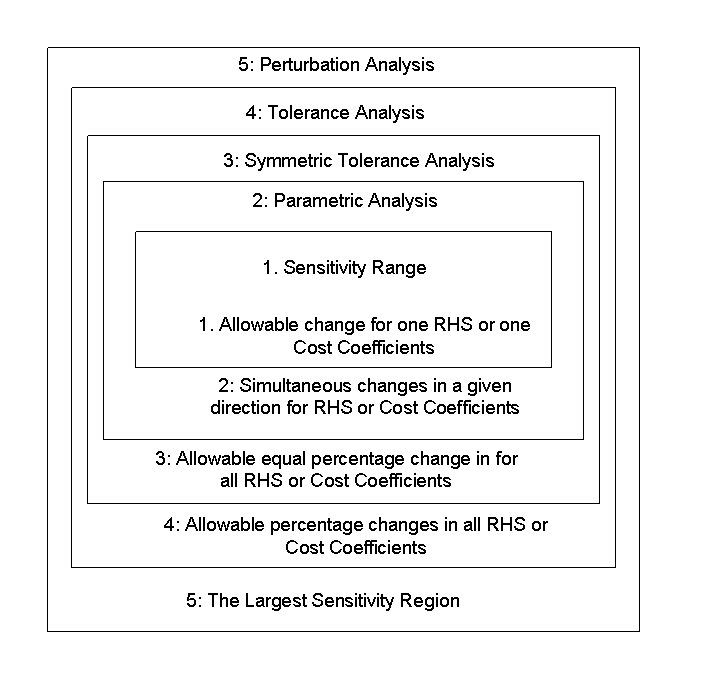
Click on the image to enlarge it and THEN print it.
The Genealogy of Various Sensitivity Analysis Activities with their Limitations
Given the outcome of a linear program formulation and calculation for the solution a series of analysis can provide valuable management information to deal with uncertainties. These uncertainty ranges can be obtained by performing the following different types of sensitivity analysis depending on the nature of the uncertainty: perturbation analysis; tolerance analysis; individual symmetric tolerance analysis; symmetric tolerance analysis; parametric sensitivity analysis; and ordinary sensitivity analysis.
Perturbation Analysis: Simultaneous and independent changes in the any parameter in either direction (over or under estimation) for each parameter that maintain the optimal basis. This provides the largest set of perturbations.
Tolerance Analysis: Simultaneous and independent changes expressed as the maximum allowable percentage of the parameter's value in either direction (over or under estimation) for each parameter that maintains the optimal basis. This provides a range of values for each parameter.
Individual Symmetric Tolerance Analysis: Simultaneous and independent equal changes expressed as the maximum allowable percentage of the parameters' value in both directions (over and under estimation) for each parameter that maintains the optimal basis. This provides a range of values for each parameter with the current value at its center.
Symmetric Tolerance Analysis: Simultaneous and independent equal changes expressed as maximum allowable percentage of the parameter's value in both directions (over and under estimation) for all activity that maintain the optimal basis. This provides one single range of values of uncertainty for all parameters.
Parametric Analysis: Simultaneous changes of dependent parameter values from their nominal values that maintain the optimal basis. This provides the maximum magnitude of change for values of dependent parameters.
Ordinary Sensitivity Analysis: One change-at-a-time in any parameter value that maintains the optimal basis. This provides a range for the change of any specific parameter value, holding all others at their nominal values.
In performing the above various type of sensitivity analysis, the needed computations are some elementary matrix manipulations of the readily available tools for construction of the sensitivity region.
Tools for Construction of the Sensitivity Region
Referring to the Carpenter's Problem, for small changes in either resources the optimal strategy (i.e.; make the mixed-product) stays valid. For larger changes this optimal strategy moves and the Carpenter must either make All the tables Or the chairs he/she can. This is a drastic change in the strategy, therefore, we have to revise the formulation and solve a new problem.Apart from the above needed information, we are also interested to know how much the Carpenter can sell (or buy) each resources at a Reasonable price (or cost). That is, how far can we increase or decrease RHS(i), for fixed i while maintaining the validity of current shadow price of the RHS(i)? That is, how far can we increase or decrease RHS(i), for fixed i while maintaining the current optimal solution to The Dual Problem?
Historically, the shadow price was defined as the improvement in the objective function value per unit increase in the right hand side, because the problem were often put in the form of profit maximization improvement meant increase.
Know also that, for any RHS, the shadow price (known also, as its marginal value), is the amount of change in the optimal value proportion to one unit change for that particular RHS. However, in some cases it is not permitted to change the RHS by that much. The sensitivity range for the RHS provides the values for which the shadow price has such an economic meaning, and remains unchanged.
As part of post-optimal solution, we are interested in finding sensitivity ranges for the RHS values, and coefficients of the objective function.
All the tools we need to perform sensitivity analysis are readily available in the simplex final table. The first column of this table contains the basic variable vector whose optimal value is contained in the last column called the RHS column vector. The body of the table contains and identity matrix corresponding to the basic variables and the non-basic variables matrix denoted by BNB. The last row of this table called the Cj row.
Numerical Example 1: Consider the following LP problem, we shall refer to as the Carpenter's Problem:
Max 5 X1 + 3 X2
Subject to:
2 X1 + X2 £ 40 labor constraint
X1 + 2 X2 £ 50 material constraint
and both X1, X2 are non-negative.
Introducing slack variables for converting the constraints into equality form, we have:
Max 5 X1 + 3 X2
Subject to:
2 X1 + X2 + S1 = 40
X1 + 2 X2 + S2 = 50
all variables are non-negative.
The Sensitivity Analysis Tools: The following sensitivity analysis tools are also obtainable by using the Linear Optimization with Sensitivity Analysis Tools JavaScript.
| S1 | S2 | |
|---|---|---|
| 2/3 | -1/3 | |
| -1/3 | 2/3 |
| X1 | X2 | S1 | S2 | |
|---|---|---|---|---|
| 0 | 0 | -7/3 | -1/3 |
The elements of Cj correspond to the Decision Variables in the same sequence as they appeared in the objective function, then followed by the Slacks/Surplus Variables. The Cj element for the Basic Variables is always equal to zero.
Notice that number of zero elements in the Cj row vector must be equal to the number of constraints, otherwise the problem might have multiple solutions, and therefore any sensitivity analysis results could be misleading.
Note that the shadow price of the ith RHS is equal to minus one times the element of Cj vector at the Si column. For this numerical example the shadow price U1 and U2 of the first and second RHS values (50, and 50), are U1 = (-1)(-7/3) = $7/3 and U2 = (-1)(-1/3) = $1/3. Clearly, this is also the optimal solution strategy for The Dual Problem.
| RHS | |
|---|---|
| 10 | |
| 20 |
The elements of RHS are the Basic Variables value. Moreover, they are always non-negative. The the optimal value of all non-basic variables is always equal to zero.
Notice that if any element in the RHS vector column is zero, then the optimal solution could be a degenerate solution, therefore any sensitivity analysis results could be misleading.
Construction of the Optimal Simplex Tableau: The first row of the simplex optimal tableau contains the decision variable names in the same order, as they appeared in the objective function, followed by the slacks/surplus variable corresponding to the order f the constraints. The rest of elements in the optimal tableau can be filled-in by the Linear Optimization with Sensitivity Analysis Tools JavaScript.
The optimal simplex tableau for this problem is:
| BVS | X1 | X2 | S1 | S2 | RHS | |
|---|---|---|---|---|---|---|
| X1 | 1 | 0 | 2/3 | -1/3 | 10 | |
| X2 | 0 | 1 | -1/3 | 2/3 | 20 | |
| Cj | 0 | 0 | -7/3 | -1/3 |
Sensitivity of the Constraints' Right-hand-side Values:
The shadow prices remain unchanged
In this section, we are interested to find out under what conditions the current marginal values' of the RHS values of the constraints remain unchanged
Numerical Example 2: Consider the following LP problem:
Max -X1 + 2X2
subject to:
X1 + X2 ³ 2,
-X1 + X2 ³ 1,
X2 £ 3,
and X1, X2 ³ 0.
Introducing slack/surplus variables for converting the constraints into equality form, we have:
X1 + X2 - S1 = 2,
-X1 + X2 - S2 = 1,
X2 + S3 = 3,
and all variables are non-negative.
The optimal tableau for this problem is:
| BVS | X1 | X2 | S1 | S2 | S3 | RHS | |
|---|---|---|---|---|---|---|---|
| S2 | 1 | 0 | 0 | 1 | 1 | 2 | |
| X2 | 0 | 1 | 0 | 0 | 1 | 3 | |
| S1 | -1 | 0 | 1 | 0 | 1 | 1 | |
| Cj | -1 | 0 | 0 | 0 | -2 |
Consider changing the RHS(1) from 2 to 2 + r1. The parametric RHS for the optimal tableau is the current RHS in the optimal tableau plus (if the constraint is £), and minus (if the constraint is ³) column of S(i) times r1.
2 - (0). r1
3 - (0). r1
1 - (1). r1
To maintain feasibility, all elements of parametric RHS must be non-negative. This gives:
1 - r1 ³ 0, that is r1 £ 1. Therefore, the amount of allowable increase is 1, and allowable decrease is as much as you want.
Similarly, for RHS(2)= 1, changing to 1 + r2, the parametric RHS in the optimal tableau is:
2 - (1). r2
3 - (0). r2
1 - (0). r2
This gives 2-r2 ³ 0, that is r2 £ 2. Therefore, the amount of allowable increase is 2, and allowable decrease is as much as you want.
For the RHS(3)=3, changing it to 3 + r3, the parametric RHS is:
2 + (1). r3
3 + (1). r3
1 + (1). r3
Setting all elements to ³ 0, give r3 ³ -1. Thus the allowable decrease is 1, while allowable increase is as much as you want.
Notice that, the parametric optimal value with r3 as its parameter is: -X1 + 2X2 = 0 + 2 (3 + r3) = 6 + 2r3. By substituting r3 = 0, this gives the optimal value. Notice also that, the coefficient of r3 in the parametric optimal value is 2 which is the shadow price of the RHS of the 3rd constraint, this observation is always true. That is why, we stated early that, the shadow price (marginal value), is the amount of change in the optimal value proportion to one unit change for that particular RHS.
Although we restrict our discussion on one RHS change at a time, in the above example, one may extend it to the case of multiple RHS changes simultaneously, this is done in the following application.
Numerical Example 3: As our numerical example for multiple RHS changes simultaneously, consider the Carpenter's Problem:
Maximize 5 X1 + 3 X2
Subject to:
2 X1 + X2 £ 40 labor constraint
X1 + 2 X2 £ 50 material constraint
and both X1, X2 are non-negative.
The optimal simplex tableau for this problem is:
| BVS | X1 | X2 | S1 | S2 | RHS | |
|---|---|---|---|---|---|---|
| X1 | 1 | 0 | 2/3 | -1/3 | 10 | |
| X2 | 0 | 1 | -1/3 | 2/3 | 20 | |
| Cj | 0 | 0 | -7/3 | -1/3 |
Now consider, the parametric RHS version of this problem:
Maximize 5 X1 + 3 X2
Subject to:
2 X1 + X2 £ 40 + r1
X1 + 2 X2 £ 50 + r2
and both X1, X2 are non-negative.
Following the same procedure but perturbing both RHS's by r1, and r2 respectively, using the columns of slack/surplus of the optimal tableau, one obtains the following parametric RHS's, directly.
| BVS | X1 | X2 | S1 | S2 | Parametric RHS | |
|---|---|---|---|---|---|---|
| X1 | 1 | 0 | 2/3 | -1/3 | 10 + 2r1/3 -r2/3 | |
| X2 | 0 | 1 | -1/3 | 2/3 | 20-r1/3 + 2r2/3 | |
| Cj | 0 | 0 | -7/3 | -1/3 |
Note that by perturbing both RHS's by r1, and r2 respectively, one obtains the general sensitivity region for simultaneous, independent (or dependent) changes in both RHS's as follow:
The following, region depicts the general sensitivity analysis for the RHS's values of the Carpenter's Problem:
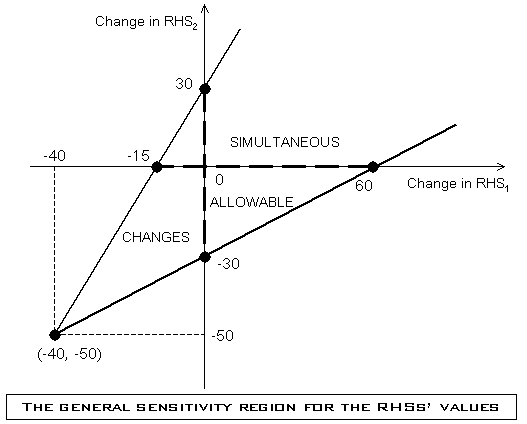
Click on the image to enlarge it and THEN print it.
General Sensitivity Region for RHS's Values
Notice that, the sensitivity region contains the origin which corresponds to the nominal problem. Furthermore the vertex of the sensitivity region is at the point (-40, -50) where both RHS's vanish.
Analyzing the LP Models with Equality Constraints
Numerical Example 4: Consider the following LP problem with an equality constraint:
Max 5X1 + 3X2
Subject to:
2X1 + X2 £ 40
X1 + X2 = 26
and both X1, X2 are non-negative.
Converting the equality constraints to two inequality constraints, we have the following equivalent problem:
Max 5X1+ 3X2
Subject to:
2X1 + X2 £ 40
X1 + X2 £ 26
X1 + X2 ³ 26
and X1, X2 ³ 0.
Introducing slack/surplus variables for converting the constraints into equality form, we have:
Max 5X1+ 3X2
Subject to:
2X1 + X2 + S1 = 40
X1 + X2 + S2 = 26
X1 + X2 - S3 = 26
and all variables are non-negative.
The Sensitivity Analysis Tools: The following sensitivity analysis tools are also obtainable by using the Linear Optimization with Sensitivity Analysis Tools JavaScript.
| S1 | S2 | |
|---|---|---|
| 1 | -1 | |
| 0 | 1 | |
| -1 | 2 |
| X1 | X2 | S1 | S2 | S3 | |
|---|---|---|---|---|---|
| 0 | 0 | -2 | -1 | 0 |
The elements of Cj correspond to the Decision Variables in the same sequence as they appeared in the objective function, then followed by the Slacks/Surplus Variables. The Cj element for the Basic Variables is always equal to zero.
Notice that number of zero elements in the Cj row vector must be equal to the number of constraints, otherwise the problem might have multiple solutions, and therefore any sensitivity analysis results could be misleading.
| RHS | |
|---|---|
| 14 | |
| 0 | |
| 12 |
The elements of RHS are the Basic Variables value. Notice that if any element in the RHS vector column is zero, then the optimal solution could be a degenerate solution, therefore any sensitivity analysis results could be misleading.
Therefore, the optimal tableau with parametric RHS for this problem is:
| BVS | X1 | X2 | S1 | S2 | S3 | Parametric RHS | ||
|---|---|---|---|---|---|---|---|---|
| X1 | 1 | 0 | 1 | -1 | 0 | 14 + (1)r1+ (-1 - 0)r2 | = 14 + r1 - r2 | |
| S3 | 0 | 0 | 0 | 1 | 1 | 0 + 0r1 + (1 - 1)r2 | = 0 | |
| X2 | 0 | 1 | -1 | 2 | 0 | 12 + (-1)r1 +(2 - 0)r2 | = 12 - r1 + 2r2 | |
| Cj | 0 | 0 | -2 | -1 | 0 |
Notice that the shadow price for the RHS of the equality constraint is the sum of two shadow prices of equivalent constraints, i.e. 1 + 0 = 1, obtainable from the Cj row vector.
The parametric optimal value is 5X1 + 3X2 = 5(14 + r1 - r2) + 3(12 - r1 + 2r2) = 106 + 2r1 + r2. Moreover, the coefficient of r1, and r2 are the shadow prices of the first and the second constraint' RHS value, as expected.
By setting all the parametric RHS to ³ 0, as before, gives the allowable increase and allowable decrease of for each RHS values. Having constructed the general sensitivity region, all other types of sensitivity analysis, such as Parametric, Tolerance analysis can be carried out easily.
Computation of the Generalized B-Inverse Matrix: Notice that, the optimal Parametric RHS contains useful information. For example the coefficients of the parameters constitute what is known as the Basis-Inverse matrix, i.e., the B-1, where the basis B-Matrix is the matrix of the coefficients of the basic variable in the constraint set.
Numerical Example 5: For the numerical example 4, the generalized basis-inverse matrix (not necessarily a square matrix) is:
| r1 | r2 | |
|---|---|---|
| 1 | -1 | |
| 0 | 0 | |
| -1 | 2 |
Since the matrix multiplication of the B-1 time the RHS column vector is the optimal RHS. Therefore, one can verify the fact that the coefficients of the parameters constitute indeed the basis-inverse matrix. The RHS column vector is:
| RHS | |
|---|---|
| 40 | |
| 26 |
The multiplication of the B-1 time the RHS column vector gives:
| Optimal RHS | |
|---|---|
| 14 | |
| 0 | |
| 12 |
This result was expected.
An Alternative New Approach
Based on the Optimal Solution
Knowing the unique optimal solution for the decision variables by using any LP solver, one may construct the simultaneous sensitivity analysis for all RHS values as fallow: Suppose the LP problem has n decision variables and m constraints including the non-negativity conditions (if any).
Step 1: Identify the n constraints that are binding at optimal solution. If there are more than n constraint binding, then the problem is degenerate, which means sensitivity analysis is not applicable.
Step 2: construct the parametric RHS of the constraints, excluding the non-negativity conditions (if any).
Step 3: Solve the parametric system of equations consist of the binding constraints. This provides the parametric optimal solution.
Step 4: To construct the simultaneous sensitivity analysis, plug-in the solution obtain in Step 3, in the all the other parametric constraints, including the non-negativity condition (if any).
The following example illustrates the above procedure.
Numerical Example 6: Consider problem of the numerical example 2, i.e., following LP problem:
Max -X1 + 2X2
subject to:
X1 + X2 ³ 2,
-X1 + X2 ³ 1,
X2 £ 3,
X1 ³ 0,
X2 ³ 0.
There are n = 2 decision variables, and m = 5 constraint.
Step 1: Identify the n=2 constraints that are binding at the given optimal solution (X1 = 0, X2 = 3). The binding constraints are constraints number 3 and 4, namely X2 £ 3, and X1 ³ 0.
Step 2: construct the parametric RHS of the constraints, excluding the non-negativity conditions, i.e,
X1 + X2 ³ 2 + r1,
-X1 + X2 ³ 1 + r2,
X2 £ 3 + r3,
X1 ³ 0,
X2 ³ 0.
Step 3: Solve the parametric system of equations consist of the binding constraints, i.e., solving:
X2 = 3 + r3,
X1 = 0,
This is the parametric optimal solution.
Step 4: The simultaneous sensitivity analysis is obtained by plugging-in this solution in the all the other parametric constraints, including the non-negativity condition (if any). That is, plugging-in X1 = 0, and X2 = 3 + r3 into:
X1 + X2 ³ 2 + r1,
-X1 + X2 ³ 1 + r2,
X2 ³ 0.
By some little algebra, the simultaneous sensitivity analysis for simultaneous changes in any number of RHS values is the following set:
The largest Sensitivity Region for the
RHS of Constraints
The problem is to find a range for each cost coefficient C(j), of variable Xj, such that the current optimal solution (i.e. extreme point) remains optimal.
We need to construct the parametric version of the last row in the optimal tableau by performing the following matrix manipulations:
[current parametric coefficients] - [ parametric coefficients of BV as they appeared in the optimal tableau]. [the body of the optimal tableau]
Numerical Example 7: As our numerical example, we will use the LP problem analyzed in example 2:
Max -X1 + 2X2
subject to:
X1 + X2 ³ 2,
-X1 + X2 ³ 1,
X2 £ 3,
and X1, X2 ³ 0.
Introducing slack/surplus variables for converting the constraints into equality form, we have:
X1 + X2 - S1 = 2,
-X1 + X2 - S2 = 1,
X2 + S3 = 3,
and all variables are non-negative.
The optimal tableau for this problem is:
| BVS | X1 | X2 | S1 | S2 | S3 | RHS | |
|---|---|---|---|---|---|---|---|
| S2 | 1 | 0 | 0 | 1 | 1 | 2 | |
| X2 | 0 | 1 | 0 | 0 | 1 | 3 | |
| S1 | -1 | 0 | 1 | 0 | 1 | 1 | |
| Cj | -1 | 0 | 0 | 0 | -2 |
Consider, for example changing C(1) = -1, to -1 + c1, the parametric version of the last row in the optimal tableau is:
| [-1+c1, 2, 0, 0, 0] | - | [0, 2, 0] | | 1 0 0 1 1 | |
| | 0 1 0 0 1 | | |||
| |-1 0 1 0 1 | |
Multiplying the second matrix by the third one, and after some algebra we have:
[-1+c1, 2, 0, 0, 0] - [0, 2, 0, 0, 2] = [-1+c1, 0, 0, 0, -2]
To check our computations, if we set c1 = 0, we should get the last row of our current optimal tableau.
To maintain optimality, all elements of the parametric version of the last row of the optimal tableau must be £ 0, we have:
-1 + c1 £ 0. This gives c1 £ 1. Therefore the allowable increase is 1, while allowable decrease is as much as you want.
Similarly, sensitivity range for C(2) is as follows: changing C(2) = 2, to 2 + c2, the parametric version of the last row in the optimal tableau is:
| [-1, 2+c2, 0, 0, 0] | - | [0, 2+c2, 0] | | 1 0 0 1 1 | |
| | 0 1 0 0 1 | | |||
| |-1 0 1 0 1 | |
Multiplying the second matrix by the third one, and after some algebra we have:
[-1, 2+c2, 0, 0, 0] - [0, 2+c2, 0, 2+c2] = [-1, 0, 0, 0, -2-c2]
To check our computations, if we set c2 = 0, we should get the last row of our current optimal tableau.
Setting all elements of the parametric version of the last row of the optimal tableau to £ 0, we have:
-2 - c2 £ 0. This gives c2 ³ -2. Therefore the allowable decrease is 2, while allowable increase is as much as you want.
If you are not comfortable with working with large matrices, an alternative to the above procedure is to construct the sensitivity range for the RHS of the dual problem.
Numerical Example 8: As another example, consider the Carpenter's Problem:
Max 5 X1 + 3 X2
Subject to:
2 X1 + X2 £ 40 labor constraint
X1 + 2 X2 £ 50 material constraint
and both X1, X2 are non-negative.
Clearly, changing the profit on each product changes the slope of the iso-value objective function. For small changes the optimal stays at the same extreme point. For larger changes the optimal solution moves to another point. Then we have to modify the formation and solve a new problem.
Following the same procedure as in example 7, but perturbing both cost coefficients by c1, and c2 respectively, one obtains the general sensitivity region for simultaneous, independent (or dependent) changes in both cost coefficients.
Alternatively, one may construct the RHS's sensitivity region for the dual problem. The dual problem for the Carpenter's Problem is:
Minimize 40 U1 + 50 U2
Subject to:
2U1 + 1U2 ³ 5 Net Income from a table
1U1 + 2U2 ³ 3 Net Income from a chair
and U1, U2 are non-negative.
Implementing any of the solution algorithm presented in the Artificial-free Strategic Solution Algorithms site, one obtains the following optimal simplex tableau:
| BVS | U1 | U2 | S1 | S2 | RHS | |
|---|---|---|---|---|---|---|
| U2 | 0 | 1 | 1/3 | -2/3 | 1/3 | |
| U1 | 1 | 0 | -2/3 | 1/3 | 7/3 | |
| Cj | 0 | 0 | -10 | -20 |
The optimal tableau shows that the optimal solution is U1 = $7/3 and U2 = $1/3 with the optimal value of $110 as expected.
The parametric RHS version of this problem is:
Minimize 40 U1 + 50 U2
Subject to:
2U1 + 1U2 ³ 5 + c1
1U1 + 2U2 ³ 3 + c2
and U1, U2 are non-negative.
Following the same procedure but perturbing both cost coefficients' by c1, and c2 respectively, considering the columns of slack/surplus in the optimal tableau, one obtains the following parametric RHS's.
| BVS | U1 | U2 | S1 | S2 | Parametric RHS | |
|---|---|---|---|---|---|---|
| U2 | 0 | 1 | 1/3 | -2/3 | 1/3 -c1/3 +2c2/3 | |
| U1 | 1 | 0 | -2/3 | 1/3 | 7/3 + 2c1/3 - c2/3 | |
| Cj | 0 | 0 | -10 | -20 |
Therefore, by perturbing both cost coefficient in the Carpenter's Problem by c1, and c2 respectively, one obtains the general sensitivity region for simultaneous, independent (or dependent) changes in both cost coefficients as follow:
The following, region depicts the general sensitivity analysis for the cost coefficients' values of the Carpenter's Problem:
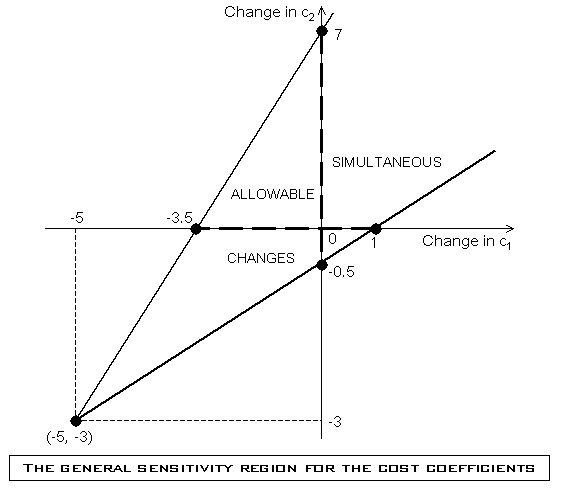
Click on the image to enlarge it and THEN print it.
General Sensitivity Region for Cost Coefficients
Notice that, the sensitivity region contains the origin which, corresponds to the nominal problem. Furthermore the vertex of the sensitivity region is at the point (-5, -3) where both cost coefficients vanish.
Having constructed the general sensitivity region for both the RHS, and the Cost Coefficients, all other types of sensitivity analysis, such as Parametric, Tolerance analysis can be carried out easily.
The largest Sensitivity Region for the
Objective Function Coefficients
Knowing the unique nondegenerate optimal solution for the dual problem by using any LP solver, one may construct the simultaneous sensitivity analysis for all coefficient of the objective function of the primal problem as fallow.
Step 0: Construct and solve the dual problem. Suppose the dual problem has n decision variables and m constraints including the non-negativity conditions (if any).
Step 1: Identify the n constraints that are binding at optimal solution. If there are more than n constraint binding, then the primal problem may have multiple solutions, which means sensitivity analysis is not applicable.
Step 2: construct the parametric RHS of the constraints, excluding the non-negativity conditions (if any).
Step 3: Solve the parametric system of equations consist of the binding constraints. This provides the parametric optimal solution.
Step 4: To construct the simultaneous sensitivity analysis, plug-in the solution obtain in Step 3, in the all the other parametric constraints, including the non-negativity condition (if any).
The following example illustrates the above procedure.
Numerical Example 9: Consider problem of the numerical example 2, i.e., following LP problem:
Max -X1 + 2X2
subject to:
X1 + X2 ³ 2,
-X1 + X2 ³ 1,
X2 £ 3,
X1 ³ 0,
X2 ³ 0.
Step 0: Construct the dual problem:
Min -U1 - U2 + 3U3
subject to:
-U1 + U2 ³ -1,
-U1 - U2 + U3 ³ 2,
U1 ³ 0,
U2 ³ 0,
U3 ³ 0.
The optimal solution is U1 = 0, U2 = 0, U3 = 2. The dual problem has n = 3 decision variables and m = 5 constraints including the non-negativity conditions (if any).
Step 1: Identify the n = 3 constraints that are binding at optimal solution:
-U1 - U2 + U3 ³ 2,
U1 ³ 0,
U2 ³ 0,
Step 2: construct the parametric RHS of the constraints, excluding the non-negativity conditions (if any):
-U1 + U2 ³ -1 + c1,
-U1 - U2 + U3 ³ 2 + c2,
U1 ³ 0,
U2 ³ 0,
U3 ³ 0.
Step 3: Solve the parametric system of equations consist of the binding constraints,
-U1 - U2 + U3 ³ 2 + c2,
U1 ³ 0,
U2 ³ 0.
This provides the parametric optimal solution:
U1 = 0,
U2 = 0,
U3 = 2 + c2
Step 4: The simultaneous sensitivity analysis for the coefficients of the objective function for the primal problem is obtained by plugging-in this solution in the all the other parametric constraints, including the non-negativity condition (if any). That is, plugging-in U1 = 0, U2 = 0, and U3 = 2 + c2 into:
-U1 + U2 ³ -1 + c1,
U3 ³ 0.
By some little algebra, the simultaneous sensitivity analysis for simultaneous changes in coefficients of the objective function for the primal problem is the following set:
Numerical Example 10: As another numerical example consider the following production problem:
Maximize f(X) = 4X1 + 2X2 + 3X3
Subject to:
X1 + X2 + X3 £ 10
3X1 + X3 £ 24
X1 ³ 0
X2 ³ 0
X3 ³ 0
The optimal solution is (X1 = 7, X2 = 0, X3 = 3) which is unique and non-degenerate with a maximum value of 37.
Since this numerical example is a three dimensional LP, one expects (at least) to have three binding constraints. The binding constraints are:
X1 + X2 + X3 = 10
3X1 + X3 = 24
X2 = 0
Computation of shadow prices: By definition, the shadow price for a non-binding constraint is always zero. To compute the shadow price of binding constraints, one must first construct and solve the RHS parametric of the above system of equations, excluding any non-negativity condition (in this example, X2 = 0). By plugging X2 = 0, the above system of equations reduces to:
X1 + X3 = 10 + R1
3X1 + X3 = 24 + R2
Solving the system of equations, we get the following parametric solution:
X1 = 7 - 0.5R1 + 0.5R2
X2 = 0
X3 = 3 + 1.5R1 - 0.5R2
The solution can be verified by substitution. For larger problem one may use the JavaScript available using the following link:
http://home.ubalt.edu/ntsbarsh/Business-stat/otherapplets/PaRHSSyEqu.htm
Plugging the parametric solution into objective function, we have:
f(X) = 4X1 + 2X2 + 3X3 = 37 + 2.5R1 + 0.5R2
Notice that the parametric objective function f(X) = 37 + 2.5R1 + 0.5R2 is valid when the parametric solution satisfies all non-binding (i.e., the unused) constraints at the parametric optimal solution. In our current numerical example, unused constraints are the following non-negativity conditions; therefore they do not have parametric RHS:
One can find the ordinary one-change-at-a-time sensitivity range for each one of the two RHS of the constraints. The range for the RHS of the first constraint (RHS1) can be obtained by setting R2 = 0 in the above two inequalities. This implies that R1 £ 14 and R1 ³ -2. Therefore, the allowable increase and decrease in the current value 10 for RHS1 are 14 and 2, respectively. Similarly, the range for the RHS of the second constraint (RHS2) can be obtained by setting R1 = 0 in the above two inequalities. This implies that R2 ³ -14 and R2 £ 6. Therefore the allowable increase and decrease in the current value 24 for RHS2 are 6 and 14, respectively.
Obtaining the Optimal Solution to the Dual Problem: The shadow price is a derivative of the parametric optimal function, i.e., U1 = 2.5, U2 = 0.5, for two resources with RHS equal to 10 and 24, respectively. These shadow prices are the solution to the following corresponding dual problem:
Minimize 10U1 + 24U2
subject to:
U1 + 3U2 ³ 4
U1 ³ 2
U1 + U2 ³ 3
U1 ³ 0
U2 ³ 0
The dual optimal value of 37 is equal to the optimal value of the primal problem, as expected.
Construction of the Largest Sensitivity Regions for the Coefficients of the Objective Function: To find the region ranges for objective coefficients function, one may use the RHS parametric version of the dual problem; that is:
Minimize 10U1 + 24U2
Subject to:
U1 + 3U2 ³ 4 + C1
U1 ³ 2 + C2
U1 + U2 ³ 3 + C3
U1 ³ 0
U2 ³ 0
As calculated earlier, the shadow prices are U1 = 2.5, U2 = 0.5, which are the optimal solution to the dual. The first and the third constraints are binding. The parametric presentations of the RHS of these binding constraints are as follows:
U1 + 3U2 = 4 + C1,
U1 + U2 = 3 + C3
Solving these equations we get the following parametric solution:
U2 = 0.5 + 0.5C1 - 0.5C3
Finding the Cost Sensitivity Range by Grapical Method: It is a commonly held belief that one can compute the cost sensitivity range by bracketing the (perturbed) slope of the (iso-value) objective function by the slopes of the two lines resulting from the binding constraints. This graphical slope-based method to compute the sensitivity ranges is described in popular textbooks, such as Anderson et al., (2007), Lawrence and Pasternack (2002), and Taylor (2006).
Unfortunately these are misleading. Warning should have been given that their approach is not general and works if and only if the coefficients do not change sign.
In an LP with 2 variables and inequality constraints, suppose we have a unique, non-degenerate optimum at the intersection of two lines, as shown in the following figure. Then, the range of objective coefficients for which this solution remains optimal is given by the slopes of the two lines.
The following is a counterexample. It points out that one must be careful to state that the coefficients do not change sign.
Counterexample: Maximixe 5X1 + 3X2
X1 + X2 £ 2,
X1 - X2 £ 0,
X1 ³ 0, X2 ³ 0.
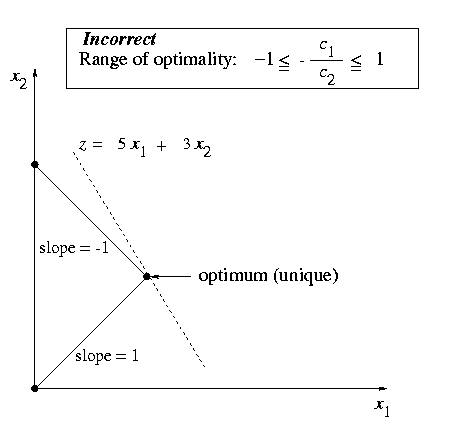
Dealing with LP problem with Degenerate
and/or Multiple Optimal Solutions
There is a need to extend and construct the largest and general sensitivity analysis regions (SAR) for LP models. Unlike the ordinary sensitivity analysis, the SAR allows us to analyze any type of changes, including dependent, independent, and multiple changes in both the right-hand-side values of the constraints and the coefficients of the objective function simultaneously. The study should include SAR construction for problems with primal and/or dual degenerate optimal solutions; the following LP problem is a good case to work with:
Maximize f(X) = X1 + X2 + 4X3
Subject To:
X1 + 2 X3 £ 2,
X2 + 2 X3 £ 2,
X1 £ 2,
X2 £ 2,
X3 £ 2,
X1 ³ 0,
X2 ³ 0,
X3 ³ 0.
The feasible region is illustrated in the following figure:
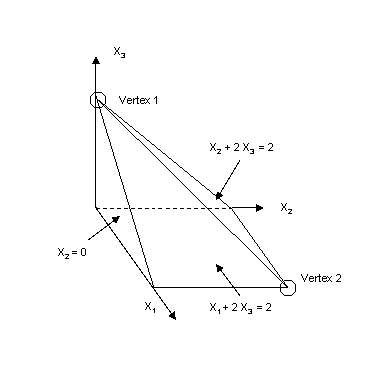
Click on the image to enlarge it and THEN print it.
This problem has two optimal vertices: Vertex 1 with coordinates (0, 0, 1) and Vertex 2 with coordinates (2, 2, 0). Being a three dimensional problem, however, at both vertices more than three constraints are binding, therefore both are degenerate solutions. Moreover, both are genuine degeneracy caused not by redundant constraints, since deleting only one of the above constraints changes the set of feasible solutions.
Therefore, besides having degenerate solution, this nice problem has also multiple solutions. The set of all optimal solution is the edge line segment vertex1-vertex2, shown on the above figure which can be expressed as the convex combination of the two optimal vertices, i.e.:
(X1 = 2l2, X2 = 2l2, X3 = l1), with the parametric optimal value is f(X) = X1 + X2 + 4X3 = 4l1 + 4l2 , where l1 + l2 = 1, l1 ³ 0, l2 ³ 0.
Multiple solutions means having more than one optimal solution, in such as a case the decision maker may wish to do further selection or just leave it to what the solver reports. For example, the interior point methods often report a linear combination of the optimal basic solutions. Degeneracy and multiple optima are different concepts. Having multiple optimal solutions does mean that the dual problem has a degenerate solution however, one may have multiple non-degenerates optimal, or a unique solution that is degenerate, or even a combination, as is the case for the above interesting problem.
Maintaining a Degenerate Optimal Solution
Consider the following two-dimensional problem:
Maximize f(X) = X1 + X2
Subject to:
X1 £ 1
X2 £ 1
X1 + X2 £ 2
X1 ³ 0, X2 ³ 0.
The optimal solution is X1 = 1, and X2 = 1, at which all three constraints are binding. We are interested in finding out how far the RHS of binding constraints can change while maintaining the degeneracy of the degenerate optimal solution. Because of degeneracy, there is dependency among these constraints at binding position, that is:
X1 = 1
X2 = 1
X1 + X2 = 2
In order to maintain the degenerate vertex while changing the RHS values, one must change the RHS proportion to the coefficient of the decision variables. That is, having parametric RHS system of equations:
X1 = 1 + 1r1 + 0r2
X2 = 1 + 0r1 + 1r2
X1 + X2 = 2 + 1r1 + 1r2
Having two decision variables, one may take any two of the parametric equations to find the parametric degenerate optimal solution. For example, the first two equations provide (X1 = 1 + r1, X2 = 1 + r2) which clearly satisfies the third one.
For larger problems one may use the JavaScript:
http://home.ubalt.edu/ntsbarsh/Business-stat/otherapplets/PaRHSSyEqu.htm
The perturbed optimal value is f(X) = X1 + X2 = 2 + r1 + r2. In order that this vertex remains optimal, it must be satisfied the other constraints, which is those constraints which are not used in any computation up to now. For this numerical example, the non-negativity conditions are the remaining constraints; therefore, one obtains the following conditions for r1 and r2:
Maintaining the Multiplicity of Multiple Optimal Solutions
Consider the following problem which has many solutions:
Maximize 6X1 + 4X2
Subject to:
X1 + 2X2 £ 16
3X1 + 2X2 £ 24
all decision variables ³ 0.
It has two vertices as optimal, namely, (X1 = 8, X2 = 0) and (X1 = 4, X2 = 6). Notice that, the existence of multiple solutions means we have innumerable optimal solutions. For example, for the above problem, all the following solutions are indeed optimal:
Minimize 16U1 + 24U2
subject to:
U1 + 3U2 ³ 6
2U1 + 2U2 ³ 4
all decision variables ³ 0.
The Dual is has a degenerate optimal solution (U1 = 0, U1 = 2). In order to maintain the degenerate vertex while changing the RHS values, one must change the RHS proportion to the coefficient of the decision variables. That is, having parametric RHS system of equations:
U1 + 3U2 = 6 + 1c1 + c2
2U1 + 2U2 = 4 + 2c1 + 2c2
U1 = 0 + 1c1
Having two decision variables, one may take any two of the parametric equation to find the parametric degenerate optimal solution. For example, the first two equations provide
In order that this vertex remains optimal, it must be satisfied the other constraints, which is those constraints which are not used in any computation up to now. For this numerical example, the non-negativity condition is the remaining constraint U2 ³ 0. Therefore, one obtains the following conditions for c1, and c2:
Notice that, since in higher dimensions, the multiple solutions could occur for example, on an edge of feasible region, therefore a deeper analysis is needed for the last part.
Updating the Current Solution for Small Changes in the Technology Matrix A
Change in One element in the Technology Matrix A: Let B denotes the current basis matrix with its inverse denoted by B-1. Further let dij and dij-1 denotes the element in the ith row and jth column of B and B-1, respectively. If an element in row i and column j in matrix B is changed by d, then the new B-1 can be obtained by updating the old one as follow:
Where Ei is a row vector of zeros with one in the ith location and EjT denotes the transpose of vector Ej.
The updated solution is: X = Bnew-1.b
The algorithm for updating the current solution when both rows and columns elements are perturbed is given in Arsham (2006).
The More-for-less & Less-for-more Situations
Consider the following production problem:
Max X1 + 3X2 + 2X3
subject to:
X1 + 2X2 + X3 = 4
X1 + 5X2 = 9
X1 ³ 0
X2 ³ 0
X3 ³ 0
Using the The solution can be verified by substitution. For larger problem one may use the JavaScript: Algebraic Method, because all constraints are in equality form, it has two vertices, namely (1, 0, 3) and (2.8, 0.6, 0). As before, using the parameters l1 and l2 for the two feasible vertices where l1 ³ 0, l2 ³ 0 and l1 + l2 = 1, we obtain the following parametric representation of the feasible region:
X1 = l1 + 2.8l2
X2 = 0.6l2
X3 = 3l1
The parametric objective function is:
f(l) = X1 + 3X2 + 2X3 = 7l1 + 4.6l2.
Clearly, the optimal solution occurs when l1= 1, and l2 = 0, with maximum value of 7. Therefore, the optimal solution is X1 = 1, X2 = 0, X3 = 3, one of the vertices.
Now, if you change the second available labor from 9 to 12, the optimal value would be $4. That is, you have worked more hours for less profit. This situation arises frequently and is known as "The More-for-less Paradox". The resource number 2 has a negative shadow price.
To see that, we solve the RHS perturbed equation constraints, with X2 = 0,
X1 + X3 = 4 + r1
3X1 + 2X3 = 9 + r2
The Parametric solution is X1 = 1 – 2r1 + r2, X2 = 0, and X3 = 3 + 3r1 - r2 , the optimal parametric solution is:
f(X) = X1 + 3X2 + 2X3 = 7 + 4r1 - r2 , with constraints:
X1 = 1 – 2r1 + r2 ³ 0, X3 = 3 + 3r1 - r2 ³ 0.
Notice that the shadow price of the second constraint is negative. To find out the best number of hours, one must work to maximize the profit function 7 + 4r1 - r2 , by setting r1 = 0 and finding the largest negative value for r2. Therefore, the constraints reduce to:
X1 = 1 + r2 ³ 0, X3 = 3 - r2 ³ 0. The largest negative value for r2 is r2 = -1. This give the optimal solution of (X1 = 0, X2 = 0, X3 = 4) with optimal value of f(X) = X1 + 3X2 + 2X3 = 8.
Therefore, the optimal strategy is to work 8 hours instead of 9.
Proposition: The necessary and sufficient condition for the existence of the more-for-less for maximization problem (less-for-more for minimization problem) situation is to have equality constraint(s) with negative (positive) shadow price(s).
Also visit also the following Web site:
Sensitivity Analysis
References and Further Readings:
Adler I., and R. Monteiro, A geometric view of parametric linear programming, Algorithmica, 8, 161-176, 1992.
Anderson D., Sweeney D., and Williams T., An Introduction to Management Science, West Publisher, 2007.
Arsham H., Construction of the largest sensitivity region for general linear programs, Applied Mathematics and Computation, 189(2), 1435-1447, 2007.
Arsham H., Perturbed matrix inversion with application to LP Simplex method, Applied Mathematics and Computation, 188(1), 801-807, 2007.
Arsham H., Perturbation analysis of general LP models: A unified approach to sensitivity, parametric tolerance, and more-for-less analysis, Mathematical and Computer Modelling, 12, 1437-1446, 1990.
Aucamp D., and D. Steinberg, The computation of shadow price in linear programming, Journal of Operational Research Society, 33, 557-565, 1982.
Berkelaar A. , C. Roos, and T. Terlaky, The optimal set and optimal partition approach to linear and quadratic programming. Chapter 6 in Advances in Sensitivity Analysis and Parametric Programming, T. Gal and H. J. Greenberg, eds., Kluwer Academic Publishers, 1997.
Borges A., and C. Antunes, A visual interactive tolerance approach to sensitivity analysis in MOLP, European Journal of Operational Research, 142, 357-381, 2002.
Evans J., and N. Baker, Degeneracy and the (mis)interpretation of sensitivity analysis in linear programming, Decision Sciences, 13, 348-354, 1982.
Gass S., and S. Vinjamuri, Cycling in linear programming problems, Computers & Operations Research, 31, 303-311, 2004.
Greenberg H., Simultaneous primal-dual right-hand-side sensitivity analysis from a strictly complementary solution of a linear program, SIAM Journal of Optimization, 10, 427-442, 2000.
Jansen B., Sensitivity analysis in linear programming: just be careful!, European Journal of Operational Research, 101, 15-28, 1997.
Lawrence J., Jr., and B. Pasternack, Applied Management Science: Modeling, Spreadsheet Analysis, and Communication for Decision Making, John Wiley and Sons, 2002.
Taylor III, B., Introduction to Management Science, Prentice Hall, 2006.
Yildirim E., A unifying optimal partition approach to sensitivity analysis in conic optimization, Journal of Optimization Theory and Applications, 122, 405-423, 2004.
The Copyright Statement: The fair use, according to the 1996 Fair Use Guidelines for Educational
Multimedia, of materials presented on this Web site is permitted for non-commercial and classroom purposes only.
This site may be mirrored intact (including these notices), on any server with public access, and linked to other Web pages. All files are available at
http://home.ubalt.edu/ntsbarsh/Business-stat for mirroring.
Kindly e-mail me your comments, suggestions, and concerns. Thank you.
This site was launched on 2/25/1994, and its intellectual materials have been thoroughly revised on a yearly basis. The current version is the 8th Edition. All external links are checked once a month.