Construcción de Regiones de Sensibilidad General
de Programación Lineal

Sitio Espejo para América Latin

Esta es la versión en Español del sitio Web principal en Inglés, el cual se encuentra disponible en:
Construction of General Sensitivity Regions

USA Site

Este sitio presenta una metodología para la construcción de regiones de sensibilidad de programación lineal (PL). A diferencia del análisis ordinario de sensibilidad, esta construcción nos permite analizar cualquier tipo de cambios, incluyendo dependientes, independientes y cambios múltiples tanto en los valores de derecha (RHS) como en los coeficientes de coste de PL.

Professor Hossein Arsham   

Para buscar en este sitio, trate Edit | Find in page [Ctrl + f]. Escriba la palabra o frase, ej. "parámetro " o "lineal " Si la primera palabra o frase encontrada no es lo que busca, trate Find Next.

---

   MENU

1. Introducción
2. ¿Por qué Análisis de Sensibilidad?
3. Manejando la Incertidumbre
4. Una Clasificación de Análisis de Sensibilidad
5. Herramientas para la Construcción de la Región de Sensibilidad
6. Sensibilidad de los Valores de Derecha (RHS) de las Restricciones:
   Los precios sombra permanecen sin alterar
7. Análisis de los Modelos de PL con Restricciones de Igualdad
8. Cálculo de la Matriz B-inversa Generalizada
9. Un Enfoque Nuevo Alternativo
10. Sensibilidad de los Coeficientes de la Función Objetiva
    La estrategia óptima para las variables de decisiones cuando estas permanecen sin ser alteradas
11. Un Enfoque Nuevo Alternativo
12. La actualización de la Estrategia Óptima para Cambios en la Matriz de Tecnología

---

Introducción

A diferencia del análisis de sensibilidad ordinario ordinary sensitivity analysis, la construcción presentada aquí nos permite hacer cambios dependientes, independientes o múltiples tanto en los valores de derecha como en los coeficientes de coste de modelos de programación lineal de solución única.

La incertidumbre en un modelo puede tener varios orígenes en diferentes problemas de decisión. Puede ser debido a información incompleta, fluctuaciones inherentes al problema, o cambios imprevisibles del futuro.

Uno puede abordar incertidumbres en una manera más “determinista". Este enfoque es llamado en varias formas, así como "el modelo de escenario", "el modelo determinista", "análisis de sensibilidad" y “análisis de estabilidad". La idea es de construir subjetivamente una lista ordenada de incertidumbres con los niveles más altos que podrían tener un mayor impacto en el resultado de correlación eventual. Este es hecho antes de enfocarse en los detalles de cualquier "escenario" en particular o modelo.

Un entendimiento de la influencia de lo antes mencionado en el curso de acción sugerida por el modelo es crucial, porque:
Los diferentes niveles de aceptación (del público general, de los tomadores de decisiones, de los interesados directos) pueden estar vinculados a diferentes tipos de incertidumbre.
Diferentes incertidumbres tienen impacto diferente en la fiabilidad, fortaleza, y eficacia de la construcción.

La importancia de esta construcción (su adaptación a la tarea) depende en gran magnitud del impacto de la incertidumbre en el resultado del análisis. La sorpresa no es un elemento en una decisión óptima robusta.

Los ejemplos de escenarios donde lo anterior se aplica son muchos e incluyen:

• Construcción de por ejemplo, indicadores económicos y ambientales
• Análisis y pronostico de riesgo con aplicaciones de riesgo ambiental, financiero, y de seguros
• Optimización y calibración del modelo

---

¿Por qué el Análisis de Sensibilidad?

A continuación aparece una lista condensada de motivos por los cuales el análisis de sensibilidad debería ser considerado:

Para la toma de dediciones y el desarrollo de recomendaciones para tomadores de decisiones

Para las pruebas de la robustez de una solución óptima. La sorpresa no es un elemento de una decisión óptima robusta.
Para la identificación de valores críticos, umbrales, o valores de equilibrio para los cuales la estrategia óptima cambia.
La identificación de sensibilidad, es decir, parámetros importantes, por ejemplo, en aplicaciones de Elasticidad.
Investigación de soluciones sub-óptimas.
El desarrollo de recomendaciones flexibles que dependen de las circunstancias.
La comparación de los valores de decisiones estratégicas simples y complejas.
La evaluación "del riesgo" de una estrategia o escenario.

Comunicación

Haciendo recomendaciones más creíbles, comprensibles, convincentes, o persuasivas.
Permitiendo a tomadores de decisiones seleccionar suposiciones.
Comunicando una carencia de compromiso de cualquier estrategia individual.
El tomador de dediciones podría incorporar algunas otras perspectivas del problema así como una perspectiva cultural, política, psicológica, etc., en las recomendaciones científicas de la gerencia.

Aumento del Entendimiento o calificación del sistema

La estimación de la relación entre los parámetros y el resultado.
El entendimiento de la relación entre las variables de entrada y de salida.
El desarrollo de pruebas de hipótesis.

Desarrollo del modelo

Las pruebas del modelo de validez o exactitud.
La búsqueda de errores en el modelo.
Simplificación del modelo.
Calibración del modelo.
Como enfrentarse con datos pobres o ausentes.
Priorizando la adquisición de información.

Lista condensada de casos donde el análisis de sensibilidad debería ser considerado:

1. En el control de problemas, el AS (Análisis de Sensibilidad) puede ayudar a identificar regiones críticas en el espacio de los parámetros de entrada.
2. En la proyección de ejercicios, el AS puede ayudar a localizar parámetros influyentes en sistemas con cientos de entradas inciertas.
3. Las técnicas de AS basadas en la varianza son útiles para averiguar si un subconjunto de los parámetros de entrada puede contener (la mayor parte de) la varianza de los valores de salida.
4. El punto anterior (3) puede ser usado para el mecanismo de reducción (eliminando o estableciendo partes no relevantes del modelo) y para el modelo de agrupación (construyendo/extrayendo un modelo de uno más complejo). Ver también el problema de “la importancia" del modelo: ¿son los parámetros en el conjunto de entrada del modelo relevante en la tarea del modelo?
5. El punto (3) puede también ser usado para la identificación del modelo señalando las condiciones experimentales para las cuales su capacidad de discriminar entre el modelo está en el máximo.
6. Como en el punto anterior (5), el AS puede ser usado para la calibración del modelo, para investigar si los experimentos con sus incertidumbres relacionadas permitirán la estimación del parámetro. Este es mayormente útil en problemas mal formulados.
7. El AS puede ser combinado con la optimización / algoritmos de búsqueda; identificando los parámetros más importantes, el AS puede permitir reducir la dimensionalidad del espacio donde la búsqueda es hecha.
8. Como un instrumento de garantía de calidad, el AS asegura que la dependencia de la salida de los parámetros de entrada en el modelo tenga una semejanza física y una explicación.
9. Para solucionar un problema inverso, el AS sirve como un instrumento para extraer parámetros implantados en modelos cuya salida no guarda correlación fácilmente con la entrada desconocida, por ejemplo, en la cinética química, para extraer las constantes cinéticas de los sistemas complejos de la tasa de rendimiento de componentes medida.
10. Para asignar recursos óptimamente en I&D, el AS muestra donde es que vale la pena más invertir a fin de reducir el rango de incertidumbre del modelo.
11. El AS puede establecer en una base cuantitativa qué fracción de mi predicción de incertidumbre es debido a las restricciones de estimación de incertidumbre y que fracción es debida a la incertidumbre estructural.

---

Trabajando con la Incertidumbre

Los enfoques actuales para tratar con incertidumbres incluyen:

Análisis del escenario: En este enfoque uno asume escenarios (por ejemplo ciertas combinaciones de los posibles valores de incertidumbre del parámetro) y soluciona el problema para cada uno. Solucionando el problema repetidamente para diferentes escenarios y estudiando las soluciones obtenidas, el gerente observa sensibilidades y se decide heurísticamente en un aproximado, que es subjetivo.

Análisis del escenario menos favorable: Esta técnica intenta explicar el uso de márgenes de seguridad en el problema en la etapa de planificación.

Enfoque Monte-Carlo: Los modelos estocásticos asumen que la incertidumbre es conocida por su distribución estadística.

---

Una Clasificación del Análisis de Sensibilidad

A diferencia del análisis de sensibilidad ordinario, la construcción presentada aquí nos permite hacer cambios dependientes, independientes o múltiples tanto en los valores de derecha como en los coeficientes de coste como es mostrado en la Figura siguiente. Los cálculos envuelven algunas manipulaciones elementales de la matriz.

Una Clasificación del Análisis de Sensibilidad para Modelos de PL

Teniendo el resultado de una formulación de programa lineal y el cálculo para la solución, una serie de análisis puede proporcionar información gerencial valiosa para tratar con incertidumbres. Estos rangos de incertidumbre pueden ser obtenidos realizando los tipos diferentes siguientes de análisis de sensibilidad según la naturaleza de la incertidumbre: análisis de perturbación; análisis de tolerancia; análisis simétrico de tolerancia individual; análisis simétrico de tolerancia; análisis paramétrico de sensibilidad; y análisis de sensibilidad ordinario.

Análisis de Perturbación: los cambios simultáneos e independientes de cualquier parámetro en cualquier dirección (sobre o bajo estimación) para cada parámetro que mantienen la base óptima. Esto proporciona un conjunto más grande de perturbaciones.

Análisis de Tolerancia: los cambios simultáneos e independientes expresados como el porcentaje aceptable máximo de valor del parámetro en cualquier dirección (sobre o bajo estimación) para cada parámetro que mantiene la base óptima. Esto proporciona un rango de valores para cada parámetro.

Análisis Simétrico de Tolerancia Individual: los cambios iguales simultáneos e independientes expresados como el porcentaje aceptable máximo del valor de los parámetros en ambas direcciones (sobre o bajo estimación) para cada parámetro que mantiene la base óptima. Esto proporciona un rango de valores para cada parámetro con el valor actual en su centro.

Análisis Simétrico de Tolerancia: los cambios simultáneos e independientes iguales expresados como el porcentaje máximo aceptable del valor del parámetro en ambas direcciones (sobre y bajo la estimación) para toda actividad que mantenga la base óptima. Este proporciona un rango único de valores de incertidumbre para todos los parámetros.

Análisis Paramétrico: cambios simultáneos de los valores del parámetro dependiente en sus valores nominales que mantienen la base óptima. Esto proporciona la magnitud máxima del cambio para valores de parámetros dependientes.

Análisis de Sensibilidad Ordinario: Un cambio a la vez de cualquier valor del parámetro que mantiene la base óptima. Esto proporciona un rango para el cambio de cualquier valor de parámetro específico, manteniendo a todos los otros en sus valores nominales.

En la realización de los diferentes tipos de análisis de sensibilidad mencionados anteriormente, las computaciones necesarias son algunas operaciones de la matriz elementales de las herramientas disponibles para construcción de regiones de sensibilidad.

---

Instrumentos para Construcción de la Región de Sensibilidad

Respecto a el Problema del Carpintero (the Carpenter's Problem), para pequeños cambios de cualquiera de los recursos la estrategia óptima (es decir; haga la mezcla del producto) permanece válida. Para cambios más grandes estos movimientos de estrategia óptima cambian y el Carpintero debe hacer todas las mesas o todas las sillas que él/ella pueda hacer. Este es un cambio drástico de la estrategia, por lo tanto, nosotros tenemos que revisar la formulación y solucionar un nuevo problema.

Aparte de la información necesaria mencionada anteriormente, también estamos interesados en saber cuánto el Carpintero puede vender (o comprar) cada recurso a un precio Razonable (o costo). ¿Es decir a qué punto podemos nosotros aumentar o disminuir los valores de RHS(i) para un (i) fijo manteniendo la validez del precio sombra actual del valor de RHS(i)? Es decir a que distancia podemos nosotros aumentar o disminuir el valor RHS(i), para un (i) fijo manteniendo la solución óptima actual con (El Problema Dual) The Dual Problem?

Históricamente, el precio sombra fue definido como la mejora del valor de la función objetivo por cada unidad de aumento en el valor de mano derecha, porque el problema a menudo era puesto en forma de la maximización de la ganancia, mejora significa incremento.

Sepa también que, para cualquier valor de RHS, el precio sombra (conocido también, como su valor marginal), es la cantidad de cambio del valor óptimo proporcional a un cambio unitario en un valor RHS en particular. Sin embargo, en algunos casos no es permitido cambiar el valor de RHS en gran dimensión. El rango de sensibilidad para el valor de RHS proporciona los valores para los cuales el precio sombra tiene un significado tan económico, y permanece sin alterar.

Como parte de la solución post-óptima, estamos interesados en encontrar el rango de sensibilidad para los valores de RHS, y los coeficientes de la función objetivo.

Todas las herramientas que necesitamos para realizar el análisis de sensibilidad están al instante disponibles en la tabla final del simplex. La primera columna de esta tabla contiene el vector variable básico cuyo valor óptimo está contenido en la última columna llamada el vector de columna RHS. El contenido de la tabla contiene una matriz de identidad correspondiente a las variables básicas y la matriz de variables no básica denotada por BNB. La última fila de esta tabla es llamada la fila de C_j.

Ejemplo Numérico 1: Considere el problema de PL siguiente, nos referiremos a este como (el Problema del Carpintero) the Carpenter's Problem:

Max 5 X1 + 3 X2

Sujeto a:
2 X1 + X2 £ 40 restricción de labor
X1 + 2 X2 £ 50 restricción de materiales
y ambos X1, X2 son no negativos.

Introduciendo variables de holgura para convertir las restricciones en la forma de igualdad, tenemos:

Max 5 X1 + 3 X2

Sujeto a:
2 X1 + X2 + S1 = 40
X1 + 2 X2 + S2 = 50
todas las variables son no negativas.

Las herramientas del Análisis de Sensibilidad: las siguientes herramientas del análisis de sensibilidad son también asequibles utilizando (las herramientas de Optimización Lineal con análisis de sensibilidad de JavaScript)Linear Optimization with Sensitivity Analysis Tools JavaScript.

La Estrategia Óptima para las Variables de Decisión son: X1 = 10, X2 = 20. Uno puede encontrar el valor de la variable de holgura/excedente Si para la restricción i, substituyendo la estrategia óptima en la restricción i ^ésima. Ya que las variables no básicas son siempre iguales a cero, para este problema, ambas variables de holgura S1 y S2 son cero.

La Matriz de Variables No básica B_NB es:

S1	S2
2/3	-1/3
-1/3	2/3

El Vector de Fila de C_j es:

X1	X2	S1	S2
0	0	-7/3	-1/3

Los elementos de Cj corresponden a las Variables de Decisión en la misma secuencia que ellos aparecieron en la función objetivo, luego seguido de las Variables de holgura/excedente. El elemento Cj para las Variables Básicas es siempre igual a cero.

Note que el número de elementos cero en el vector de fila de Cj debe ser igual al número de restricciones, de no ser así el problema podría tener soluciones múltiples, y por lo tanto cualquier resultado del análisis de sensibilidad podría ser irreal.

Note que el precio sombra del valor de RHS i ^ésimo es igual a menos uno multiplicado por el elemento del vector C_j en la columna de Si. Para este ejemplo numérico los precios sombra U1 y U2 de los primeros y segundos valores de RHS (50 y 50), son U1 = (-1) (-7/3) = $7/3 y U2 = (-1) (-1/3) = $1/3. Claramente, esta es también la estrategia de solución óptima para (El Problema Dual) The Dual Problem.

El Vector de Columna RHS es:

RHS
10
20

Los elementos de RHS son el valor de Variables Básicas. Además, ellos son siempre no negativos. El valor óptimo de todas las variables no básicas es siempre igual al cero.

Note que si algún elemento en la columna de vector RHS es cero, entonces la solución óptima podría ser (la solución degenerada) degenerate solution, por lo tanto cualquier resultado de análisis del sensibilidad podría ser irreal.

Construcción de la tabla óptima Simplex: la primera fila de la tabla óptima Simplex contiene los nombres de la variable de decisión en el mismo orden en que ellos aparecieron en la función objetivo, seguido por la variable de holgura/excedente correspondiente al orden de las restricciones. El resto de elementos de la tabla óptima se puede llenar con las herramientas de (Optimización Lineal con Análisis de Sensibilidad JavaScript) Linear Optimization with Sensitivity Analysis Tools JavaScript.

La tabla óptima Simplex para este problema es:

BVS	X1	X2	S1	S2	RHS
X1	1	0	2/3	-1/3	10
X2	0	1	-1/3	2/3	20
Cj	0	0	-7/3	-1/3

---

Sensibilidad de los Valores de Derecha de las Restricciones:
Los precios sombra permanecen sin alterar.

En esta sección, estamos interesados en investigar bajo que condiciones los valores marginales actuales de los valores de RHS de las restricciones permanecen sin alterar

Ejemplo Numérico 2: Considere el problema de PL siguiente:

Max -X1 + 2X2
sujeto a:
X1 + X2 ³ 2,
-X1 + X2 ³ 1,
X2 £ 3,
y X1, X2 ³ 0.

Introduciendo variables de holgura/excedente para convertir las restricciones en forma de igualdad, tenemos:

X1 + X2 - S1 = 2,
-X1 + X2 - S2 = 1,
X2 + S3 = 3,
y todas las variables son no negativas.

La tabla óptima para este problema es:

BVS	X1	X2	S1	S2	S3	RHS
S2	1	0	0	1	1	2
X2	0	1	0	0	1	3
S1	-1	0	1	0	1	1
Cj	-1	0	0	0	-2

Considere cambiar el RHS (1) de 2 a 2 + r1. El RHS paramétrico para la tabla óptima es el RHS actual en la tabla óptima más (si la restricción es £), y menos (si la restricción es ³) la columna de S (i) multiplicada por r1.

2 - (0). r1
3 - (0). r1
1 - (1). r1 Para mantener la viabilidad, todos los elementos del RHS paramétrico deben ser no negativos. Esto da como resultado:

1 - r1 ³ 0, que es r1 £ 1. Por lo tanto, la cantidad del aumento aceptable es 1, y la disminución aceptable es tanto como usted quiera.

Del mismo modo, para RHS (2)= 1, cambiándolo a 1 + r2, el RHS paramétrico en la tabla óptima es:

2 - (1). r2
3 - (0). r2
1 - (0). r2

Esto da 2-r2 ³ 0, que es r2 £ 2. Por lo tanto, la cantidad de aumento aceptable es 2, y la disminución aceptable es tanto como usted quiera.

Para el RHS (3) =3, cambiándolo a 3 + r3, el RHS paramétrico es:

2 + (1). r3
3 + (1). r3
1 + (1). r3

Poniendo todos los elementos a ³ 0, da como resultado r3 ³ -1. Por lo tanto la disminución aceptable es 1, mientras el aumento aceptable es tanto como usted quiera.

Note que, el valor óptimo paramétrico con r3 como su parámetro es:-X1 + 2X2 = 0 + 2 (3 + r3) = 6 + 2r3. Substituyendo r3 = 0, esto da el valor óptimo. Note también que, el coeficiente de r3 en el valor óptimo paramétrico es 2 que es el precio sombra del RHS de la 3^ra restricción, esta observación es siempre verdadera. Por eso, declaramos anteriormente que, el precio sombra (valor marginal), es la cantidad de cambio en el valor óptimo en proporción a un cambio unitario para este RHS en particular.

Aunque restrinjamos nuestra discusión a un cambio de RHS a la vez, en el ejemplo anterior, uno puede ampliarlo al caso de cambios múltiples de RHS simultáneamente, esto es presentado en la aplicación siguiente.

Ejemplo Numérico 3: Como nuestro ejemplo numérico para cambios de RHS múltiples simultáneos, considere el (Problema del Carpintero) the Carpenter's Problem:

Maximice 5 X1 + 3 X2

Sujeto a:
2 X1 + X2 £ 40 restricción de labor
X1 + 2 X2 £ 50 restricción de materiales
y ambos X1, X2 son no negativos.

La tabla óptima simplex para este problema es:

BVS	X1	X2	S1	S2	RHS
X1	1	0	2/3	-1/3	10
X2	0	1	-1/3	2/3	20
Cj	0	0	-7/3	-1/3

Ahora considere, la versión RHS paramétrica de este problema:

Maximice 5 X1 + 3 X2

Sujeto a:
2 X1 + X2 £ 40 + r1
X1 + 2 X2 £ 50 + r2
y ambos X1, X2 son no negativos.

Siguiendo el mismo procedimiento pero alterando ambos valores de RHS por r1, y r2 respectivamente, usando las columnas de holgura/excedente de la tabla óptima, uno obtiene los RHS paramétrico siguiente directamente.

BVS	X1	X2	S1	S2	Parametric RHS
X1	1	0	2/3	-1/3	10 + 2r1/3 -r2/3
X2	0	1	-1/3	2/3	20-r1/3 + 2r2/3
Cj	0	0	-7/3	-1/3

Note que alterando ambos RHS por r1 y r2 respectivamente, uno obtiene la región de sensibilidad general para cambios simultáneos, independientes (o dependientes) de ambos valores RHS como sigue:

{r1, r2 | 10 + 2r1/3 - r2/3³ 0, 20 -r1/3 + 2r2/3³0}

La siguiente región representa el análisis de sensibilidad general para los valores de RHS del (Problema del Carpintero) the Carpenter's Problem:

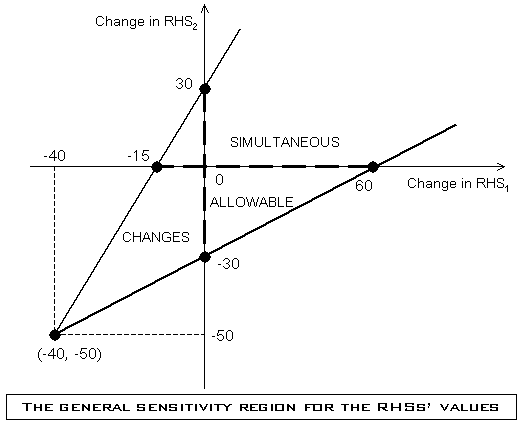
Note que, la región de sensibilidad contiene el origen que corresponde al problema nominal. Además el vértice del rango de sensibilidad está en el punto (-40,-50) donde ambos valores de RHS desaparecen.

---

Análisis de los Modelos de PL con Restricciones de Igualdad

Ejemplo Numérico 4: Considere el problema de PL siguiente con una restricción de igualdad:

Max 5X1 + 3X2

Sujeto a:
2X1 + X2 £ 40
X1 + X2 = 26
y ambos X1 y X2 son no negativos.

Convirtiendo las restricciones de igualdad en dos restricciones de desigualdad, tenemos el problema equivalente siguiente:

Max 5X1+ 3X2

Sujeto a:

2X1 + X2 £ 40
X1 + X2 £ 26
X1 + X2 ³ 26
y X1, X2 ³ 0.

Introduciendo variables de holgura/excedente para convertir las restricciones en forma de igualdad, tenemos:

Max 5X1+ 3X2

Sujeto a:

2X1 + X2 + S1 = 40
X1 + X2 + S2 = 26
X1 + X2 - S3 = 26
y todas las variables son no negativas.

Las Herramientas del Análisis de Sensibilidad: las herramientas de análisis de sensibilidad siguientes son también asequibles usando (la herramienta de Optimización Lineal con Análisis de Sensibilidad JavaScript)Linear Optimization with Sensitivity Analysis Tools JavaScript.

La Estrategia Óptima para las Variables de Decisión son: X1 = 14, X2 = 12. Uno puede encontrar el valor de la variable de holgura/excedente Si para la restricción i, substituyendo la estrategia óptima en la restricción i^ésima. Por ejemplo, el excedente S3 = 26 - 14 + 12 = 0. Ya que las variables no básicas son siempre iguales a cero, para este problema, ambas variables de holgura S1 y S2 son cero.

La Matriz de Variables No-básica B_NB es:

S1	S2
1	-1
0	1
-1	2

The C_j El Vector de la Fila Cj es:

X1	X2	S1	S2	S3
0	0	-2	-1	0

Los elementos de Cj corresponden a las Variables de Decisión en la misma secuencia en que ellos aparecieron en la función objetivo, luego seguidos de las Variables de holgura/excedente. El elemento Cj para las Variables Básicas es siempre igual a cero.

Note que el número de elementos cero en el vector de fila Cj deben ser igual al número de restricciones, de otra manera el problema podría tener soluciones múltiples, y por lo tanto cualquier resultado del análisis de sensibilidad podría ser no fiable.

El Vector de Columna RHS es:

RHS
14
0
12

Los elementos de RHS son los valores de las Variables Básica. Note que si algún elemento en la columna de vector RHS es cero, entonces la solución óptima podría ser una solución degenerada, por lo tanto cualquier resultado del análisis de sensibilidad podría ser no fiable.

Por lo tanto, la tabla óptima con RHS paramétrico para este problema es:

BVS	X1	X2	S1	S2	S3	Parametric RHS
X1	1	0	1	-1	0	14 + (1)r1+ (-1 - 0)r2	= 14 + r1 - r2
S3	0	0	0	1	1	0 + 0r1 + (1 - 1)r2	= 0
X2	0	1	-1	2	0	12 + (-1)r1 +(2 - 0)r2	= 12 - r1 + 2r2
Cj	0	0	-2	-1	0

Note que el precio sombra para el RHS de la restricción de igualdad es la suma de dos precios sombra de restricciones equivalentes, es decir 1 + 0 = 1, obtenible del vector de fila Cj.

El valor óptimo paramétrico es 5X1 + 3X2 = 5 (14 + r1 - r2) + 3 (12 - r1 + 2r2) = 106 + 2r1 + r2. Además, los coeficientes de r1 y r2 son los precios sombra de la primera y la segunda restricción del valor de RHS, como es esperado.

Cambiando todo RHS paramétrico a ³ 0, como antes, da el aumento aceptable y la disminución aceptable para cada valor de RHS. Habiendo construido la región de sensibilidad general, todos los otros tipos de análisis de sensibilidad, como el Paramétrico y el análisis de Tolerancia, puede ser realizado fácilmente.

Cálculo de la Matriz de B-inverso Generalizada: Note que, el RHS paramétrico óptimo contiene información útil. Por ejemplo los coeficientes de los parámetros constituyen lo que es conocido como laMatriz Inversa Base , es decir, el b-1, donde la B-matriz de base es la matriz de los coeficientes de la variable básica en el conjunto de restricción.

Ejemplo Numérico 5: Para el ejemplo numérico 4, la matriz inversa de base generalizada (no es necesariamente una matriz cuadrada) es:

r1	r2
1	-1
0	0
-1	2

Ya que la multiplicación de la matriz B^-1 por el vector de columna RHS es el RHS óptimo. Entonces, uno puede verificar el hecho de que los coeficientes de los parámetros constituyen en efecto la matriz inversa de base. El vector de columna RHS es:

RHS
40
26

La multiplicación del B^-1 por el vector de columna RHS da:

Optimal RHS
14
0
12

Este resultado fue esperado.

---

Un Nuevo Enfoque Alternativo
Basado en la Solución Óptima

Conociendo la solución óptima única para las variables de decisión usando cualquier solucionista de PL, uno puede construir el análisis de sensibilidad simultáneamente para todos los valores de RHS de la siguiente forma: Suponga que el problema de PL tiene n numero de variables de decisión y m restricciones incluyendo las condiciones de no-negatividad (si alguna).

Paso 1: Identifique las restricciones n que son obligatorias en la solución óptima. Si hay más que el número n de restricciones obligatorias, entonces el problema es degenerado, lo que significa que el análisis de sensibilidad no es aplicable.

Paso 2: Construya el RHS paramétrico de las restricciones, excluyendo las condiciones de no-negatividad (si alguna).

Paso 3: Solucione el sistema paramétrico de ecuaciones consistente de las restricciones obligatorias. Esto proporciona la solución óptima paramétrica.

Paso 4: Para construir el análisis de sensibilidad simultáneo, inserte la solución obtenida en el Paso 3, en todas las otras restricciones paramétricas, incluyendo la condición de no-negatividad (si alguna).

El ejemplo siguiente ilustra el procedimiento anterior.

Ejemplo Numérico 6: Considere el problema del ejemplo numérico 2, es decir, después del problema de PL:

Max -X1 + 2X2
sujeto a:
X1 + X2 ³ 2,
-X1 + X2 ³ 1,
X2 £ 3,
X1 ³ 0,
X2 ³ 0.

Hay n = 2 variables de decisión, y m = 5 restricción.

Paso 1: Identifique las restricciones n = 2 que son obligatorias en la solución óptima dada (X1 = 0, X2 = 3). Las restricciones obligatorias son las restricciones número 3 y 4, que son X2 £ 3, y X1 ³ 0.

Paso 2: Construya el RHS paramétrico de las restricciones, excluyendo las condiciones de no-negatividad, es decir,

X1 + X2 ³ 2 + r1,
-X1 + X2 ³ 1 + r2,
X2 £ 3 + r3,
X1 ³ 0,
X2 ³ 0.

Paso 3: Solucione el sistema paramétrico de ecuaciones consistente en las restricciones obligatorias, es decir, solucionando:

X2 = 3 + r3,
X1 = 0,

Esta es la solución óptima paramétrica.

Paso 4: El análisis de sensibilidad simultáneo es obtenido insertando esta solución en todas las otras restricciones paramétricas, incluyendo la condición de no-negativa (si alguna). Es decir insertando X1 = 0 y X2 = 3 + r3 en:

X1 + X2 ³ 2 + r1,
-X1 + X2 ³ 1 + r2,
X2 ³ 0.

Con una pequeña álgebra, el análisis de sensibilidad simultáneo para cambios simultáneos de cualquier número de valores de RHS es el conjunto siguiente:

{r1, r2, r3 | 1- r2 + r3 ³ 0, 2 - r2 + r3 ³ 0, 3 + r3 ³ 0}

---

Sensibilidad de los Coeficientes de la Función Objetiva
La estrategia óptima para las variables de decisión permanece sin alterar

El problema es encontrar un rango para cada coeficiente de coste C (j), de variable Xj, tal que la solución óptima actual (es decir punto extremo) permanece óptima.

Tenemos que construir la versión paramétrica de la última fila en la tabla óptima realizando las operaciones de matriz siguientes:

[Coeficientes paramétricos actuales] - [los coeficientes paramétricos de la Variable Básica como estos aparecieron en la tabla óptima].[El contenido de la tabla óptima]

Ejemplo Numérico 7: Como nuestro ejemplo numérico, usaremos el problema de PL analizado en el ejemplo 2:

Max -X1 + 2X2
sujeto a:
X1 + X2 ³ 2,
-X1 + X2 ³ 1,
X2 £ 3,
y X1, X2 ³ 0.

Introduciendo variables de holgura/excedente para convertir las restricciones en forma de igualdad, tenemos:

X1 + X2 - S1 = 2,
-X1 + X2 - S2 = 1,
X2 + S3 = 3,
y todas las variables son no negativas.

La tabla óptima para este problema es:

BVS	X1	X2	S1	S2	S3	RHS
S2	1	0	0	1	1	2
X2	0	1	0	0	1	3
S1	-1	0	1	0	1	1
Cj	-1	0	0	0	-2

Considere, por ejemplo cambiando C (1) =-1, a -1 + c1, la versión paramétrica de la última fila en la tabla óptima es:

[-1+c1, 2, 0, 0, 0]	-	[0, 2, 0]	| 1 0 0 1 1 |
			| 0 1 0 0 1 |
			|-1 0 1 0 1 |

Multiplicando la segunda matriz por la tercera, y después de alguna álgebra tenemos:

[-1+c1, 2, 0, 0, 0] - [0, 2, 0, 0, 2] = [-1+c1, 0, 0, 0, -2]

Para comprobar nuestros cálculos, si ponemos c1 = 0, deberíamos obtener la última fila de nuestra tabla óptima actual.

Para mantenerse siendo óptima, todos los elementos de la versión paramétrica de la última fila de la tabla óptima deben ser £ 0, tenemos:

-1 + c1 £ 0. Esto da c1 £ 1. Por lo tanto el aumento aceptable es 1, mientras la disminución aceptable es tanto como usted quiera.

Del mismo modo, el rango de sensibilidad para C(2) es el siguiente: cambiando C(2) = 2, a 2 + c2, la versión paramétrica de la última fila en la tabla óptima es:

[-1, 2+c2, 0, 0, 0]	-	[0, 2+c2, 0]	| 1 0 0 1 1 |
			| 0 1 0 0 1 |
			|-1 0 1 0 1 |

Multiplicando la segunda matriz por la tercera, y después de alguna álgebra tenemos:

[-1, 2+c2, 0, 0, 0] - [0, 2+c2, 0, 2+c2] = [-1, 0, 0, 0, -2-c2]

Para comprobar nuestros cálculos, si ponemos c2 = 0, deberíamos obtener la última fila de nuestra tabla óptima actual.

Poniendo todos los elementos de la versión paramétrica de la última fila de la tabla óptima a £ 0, tenemos:

-2 - c2 £ 0. Esto da c2 ³ -2. Por lo tanto la disminución aceptable es 2, mientras el aumento aceptable es tanto como usted quiera.

Si usted no esta acostumbrado a trabajar con matrices grandes, una alternativa al procedimiento anterior es construir el rango de sensibilidad para el RHS del problema dual.

Ejemplo Numérico 8: Como otro ejemplo, considere (el Problema del Carpintero) the Carpenter's Problem:

Max 5 X1 + 3 X2

Sujeto a:
2 X1 + X2 £ 40 restricción de trabajo
X1 + 2 X2 £ 50 restricción de material
y ambos X1, X2 son no negativos.

Claramente, el cambio de la ganancia de cada producto cambia la inclinación de la función objetivo del valor-iso. Para pequeños cambios la solución óptima permanece en el mismo punto extremo. Para cambios más grandes la solución óptima se mueve a otro punto. Entonces nosotros tenemos que modificar la formación y solucionar un nuevo problema.

Después del mismo procedimiento del ejemplo 7, pero alterando ambos coeficientes de coste por c1 y c2 respectivamente, uno obtiene la región de sensibilidad general para cambio simultáneo, independiente (o dependiente) de ambos coeficientes de coste.

Por otro lado, uno puede construir la región de sensibilidad de RHS para (El problema dual para el Problema del Carpintero) The dual problem for the Carpenter's Problem es:

Minimice 40 U1 + 50 U2
Sujeto a:
2U1 + 1U2 ³ 5 Ingresos Netos de una mesa
1U1 + 2U2 ³ 3 Ingresos Netos de una silla
y U1, U2 son no negativos.

Implementando cualquier algoritmo de solución presentado en la página Algoritmos de Solución Estratégicos No-Artificiales (Artificial-free Strategic Solution Algorithms), uno obtiene la tabla óptima simplex siguiente:

BVS	U1	U2	S1	S2	RHS
U2	0	1	1/3	-2/3	1/3
U1	1	0	-2/3	1/3	7/3
Cj	0	0	-10	-20

La tabla óptima muestra que la solución óptima es U1 = $7/3 y U2 = $1/3 con el valor óptimo de 110 dólares como esperado.

La versión RHS paramétrica de este problema es:

Minimice 40 U1 + 50 U2
Sujeto a:
2U1 + 1U2 ³ 5 + c1
1U1 + 2U2 ³ 3 + c2
y U1, U2 son no negativos.

Después del mismo procedimiento pero alterando tanto los coeficientes de coste c1, como c2 respectivamente, considerando las columnas de holgura/excedente en la tabla óptima, uno obtiene el RHS paramétrico siguiente.

BVS	U1	U2	S1	S2	Parametric RHS
U2	0	1	1/3	-2/3	1/3 -c1/3 +2c2/3
U1	1	0	-2/3	1/3	7/3 + 2c1/3 - c2/3
Cj	0	0	-10	-20

Por lo tanto, perturbando ambos coeficiente de coste en el Problema del Carpintero por c1 y c2 respectivamente, uno obtiene la región de sensibilidad general para cambio simultáneo, independiente (o dependiente) de ambos coeficientes de coste como sigue:

{c1, c2 | 1/3 - c1/3 + 2c2/3³ 0, 7/3 + 2c1/3 - c2/3³0}

La siguiente región representa el análisis de sensibilidad general para los valores de los coeficientes de coste del Problema del Carpintero:

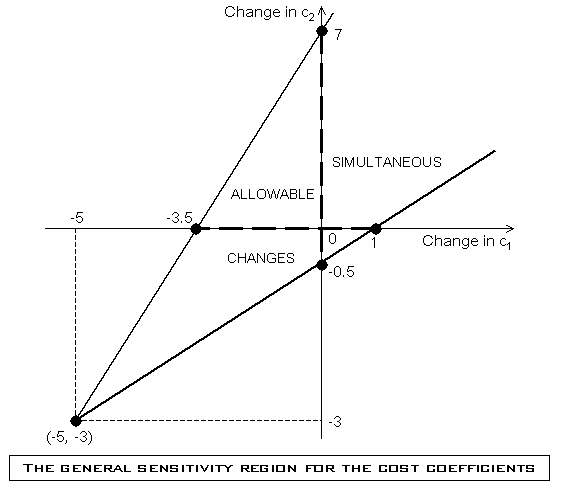
Note que, la región de sensibilidad contiene el origen que corresponde al problema nominal. Además el vértice del rango de sensibilidad está en el punto (-5,-3) donde ambos coeficientes de coste desaparecen.

Habiendo construido la región de sensibilidad general tanto para el RHS como para los Coeficientes de Coste, todos los otros tipos del análisis de sensibilidad, como el Paramétrico o el análisis de Tolerancia puede ser realizado fácilmente.

---

Un Nuevo Enfoque Alternativo
Basado en la Solución Óptima Dual

Conociendo la solución óptima dual única para el problema dual usando a cualquier solucionista de PL, uno puede construir el análisis de sensibilidad simultáneo para todo coeficiente de la función objetivo del problema primal como es presentado a continuación.

Paso 0: Construya y solucione el problema dual. Suponga que el problema dual tiene n variables de decisión y m restricciones incluyendo las condiciones de no-negatividad (si alguna).

Paso 1: Identifique las restricciones n que son obligatorias en la solución óptima. Si hay más que las restricciones obligatorias n, entonces el problema primal puede tener soluciones múltiples, lo que significa que el análisis de sensibilidad no es aplicable.

Paso 2: construya el RHS paramétrico de las restricciones, excluyendo las condiciones de no-negatividad (si alguna).

Paso 3: Solucione el sistema paramétrico de ecuaciones consistente de las restricciones obligatorias. Esto proporciona la solución óptima paramétrica.

Paso 4: Para construir el análisis de sensibilidad simultáneo, inserte la solución obtenida en el Paso 3, en todas las otras restricciones paramétricas, incluyendo la condición de no-negatividad (si alguna).

El ejemplo siguiente ilustra el procedimiento anterior.

Ejemplo Numérico 9: Considere el problema del ejemplo numérico 2, es decir, después del problema de PL:

Max -X1 + 2X2
sujeto a:
X1 + X2 ³ 2,
-X1 + X2 ³ 1,
X2 £ 3,
X1 ³ 0,
X2 ³ 0.

Paso 0: Construya el problema dual:

Min -U1 - U2 + 3U3
sujeto a:
-U1 + U2 ³ -1,
-U1 - U2 + U3 ³ 2,
U1 ³ 0,
U2 ³ 0,
U3 ³ 0.

La solución óptima es U1 = 0, U2 = 0, U3 = 2. El problema dual tiene n = 3 variables de decisión y m = 5 restricciones incluyendo las condiciones de no-negatividad (si alguna).

Paso 1: Identifique las restricciones n = 3 que son obligatorias en la solución óptima:

-U1 - U2 + U3 ³ 2,
U1 ³ 0,
U2 ³ 0,

Paso 2: construya el RHS paramétrico de las restricciones, excluyendo las condiciones de no-negatividad (si alguna):

-U1 + U2 ³ -1 + c1,
-U1 - U2 + U3 ³ 2 + c2,
U1 ³ 0,
U2 ³ 0,
U3 ³ 0.

Paso 3: Solucione el sistema paramétrico de ecuaciones consistente de las restricciones obligatorias,

-U1 - U2 + U3 ³ 2 + c2,
U1 ³ 0,
U2 ³ 0.

Esto proporciona la solución óptima paramétrica:

U1 = 0,
U2 = 0,
U3 = 2 + c2

Paso 4: el análisis de sensibilidad simultáneo para los coeficientes de la función objetiva para el problema primal es obtenido insertando esta solución en todas las otras restricciones paramétricas, incluyendo la condición de no-negatividad (si alguna). Es decir haciendo U1 = 0, U2 = 0, y U3 = 2 + c2 en:

-U1 + U2 ³ -1 + c1,
U3 ³ 0.

Con una pequeña álgebra, el análisis de sensibilidad simultáneo para cambios simultáneos de coeficientes de la función objetiva para el problema primal es el conjunto siguiente:

{c1, c2 | c1 £ 1, c2 ³ -2}

---

La actualización de la Solución Actual para Pequeños Cambios de la Matriz de Tecnología A

Cambio de Un elemento en la Matriz de Tecnología A: sea la matriz base actual denotada por B con su inverso denotado por B^-1. Sean también d_ij y d_ij^-1 las denotaciones del elemento en la fila de i-ésima y la columna j-ésima de B y B^-1, respectivamente. Si un elemento en fila i y columna j en la matriz B es cambiado por d, entonces el nuevo B^-1 puede ser obtenido actualizando el viejo como sigue:

B_nuevo^-1 = B^-1 - d [B^-1E_iE_j^TB^-1] / [1 + d_ji^-1d]

Donde E_i es un vector de fila de ceros con uno en la posición i-ésima y E_j^T denota la transpuesta del vector E_j.

La solución actualizada es: X = B_nuevo^-1.b

Visite también:
Análisis de Sensibilidad

Referencias y Lecturas Adicionales:
Adler I., and R. Monteiro, A geometric view of parametric linear programming, Algorithmica, 8, 161-176, 1992.
Arsham H., Perturbation analysis of general LP models: A unified approach to sensitivity, parametric tolerance, and more-for-less analysis, Mathematical and Computer Modelling, 12, 1437-1446, 1990.
Aucamp D., and D. Steinberg, The computation of shadow price in linear programming, Journal of Operational Research Society, 33, 557-565, 1982.
Berkelaar A. , C. Roos, and T. Terlaky, The optimal set and optimal partition approach to linear and quadratic programming. Chapter 6 in Advances in Sensitivity Analysis and Parametric Programming, T. Gal and H. J. Greenberg, eds., Kluwer Academic Publishers, 1997.
Borges A., and C. Antunes, A visual interactive tolerance approach to sensitivity analysis in MOLP, European Journal of Operational Research, 142, 357-381, 2002.
Evans J., and N. Baker, Degeneracy and the (mis)interpretation of sensitivity analysis in linear programming, Decision Sciences, 13, 348-354, 1982.
Gass S., and S. Vinjamuri, Cycling in linear programming problems, Computers & Operations Research, 31, 303-311, 2004.
Greenberg H., Simultaneous primal-dual right-hand-side sensitivity analysis from a strictly complementary solution of a linear program, SIAM Journal of Optimization, 10, 427-442, 2000.
Jansen B., Sensitivity analysis in linear programming: just be careful!, European Journal of Operational Research, 101, 15-28, 1997.
Yildirim E., A unifying optimal partition approach to sensitivity analysis in conic optimization, Journal of Optimization Theory and Applications, 122, 405-423, 2004.

---

Declaración de derechos de propiedad intelectual: El uso legítimo, según las pautas de 1996 guías de consulta justas del uso para los multimedia educativos, de los materiales presentados en este sitio Web está permitido para propósitos educativos no comerciales.
Este sitio puede duplicarse, intacto con esta declaración, en cualquier servidor de acceso público y puede vincularse a cualquier otra página Web. Todos los archivos se encuentran disponibles en http://home.ubalt.edu/ntsbarsh/Business-stat para el duplicado.

Agradecería recibir comentarios, sugerencias e inquietudes por e-mail Gracias.

Professor Hossein Arsham   

---

Este sitio fue lanzado en el 25/02/1994, y sus materiales intelectuales han sido revisados a fondo anualmente. La versión actual es la 8 ^va Edición. Todos los enlaces externos son revisados una vez al mes.

---

De vuelta a:

Dr Arsham's Home Page

---