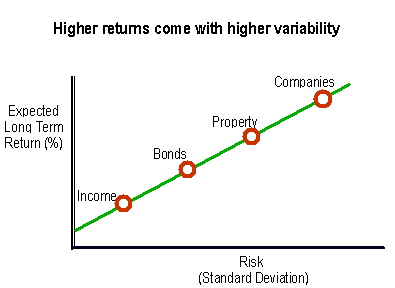
Analysis of Risky Decisions
To search the site, try Edit | Find in page [Ctrl + f]. Enter a word or phrase in the dialogue box, e.g. "risk " or "utility " If the first appearance of the word/phrase is not what you are looking for, try Find Next.
MENU
- Introduction & Summary
- Probabilistic Modeling: From Data to a Decisive Knowledge
- Decision Analysis: Making Justifiable, Defensible Decisions
- Elements of Decision Analysis Models
- Decision Making Under Pure Uncertainty: Materials are presented in the context of Financial Portfolio Selections.
- Limitations of Decision Making under Pure Uncertainty
- Coping with Uncertainties
- Decision Making Under Risk: Presentation is in the context of Financial Portfolio Selections under risk.
- Making a Better Decision by Buying Reliable Information: Applications are drawn from Marketing a New Product.
- Decision Tree and Influence Diagram
- Why Managers Seek the Advice From Consulting Firms
- Revising Your Expectation and its Risk
- Determination of the Decision-Maker's Utility
- Utility Function Representations with Applications
- A Classification of Decision Maker's Relative Attitudes Toward Risk and Its Impact
- The Discovery and Management of Losses
- Risk: The Four Letters Word
- Decision's Factors-Prioritization & Stability Analysis
- Optimal Decision Making Process
- JavaScript E-labs Learning Objects
- A Critical Panoramic View of Classical Decision Analysis
- Exercise Your Knowledge to Enhance What You Have Learned (PDF)
- Appendex: A Collection of Keywords and Phrases
Companion Sites:
- Business Statistics
- Success Science
- Leadership Decision Making
- Linear Programming (LP) and Goal-Seeking Strategy
- Linear Optimization Software to Download
- Artificial-variable Free LP Solution Algorithms
- Integer Optimization and the Network Models
- Tools for LP Modeling Validation
- The Classical Simplex Method
- Zero-Sum Games with Applications
- Computer-assisted Learning Concepts and Techniques
- Linear Algebra and LP Connections
- From Linear to Nonlinear Optimization with Business Applications
- Construction of the Sensitivity Region for LP Models
- Zero Sagas in Four Dimensions
- Systems Simulation
- Business Keywords and Phrases
- Compendium of Web Site Review
- Collection of JavaScript E-labs Learning Objects
- Decision Science Resources
- Compendium of Web Site Review
Introduction & Summary
Rules of thumb, intuition, tradition, and simple financial analysis are often no longer sufficient for addressing such common decisions as make-versus-buy, facility site selection, and process redesign. In general, the forces of competition are imposing a need for more effective decision making at all levels in organizations.Decision analysts provide quantitative support for the decision-makers in all areas including engineers, analysts in planning offices and public agencies, project management consultants, manufacturing process planners, financial and economic analysts, experts supporting medical/technological diagnosis, and so on and on.
Progressive Approach to Modeling: Modeling for decision making involves two distinct parties, one is the decision-maker and the other is the model-builder known as the analyst. The analyst is to assist the decision-maker in his/her decision-making process. Therefore, the analyst must be equipped with more than a set of analytical methods.
Specialists in model building are often tempted to study a problem, and then go off in isolation to develop an elaborate mathematical model for use by the manager (i.e., the decision-maker). Unfortunately the manager may not understand this model and may either use it blindly or reject it entirely. The specialist may feel that the manager is too ignorant and unsophisticated to appreciate the model, while the manager may feel that the specialist lives in a dream world of unrealistic assumptions and irrelevant mathematical language.
Such miscommunication can be avoided if the manager works with the specialist to develop first a simple model that provides a crude but understandable analysis. After the manager has built up confidence in this model, additional detail and sophistication can be added, perhaps progressively only a bit at a time. This process requires an investment of time on the part of the manager and sincere interest on the part of the specialist in solving the manager's real problem, rather than in creating and trying to explain sophisticated models. This progressive model building is often referred to as the bootstrapping approach and is the most important factor in determining successful implementation of a decision model. Moreover the bootstrapping approach simplifies otherwise the difficult task of model validating and verification processes.
What is a System: Systems are formed with parts put together in a particular manner in order to pursuit an objective. The relationship between the parts determines what the system does and how it functions as a whole. Therefore, the relationship in a system are often more important than the individual parts. In general, systems that are building blocks for other systems are called subsystems
The Dynamics of a System: A system that does not change is a static (i.e., deterministic) system. Many of the systems we are part of are dynamic systems, which are they change over time. We refer to the way a system changes over time as the system's behavior. And when the system's development follows a typical pattern we say the system has a behavior pattern. Whether a system is static or dynamic depends on which time horizon you choose and which variables you concentrate on. The time horizon is the time period within which you study the system. The variables are changeable values on the system.
In deterministic models, a good decision is judged by the outcome alone. However, in probabilistic models, the decision-maker is concerned not only with the outcome value but also with the amount of risk each decision carries
As an example of deterministic versus probabilistic models, consider the past and the future: Nothing we can do can change the past, but everything we do influences and changes the future, although the future has an element of uncertainty. Managers are captivated much more by shaping the future than the history of the past.
Uncertainty is the fact of life and business; probability is the guide for a "good" life and successful business. The concept of probability occupies an important place in the decision-making process, whether the problem is one faced in business, in government, in the social sciences, or just in one's own everyday personal life. In very few decision making situations is perfect information - all the needed facts - available. Most decisions are made in the face of uncertainty. Probability enters into the process by playing the role of a substitute for certainty - a substitute for complete knowledge.
Probabilistic Modeling is largely based on application of statistics for probability assessment of uncontrollable events (or factors), as well as risk assessment of your decision. The original idea of statistics was the collection of information about and for the State. The word statistics is not derived from any classical Greek or Latin roots, but from the Italian word for state. Probability has a much longer history. Probability is derived from the verb to probe meaning to "find out" what is not too easily accessible or understandable. The word "proof" has the same origin that provides necessary details to understand what is claimed to be true.
Probabilistic models are viewed as similar to that of a game; actions are based on expected outcomes. The center of interest moves from the deterministic to probabilistic models using subjective statistical techniques for estimation, testing, and predictions. In probabilistic modeling, risk means uncertainty for which the probability distribution is known. Therefore risk assessment means a study to determine the outcomes of decisions along with their probabilities.
Decision-makers often face a severe lack of information. Probability assessment quantifies the information gap between what is known, and what needs to be known for an optimal decision. The probabilistic models are used for protection against adverse uncertainty, and exploitation of propitious uncertainty.
Difficulty in probability assessment arises from information that is scarce, vague, inconsistent, or incomplete. A statement such as "the probability of a power outage is between 0.3 and 0.4" is more natural and realistic than their "exact" counterpart such as "the probability of a power outage is 0.36342."
It is a challenging task to compare several courses of action and then select one action to be implemented. At times, the task may prove too challenging. Difficulties in decision making arise through complexities in decision alternatives. The limited information-processing capacity of a decision-maker can be strained when considering the consequences of only one course of action. Yet, choice requires that the implications of various courses of action be visualized and compared. In addition, unknown factors always intrude upon the problem situation and seldom are outcomes known with certainty. Almost always, an outcome depends upon the reactions of other people who may be undecided themselves. It is no wonder that decision-makers sometimes postpone choices for as long as possible. Then, when they finally decide, they neglect to consider all the implications of their decision.
Emotions and Risky Decision: Most decision makers rely on emotions in making judgments concerning risky decisions. Many people are afraid of the possible unwanted consequences. However, do we need emotions in order to be able to judge whether a decision and its concomitant risks are morally acceptable. This question has direct practical implications: should engineers, scientists and policy makers involved in developing risk regulation take the emotions of the public seriously or not? Even though emotions are subjective and irrational (or a-rational), they should be a part of the decision making process since they show us our preferences. Since emotions and rationality are not mutually exclusive, because in order to be practically rational, we need to have emotions. This can lead to an alternative view about the role of emotions in risk assessment: emotions can be a normative guide in making judgments about morally acceptable risks.
Most people often make choices out of habit or tradition, without going through the decision-making process steps systematically. Decisions may be made under social pressure or time constraints that interfere with a careful consideration of the options and consequences. Decisions may be influenced by one's emotional state at the time a decision is made. When people lack adequate information or skills, they may make less than optimal decisions. Even when or if people have time and information, they often do a poor job of understanding the probabilities of consequences. Even when they know the statistics; they are more likely to rely on personal experience than information about probabilities. The fundamental concerns of decision making are combining information about probability with information about desires and interests. For example: how much do you want to meet her, how important is the picnic, how much is the prize worth?
Business decision making is almost always accompanied by conditions of uncertainty. Clearly, the more information the decision maker has, the better the decision will be. Treating decisions as if they were gambles is the basis of decision theory. This means that we have to trade off the value of a certain outcome against its probability.
To operate according to the canons of decision theory, we must compute the value of a certain outcome and its probabilities; hence, determining the consequences of our choices.
The origin of decision theory is derived from economics by using the utility function of payoffs. It suggests that decisions be made by computing the utility and probability, the ranges of options, and also lays down strategies for good decisions:
This Web site presents the decision analysis process both for public and private decision making under different decision criteria, type, and quality of available information. This Web site describes the basic elements in the analysis of decision alternatives and choice, as well as the goals and objectives that guide decision making. In the subsequent sections, we will examine key issues related to a decision-makers preferences regarding alternatives, criteria for choice, and choice modes.
Objectives are important both in identifying problems and in evaluating alternative solutions. Evaluating alternatives requires that a decision-makers objectives be expressed as criterion that reflects the attributes of the alternatives relevant to the choice.
The systematic study of decision making provides a framework for choosing courses of action in a complex, uncertain, or conflict-ridden situation. The choices of possible actions, and the prediction of expected outcomes, derive from a logical analysis of the decision situation.
A Possible Drawback in the Decision Analysis Approach: You might have already noticed that the above criteria always result in selection of only one course of action. However, in many decision problems, the decision-maker might wish to consider a combination of some actions. For example, in the Investment problem, the investor might wish to distribute the assets among a mixture of the choices in such a way to optimize the portfolio's return. Visit the Game Theory with Applications Web site for designing such an optimal mixed strategy.
Further Readings:
Arsham H., A Markovian model of consumer buying behavior and optimal advertising pulsing policy, Computers and Operations Research, 20(2), 35-48, 1993.
Arsham H., A stochastic model of optimal advertising pulsing policy, Computers and Operations Research, 14(3), 231-239, 1987.
Ben-Haim Y., Information-gap Decision Theory: Decisions Under Severe Uncertainty, Academic Press, 2001.
Golub A., Decision Analysis: An Integrated Approach, Wiley, 1997.
Goodwin P., and G. Wright, Decision Analysis for Management Judgment, Wiley, 1998.
van Gigch J., Metadecisions: Rehabilitating Epistemology, Kluwer Academic Publishers, 2002.
Wickham Ph., Strategic Entrepreneurship: A Decision-making Approach to New Venture Creation and Management, Pitman, 1998.
Probabilistic Modeling: From Data to a Decisive Knowledge
Knowledge is what we know well. Information is the communication of knowledge. In every knowledge exchange, there is a sender and a receiver. The sender make common what is private, does the informing, the communicating. Information can be classified as explicit and tacit forms. The explicit information can be explained in structured form, while tacit information is inconsistent and fuzzy to explain. Know that data are only crude information and not knowledge by themselves.
Data is known to be crude information and not knowledge by itself. The sequence from data to knowledge is: from Data to Information, from Information to Facts, and finally, from Facts to Knowledge. Data becomes information, when it becomes relevant to your decision problem. Information becomes fact, when the data can support it. Facts are what the data reveals. However the decisive instrumental (i.e., applied) knowledge is expressed together with some statistical degree of confidence.
Fact becomes knowledge, when it is used in the successful completion of a decision process. Once you have a massive amount of facts integrated as knowledge, then your mind will be superhuman in the same sense that mankind with writing is superhuman compared to mankind before writing. The following figure illustrates the statistical thinking process based on data in constructing statistical models for decision making under uncertainties.
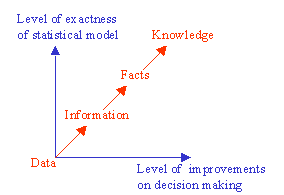
The above figure depicts the fact that as the exactness of a statistical model increases, the level of improvements in decision-making increases. That's why we need probabilistic modeling. Probabilistic modeling arose from the need to place knowledge on a systematic evidence base. This required a study of the laws of probability, the development of measures of data properties and relationships, and so on.
Statistical inference aims at determining whether any statistical significance can be attached that results after due allowance is made for any random variation as a source of error. Intelligent and critical inferences cannot be made by those who do not understand the purpose, the conditions, and applicability of the various techniques for judging significance.
Knowledge is more than knowing something technical. Knowledge needs wisdom. Wisdom is the power to put our time and our knowledge to the proper use. Wisdom comes with age and experience. Wisdom is the accurate application of accurate knowledge and its key component is to knowing the limits of your knowledge. Wisdom is about knowing how something technical can be best used to meet the needs of the decision-maker. Wisdom, for example, creates statistical software that is useful, rather than technically brilliant. For example, ever since the Web entered the popular consciousness, observers have noted that it puts information at your fingertips but tends to keep wisdom out of reach.
Considering the uncertain environment, the chance that "good decisions" are made increases with the availability of "good information." The chance that "good information" is available increases with the level of structuring the process of Knowledge Management. One may ask, "What is the use of decision analysis techniques without the best available information delivered by Knowledge Management?" The answer is: one can not make responsible decisions until one possess enough knowledge. However, for private decisions one may rely on, e.g., the psychological motivations, as discusses under "Decision Making Under Pure Uncertainty" in this site. Moreover, Knowledge Management and Decision Analysis are indeed interrelated since one influences the other, both in time, and space. The notion of "wisdom" in the sense of practical wisdom has entered Western civilization through biblical texts. In the Hellenic experience this kind of wisdom received a more structural character in the form of philosophy. In this sense philosophy also reflects one of the expressions of traditional wisdom.
Making decisions is certainly the most important task of a manager and it is often a very difficult one. This site offers a decision making procedure for solving complex problems step by step.
The Decision-Making Process: Unlike the deterministic decision-making process, in the decision making process under uncertainty the variables are often more numerous and more difficult to measure and control. However, the steps are the same. They are:
- Simplification
- Building a decision model
- Testing the model
- Using the model to find the solution
- It is a simplified representation of the actual situation
- It need not be complete or exact in all respects
- It concentrates on the most essential relationships and ignores the less essential ones.
- It is more easily understood than the empirical situation and, hence, permits the problem to be more readily solved with minimum time and effort.
- It can be used again and again for like problems or can be modified.
Fortunately the probabilistic and statistical methods for analysis and decision making under uncertainty are more numerous and powerful today than even before. The computer makes possible many practical applications. A few examples of business applications are the following:
- An auditor can use random sampling techniques to audit the account receivable for client.
- A plant manager can use statistic quality control techniques to assure the quality of his production with a minimum of testing or inspection.
- A financial analyst may use regression and correlation to help understand the relationship of a financial ratio to a set of other variables in business.
- A market researcher may use test of significant to accept or reject the hypotheses about a group of buyers to which the firm wishes to sell a particular product.
- A sale manager may use statistical techniques to forecast sales for the coming year.
Further Readings:
Berger J., Statistical Decision Theory and Bayesian Analysis, Springer, 1978.
Corfield D., and J. Williamson, Foundations of Bayesianism, Kluwer Academic Publishers, 2001. Contains Logic, Mathematics, Decision Theory, and Criticisms of Bayesianism.
Grünig R., Kühn, R.,and M. Matt, (Eds.), Successful Decision-Making: A Systematic Approach to Complex Problems, Springer, 2005. It is intended for decision makers in companies, in non-profit organizations and in public administration.
Lapin L., Statistics for Modern Business Decisions, Harcourt Brace Jovanovich, 1987.
Lindley D., Making Decisions, Wiley, 1991.
Pratt J., H. Raiffa, and R. Schlaifer, Introduction to Statistical Decision Theory, The MIT Press, 1994.
Press S., and J. Tanur, The Subjectivity of Scientists and the Bayesian Approach, Wiley, 2001. Comparing and contrasting the reality of subjectivity in the work of history's great scientists and the modern Bayesian approach to statistical analysis.
Tanaka H., and P. Guo, Possibilistic Data Analysis for Operations Research, Physica-Verlag, 1999.
Decision Analysis: Making Justifiable, Defensible Decisions
Decision analysis is the discipline of evaluating complex alternatives in terms of values and uncertainty. Values are generally expressed monetarily because this is a major concern for management. Furthermore, decision analysis provides insight into how the defined alternatives differ from one another and then generates suggestions for new and improved alternatives. Numbers quantify subjective values and uncertainties, which enable us to understand the decision situation. These numerical results then must be translated back into words in order to generate qualitative insight.Humans can understand, compare, and manipulate numbers. Therefore, in order to create a decision analysis model, it is necessary to create the model structure and assign probabilities and values to fill the model for computation. This includes the values for probabilities, the value functions for evaluating alternatives, the value weights for measuring the trade-off objectives, and the risk preference.
Once the structure and numbers are in place, the analysis can begin. Decision analysis involves much more than computing the expected utility of each alternative. If we stopped there, decision makers would not gain much insight. We have to examine the sensitivity of the outcomes, weighted utility for key probabilities, and the weight and risk preference parameters. As part of the sensitivity analysis, we can calculate the value of perfect information for uncertainties that have been carefully modeled.
There are two additional quantitative comparisons. The first is the direct comparison of the weighted utility for two alternatives on all of the objectives. The second is the comparison of all of the alternatives on any two selected objectives which shows the Pareto optimality for those two objectives.
Complexity in the modern world, along with information quantity, uncertainty, and risk, make it necessary to provide a rational decision making framework. The goal of decision analysis is to give guidance, information, insight, and structure to the decision-making process in order to make better, more 'rational' decisions.

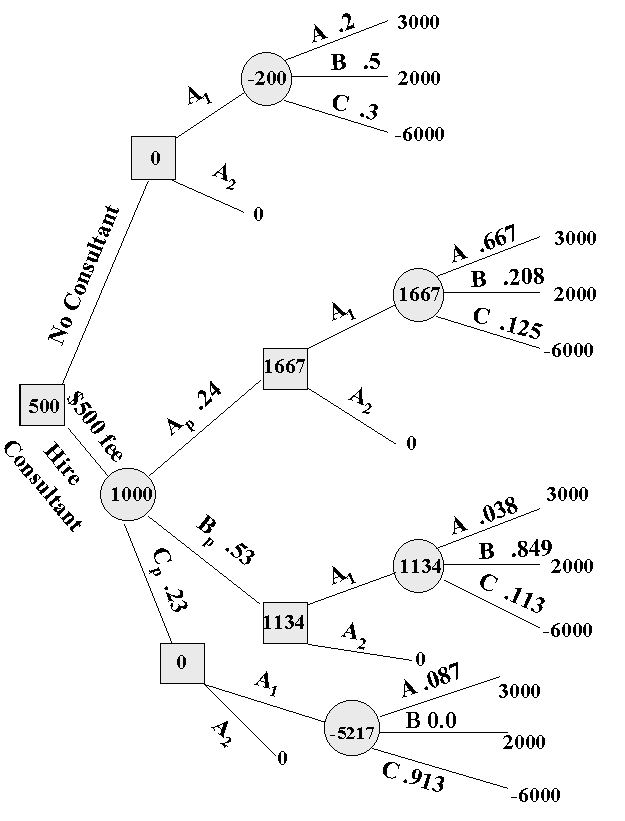
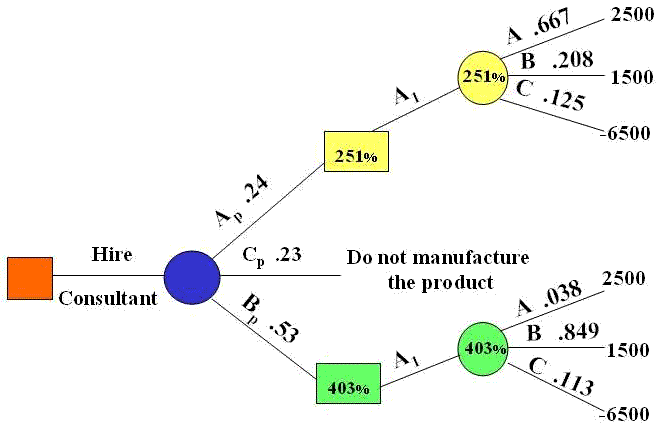
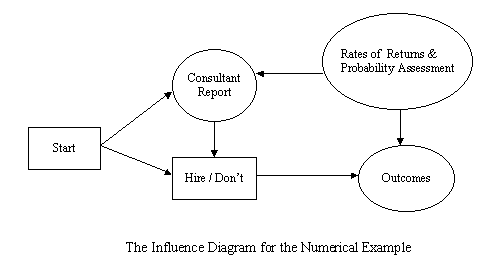
A decision needs a decision maker who is responsible for making decisions. This decision maker has a number of alternatives and must choose one of them. The objective of the decision-maker is to choose the best alternative. When this decision has been made, events that the decision-maker has no control over may have occurred. Each combination of alternatives, followed by an event happening, leads to an outcome with some measurable value. Managers make decisions in complex situations. Decision tree and payoff matrices illustrate these situations and add structure to the decision problems.
Further Readings:
Arsham H., Decision analysis: Making justifiable, defensible decisions,
e-Quality, September, 2004.
Forman E., and M. Selly, Decision by Objectives: How to Convince Others That You Are Right, World Scientific, 2001.
Gigerenzer G., Adaptive Thinking: Rationality in the Real World, Oxford University Press, 2000.
Girón F., (Ed.), Applied Decision Analysis, Kluwer Academic, 1998.
Manning N., et al., Strategic Decision Making In Cabinet Government: Institutional Underpinnings and Obstacles, World Bank, 1999.
Patz A., Strategic Decision Analysis: A General Management Framework, Little and Brown Pub., 1981.
Vickers G., The Art of Judgment: A Study of Policy Making, Sage Publications, 1995.
Von Furstenberg G., Acting Under Uncertainty: Multidisciplinary Conceptions, Kluwer Academic Publishers, 1990.
Elements of Decision Analysis Models
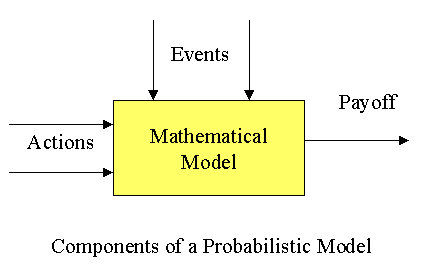
The mathematical models and techniques considered in decision analysis are concerned with prescriptive theories of choice (action). This answers the question of exactly how a decision maker should behave when faced with a choice between those actions which have outcomes governed by chance, or the actions of competitors.
Decision analysis is a process that allows the decision maker to select at least and at most one option from a set of possible decision alternatives. There must be uncertainty regarding the future along with the objective of optimizing the resulting payoff (return) in terms of some numerical decision criterion.
The elements of decision analysis problems are as follow:
- A sole individual is designated as the decision-maker. For example, the CEO of a company, who is accountable to the shareholders.
- A finite number of possible (future) events called the 'States of Nature' (a set of possible scenarios). They are the circumstances under which a decision is made. The states of nature are identified and grouped in set "S"; its members are denoted by "s(j)". Set S is a collection of mutually exclusive events meaning that only one state of nature will occur.
- A finite number of possible decision alternatives (i.e., actions) is available to the decision-maker. Only one action may be taken. What can I do? A good decision requires seeking a better set of alternatives than those that are initially presented or traditionally accepted. Be brief on the logic and reason portion of your decision. While there are probably a thousand facts about an automobile, you do not need them all to make a decision. About a half dozen will do.
- Payoff is the return of a decision. Different combinations of decisions and states of nature (uncertainty) generate different payoffs. Payoffs are usually shown in tables. In decision analysis payoff is represented by positive (+) value for net revenue, income, or profit and negative (-) value for expense, cost or net loss. Payoff table analysis determines the decision alternatives using different criteria. Rows and columns are assigned possible decision alternatives and possible states of nature, respectively.
Constructing such a matrix is usually not an easy task; therefore, it may take some practice.
Source of Errors in Decision Making: The main sources of errors in risky decision-making problems are: false assumptions, not having an accurate estimation of the probabilities, relying on expectations, difficulties in measuring the utility function, and forecast errors.
Consider the following Investment Decision-Making Example:
The Investment Decision-Making Example:
| States of Nature | |||||
| Growth | Medium G | No Change | Low | ||
| G | MG | NC | L | ||
| Bonds | 12% | 8 | 7 | 3 | |
| Actions | Stocks | 15 | 9 | 5 | -2 |
| Deposit | 7 | 7 | 7 | 7 | |
The States of Nature are the states of economy during one year. The problem is to decide what action to take among three possible courses of action with the given rates of return as shown in the body of the table.
Further Readings:
Borden T., and W. Banta, (Ed.), Using Performance Indicators to Guide Strategic Decision Making, Jossey-Bass Pub., 1994.
Eilon S., The Art of Reckoning: Analysis of Performance Criteria, Academic Press, 1984.
Von Furstenberg G., Acting Under Uncertainty: Multidisciplinary Conceptions, Kluwer Academic Publishers, 1990.
Coping With Uncertainties
There are a few satisfactory description of uncertainty, one of which is the concept and the algebra of probability.
To make serious business decisions one is to face a future in which ignorance and uncertainty increasingly overpower knowledge, as ones planning horizon recedes into the distance. The deficiencies about our knowledge of the future may be divided into three domains, each with rather murky boundaries:
- Risk: One might be able to enumerate the outcomes and figure the probabilities. However, one must lookout for non-normal distributions, especially those with fat tails, as illustrated in the stock market by the rare events.
- Uncertainty: One might be able to enumerate the outcomes but the probabilities are murky. Most of the time, the best one can do is to give a rank order to possible outcomes and then be careful that one has not omitted one of significance.
- Black Swans: The name comes from an Australian genetic anomaly. This is the domain of events which are either extremely unlikely or inconceivable but when they happen, and they do happen, they have serious consequences, usually bad. An example of the first kind is the Exxon Valdez oil spill, of the second, the radiation accident at Three Mile Island.
In fact, all highly man-made systems, such as, large communications networks, nuclear-powered electric-generating stations and spacecraft are full of hidden paths to failure, so numerous that we cannot think of all of them, or not able to afford the time and money required to test for and eliminate them. Individually each of these paths is a black swan, but there are so many of them that the probability of one of them being activated is quite significant.
Continuum of pure uncertainty and certainty: The domain of decision analysis models falls between two extreme cases. This depends upon the degree of knowledge we have about the outcome of our actions, as shown below:
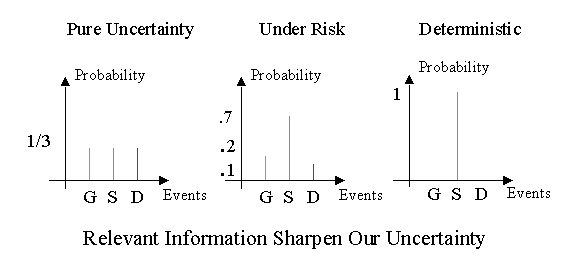
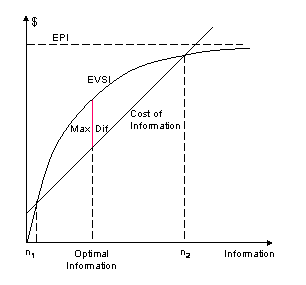
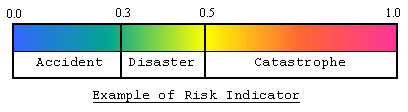
 provided
provided