Introduction
The main idea of statistical inference is to take a random sample from a population and then to use the information from the sample to make inferences about particular population characteristics such as the mean (measure of central tendency), the standard deviation (measure of spread) or the proportion of units in the population that have a certain characteristic. Sampling saves money, time, and effort. Additionally, a sample can, in some cases, provide as much information as a corresponding study that would attempt to investigate an entire population-careful collection of data from a sample will often provide better information than a less careful study that tries to look at everything.We must study the behavior of the mean of sample values from different specified populations. Because a sample examines only part of a population, the sample mean will not exactly equal the corresponding mean of the population. Thus, an important consideration for those planning and interpreting sampling results, is the degree to which sample estimates, such as the sample mean, will agree with the corresponding population characteristic.
In practice, only one sample is usually taken (in some cases such as "survey data analysis" a small "pilot sample" is used to test the data-gathering mechanisms and to get preliminary information for planning the main sampling scheme). However, for purposes of understanding the degree to which sample means will agree with the corresponding population mean, it is useful to consider what would happen if 10, or 50, or 100 separate sampling studies, of the same type, were conducted. How consistent would the results be across these different studies? If we could see that the results from each of the samples would be nearly the same (and nearly correct!), then we would have confidence in the single sample that will actually be used. On the other hand, seeing that answers from the repeated samples were too variable for the needed accuracy would suggest that a different sampling plan (perhaps with a larger sample size) should be used.
A sampling distribution is used to describe the distribution of outcomes that one would observe from replication of a particular sampling plan.
Know that estimates computed from one sample will be different from estimates that would be computed from another sample.
Understand that estimates are expected to differ from the population characteristics (parameters) that we are trying to estimate, but that the properties of sampling distributions allow us to quantify, probabilistically, how they will differ.
Understand that different statistics have different sampling distributions with distribution shapes depending on (a) the specific statistic, (b) the sample size, and (c) the parent distribution.
Understand the relationship between sample size and the distribution of sample estimates.
Understand that the variability in a sampling distribution can be reduced by increasing the sample size.
See that in large samples, many sampling distributions can be approximated with a normal distribution.
Variance and Standard Deviation
Deviations about the mean of a population is the basis for most of the statistical tests we will learn. Since we are measuring how widely a set of scores is dispersed about the mean we are measuring variability. We can calculate the deviations about the mean, and express it as variance or standard deviation. It is very important to have a firm grasp of this concept because it will be a central concept throughout the course.Both variance and standard deviation measures variability within a distribution. Standard deviation is a number that indicates how much, on average, each of the values in the distribution deviates from the mean (or center) of the distribution. Keep in mind that variance measures the same thing as standard deviation (dispersion of scores in a distribution). Variance, however, is the average squared deviations about the mean. Thus, variance is the square of the standard deviation.
In terms of quality of goods/services, It is important to know that higher variation means lower quality. Measuring the size of variation and its source is the statistician's job, while fixing it is the job of the engineer or the manager. Quality products and services have low variation.
What Is a Confidence Interval?
In practice, a confidence interval is used to express the uncertainty in a quantity being estimated. There is uncertainty because inferences are based on a random sample of finite size from a population or process of interest. To judge the statistical procedure we can ask what would happen if we were to repeat the same study, over and over, getting different data (and thus different confidence intervals) each time.Know that a confidence interval computed from one sample will be different from a confidence interval computed from another sample.
Understand the relationship between sample size and width of confidence interval.
Know that sometimes the computed confidence interval does not contain the true mean value (that is, it is incorrect) and understand how this coverage rate is related to confidence level.
Questionnaire Design and Surveys Management
When the sampling units are human beings, the main methods of collecting information are:
- face-to-face interviewing
postal surveys
- telephone surveys
- direct observation.
- Internet
The main questions are:
What is the purpose of the survey?
What kinds of questions the survey would be developed to answer?
What sorts of actions is the company considering based on the results of the survey?
Step 1: Planning Questionnaire Research
Consider the advantages and disadvantages of using questionnaires.
Prepare written objectives for the research.
Have your objectives reviewed by others.
Review the literature related to the objectives.
Determine the feasibility of administering your questionnaire to the population of interest.
Prepare a time-line.
Step 2. Conducting Item Try-Outs and an Item Analysis
Have your items reviewed by others.
Conduct "think-aloud" with several people.
Carefully select individuals for think-aloud.
Consider asking about 10 individuals to write detailed responses on a draft of your questionnaire.
Ask some respondents to respond to the questionnaire for an item analysis. In the first stage of an item analysis, tally the number of respondents who selected each choice.
In the second stage of an item analysis, compare the responses of high and low groups on individual items.
Step 3: Preparing a Questionnaire for Administration
Write a descriptive title for the questionnaire.
Write an introduction to the questionnaire.
Group the items by content, and provide a subtitle for each group.
Within each group of items, place items with the same format
together.
At the end of the questionnaire, indicate what respondents should do next.
Prepare an informed consent form, if needed.
If the questionnaire will be mailed to respondents, avoid having your correspondence look like junk mail.
If the questionnaire will be mailed, consider including a token reward.
If the questionnaire will be mailed, write a follow-up letter.
If the questionnaire will be administered in person, consider preparing written instructions for the administrator.
Step 4: Selecting a Sample of Respondents
Identify the accessible population.
Avoid using samples of convenience.
Simple random sampling is a desirable method of sampling.
Systematic sampling is an acceptable method of sampling.
Stratification may reduce sampling errors.
Consider using random cluster sampling when every member of a population belongs to a group.
Consider using multistage sampling to select respondents from large populations.
Consider the importance of getting precise results when determining sample size.
Remember that using a large sample does not compensate for a bias in sampling.
Consider sampling non respondents to get information on the nature of a bias.
The bias in the mean is the difference of the population means for respondents and non respondents multiplied by the population nonresponse rate.
Step 5: Preparing Statistical Tables and Figures
Prepare a table of frequencies.
Consider calculating percentages and arranging them in a table with the frequencies.
For nominal data, consider constructing a bar graph.
Consider preparing a histogram to display a distribution of scores.
Consider preparing polygons if distributions of scores are to be compared.
Step 6: Describing Averages and Variability
Use the median as the average for ordinal data.
Consider using the mean as the average for equal interval data.
Use the median as the average for highly skewed, equal interval data.
Use the range very sparingly as the measure of variability.
If the median has been selected as the average, use the interquartile range as the measure of variability.
If the mean has been selected as the average, use the standard deviation as the measure of variability.
Keep in mind that the standard deviation has a special relationship to the normal curve that helps in its interpretation.
For moderately asymmetrical distributions the mode, median and mean satisfy the formula: mode=3*median-2*mean.
Step 7: Describing Relationships
For the relationship between two nominal variables, prepare a contingency table.
When groups have unequal numbers of respondents, include percentages in contingency tables.
For the relationship between two equal interval variables, compute a correlation coefficient.
Interpret a Pearson r using the coefficient of determination.
For the relationship between a nominal variable and an equal interval variable, examine differences among averages.
Step 8: Estimating Margins of Error
It is extremely difficult, and often impossible, to evaluate the effects of a bias in sampling.
When evaluating a percentage, consider the standard error of a percentage.
When evaluating a mean, consider the standard error of the mean.
When evaluating a median, consider the standard error of the median.
Consider building confidence intervals, especially when comparing two or more groups
Step 9: Writing Reports of Questionnaire Research
In an informal report, variations in the organization of the report are permitted.
Academic reports should begin with a formal introduction that cites literature.
The second section of academic reports should describe the research methods.
The third section of academic reports should describe the results.
The last section of academic reports should be a discussion. Acknowledge any weakness in your research methodology.
Missing Values on a Sensitive Topic
A natural way to get answers is to, as much as possible, assure people that the surveys are anonymous, and to find a way to make the respondent at least minimally comfortable. So, according to US General Accounting Office book, "Developing and Using Questionnaires" (Oct 1983) chapter 9, you should do the following:
- explain to respondent the reasons for asking the questions,
- make response categories as broad as possible.
- word the question in a nonjudgemental style that avoids the appearance of censure, or, if possible, make the behavior in question appear to be socially acceptable.
- present the request as factual matter as possible.
- guarantee confidentiality or anonymity
- make sure the respondent knows the info will not be used in any threatening way.
- explain how the info will be handled
- avoid cross classification that will allow for pinpointing responses.
Source of Errors
- The use of an inadequate frame.
- A poorly designed questionnaire.
- Recording and measurement errors.
- Non-response problems.
For example consider the following question: "Over the last twelve months would you say your health has on the whole been : Good? / Fairly good? / Not good?" . The respondent is required to tick one of 3 thus-labeled boxes.
What is wrong with the following:
It is the ONLY question on the form, which asks about a matter of opinion rather than fact, but this distinction is not in any way represented in its layout or wording.
Whereas for a question about opinion there should be a response option of 'Don't Know' this is not provided. In some cases, such as the Census Form and the Census advisory staff are adamant that the question must be answered. Thus a person with no opinion on the matter is in a quandary and threatened with possible legal action.
This particular question is highly ambiguous as regards the qualitative nature of what is being asked about (your health). Is one to respond in terms of how one feels, how one can perform, comparisons with peer groups, comparisons with other periods of one's life, or what?
Relatively recent innovations surrounding the Internet have spawned new ways for conducting surveys: most notably electronic mail (e-mail) surveys and WWW surveys. While still in its infancy, it is clear that the Internet is here to stay and this new medium is going to be used for survey data collection. The main question is how the Internet can be used for survey data collection by some effective and efficient design considerations.
Survey Non-Sampling Errors: The widely used measure of the total error in a survey estimated is the mean squared error (MSE). The MSE consists of two components: variance and the square of the bias. Survey researchers are able to obtain a good quantitative estimated of the variance component of mean squared error. Unfortunately, the theory and methods of estimating the bias (non-sampling error) component are underdeveloped. Because the non-sampling error is usually much greater than the sampling error in estimates from large sample surveys, it is imperative that we learn more about it. In recent years U.S. Bureau of Labor Statistics measures various aspects of non-sampling error by means of behavioral science among others.
Further Reading:
Biemer P., and L.Lyberg, Introduction to Survey Quality, Wiley, 2003.
Lehtonen R., and E. Pahkinen, Practical Methods for Design and Analysis of Complex Surveys, Wiley, 2003.
General Sampling Techniques
From the food you eat to the TV you watch, from political elections to school board actions, much of your life is regulated by the results of sample surveys. In the information age of today and tomorrow, it is increasingly important that sample survey design and analysis be understood by many so as to produce good data for decision making and to recognize questionable data when it arises. Relevant topics are: Simple Random Sampling, Stratified Random Sampling, Cluster Sampling, Systematic Sampling, Ratio and Regression Estimation, Estimating a Population Size, Sampling a Continuum of Time, Area or Volume, Questionnaire Design, Errors in Surveys.A sample is a group of units selected from a larger group (the population). By studying the sample it is hoped to draw valid conclusions about the larger group.
A sample is generally selected for study because the population is too large to study in its entirety. The sample should be representative of the general population. This is often best achieved by random sampling. Also, before collecting the sample, it is important that the researcher carefully and completely defines the population, including a description of the members to be included.
Random Sampling: Random sampling of size n from a population size N. Unbiased estimate for variance of 
is Var() = S2(1-n/N)/n, where n/N is the sampling fraction. For sampling fraction less than 10% the finite population correction factor (N-n)/(N-1) is almost 1.
The total T is estimated by N. , its variance is N2Var().
For 0, 1, (binary) type variables, variation in estimated proportion p is:
For ratio r = Sxi/Syi=
/ 
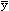, the variation for r is
2].Stratified Sampling: Stratified sampling can be used whenever the population can be partitioned into smaller sub-populations, each of, which is homogeneous according to the particular characteristic of interest.
s = S Wt. Bxart, over t=1, 2, ..L (strata), and t is SXit/nt.
Its variance is:
Population total T is estimated by N. s, its variance is
Since the survey usually measures several attributes for each population member, it is impossible to find an allocation that is simultaneously optimal for each of those variables. Therefore, in such a case we use the popular method of allocation which use the same sampling fraction in each stratum. This yield optimal allocation given the variation of the strata are all the same.
Determination of sample sizes (n) with regard to binary data: Smallest integer greater than or equal to:
[t2 N p(1-p)] / [t2 p(1-p) + a2 (N-1)]
with N being the size of the total number of cases, n being the sample size, a the expected error, t being the value taken from the t distribution corresponding to a certain confidence interval, and p being the probability of an event.
Cross-Sectional Sampling: Cross-Sectional Study the observation of a defined population at a single point in time or time interval. Exposure and outcome are determined simultaneously.
Quota Sampling: Quota sampling is availability sampling, but with the constraint that proportionality by strata be preserved. Thus the interviewer will be told to interview so many white male smokers, so many black female nonsmokers, and so on, to improve the representatives of the sample. Maximum variation sampling is a variant of quota sampling, in which the researcher purposively and non-randomly tries to select a set of cases, which exhibit maximal differences on variables of interest. Further variations include extreme or deviant case sampling or typical case sampling.
What is a statistical instrument? A statistical instrument is any process that aim at describing a phenomena by using any instrument or device, however the results may be used as a control tool. Examples of statistical instruments are questionnaire and surveys sampling.
What is grab sampling technique? The grab sampling technique is to take a relatively small sample over a very short period of time, the result obtained are usually instantaneous. However, the Passive Sampling is a technique where a sampling device is used for an extended time under similar conditions. Depending on the desirable statistical investigation, the Passive Sampling may be a useful alternative or even more appropriate than grab sampling. However, a passive sampling technique needs to be developed and tested in the field.
Further Reading:
Thompson S., Sampling, Wiley, 2002.
What Is the Margin of Error
Estimation is the process by which sample data are used to indicate the value of an unknown quantity in a population.Results of estimation can be expressed as a single value; known as a point estimate, or a range of values, referred to as a confidence interval.
Whenever we use point estimation, we calculate the margin of error associated with that point estimation. For example; for the estimation of the population proportion, by the means of sample proportion (P), the margin of errors calculated often as follows:
In newspapers and television reports on public opinion pools, the margin of error is often appears in small font at the bottom of a table or screen, respectively. However, reporting the amount of error only, is not informative enough by itself, what is missing is the degree of the confidence in the findings. The more important missing piece of information is the sample size n. that is, how many people participated in the survey, 100 or 100000? By now, you know it well that the larger the sample size the more accurate is the finding, right?
The reported margin of error is the margin of "sampling error". There are many nonsampling errors that can and do affect the accuracy of polls. Here we talk about sampling error. The fact that subgroups have larger sampling error than one must include the following statement: "Other sources of error include but are not limited to, individuals refusing to participate in the interview and inability to connect with the selected number. Every feasible effort is made to obtain a response and reduce the error, but the reader (or the viewer) should be aware that some error is inherent in all research."
If you have a yes/no question in a survey, you probably want to calculate a proportion P of Yes's (or No's). Under simple random sampling survey, the variance of P is P(1-P)/n, ignoring the finite population correction, for large n, say over 30. Now a 95% confidence interval is
References and Further Readings:
Casella G., and R. Berger, Statistical Inference, Wadsworth Pub. Co., 2001.
Kish L., Survey Sampling, Wiley, 1995.
Lehmann E., and G. Casella, Theory of Point Estimation, Springer Verlag, New York, 1998.
Levy P., and S. Lemeshow, Sampling of Populations: Methods and Applications, Wiley, 1999.
Sample Size Determination
The question of how large a sample to take arises early in the planning of any survey. This is an important question that should be treated lightly. To take a large sample than is needed to achieve the desired results is wasteful of resources whereas very small samples often lead to that are no practical use of making good decision. The main objective is to obtain both a desirable accuracy and a desirable confidence level with minimum cost.Pilot Sample: A pilot or preliminary sample must be drawn from the population and the statistics computed from this sample are used in determination of the sample size. Observations used in the pilot sample may be counted as part of the final sample, so that the computed sample size minus the pilot sample size is the number of observations needed to satisfy the total sample size requirement.
People sometimes ask me, what fraction of the population do you need? I answer, "It's irrelevant; accuracy is determined by sample size alone" This answer has to be modified if the sample is a sizable fraction of the population.
For an item scored 0/1 for no/yes, the standard deviation of the item scores is given by SD = [p(1-p)/N] 1/2 where p is the proportion obtaining a score of 1, and N is the sample size.
The standard error of estimate SE (the standard deviation of the range of possible p values based on the pilot sample estimate) is given by SE= SD/N½. Thus, SE is at a maximum when p = 0.5. Thus the worst case scenario occurs when 50% agree, 50% disagree.
The sample size, N, can then be expressed as largest integer less than or equal to 0.25/SE2
Thus, for SE to be 0.01 (i.e. 1%), a sample size of 2500 would be needed; 2%, 625; 3%, 278; 4%, 156, 5%, 100.
Note, incidentally, that as long as the sample is a small fraction of the total population, the actual size of the population is entirely irrelevant for the purposes of this calculation.
Sample sizes with regard to binary data:
with N being the size of the total number of cases, n being the sample size, a the expected error, t being the value taken from the t distribution corresponding to a certain confidence interval, and p being the probability of an event.
For a finite population of size N, the standard error of the sample mean of size n, is:
There are several formulas for the sample size needed for a t-test. The simplest one is
The simplest approximation is to replace the first Z value in the above formula with the value from the studentized range statistic that is used to derive Tukey's follow-up test. If you don't have sufficiently detailed tables of the studentized range, you can approximate the Tukey follow-up test using a Bonferroni correction. That is, change the first Z value to Za where k is the number of comparisons.
Neither of these solutions is exact and the exact solution is a bit messy. But either of the above approaches is probably close enough, especially if the resulting sample size is larger than (say) 30.
A better stopping rule for conventional statistical tests is as
follows:
Test some minimum (pre-determined) number of subjects.
Stop if p-value is equal to or less than .01, or p-value equal to or greater than .36; otherwise, run more subjects.
Obviously, another option is to stop if/when the number of subjects becomes too great for the effect to be of practical interest. This procedure maintains a about 0.05.
We may categorized probability proportion to size (PPS) sampling, stratification, and ratio estimation (or any other form of model assisted estimation) as tools that protect one from the results of a very unlucky sample. The first two (PPS sampling and stratification) do this by manipulation of the sampling plan (with PPS sampling conceptually a limiting case of stratification). Model assisted estimation methods such as ratio estimation serve the same purpose by introduction of ancillary information into the estimation procedure. Which tools are preferable depends, as others have said, on costs, availability of information that allows use of these tools, and the potential payoffs (none of these will help much if the stratification/PPS/ratio estimation variable is not well correlated with the response variable of interest).
There are also heuristic methods for determination of sample size. For example, in healthcare behavior and process measurement sampling criteria are designed for a 95% CI of 10 percentage points around a population mean of 0.50; There is a heuristic rule: "If the number of individuals in the target population is smaller than 50 per month, systems do not use sampling procedures but, attempt to collect data from all individuals in the target population."
Further Readings:
Goldstein H., Multilevel Statistical Models, Halstead Press, 1995.
Kish R., G. Kalton, S. Heeringa, C. O'Muircheartaigh, and J. Lepkowski, Collected Papers of Leslie Kish, Wiley, 2002.
Kish L., Survey Sampling, Wiley, 1995.
Percentage: Estimation and Testing
The following are two JavaScript applets that construct exact confidence intervals and test of hypothesis with respect to proportion, percentage, and binomial distribution with or without a finite population, respectively.Enter the needed information, and then click the Calculate button.
Application to the test of hypothesis: Notice that, one may utilize Confidence Interval (CI) for the test of hypothesis purposes. Suppose you wish to test the following general test of hypothesis:
H0: The population parameter is almost equal to a given claimed value,
against the alternative:
Ha: The population parameter is not even close to the claimed value.
The process of carrying the above test of hypothesis at a level of significance using CI is as follow:
- Ignore the claimed value in the null hypothesis, for time being.
- Construct a 100(1- a)% confidence interval based on the available data.
- If the constructed CI does not contain the claimed value, then there is enough evidence to reject the null hypothesis. Otherwise, there is no reason to reject the null hypothesis.
Sample Size with Acceptable Absolute Precision: The followings present the widely used method for determining the sample size required for estimating a population mean or proportion.
Let us suppose we want an interval that extends d unit on either side of the estimator. We can write
d = Absolute Precision = (reliability coefficient) .(standard error) = Z a/2 . (S/n1/2)
You may like using Sample Size Determination Applet to check your computations.
Multilevel Statistical Models
Many kinds of data, including observational data collected in the human and biological sciences, have a hierarchical or clustered structure. For example, animal and human studies of inheritance deal with a natural hierarchy where offspring are grouped within families. Offspring from the same parents tend to be more alike in their physical and mental characteristics than individuals chosen at random from the population at large.Many designed experiments also create data hierarchies, for example clinical trials carried out in several randomly chosen centers or groups of individuals. Multilevel models are concerned only with the fact of such hierarchies not their provenance. We refer to a hierarchy as consisting of units grouped at different levels. Thus offspring may be the level 1 units in a 2-level structure where the level 2 units are the families: students may be the level 1 units clustered within schools that are the level 2 units.
The existence of such data hierarchies is not accidental and should not be ignored. Individual people differ as do individual animals and this necessary differentiation is mirrored in all kinds of social activity where the latter is often a direct result of the former, for example when students with similar motivations or aptitudes are grouped in highly selective schools or colleges. In other cases, the groupings may arise for reasons less strongly associated with the characteristics of individuals, such as the allocation of young children to elementary schools, or the allocation of patients to different clinics. Once groupings are established, even if their establishment is effectively random, they will tend to become differentiated, and this differentiation implies that the group' and its members both influence and are influenced by the group membership. To ignore this relationship risks overlooking the importance of group effects, and may also render invalid many of the traditional statistical analysis techniques used for studying data relationships.
A simple example will show its importance. A well known and influential study of primary (elementary) school children carried out in the 1970's claimed that children exposed to so called 'formal' styles of teaching reading exhibited more progress than those who were not. The data were analyzed using traditional multiple regression techniques, which recognized only the individual children as the units of analysis and ignored their groupings within teachers and into classes. The results were statistically significant. Subsequently, it has been demonstrated that when the analysis accounted properly for the grouping of children into classes, the significant differences disappeared and the 'formally' taught children could not be shown to differ from the others.
This re-analysis is the first important example of a multilevel analysis of social science data. In essence what was occurring here was that the children within any one classroom, because they were taught together, tended to be similar in their performance. As a result they provide rather less information than would have been the case if the same number of students had been taught separately by different teachers. In other words, the basic unit for purposes of comparison should have been the teacher not the student. The function of the students can be seen as providing, for each teacher, an estimate of that teacher's effectiveness. Increasing the number of students per teacher would increase the precision of those estimates but not change the number of teachers being compared. Beyond a certain point, simply increasing the numbers of students in this way hardly improves things at all. On the other hand, increasing the number of teachers to be compared, with the same or somewhat smaller number of students per teacher, considerably improves the precision of the comparisons.
Researchers have long recognized this issue. In education, for example, there has been much debate about the so called 'unit of analysis' problem, which is the one just outlined. Before multilevel modelling became well developed as a research tool, the problems of ignoring hierarchical structures were reasonably well understood, but they were difficult to solve because powerful general purpose tools were unavailable. Special purpose software, for example for the analysis of genetic data, has been available longer but this was restricted to 'variance components' models and was not suitable for handling general linear models. Sample survey workers have recognized this issue in another form. When population surveys are carried out, the sample design typically mirrors the hierarchical population structure, in terms of geography and household membership. Elaborate procedures have been developed to take such structures into account when carrying out statistical analyses.
Further Readings:
Goldstein H., Multilevel Statistical Models, Halstead Press, New York, 1995.
Longford N., Random Coefficient Models, Clarendon Press, Oxford, 1993.
These books cover a very wide range of applications and theory.
Surveys Sampling Routines
Note: The following programs are referred to the Practical Methods for Design and Analysis of Complex Surveys, by R. Lehtonen, and E. Pahkinen, Wiley, Chichester, 1995. See also, L.Lyberg et al., (Editors), Survey Measurement and Process Quality, New York, Wiley, 1997.Other software packages such as Le Sphinx, CENVAR, CLUSTERS, Epi Info, Generalized Estimation System, Super CARP, Stata, SUDAAN, VPLX, WesVarPC, and ORIRIS IV.
TITLE Bernoulli sampling; PI=0.25, N=32 GET FILE (input dataset) COMPUTE PI=0.25 COMPUTE EPSN=UNIF(1) SELECT IF (EPSN LT PI) WRITE OUTPUT=(output dataset)TITLE Simple random sampling with replacement; n=8, N=32 GET FILE (input dataset) COMPUTE L=L+ID LEAVE L COMPUTE E=L-ID NUMERIC W(f2) COMPUTE W=0 DO REPEAT A=A1-A8 IF (ID=1) A=UNIF(32) LEAVE A IF (E LT A AND A LE L) W=W + 1 END REPEAT SELECT IF (W GT 0) WRITE OUTFILE = (output dataset)
TITLE Simple random sampling without replacement; n=8, N=32
GET FILE (input dataset) SAMPLE 8 FROM 32 WRITE OUTFILE = (output dataset)TITLE Systematic sampling; n=8, sampling interval =4 MATRIX COMPUTE RAND = TRANC (4*UNIFORM(1,1)) COMPUTE INT=RAND*MAKE(32, 1, 1) SAVE INT/OUTPUT=*/VAR=INT END MATRIX MATCH FILES FILE = (input dataset)/FILE=* COMPUTE INDEX = MOD ($CASENUM, 4) SELECT IF (INDEX=INT) SAVE OUTPUTFILE = (output dataset)/DROP=INDEX INT
The Following routines are for sampling
(selection with probability proportion to size)TITLE PPS Poisson sampling with expected size of 8
GET FILE )input dataset) COMPUTE PI=8*HOU*%/91753 COMPUTE EPSN=UNIF(1) SELECT IF (EPSN LE PI) WRITE OUTFILE (output dataset)TITLE PPS Sampling with replacement; n=8 GET FILE (input dataset) COMPUT L=L+HOU85 LEAVE L COMPUTE E=L-HOU85 NUMERIC W(F2) COMPUTE W=0 DO REPEAT A A1 TO A8 IF (ID=1) A=INIF(91753) LEAVE A IF (E LT A AND ALE L) W=W+1 END REPEAT SELECT IF W GT 0 WRITE OUTFILE = (output dataset)
TITLE PPS Systematic sampling n=8 GET FILE (input dataset) COMPUTE #C=#C + 1 COMPUTE CASE = #C COMPUTE #SN=8 COMPUTE #PN=01753 COMPUTE #INT=TRUNC (#PN/#SN) COMPUTE #RAN= TRUNC (UNIFORM (#INT) +1) DO IF CASE = 1 COMPUTE #COMP=#RAN COMPUTE RAN=#RAN END IF COMPUTE SAMIND=0 LOOP IF +COMP LE CUMHOU*% + COMPUTE SAMIND = SAMIND+1 + COMPUTE #COMP+#COMP+#INT END LOOP EXECUTE. WRITE OUTFILE= (output dataset)
Further Readings:
Bethel J., Sample allocation in multivariate surveys, Survey Methodology, 15, 1989, 47-57.
Valliant R., and J. Gentle, An application of mathematical programming to a sample allocation problem, Computational Statistics and Data Analysis, 25, 1997, 337-360.
Cronbach's Alpha (Coefficient a)
Perhaps the best way to conceptualize Cronbach's Alpha is to think of it as the average of all possible split half reliabilities for a set of items. A split half reliability is simply the reliability between two parts of a test or instrument where those two parts are halves of the total instrument. In general, the reliabilities of these two halves should then be stepped up (Spearman Brown Prophesy Formula) to estimate the reliability for the full length test rather than the reliability between to half length tests. Assuming, for ease of interpretation, that a test has an even number of items (e.g, 10), then items 1-5 versus 6-10 would be one split, evens versus odds would be another and, in fact, with 10 items chosen 5 at a time, there are 10 chose 5 or 252 possible split halves for this test. If we compute each of these stepped up split half reliabilities and averaged them all, this average would be Cronbach's Alpha. Since some splits will be better than others in terms of creating two more closely parallel halves, and the reliability between parallel halves is probably the most appropriate estimate of an instrument's reliability, Cronbach's alpha is often considered a relatively conservative estimate of the internal consistency of a test.The following is a SAS program for computing coefficient alpha or Cronbach's Alpha. Note that, it is an option in the PROC CORR procedure. In SAS, for a WORK data set called ONE, suppose we want the internal consistency or coefficient alpha or Cronbach's alpha for x1-x10, the syntax is:
PROC CORR DATA=WORK.ONE ALPHA; VAR X1-X10; RUN;
There are at least three important caveats to consider when computing coefficient alpha.
Note 1: How to handle "missing" values. In achievement testing, a missing value or a not reached value is traditionally coded as 0 or wrong. The CORR procedure is SAS DOES NOT treating missing as wrong. It is not difficult to write code to force this to happen, but we must write the code. In the above example we could do so as follows:
DATA WORK.ONE;SET WORK.ONE;
ARRAY X {10} X1-X10; /* DEFINING AN
ARRAY FOR THE 10 ITEMS */
DO I=1 TO 10;
IF X(I) = . THEN X(I) = 0; /* FOR EACH ITEM
X1-X10 CHANGING MISSING VALUES (.) TO 0 */
END;
RUN;
Note 2: The use of the NOMISS option in the CORR procedure. This is related to Note 1 above. Another way to handling missing observations is to use the NOMISS option in the CORR procedure. The syntax is as follows:
PROC CORR DATA=WORK.ONE ALPHA NOMISS; VAR X1-X10;
The effect of this is to remove all items X1-X10 from analysis for any record where a at least one of these items X1-X10 are missing. Obviously, for achievement testing, especially for speeded tests, where most examines might not be expected to complete all items, this would be a problem. The use of the NOMISS option would restrict the analysis to the subset of examines who did complete all items and this quite often would not be the population of interest when wishing to establish an internal consistency reliability estimate.
One common approach to resolving this problem might be to define a number of items that must be attempted for the record to be included. Some health status measures, for example the SF-36, have scoring rules that require that at least 50% of the items must be answered for the scale to be defined. If less than half of the items are attempted, then the scale is not interpreted. If the scale is considered valid, by THEIR definition, then all missing values on that scale are replace by the average of the non-missing items on that scale. The SAS code to implement this scoring algorithm is summarized below under the assumption that the scale is has 10 items.
DATA WORK.ONE;SET WORK.ONE;
ARRAY X {10} X1-X10;
IF NMISS(OF X1-X10) > 5 THEN DO I=1 TO 10;
X(I) = .;
END;
ELSE IF NMISS(OF X1-X10) < = 5 THEN DO I=1 TO 10;
IF X(I) =. THEN X(I) = MEAN(OF X1-X10);
END;
RUN;
Note that replacing all missing values with the average of the non-missing values in the cases where then number of missing values is not greater than half of the total number of items will result in an inflated Cronbach's alpha. A better approach would be to remove from consideration records where fewer than 50% of the records are completed and to leave the remaining records intact, with the missing values still in. In other words, to implement that first IF statement above, but to eliminate the ELSE IF clause and then to run the PROC CORR without the NOMISS option. The bottom line: The NOMISS option in PROC CORR in general, and with the ALPHA options in particular must be considered carefully.
Note 3: Making sure that all items in the set are coded in the same direction. Although 0/1 (wrong/right) coding is rarely a problem with this, for Likert or other scales with more than 2 points on the scale, it is not uncommon for the scale to remain constant (e.g., Strongly Agree, Agree, Disagree, Strongly Disagree), but for the wording of the questions to reverse the appropriate interpretation of the scale. For example,
Q1. Social Security System Must be reformed SA A D SD Q2. Social Security System Remain the Same SA A D SD
Clearly, the two questions are on the same scale, but the meanings of the end points opposite.
In SAS, the way to adjust for this problem is to pick the direction that we want the scale to be coded, that is, do we want SA to be a positive statement about the Social Security System or a negative one, and then reverse scale those items were SA reflects negatively (or positively) about Social Security System. In the above example, SA for Q1 is a negative position relative to the Social Security System and, therefore should be reverse scaled if the decision is to scale so the SA implies positive attitudes.
If the coding of the 4-point Likert Scale was SA-0, A-1, D-2, SD-3, then the item will be reverse scaled as follows:
Q1 = 3-Q1, in this way 0 becomes 3-0 = 1; 1 becomes 3-1 = 2; 2 becomes 3-2 = 1; and 3 becomes 3-3 = 0.
If the coding of the 4-point Likert Scale was SA-1, A-2, D-3, SD-4, then the item will be reverse scaled as follows:
Q1 = 5-Q1, in this way 1 becomes 5-1 = 4; 2 becomes 5-2 = 3; 3 becomes 5-3 = 2; and 4 becomes 5-4 = 1.
From the earlier example, If items X1, X3, X5, X7, and X9 would need to be reverse scaled for before computing an internal consistency estimate, then the following SAS code would do the job, Assuming a the 4-point Likert scale illustrated above with 1-4 scoring.
DATA WORK.ONE;SET WORK.ONE;
ARRAY X {10} X1-X10;
/* DEFINING AN ARRAY FOR THE 10 ITEMS */
DO I=1,3,5,7,9; /* INDICATING WHICH ITEMS
IN THE ARRAY TO BE REVERSE SCALED */
X(I) = 5-X(I); /* REVERSE SCALING
FOR 1-4 CODING OF 4-POINT LIKERT SCALE */
END;
RUN;
It should be noted that some of the output from PROC CORR with the ALPHA option, such as the correlation of the item with the total and the internal consistency estimate for the scale with each individual item NOT part of the scale provides very useful diagnostics that should alert the researcher about either poorly functioning items or items that were missed when considering reverse scaling. An item that correlated negatively with the total usually needs to be reverse scaled or is poorly formed.
Further Readings:
Feldt L., and R. Brennan, Reliability, in Educational Measurement, Linn R. (Ed.), 105-146, 1989, Macmillian Publishing Company.
The Inter-Rater Reliability
The inter-rater reliability between survey interviewers is rarely computed because different interviewers do not usually go back to ask respondents the same questions and groups of respondents interviewed by different interviewers are not always comparable. Especially in personal interview surveys, interviewers may be assigned to different areas of a city or region that differ a great deal compositionally. Survey designers should, however, consider what might give rise to random variation in Interviewers' performance before starting the study arid standardize the training and field procedures to reduce these sources of variation as much as possible.
References and Further Readings:
Aday L., Designing and Conducting Health Surveys: A Comprehensive Guide, Jossey-Bass Publishers, CA, 1996.
Instrumentality Theory
Suppose two corresponding items, one from the dimension being rated and its mate, the relative importance of that topic, called the "valence", are cross-multiplied, then added up across all such pairs, then divided by the number of such pairs. This procedure provides a weighted score, the sum of the items each weighted by its relative importance. The higher the average weighted score, the greater the overall importance and rating of the topic. The technique has been well-liked since two issues are being considered here, how satisfied or prepared or . . . someone is, and how important that topic is to them. The approach has been applied to multivariate issues such as factors affecting leaving an organization, job satisfaction, managerial behavior, etc.
References and Further Readings:
Korn, Graubard, Analysis of Health Surveys, Wiley, 1999.
Value Measurements Survey Instruments:
Rokeach's Value Survey
Research into the relationship between peoples values and their actions as consumers is still in its infancy. However, it is an area that is destined to receive increased attention, for it taps a broad dimension of human behavior that could not be explored effectively before the availability of standardized value instruments.
A popular value instrument that has been employed in consumer behavior studies in the Rokeach Value Survey (RVS). This self-administered value inventory is divided into two parts, with each part measuring different but complementary types of personal values. The first part consists of eighteen terminal value items, which are designed to measure the relative importance of end- states of existence (i.e. personal goals). The second part consists of eighteen instrumental value items, which measure basic approaches and individual might take to reach end-state values. Thus, the firs half of the measurement instrument deals with ends, while the second half considers means.
If the items are not reworded to accommodate the Likert format; instead, respondents are asked to indicate the degree of personal importance each RVS value holds, from "very unimportant" to "very important," and then they're given the standard Likert scale next to each RVS value. Some applications use , for example, a 5-point scale and then features a rank-ordering of the top three RVS values after each list of has already been rated, to use in correcting for end-piling. It is show that in many cases, slightly, but not significantly, lower test-retest reliabilities for the Likert versus rank-ordered procedure.
Since the common reason for preferring to use the RVS in a Likert format is to be able to perform normative statistical tests on the data, it is worthwhile to point out that there are good arguments in favor of using normative statistical tests on RVS data with the scale in its original, rank-ordered format, under some conditions.
Further Readings:
Arsham H., Questionnaire Design and Surveys Sampling, SySurvey: The Online Survey Tool, 2002.
Braithwaite V., Beyond Rokeach's equality-freedom model: Two dimensional values in a one dimensional world, Journal of Social Issues , 50, 67-94, 1994.
Boomsma A., M. Van Duijn, and T. Snijders, (eds.), Essays on Item Response Theory, Springer Verlag, 2000.
Gibbins K., and I. Walker, Multiple interpretations of the Rokeach value survey, Journal of Social Psychology, 133, 797-805, 1993.
Sijtsma K., and I. W. Molenaar, Introduction to Nonparametric Item Response Theory, Sage 2002. Provides an alternative to parametric Item Response Theory is non-parametric (ordinal) Item Response Theory, such as the Mokken Scaling method.
Danger of Wrong Survey Design and the Interpretation of the Results
Consequently many people tend to distrust statistics, and to regard statisticians as naïve and incautious. In fact, statisticians are trained:
- to be extremely careful in selecting information on which to base their calculations.
- to make only such deductions as are strictly logical.
Danger of Biased Sources: One of the chief dangers facing a statistician is that the sources of his/her information may be biased. A statistician must therefore always ask himself such questions as:
- Who says this?
- Why does he say it?
- What does he stand to gain from saying it?
- How does he know?
- Could he be lying?
Danger in Designing a "Bad" Questionnaire: In designing a questionnaire the following points should be observed in its design:
- questions should be simple
- questions should be unambiguous
- the best kinds of question are those which allow a pre-printed answer to be ticked
- the questionnaire should be as short as possible
- questions should be neither irrelevant nor too personal
- Leading questions should not be asked. A "leading question" is one that suggests the answer, e.g. the question “Don’t you agree that all sensible people use XYZ soap?” suggests the answer "yes"
- The questionnaire should be designed so that the questions fall into a logical sequence. This will enable the respondent to understand its purpose, and as a result the quality of his answers may be improved.
The Copyright Statement: The fair use, according to the 1996 Fair Use Guidelines for Educational Multimedia, of materials presented on this Web site is permitted for non-commercial and classroom
purposes only.
This site may be mirrored intact (including these notices), on any server
with public access. All files are available at http://home.ubalt.edu/ntsbarsh/Business-stat for mirroring.
Kindly e-mail me your comments, suggestions, and concerns. Thank you.
This site was launched on 2/18/1994, and its intellectual materials have been thoroughly revised on a yearly basis. The current version is the 9th Edition. All external links are checked once a month.
Back to Dr. Arsham's Home Page
EOF: Ó 1994-2015.