"Matrix" is the Latin word for womb, and it retains that sense in English. It can also mean more generally any place in which something is formed or produced.
In using the JavaScript, replace as many zeros as needed with the entries of the matrix staring at the upper left corner of both matrix A, and B. The computational result will be in matrix C.
An [m by n] matrix A is a rectangular array of real numbers with m rows and n columns. (Rows are horizontal and columns are vertical.) The numbers m and n are the dimensions of A. The numbers in the matrix are called its entries. The entry in row i and column j is called aij or Aij.
Addition and Subtraction of Two Matrices: Sum and Difference of Two Matrices: If A and B have the same dimensions, then their sum, A+B, is obtained by adding corresponding entries. In symbols, (A+B)ij = Aij + Bij. If A and B have the same dimensions, then their difference, A - B, is obtained by subtracting corresponding entries. In symbols, (A-B)ij = Aij - Bij.
Scalar Multiple: If A is a matrix and c is a number (sometimes called a scalar in this context), then the scalar multiple, cA, is obtained by multiplying every entry in A by c. In symbols, (cA)ij = c(Aij).
Transpose of a Matrix: The transpose, AT, of a matrix A is the matrix obtained from A by writing its rows as columns. If A is an [m by n] matrix and B = AT, then B is the [n by m] matrix with bij = aji.
Dividing Two Matrices: There is no such a thing as dividing two matrices.
Multiplication of Two Matrices: If A has dimensions [m by n] and B has dimensions [n by p], then the product AB is defined, and has dimensions [m by p]. The entry (AB)ij is obtained by multiplying row i of A by column j of B, which is done by multiplying corresponding entries together and then adding the results.
The following is a numerical example for multiplication of two matrices A, and B, respectively:
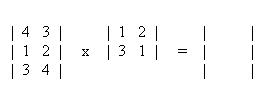
To aid in the multiplication, write the second matrix above and to the right of the first and the resulting matrix at the intersection of the two:
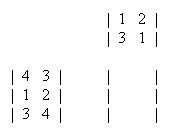
Now, to find the first element of the resulting matrix, C11, take the leftmost number in the corresponding row of the first matrix, 4, multiply it with the topmost number in the corresponding column of the second matrix, 1, and then add the product of the next number to the right in the first matrix and the next number down in the second matrix. For the top left element, it would be the following.
(4)(1) + (3)(3) = 13
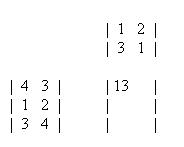
For the top-right element of the resulting matrix, we will still use row 1 of the first matrix but now use column 2 of the second matrix. This element is solved below.
(4)(2) + (3)(1) = 11
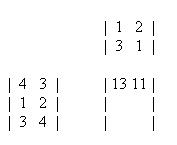
Doing the same with the rest of the numbers leaves the following matrix.
Power of a Matrix: For raising a square matrix A to power of say n = 3, enter the matrix starting at the upper left corner. Then copy it into matrix B by clicking on A ® B, then click on Calculate button, the result is C = A2. Now copy C into B by clicking on C ® B, then click on Calculate button. The result is C = A3.
For larger Value of n there are other possibilities by using your imagination in applying the Copy " ? ® ?" buttons.
Matrix Inversion: The inverse of a square matrix A is a matrix, often denoted by A-1 such that A×A-1 = I, where I is the identity matrix of the same size.
A matrix possessing an inverse is called nonsingular, or invertible.
To invert a matrix, you may like to use the Matrix Inversion JavaScript.