Modelos Dinámicos para Decisiones de Negocios

Toma de Decisiones con Periodos de Tiempo Crítico
en Economía y Finanzas


Sitio Espejo para América Latina


Esta es la versión en Español del sitio Web principal en Inglés, el cual se encuentra disponible en:
Time-Critical Decision Making for Economics and Finance

USA Site

Las herramientas para las decisiones tecnológicas tales como los modelos matemáticos han sido aplicados a una amplia gama de situaciones en la toma de decisiones dentro de diversas áreas de la gerencia. En la toma consciente de decisiones bajo incertidumbre, siempre realizamos pronósticos o predicciones. Podríamos pensar que no estamos pronosticando, pero nuestras opciones estarán dirigidas por la anticipación de resultados de nuestras acciones o inacciones. Este sitio tiene el objetivo de ayudar a los gerentes y administradores a hacer un mejor trabajo al momento de anticipar hechos, y por lo tanto, un mejor manejo de la incertidumbre mediante el uso de técnicas de predicción y pronóstico efectivas.

El uso de modelos matemáticos ha sido incrementado para interpretar y predecir las dinámicas y controles en la toma de decisiones gerenciales. Dichas aplicaciones incluyen pronoacute;stico de ventas, predicciones del impacto y efecto de campañas publicitarias, estrategias para proteger desabastecimiento de inventarios y para determinar estrategias óptimas de inversión de portafolios.

Profesor Hossein Arsham   

Para buscar el sitio, presione Editar| Buscar en la página [Ctrl + f]. Escriba una palabra o frase en el espacio del diálogo. Por ejemplo "método" o "pronóstico" Si el primer resultado de la palabra o la frase no es lo que usted buscaba, intente con Próxima búsqueda.

    CONTENIDO


Capítulo 1:   Implementación de Modelos Cuantitativos

  1. Introducción
  2. Modelos Efectivos para una Buena Toma de Decisiones

Capítulo 2:   Balanceando el Éxito en los Negocios

Capítulo 3:   Modelos para Pronósticos

Capítulo 4:   Series de Tiempo Estacionarias

Capítulo 5:   Modelamiento Causal y de Pronóstico

  1. Modelamiento de Series de Tiempo Causal
  2. Sumario de Métodos de Pronóstico (Introducción)
  3. Como Hacer Pronósticos Mediante Análisis de Regresión
  4. Planificación, Desarrollo y Mantenimiento de un Modelo Lineal
  5. Análisis de Tendencia
  6. Modelando la Estacionalidad y Tendencia
  7. Análisis de Descomposición

Capítulo 6:   Técnicas de Ablandamiento

  1. Promedios Móviles Simples
  2. Promedios Móviles Ponderados
  3. Técnicas de Atenuaciones Exponenciales
  4. Pronoacute;sticos con un Periodo Adelantado

Capítulo 7:   Metodología de la Box-Jenkins

  1. Metodología de la Box-Jenkins
  2. Modelos de Auto Regresión

Capítulo 8:   Técnicas de Filtraje

  1. Filtraje Adaptativo
  2. Filtro de Hodrick-Prescott
  3. Filtro de Kalman

Capítulo 9:   Sumario de Técnicas de Modelos Especiales

  1. Redes Neurales
  2. Modelamiento y Simulación
  3. Modelos Probabilísticos
  4. Números Indices
  5. Análisis de Eventos Históricos
  6. Predicción de la Respuesta de los Mercados
  7. Predicción de Intervalos para Variables Aleatorias
  8. Análisis de Delphi
  9. Metodología de Transferencia de Funciones
  10. Prueba y Estimación de Cambios Estructurales Múltiples
  11. Combinaciones de Pronósticos

Capítulo 10:   Modelos Financieros, Series de Tiempo y Econometría

  1. Modelos Financieros, Series de Tiempo y Econometría
  2. Método del II Censo de Análisis de Estacionalidad
  3. Econometría y Modelos de Serie de Tiempo
  4. Ecuaciones Simultáneas
  5. Medición para Exactitud
  6. Lecturas Adicionales

Capítulo 11:   El Mejor Momento para Reemplazar Equipos

Capítulo 12:   Análisis de Pareto: El ABC para la Clasificación de Inventarios

Capítulo 13:   Análisis de Costo Beneficio: Cantidad Económica

Capítulo 14:   Modelamiento de una Campaña Publicitaria

Capítulo 15:   Herramientas de Modelamiento para el Control de Inventarios

  1. Herramientas de Modelamiento para el Control de Inventarios
  2. Control de Inventarios con Demanda desconocida

Capítulo 16:   Cadena de Markov

Capítulo 17:   Modelo de Insumo- Producto de Leontief

Capítulo 18:   Análisis de Costo Beneficio: Cantidad Económica

Capítulo 14:   Una Colección de Palabras y Frases Claves

Introducción

Modelos y Análisis de Decisiones con Periodos de Tiempo Crítico: La capacidad de modelar y realizar modelos de decisión y análisis es un rasgo esencial entre las muchas aplicaciones reales que van desde los tratamientos médicos de emergencia en las unidades de cuidados intensivos hasta en los sistemas de control de los comandos militares. Los formalismos y los métodos de inferencia existentes no han sido eficaces en las aplicaciones de tiempo real donde las compensaciones entre la calidad de decisión y manejabilidad computacional son esenciales. En la práctica, un acercamiento eficaz al modelamiento de decisión de tiempo dinámico crítico debería proporcionar el apoyo explícito al modelamiento de procesos temporales y al manejo de situaciones críticas de tiempo.

Uno de los elementos más importantes para un ejecutivo de alta gerencia es la capacidad de conducir su propia vida eficientemente, y luego modelar todas aquellas habilidades de liderazgo en los empleados de la organización.

La mayoría de las decisiones gerenciales están basadas en pronósticos. Cada decisión se hace efectiva en algún punto en el futuro, por lo tanto deberían estar basadas en pronósticos de las condiciones futuras.

Los pronósticos son necesarios en todas las áreas de una organización, y los mismos no deberían ser generadas por un grupo aislado de analistas. Tampoco se puede considerar ningún pronóstico como "terminado", los pronósticos son continuamente necesarios, y así como pasa el tiempo, el impacto de los pronósticos sobre el desempeño real de acontecimientos debe ser medido Llos pronósticos originales son actualizados y las decisiones son modificadas, y así sucesivamente. Este proceso es mostrado en la figura siguiente:

Los responsables de la toma de decisiones utilizan modelos de predicción como mecanismos de soporte en el proceso de toma de decisiones. Generalmente en la toma de decisiones se utilizan procesos basados en modelos, de manera de poder investigar el impacto de acciones retrospectivas en diferentes cursos; es decir "como si" la decisión ha sido tomada en un curso de acciones. Por esta razón, la secuencia de pasos en el proceso de modelado en la figura anterior debe ser considerada en orden inverso. Por ejemplo, los outputs (que es el resultado de la acción) debían ser considerados primero.

Es de suma ayuda el clasificar los componentes de la toma de decisiones en tres grupos: Incontrolable, Controlable, y Recursos (que definen la situación de problema.). Como es indicado en el cuadro de actividades anterior, el proceso de toma de decisiones tiene los siguientes componentes:

  1. Medida de comportamiento (o indicador, u objetivo): La medición del comportamiento del negocio es la prioridad para los gerentes. La gerencia para lograr objetivos funciona si se conocen los mismos. Lamentablemente, la mayoría de los gerentes no saben explícitamente lo que esto significa. El desarrollo de herramientas de medición de comportamiento eficientes han tornado gran importantes en casi todas las organizaciones. Sin embargo, los desafíos para lograr este objetivo en el sector público y en las organizaciones sin fines de lucro son difícilmente considerables. La medida de comportamiento proporciona el nivel deseable del resultado, es decir, el objetivo de su decisión. El tener un objetivo es importante para identificar la actividad de pronóstico. La tabla siguiente proporciona algunos ejemplos de medidas de comportamiento para diferentes niveles de gerencia:

    Nivel
    Medida de Comportamiento
    Estratégico  Retorno de la Inversión, Crecimiento, e Innovaciones
    Táctico  Costo, Cantidad, y Satisfacción al Cliente
    Operacional  Establecimiento de Objetivos, y Satisfacción de Estándares

    Obviamente, si se busca mejorar el sistema de comportamiento, lo que se está buscando es una visión operacional. Dicha interpretación indica como un sistema de pronóstico realmente trabaja tomando como ejemplo y referencia la correlación de los comportamientos de los resultados previos han generado. Es extremadamente importante entender como un sistema de pronóstico trabaja en la actualidad si se quiere cambiar como trabajará en el futuro. La actividad de pronosticar es un proceso iterativo. Este comienza con una planificación eficaz y eficiente, y termina en la compensación de otros pronósticos de acuerdo a la interpretación de su comportamiento.

  2. ¿Que es un Sistema? Los sistemas están formados por diferentes partes reunidas de una manera particular a fin de conseguir un objetivo. La relación entre las partes determina lo que el sistema hace y como funciona en general. Por lo tanto, habitualmente las relaciones entre un sistema son más importantes que las de cada una de las partes individualmente. En general, los sistemas son bloques de componentes básicos para otros sistemas llamados subsistemas.

    La Dinámica de un Sistema: Un sistema que no cambia es un sistema estático. Muchos de los sistemas económicos son sistemas dinámicos, lo cual significa que cambian a través del tiempo. Nos referimos al modo que un sistema cambia en el tiempo como el comportamiento del sistema. Cuando el desarrollo del sistema sigue un patrón de conducta típico, decimos que el sistema tiene un modelo de comportamiento. Sea cual sea el tipo de sistema estático o dinámico, esto dependerá del horizonte temporal y de las variables que sean usadas. El horizonte temporal es el período de tiempo dentro del cual se estudia el sistema. Las variables son valores cambiables sobre el sistema.

  3. Recursos: Los recursos son los elementos constantes que no se cambian durante el horizonte de tiempo del pronóstico. Los recursos son los factores que definen el problema de decisión. Las decisiones estratégicas tienen por lo general horizontes temporales más largos que las decisiones tácticas y operacionale.

  4. Pronósticos: Los valores de entrada del pronóstico están definidos por el entorno del que toma las decisiones. Los valores de entradas no controlables deben ser pronosticados o predichos.

  5. Decisiones: Los valores de decisión abarcan toda la colección de vías de acción que se puedan tomar.

  6. Interacción: Las Interacciones entre todos los componentes de decisión incluyen las funciones lógicas y matemáticas que representan las relaciones de causa-efecto entre los valores de entrada (insumos), recursos, pronósticos, y el resultado (outputs).

    7. Las interacciones son el tipo de relación más importante que se encuentran envueltas en el proceso de toma de decisiones. Cuando el resultado de una decisión depende del curso de acción, cambiamos uno o más factores del problema situacional con el objetivo de causar un cambio deseable en algún otro factor del mismo. Tendremos éxito si logramos conocer el comporamiento sobre la interacciones entre los componentes del problema.

    Adicionalmente, podría existir algún grupo de restricciones que se aplican a cada uno de estos componentes. Por lo tanto, no necesitan ser tratados separadamente.

  7. Acciones: La Acción es la decisión final y por lo tanto necesita la mejor estrategia para conseguir el objetivo deseable.

    8. La toma de decisiones implica la selección de un conjunto de acción (medios) para lograr los objetivos de los encargados de tomar decisiones (resultados.) La manera en la cual nuestro conjunto de acciones afecta el resultado de las decisiones dependerá de como de cómo el pronóstico y las otras variables de entrada se encuentren interrelacionadas y de la manera como las mismas se relacionan con el resultado.

Controlando el Problema de Decisión (Oportunidad): Pocos problemas en vida, una vez solucionados, permanecen de la misma manera. El cambiar condiciones tiende a deteriorar soluciones previamente encontradas, y sus soluciones crean nuevos problemas. Se necesita identificar y anticipar estos nuevos problemas.

Recuerde: Si no puede controlar algo, mídalo a fin de pronosticarlo o predecirlo..

El pronóstico es una predicción de lo que ocurrirá en el futuro, y esto es un proceso incierto. A causa de la incertidumbre, la exactitud del pronóstico es tan importante como el resultado predicho por el mismo. Este sitio web presenta una descripción general de las técnicas de pronóstico para negocios, las cuales se encuentran clasificadas en la figura siguiente:

Acercamiento Progresivo al Modelado: El Modelo para la toma de decisiones implica dos partes diferentes: Una es el ente encargado y con poder de toma de decisiones y el otro es el analista, el cual es el constructor del modelo. El analista debe asistir al tomador de decisiones en dicho proceso. Por lo tanto, el analista debe estar capacitado con más que un conjunto de métodos analíticos.

Toma de Decisiones Cuantitativa: Las Escuelas de Dirección y Gerencia de Negocios son cada vez más exitosas en la incorporación de mas y más estudiantes tomando programas de estudio a todo el nivel. En particular, existe un mercado creciente para cursos de conversión o cambios como Master en Dirección y Gerencia de Negocios, así como también en programas de post grado en Administración de Empresas (MBA.) En general, una fuerte base matemática no es un requisito imprescindible para la admisión a estos programas. Las percepciones del contenido se encuentran frecuentemente enfocadas en áreas de una buena comprensión funcional del negocio tales como en Mercadeo, Recursos Humanos, Contabilidad, Estrategia, Producción y Operaciones. La toma de decisiones cuantitativas, como pretende este curso, es un concepto desconocido, el cual es a menudo considerado como demasiado difícil y demasiado matemático. Obviamente, este curso puede jugar un papel importante para la formación de personas cursando estudios en programas de especialización en Dirección y Gerencia de Negocios, como por ejemplo en el área de Finanza.

A menudo, especialistas en la construcción de modelos tienden a estudiar un problema, y luego desarrollar de manera aislada un modelo matemático complicado para que sea usado por el gerente (es decir, el ente con poder de decisión.) Lamentablemente, el gerente podría no entender este modelo, por lo cual podría confiar y usar ciegamente en el o simplemente rechazarlo. El especialista podría pensar que el gerente es demasiado ignorante y poco sofisticado para apreciar el modelo, mientras que el gerente puede creer que el especialista vive en un mundo de ensueño de asunciones poco realistas y con un lenguaje matemático irrelevante.

Dicha falta de comunicación puede ser evitada si el gerente trabaja en conjunto con el especialista para desarrollar un modelo simple que proporcione un análisis ordinario pero comprensible. Después de que el gerente le ha tomado confianza al modelo, se podrían agregar detalles adicionales y un mayor grado de sofisticación, quizás de manera gradual. Este proceso requiere inversión de tiempo por parte del gerente y un interés sincero por resolver los problemas del gerente por parte del especialista, más que en la creación y explicación de modelos sofisticados. La construcción progresiva de este tipo de modelos es comúnmente referido al acercamiento de bootstrapping , el cual es el factor más importante para la determinación de una implementación exitosa de un modelo de decisión. Adicionalmente el acercamiento de bootstrapping simplifica la difícil tarea de validación y verificación de los procesos del modelo.

Modelos Efectivos para una Buena Toma de Decisiones

¿Qué es un modelo? Un Modelo es una representación externa y explícita de una parte de la realidad, el cual es visto por individuos que desean usarle para entender, cambiar, manejar y controlar esa parte de la realidad.

"¿Por qué se han diseñado tantos modelos y solo se usan unos pocos?" Esta es una pregunta discutida a menudo dentro de la comunidad del Modelamiento Cuantitativo (MC.) La formulación de la pregunta parece simple, pero los conceptos y teorías que deben ser manejados para darle una respuesta son mucho más sofisticados. ¿Existe un proceso de selección de "entre los muchos modelos diseñados"a "los pocos modelos utilizados?" Y de ser así, ¿cuales son las propiedades particulares que estos "pocos agraciados" tienen? Este sitio primero analiza varias definiciones de "modelos" presentados en la literatura de MC, y propone una síntesis de las funciones que un modelo puede manejar. Luego procede a definir el concepto de "realización", y progresivamente cambiamos de un modelo tradicional "de diseño a realización" como punto de partida a la teoría general de un modelo de diseño/ implementación, visto como un proceso de construcción cruzada entre el modelo y la organización en la cual es puesto en práctica. Por lo tanto, la organización no es considerada como un simple entorno, sino como un componente activo en el diseño de los modelos. Esto lógicamente conduce a seis modelos de implementación: el modelo tecnócrata, el modelo político, el modelo directivo, el modelo autodidacta, el modelo de conquista y el modelo experimental.

Obteniendo Éxito en la Implementación de un Modelo: A fin de que el analista tenga éxito en la realización de un modelo, el mismo debe tener tanto validez como ser legítimo, aquí están algunas pautas:

  1. Debe estar listo para trabajar en cooperación cercana con los diferentes agentes estratégicos con el objetivo de adquirir un entendimiento armonioso en el contexto organizacional. Adicionalmente, el MC debería tratar constantemente de discernir el grano de los valores de la organización desde sus partes más circunstanciales.

  2. El MC deberá intentar lograr un equilibrio entre el nivel de sofisticación y complejidad del modelo, así como también el nivel de competencia de los agentes participantes. El modelo debe ser adaptado tanto para la disponibilidad y para la capacidad cognoscitiva de los agentes participantes.

  3. El MC debería intentar hacerse familiar con las diversas preferencias prevalecientes en la organización. Esto es importante porque la interpretación y el uso del modelo variarán según las preferencias dominantes de los varios agentes dentro de la organización.

  4. El MC deberá asegurarse de que los posibles usos instrumentales del modelo estén bien documentados y que los agentes estratégicos en el proceso de toma de decisiones tengan suficiente conocimiento al respecto, así como también que se sientan confiados del contenido y funcionamiento del modelo.

  5. El MC debería estar preparado para modificar o desarrollar una nueva versión del modelo, y de ser necesario, hasta preparar un modelo completamente nuevo que permite una exploración adecuada de formulación de problema que fue imprevista, proporcionando nuevas alternativas de solución.

  6. El MC deberá asegurarse de que el modelo desarrollado proporciona una protección o holgura suficiente en el modelo para que los agentes participantes puedan ajustarse y reajustarse a las situaciones creadas por el modelo.

  7. El MC debería ser consciente con las ideas y conceptos preconcebidos por los agentes en cuanto a la definición del problema y las soluciones posibles; muchas decisiones al respecto podrían haber sido tomadas implícitamente mucho antes de que se hayan hecho explícitas.

En los modelos en los cuales se basan las tomas de decisiones, se esta particularmente interesado en la idea del diseño para la aplicabilidad de acciones.

Modelos descriptivos y prescritos: Un modelo descriptivo es a menudo una función de figuración y abstracción basada en la realidad. Sin embargo, un modelo prescrito lleva desde la realidad a un modelo una función del plan de desarrollo, los medios de acciones, y luego lo lleva desde el modelo devuelta a la realidad.

Es importante distinguir entre los modelos descriptivos y prescritos desde el punto de vista de la distinción del análisis tradicional entre el conocimiento y la acción. De hecho, los modelos prescritos son los puntos más lejanos en una cadena cognoscitiva, de predicción y de toma de decisiones.

¿Por qué el modelado? El objetivo de los modelos es ayudar a diseñar soluciones. Los mismos deben asistir al entendimiento del problema y ayudar a la deliberación y opción para permitirnos evaluar las consecuencias de nuestras acciones antes de ponerlos en práctica.

El principio de racionalidad asume que el tomador de decisiones es capaz de optimizar, pero sólo dentro de los límites de su representación del problema de decisión. Tal exigencia es absolutamente compatible con muchos resultados de la sicología de la memoria: Un experto usa estrategias recopiladas en su memoria a largo plazo y soluciona problemas de decisión específicos con la ayuda de su memoria de trabajo a corto plazo.

La solución de problemas es la toma de decisiones que envuelve heurísticas tales como el principio de satisfacción y disponibilidad. Esto implica evaluaciones generales de alternativas que podrían ser respaldadas por la memoria de trabajo a corto plazo, y la misma debería ser compatible con varias escalas de interés. La toma de decisiones podría ser vista como el logro de un proceso de información más o menos complejo, en el anclaje de la búsqueda de una estructura dominante: El tomador de decisiones actualiza su representación del problema con el objetivo de encontrar una alternativa que domine el resto de ellas, por ejemplo; en una aproximación matemática que se basa en sistemas dinámicos con tres principios básicos:

  1. Mezquindad: El tomador de decisiones usa cantidades pequeñas de la información.

  2. Confiabilidad: La información procesada es suficientemente relevante para justificar - personalmente o socialmente - resultados de decisión.

  3. Flexibilidad: La información procesada puede cambiar una decisión en otra.

La Ciencia Cognoscitiva nos proporciona un acercamiento a un sistema cognoscitivo, el cual en general es una asociación de un dispositivo físico en funcionamiento que es sensible a los cambios en el ambiente mediante la percepción y acción, con una visión que genera actividades mentales diseñadas tales como operaciones, representaciones, clasificaciones y/ o programas que conducen a estrategias eficientes para la resolución de problemas.

Las actividades mentales actúan sobre el ambiente, el cual reacciona en contra del sistema mediante la percepción producida por representaciones.

El diseño y realización de sistemas humanos centrados en la planificación, control, decisión y razonamiento requiere el estudio de las esferas operacionales de un sistema cognoscitivo en tres dimensiones:

Validación, y Verificación: Como la parte del proceso de calibración de un modelo, el modelador debe validar y verificar el modelo. El término validación es aplicado a estos procesos, el cual procura determinar si un modelo es correcto o no con respecto al sistema "real". En términos más comunes, la validación se encarga de responder la pregunta ¿Estamos construyendo el modelo correcto? "Por otra parte la verificación procura contestar la pregunta ¿Estamos construyendo el modelo correctamente?"

Balanceando el Éxito en los Negocios

Sin sistema métrico, la actividad de gerenciar podría estar en las nebulosas, si cree que es imposible, inténtelo. ¿Cómo podemos decir que hemos logrados nuestros objetivos si no sabemos cuales son? ¿Cómo sabemos si nuestras estrategias de negocio son eficientes si las mismas no han sido bien definidos? Por ejemplo, se necesita una metodología para medir el éxito y establecer objetivos desde la perspectiva financiera y operacional. Con este tipo de medida, cualquier negocio puede manejar su visión estratégica y ajustarla para cualquier cambio. El establecimiento de medidas de comportamiento es de perspectivas múltiples, al menos desde el punto de vista financiero, del cliente, de innovación, de aprendizaje, y de procesos internos de la compañía.

Obviamente, no es suficiente con producir un instrumento para documentar y monitorear el éxito. Sin una implementación y liderazgo apropiado, el crear una medida de comportamiento simplemente se mantendrá como un ejercicio mas que a un sistema para manejar el cambio.

Modelamiento para Pronósticos

El pronóstico es un insumo necesario para la planificación ya sea en un negocio o en el gobierno. Con frecuencia los pronósticos son generados de manera subjetiva y a un costo muy elevado para los grupos de discusión. Inclusive cuando métodos cuantitativos son relativamente simples, estos pueden por lo menos suministrar información para tales discusiones.

Recopilación de Datos para la Verificación de un Modelo: la Recopilación de datos es a menudo considerada "muy costosa". En efecto, la tecnología "relaja" sumente en el sentido de que cada vez nos hacemos mas dependientes de dispositivos y herramientas tecnológicas; Sin embargo, datos confiables son necesarios para verificar un modelo cuantitativo. Los modelos matemáticos, sin importar lo elegante o sofisticado que sean, algunas veces escapan de la apreciación del tomador de decisiones. En otras palabras, algunas personas piensan algebraicamente, mientras que otros hacen de manera geométrica. Cuando los datos son complejos o multidimensionales, existen buenas razones para trabajar con ecuaciones, aunque la apelación al intelecto tiene una connotación mas real: La belleza está a la vista de otros observadores - no a la vista suya, sino en udted mismo.

El organigrama siguiente destaca el desarrollo sistemático de las fases del modelado y el pronóstico:

Modeling for Forecasting

El organigrama anterior es útil para:

La Estadística para Pronóstico: La selección de la metodología para la implementación de pronóstico correcta siempre ha sido un asunto importante de planificación y control para la mayoría de las firmas y agencias. Con frecuencia, el bienestar financiero de toda la operación depende de la exactitud del pronóstico dado que dicha información será utilizada para tomar decisiones de presupuesto y de operación en áreas tales como gerencia de personal, compras, publicidad y mercadeo, financiamiento de capitales, etc. Por ejemplo, cualquier error de ventas realizada por arriba o por debajo del valor estimado podría generar problemas de costos de acumulación inventarios para la firma o perdidas en ingresos por desabastecimiento anticipado de inventarios. Cuando la demanda es relativamente estable, es decir, invariable o a una tasa creciente o decreciente constante, hacer un pronóstico mas preciso es menos complicado. Si por lo contrario la empresa presenta información histórica de alzas y bajas en los patrones de venta, la complejidad del trabajo de pronóstico es mucho mas complicado.

Existen dos aproximaciones básicas de pronóstico. La estimación de un valor futuro está basada en análisis de factores que, como se cree, influirán en valores futuros, es decir, el método explicativo o de predicción está basada en un estudio inferido de los comportamientos pasados de los datos, lo que esconocido como el método de extrapolación. Por ejemplo, la creencia que los niveles de venta corriente de ropa para muñecas aumentará debido a una campaña publicitaria reciente más bien que a la proximidad de la Navidad ilustra la diferencia entre las dos filosofías. Es posible que ambos acercamientos conduzcan a la creación de pronósticos exactos y útiles, pero se debe recordar que, hasta para un grado modesto de exactitud deseada, el método anterior es a menudo más difícil de validar y poner en práctica que el último.

Autocorrelación: la Autocorrelación es la correlación consecutiva de series de tiempo igualmente espaciadas entre sus miembros. Los términos alternativos son la correlación rezagada, y la persistencia. A diferencia de los datos estadísticos que son muestras aleatorias que nos permiten realizar análisis estadísticos, las series de tiempo son fuertemente autocorrelacionadas, haciendo posible la predicción y el pronóstico. Existen tres instrumentos para evaluar la autocorrelación de una serie de tiempo, estos son: la serie de tiempo de planificación , la planificación de rezagos, y por lo menos los primeros y segundos valores de orden de la autocorrelación.

A usted podría gustarle utilizar el Javascript Estadísticos de Series de Tiempo para realizar alguno de los cálculos estadísticos necesarios para una investigación preliminar de sus series de tiempo.

Series de Tiempo Estacionarias

La Estacionalidad siempre ha jugado un papel primordial en el análisis de series de tiempo. La mayoría de las técnicas para realizar pronósticos requieren condiciones de estacionalidad. Por lo tanto necesitamos algunas condiciones, es decir, las series de tiempo necesitan tener un proceso estacionario de primer y segundo orden.

Estacionario de Primer Orden: Una serie de tiempo esta en el estacionario de primer orden si el valor esperado de X(t) se mantiene constante para cualquier valor de t.

Por ejemplo, en series de tiempo económicas el proceso se encuentra en estacionario de primer orden cuando removemos cualquier tendencia por algún mecanismo como la diferenciación.

Estacionario de Segundo Orden: Una serie de tiempo se encuentra estacionaria de segundo orden solamente cuando la estacionaria de primer orden y la covarianza entre X(t) y X(s) es función de la anchura (t-s.)

De nuevo, en series de tiempo económicas, un proceso es estacionario de segundo orden cuando estabilizamos sus variables por cualquier tipo de transformación como la raíz cuadrada.

A usted podría gustarle en Javasript Prueba para Series de Tiempo Estacionarias

Sumario de Métodos de Pronóstico

De manera ideal, organizaciones que pueden financiar económicamente el pronosticar, asignan dichas funciones a departamentos específicos o a individuos que se encuentran bien calificados y que tienen los recursos disponibles necesarios para realizar los mismos bajo patrones de demandas complicadas. Obviamente la firma con mayor cantidad de operaciones y con un personal técnico que incluya estadísticos, científicos en gerencia, analistas de computadoras, etc. se encuentra en una mejor posición para seleccionar y darle el uso mas adecuado a las técnicas mas sofisticadas para realizar pronósticos, que como lo haría una compañía con recursos limitados. Notablemente, la compañía mas grande a través de su abundancia en recursos tiene ventajas competitivas sobre empresas mas pequeñas y puede esperarse que la misma sea mas diligente, efectiva y detallada a la hora de realizar pronósticos (a pesar de que las compañías mas pequeñas pueden soportar el mínimo de errores de cálculo a nuevos niveles de pronóstico.) A continuación especificamos algunas aproximaciones a pronósticos efectivos, especialmente para pronósticos y análisis a corto y mediano plazo:

Modelos Causales de Series de Tiempo: Cuando usamos regresiones múltiple, podemos utilizar mas de un factor de pronóstico. Esto siempre es lo mas recomendable. Sin embargo, el ser mezquino no es malo, es decir, se debe tratar de usar la menor cantidad de variables como pronosticadores posibles para obtener un pronóstico razonablemente preciso. La regresión múltiple es mejor utilizada cuando se utilizan paquetes comerciales tales como SAS ó SPSS. El pronóstico toma la forma de:

Y = b0 + b1X1 + b2X2 + . . .+ bnXn,

donde b0 es el intercepto, b1, b2, . . . bn son los coeficientes que representan la contribución de las variables independientes X1, X2,..., Xn.

El pronóstico es una predicción de lo que ocurrirá en el futuro, y esto es un proceso incierto. Dada la incertidumbre, la precisión de un pronóstico es tan importante como los resultados predichos por el pronóstico de las variables independientes X1, X2,..., Xn. Un sistema de control del pronóstico debe ser utilizado para determinar si la precisión del proceso se encuentra dentro de los limites aceptables. Existen dos métodos extensamente utilizados para controlar y monitorear pronósticos : El rastreo de señales y el de límites estadísticos de control .

Rastreo de Señal es calculado mediante la división de los residuos totales entre sus desviaciones absolutas medias (DAM). Para permanecer dentro de 3 desviaciones estándar, el rastreo de señal que esté dentro de 3,75 DAM normalmente se considera como suficientemente bueno.

Los Límites Estadístico de Control son calculados de manera similar al otro cuadro de limites de control de calidad, sin embargo, los residuos de la desviación estándar son utilizados.

Regresiones múltiples son utilizadas cuando están envueltos dos o más factores independientes, y para pronósticos de corto y mediano plazo. Estos son utilizados para evaluar cuales factores deben ser incluidos y cuales no, asi como también además para desarrollar modelos alternativos con diferentes factores.

Análisis de Tendencia: Este análisis utiliza regresión lineal y no lineal con el tiempo como la variable explicativa. Es utilizado donde los patrones con respecto al tiempo tiene tendencia a largo plazo. A diferencia de la mayoría de las series de tiempo, el análisis de tendencias no asume la condición de que las series de tiempo se encuentran espaciadas igualmente.

La regresión no lineal no asume una relación lineal entre las variables. Esta es usada frecuentemente cuando el tiempo es una variable independiente.

A usted podría gustarle utilizar en Javascript de Prueba para Detectar Tendencias.

En ausencia de "cualquier" tendencia visible, a usted también podría gustarle realizar la Prueba para la Aleatoriedad de las Fluctuaciones.

Modelando la Estacionalidad y la Tendencia: La estacionalidad es el patón de comportamiento que se repite para cada período. Por ejemplo los patrones anuales de estacionalidad tienen un ciclo de 12 períodos si los mismos corresponden a los meses, ó 4 períodos si son trimestres. Se requiere obtener una estimación del índice de estacionalidad para cada mes o cualquier otro período, ya sea bimestre, semana, etc. Dependiendo de la disponibilidad de los datos.

1. Indice de Estacionalidad: Este representa el grado en el cual la estacionalidad afecta a un segmento particular del año. El cálculo envuelve una comparación del valor esperado de un período específico con respecto a la media general.

El índice de estacionalidad mide en que grado en el cual el promedio de un período en particular se encuentra por arriba (o por debajo) de la media. Por lo tanto, para obtener una estimación precisa del índice de estacionalidad, se calcula el promedio del primer período del ciclo, el segundo período, etc., y se dividen por la media general. La formular para determinar el factor de estacionalidad es:

Si = Di/ D,

de donde:

Si = El índice de estacionalidad para el iésimo período,
Di = Los valores promedio de los n períodos,
D = La media general,
i = El iésimo período estacional del ciclo.

Un índice estacional de 1,00 para un mes en particular, indica que el valor esperado para ese mes 1/12 del promedio general de todos los meses. Un índice estacional de 1,25 indica que el valor esperado para ese mes en particular es 25% mayor que 1/12 del promedio general. Un índice estacional de 80 indica que el valor esperado para ese mes en particular es 20% menor que el 1/12 del promedio general.

2. Proceso de Desestacionalización: Desestacionalizar los datos, llamado también ajuste estacional, es el proceso mediante el cual se remueven variaciones recurrentes y periódicas en un entorno a corto plazo, es decir, semanas, trimestres, meses, etc. Por lo tanto, las variaciones estacionales son movimientos regulares repetidos en valores de series que pueden ligados a eventos recurrentes. Los datos desestacionalizados son obtenidos simplemente dividiendo cada observación de la serie de tiempo por el índice de estacionalidad correspondiente.

Casi todas las series de tiempo publicadas por el gobierno de los EEUU se encuentran desestacionalizadas usando el índice de estacionalidad para descifrar las tendencias subyacentes en los datos, los cuales podrían ser causados por factores de estacionalidad.

3. Pronósticos: La incorporación de la estacionalidad en los pronósticos es útil cuando las series de tiempo tiene tanto tendencia como componentes de estacionalidad. El ultimo paso en el pronóstico es utilizar el índice de estacionalidad para ajustar la proyección de la tendencia. Una manera simple de pronosticar utilizando los ajustes de estacionalidad es usando el factor de estacionalidad en combinación con una tendencia subyacente apropiada del valor total de los ciclos.

4. Una Aplicación Numérica: La tabla siguiente proporciona la información de ventas mensuales (en miles de $) deuna librería universitaria. Las ventas muestran un patrón de estacionalidad, con los valores mas altos cuando la universidad se encuentra en funcionamiento y decrece durantes los meses de verano.

M

T
Ene
Feb
Mar
Abr
May
Jun
Jul
Ago
Sep
Oct
Nov
Dic
Total
1
196
188
192
164
140
120
112
140
160
168
192
200
1972
2
200
188
192
164
140
122
132
144
176
168
196
194
2016
3
196
212
202
180
150
140
156
144
164
186
200
230
2160
4
242
240
196
220
200
192
176
184
204
228
250
260
2592
Media:
208,6
207,0
192,6
182,0
157,6
143,6
144,0
153,0
177,6
187,6
209,6
221,0
2185
Indice:
1,14
1,14
1,06
1,00
0,87
0,79
0,79
0,84
0,97
1,03
1,15
1,22
12


Suponga que deseamos calcular el factor de estacionalidad y la tendencia, luego calcular el pronóstico de las ventas para el mes de Julio en al año 5.

El primer paso en el pronóstico de estacionalidad será calcular los índices mensuales utilizando las ventas realizadas durante los 4 años previos. Por ejemplo, el índice para el mes de Enero:

S(Ene) = D(Ene)/D =208,6/ 181,84 = 1,14,

de donde D(Ene) es la media de todos los cuatro meses de Enero, y D es la media general de todas las ventas realizadas en los cuatro años previos.

Cálculos similares son realizados para cada otro mes. Todos los índices son totalizados en la última fila de la tabla anterior. Note que la media (el valor promedio) para los índices mensuales llega hasta 12, el cual es el número de períodos en un año para los datos mensuales.

A continuación una tendencia lineal es calculada utilizando las ventas anuales:

Y = 1684 + 200,4T,

La pregunta principal es si esta ecuación representa la tendencia.


Determinación de la Tendencia Anual para los Ejemplos Numéricos
Año No:
Ventas Realizadas
Regresión Lineal
Regresión Cuadrática
1
1972
1884
1981
2
2016
2085
1988
3
2160
2285
2188
4
2592
2486
2583


Muchas veces el colocar una línea recta en los datos estacionales es engañoso. Mediante la construcción de un diagrama de dispersión, podemos notar que una parábola proporciona una mejor representación. Utilizando el Javasript de la Regresión Polinomial, la tendencia cuadrática estimada es:

Y = 2169 - 284,6T + 97T2

Los valores predichos utilizando tanto en la tendencia lineal como en la cuadrática son presentados en la tabla anterior. Comparando los valores predichos de los dos modelos a los valores de los datos históricos, podemos identificar que la tendencia cuadrática proporciona un mejor ajuste que la lineal, lo cual es bastante común.

Ahora podemos pronosticar las ventas anuales siguientes, las cuales corresponden al año 5, ó t= 5 en la función cuadrática anterior:

Y = 2169 - 284,6(5) + 97(5)2 = 3171

Las ventas mensuales promedio durante el próximo año son: 3171/12 = 264,25.

Finalmente, el pronóstico para el mes de Julio es calculado multiplicando el promedio de las ventas mensuales por el índice de estacionalidad para el mes de Julio, el cual es 0,79; por lo tanto, (264,25)x (0,79) ó 209.

A usted podía gustarle utilizar el Javascript de Indice de Estacionalidad para comprobar sus cálculos manuales. Como siempre, usted debería utilizar primero Ploteo de Serie de Tiempo como una herramienta para el proceso de caracterización inicial.

Para probar la estacionalidad basada en los índices de estacionalidad, a usted podría gustarle utilizar el Javascript de Prueba para la Estacionalidad.

Eliminación de Tendencias y Análisis Cíclico: Los ciclos pueden ser estudiados fácilmente si la tendencia es removida. Esto se puede lograr expresando cada valor actual en la serie de tiempo como porcentaje de la tendencia calculada para los mismos datos. La serie de tiempo resultante no tendrá tendencia, pero oscilará alrededor de un valor central de 100.

Análisis de Descomposición: Este es el parámetro generado por las series de tiempo, los cuales no necesariamente son los valores de los datos individuales que son ofrecidos a los gerentes que son los observadores, planificadores o controladores del sistema. Por lo tanto, el análisis de descomposición es utilizado para identificar diferentes patrones que aparezcan simultáneamente en las series de tiempo.

Una gran variedad de factores pueden influir en los datos. Mientras se realice un estudio, es muy importante que las diferentes influencias o componentes sean separados o descompuestos de los niveles de datos "primarios." En general, existen cuatro tipos de componentes en el análisis de series de tiempo: Estacionalidad, Tendencia, Ciclos e Irregularidad.

Xt = St . Tt. Ct . I

Los tres primeros componentes son determinísticos, y son llamados "Signos", mientras que el último componente es una variable aleatoria llamada "Ruido." Para estar capacitado a realizar un pronóstico apropiado, necesitamos saber a que nivel cada componente esta incluido en los datos. Por lo tanto, para entender y medir estos componentes, el proceso de pronóstico primero envuelve el remover los efectos de los componentes fuera de los datos (descomposición.) Luego que los efectos son medidos, el pronóstico requiere que reincorporemos dichos componentes en las estimaciones del pronóstico. El proceso de descomposición de las series de tiempo es representado por el siguiente diagrama de flujo:

Time Series Decomposition Process

Definiciones cortas de los componentes principales del diagrama de flujo anterior:

Variación Estacional: Cuando un patrón repetitivo es observado sobre un horizonte temporal, se dice que la serie tiene un comportamiento estacionario. Los efectos estacionarios están asociados con los cambios en el calendario o climatológicos. Variaciones estacionales se encuentran atadas a ciclos anuales

Tendencia: Una serie de tiempo podría ser estacionaria o exhibir una tendencia temporal. Tendencias a largo plazo son normalmente modeladas bajos patrones de funciones lineales, cuadráticos o exponenciales.

Variaciones Cíclicas: Son movimientos hacia arriba o hacia abajo de la serie, los cuales no están asociados a variaciones estacionales. Normalmente resultan de variaciones en las condiciones económicas.

  1. Las Estacionalidades regularmente son fluctuaciones las cuales se repiten año tras año con duraciones e intensidades similares. El primer paso para la descomposición de una serie de tiempo es quitar los efectos estacionales en los datos. Sin desestacionalizar los datos, podríamos, por ejemplo, deducir incorrectamente que los patrones de incrementos recientes se mantendrán indefinidamente; es decir, una tendencia de crecimiento se encuentra presente, cuando realmente dicho incremento es simplemente obtenido " por la temporada del año"; es decir, debido a picos estacionales regulares. Para medir efectos estacionales, calculamos un grupo de índices estacionales. Un método práctico y extensamente usado para calcular estos índices es el acercamiento del "coeficiente a los promedios móviles." De acuerdo a este índice, podemos medir cuantitativamente a que distancia por encima o por debajo de un período determinado se esta con respecto al valor esperado o al "curso normal" del período con respecto a los datos (los datos esperados son representados por un índice de estacionalidad de 100% o de 1,0.)
  2. La Tendencia es el crecimiento, descenso o manutención de los datos en un período de tiempo determinado. Utilizando los datos desestacionalizados, nos gustaría considerar la tendencia de crecimiento como notamos en nuestra inspección inicial de las series de tiempo. La medición de los componentes de la tendencia se realiza simplemente ajustando una línea recta o algún otra función. Esta función ajustada se calcula mediante el método de los mínimos cuadrados y representa la tendencia general de todos los datos a través del tiempo.
  3. Los Ciclos generalmente son cambios en los datos representados por subidas y bajadas; estos cambios son generados, por ejemplo, en el entorno económico en general tales como recesiones y expansiones (no por efectos estacionales). Para medir como el efecto cíclico en general afecta los niveles de los datos, calculamos una serie de índices cíclicos. Teóricamente, los datos desestacionalizados todavía contienen restos de tendencias, ciclos y componentes irregulares. Adicionalmente, pensamos que los niveles en los datos predichos usando la formula de tendencia solo representan efectos de tendencia. Por lo tanto, se asienta una razón para que el cociente de estos valores de datos proporcionen un índice que refleje solo los componentes cíclicos e irregulares. Como el ciclo operativo de los negocios es por lo general mas largo que el ciclo estacional, se debería entender que el análisis cíclico no se espera que tan preciso como el análisis estacional.

    Debido a la enorme complejidad de los factores generales de comportamiento en la economía a largo plazo, una aproximación general a los factores cíclicos sería un objetivo mas realista. Por lo tanto, ni los picos positivos ni negativos serian nuestro interés principal sino la tendencia general de los efectos cíclicos que mueven gradualmente a cualquier dirección. Para estudiar el movimiento cíclico en general en vez de cambios cíclicos precisos (los cuales indican falsamente mayor precisión de la que realmente esta presente en esta situación), atenuamos los ploteos cíclicos cuando reemplazamos cada cálculo de índices con un promedio móvil de 3 períodos. El lector debería notar que a medida que el promedio del número de periodos móviles incrementa, los datos se hacen mas homogéneos y con diferencias mas atenuadas. La alternativa de 3 períodos, que podría ser considerada como subjetiva, puede ser justificada por el intento de atenuar todos los picos positivos y negativos de las acciones menores de los índices cíclicos, de manera que solo los cambios importantes permanezcan.

  4. Las Irregularidades(I) son cualquier fluctuación que no este clasificada en ninguna de las anteriores. Este es un componente inexplicable de las series de tiempo; por lo tanto son impredecibles. Las estimaciones de I solo pueden ser esperadas cuando su varianza no es demasiado grande. De lo contrario, no es posible descomponer las series. Si la magnitud de la variación es muy grande, la proyección de los valores futuros será imprecisa. La mejor alternativa es establecer intervalos probabilísticos para los valores futuros sujetos a que probabilidad dada de I es conocida.
  5. Haciendo Pronósticos: En este punto del análisis, luego de haber completado el estudio de los componentes de las series de tiempo, proyectamos valores futuros haciendo pronósticos para algunos períodos siguientes. El proceso se encuentra resumido a continuación:

    • Paso 1: Calcule el nivel de tendencia futura mediante la ecuación de tendencia.
    • Paso 2: Multiplique el nivel de tendencia obtenido en el paso 1 por el índice de estacionalidad de manera de incluir los efectos de estacionalidad.
    • Paso 3: Multiplique el resultado del paso 2 por el índice cíclico proyectado de forma tal que se incluyan los efectos cíclicos y se obtenga el pronóstico final.

Promedios Móviles Simples: El método de pronóstico mejor conocido es el de Promedios móviles o simplemente tomar un cierto número de períodos pasados, juntarlos, y luego dividirlos por el número de períodos. El método de Promedios Móviles Simples (PM) es un acercamiento eficaz y eficiente cuando las series de tiempo son estacionarias tanto en media como en varianza. La siguiente formula es utilizada para encontrar los Promedios móviles de orden n, PM(n) para un período t+1,

PMt+1 = [Dt + Dt-1 + ... +Dt-n+1] / n

de donde n es el número de observaciones utilizadas en los cálculos.

El pronóstico para el período t + 1 es el pronóstico para todos los períodos futuros. Sin embargo, este pronóstico es revisado cuando nuevos datos se encuentran disponibles.

A usted podría gustarle utilizar el JavaScript de Pronóstico por Atenuación, para luego realizar experimentaciones numéricas para una comprensión mas profunda de los conceptos.

Promedios Móviles Ponderados: son bastante poderosos y económicos. Son ampliamente utilizados donde los métodos de repetición de pronósticos son requeridos, tales como los métodos de suma de dígitos y ajuste de tendencias. Como un ejemplo de Promedios Móviles Ponderados:

PM Ponderado(3) = w1.Dt + w2.Dt-1 + w3.Dt-2

de donde las ponderaciones son cualquier número positivo tal que: w1 + w2 + w3 =1. una ponderación típica para este ejemplo es, w1 = 3/(1 + 2 + 3) = 3/6, w2 = 2/6, y w3 = 1/6.

A usted podría gustarle utilizar el JavaScript de Pronóstico por Atenuación, para luego realizar experimentaciones numéricas para una comprensión mas profunda de los conceptos.

Un ejemplo numérico ilustrativo: El promedio móvil y el ponderado móvil de orden cinco son calculados en la siguiente tabla:

Semana Ventas ( en miles de $) PM(5) PMP(5)
1 105 - -
2 100 - -
3 105 - -
4 95 - -
5 100 101 100
6 95 99 98
7 105 100 100
8 120 103 107
9 115 107 111
10 125 117 116
11 120 120 119
12 120 120 119

Técnicas de Atenuación Exponencial: Uno de los métodos de pronosticó mas exitosos es la técnica de atenuación exponencial (AE.) Mientras que el método de Promedios móviles simples es un caso especial del AE, este es mucho mas parsimonioso en el uso de los datos. Adicionalmente, puede ser modificado para ser utilizado de manera eficiente en series de tiempo con patrones de estacionalidad. También es relativamente fácil de ajustar de los errores pasados para el subsiguiente pronóstico, ideal para situaciones donde varios pronósticos deben ser preparados. Diferentes formas son utilizadas dependiendo de la presencia de variaciones cíclicas o de tendencias. En resumen, un AE es una técnica de promedio que utiliza pesos desiguales; sin embargo, las ponderaciones aplicadas a las observaciones pasadas decrecen en una forma exponencial.

Ft+1 = a Dt + (1 - a) Ft

de donde:

Dt e el valor actual
Ft es el valor pronosticado
a es el factor de ponderación, el cual oscila entre 0 y 1
t es el período de tiempo actual.

Note que el valor atenuado se convierte en el pronóstico para el período t + 1.

Un "a" pequeño proporciona un atenuante visible y detectable, mientras que cuando el "a" es grande, proporciona una respuesta rápida de los cambios recientes en la serie de tiempo, y un monto mas pequeño de atenuaciones. Note que las técnicas de atenuación exponencial y de Promedios móviles simples generarán pronósticos con el mismo promedio de tiempo siempre que el promedio móvil de orden n sea la parte entera de (2-a)/a.

Una atenuación exponencial sobre una serie de tiempo ya atenuada con anterioridad es llamada atenuación exponencial doble. En algunos casos seria necesario extender este proceso hasta una atenuación exponencial triple. Mientras que la atenuación exponencial simple requiere de la condición de inmovilidad (estacionaria), la atenuación exponencial doble podría capturar tendencias lineales, y la atenuación exponencial triple puede manejar casi todas las demás series de tiempo del negocio.

Las técnicas de atenuación, tales como la de Promedios móviles y atenuación exponencial son satisfechas para pronósticos con un período por anticipado, tal y como es implementado en el siguiente Javascript: Pronóstico por Atenuación .

El filtraje de datos es una herramienta efectiva y eficiente para el modelamiento de series de tiempo cuando se aplican las técnicas de transformación apropiadas. La mayoría de las técnicas de análisis de series de tiempo envuelven algunas formas de filtraje de ruido con el objetivo de hacer los patrones de comportamiento mas obvios.

Diferenciación: Un tipo especial de filtraje, el cual es particularmente especial para remover tendencias, es simplemente diferenciar una serie de tiempo dada hasta que se convierta estacionaria. Este método es útil en el modelamiento de la Box-Jenkins. Para datos no estacionales, la diferenciación de primer orden es normalmente suficiente para alcanzar una estabilidad aparente, de manera tal que las nuevas series estén formadas de las series originales.

Filtraje Adaptativo Cualquier técnica de atenuación tal como la de Promedios móviles la cual incluye el método de aprendizaje por errores pasados que pueden responder a cambios en la tendencia, estacionalidad y factores aleatorios de relativa importancia. En el método adaptativo de atenuación exponencial, se podría ajustar a para permitir los cambios en patrones de comportamiento.

Filtro de Hodrick-Prescott: Este es un mecanismo de atenuación utilizado para obtener los componentes de tendencia a largo plazo en las series de tiempo. Esta es una manera de descomponer una serie de tiempo dada sus componentes estacionarios y no estacionarios de tal manera que la suma de los cuadrados de la serie de los componentes no estacionarios sea mínima con una penalidad sobre los cambios derivativos de los mismos.

Filtro de Kalman: El filtro de Kalman es un algoritmo para la actualización secuencial de una proyección lineal en un sistema dinámico el cual esta representado en una fase espacial. Las aplicaciones del filtro de Kalman son las de transformar el sistema de una representación de las dos formulas siguientes a una forma mas razonable:

x t+1=Axt+Cw t+1, y yt=Gxt+vt en el cual: A, C, y G son matrices conocidas como funciones del parámetro q sobre el cual la inferencia es deseada donde: t es un número entero, usualmente el tiempo indexado; xt es una variable de estado verdadero, escondido de los econometristas; yt es una medición de x con un factor escalado G, y los errores de medición yt, wt son innovaciones a los procesos escondidos xt, E(wt+1wt')=1 por normalización (donde, ' significa la transpuesta), E(vtvt)=R, una matriz desconocida, una estimación la cual es necesaria pero es auxiliar al problema de interés, el cual es el obtener una estimación de q. El filtro de Kalman define dos matrices St y Kt de forma tal que el sistema descrito anteriormente puede ser transformado en el siguiente, en el cual las estimaciones e inferencias sobre q y R son mas directas, es decir, mediante el análisis de regresión:

zt+1=Azt+Kat, y yt=Gzt+at de donde zt esta definida a ser Et-1xt, at esta definida a ser yt-E(yt-1yt, y K esta definida a ser el límite Kt cuando t se acerca al infinito.

La definición de estas dos matrices St y Kt es en si misma la definición de los filtros de Kalman: Kt=AStG'(GStG'+R)-1, y St-1=(A-KtG)St (A-KtG)'+CC'+Kt RKt' , Kt es comúnmente llamada la ganancia de Kalman.

Redes Neurales: Para el pronóstico de series de tiempo, el modelo de predicción de orden p, tiene la forma general:

Dt=f(Dt-1, Dt-1,..., Dt-p) + et

Las arquitecturas de redes neurales pueden ser entrenadas para predecir los valores futuros de las variables dependientes. Los requerimientos son el diseño del paradigma de la red y sus parámetros. El acercamiento de redes neurales de retroalimentación de capas múltiples consiste en una capa de entrada, una o varias capas escondidas y una capa de salida o resultado. Otro acercamiento es conocido como la red neural parcialmente recurrente, la cual puede aprender secuencias a medida que el tiempo transcurre y responde de manera diferente a los mismos patrones de estímulos de entrada a diferentes períodos de tiempo, dependiendo por supuesto de los distintos patrones de entrada. Ninguno de estos acercamientos es superior a cualquiera de los otros en cualquiera de los casos; sin embargo, una retroalimentación empapada que posea las características de una memoria dinámica, mejorará el funcionamiento de ambos acercamientos.

Consideraciones de Outlier: Los outliers son algunas observaciones que no son bien ajustadas por el "mejor" modelo disponible. En la práctica, cualquier observación con residuos estandarizados con valor absoluto mayores a 2,5 es un candidato para ser considerado un outlier. En estos casos, se debería primero investigar el origen de los datos. Si no existe ninguna duda sobre la precisión o veracidad de las observaciones, entonces debería ser removido, y el modelo debería ser reajustado.

Siempre que los niveles de los datos sean considerados muy altos o muy bajos con respecto a los valores "usuales en el negocio", llamamos a estos valores outliers. Una razón matemática para ajustar estas ocurrencias es que la mayoría de las técnicas de pronóstico están basadas en promedios. Es bien sabido que las medias aritméticas son muy sensibles a los valores de los outliers; por lo tanto, algunas alteraciones en los datos deberían ser hechas antes de continuar. Una aproximación seria el reemplazar el outlier por el promedio de los dos niveles de ventas para los períodos, los cuales vienen inmediatamente antes y después del período en cuestión, y luego poner este número en el lugar del outlier. Esta idea es util siempre que el outlier ocurre a la mitad o en una parte reciente de los datos. Sin embargo, si los outliers aparecen en la parte mas antigua de los datos, se debería seguir una segunda alternativa, la cual es simplemente eliminar los datos e incluir los outliers.

En la ligereza de la relativa complejidad de algunas técnicas sofisticadas de pronóstico, nosotros recomendamos que la gerencia se dirija a través de una progresión evolucionaria para adoptar nuevas técnicas de pronóstico. Esto significa que, es mejor que sea implementado un modelo de pronóstico simple bien entendido que a otro con todos los despliegues y presentaciones, pero que sea confuso en muchas facetas.

Modelamiento y Simulación: Los modelamientos y simulaciones dinámicas son la habilidad colectiva para entender el sistema y las implicaciones de sus cambios a través del tiempo, incluyendo el pronóstico. Los sistemas de simulación son una mímica de la operación del sistema real, tal como las operaciones diarias de un banco, o el valor de una determinada acción en la bolsa de valores durante un periodo de tiempo especifico. Mediante las corridas de simulación para avanzar en decisiones futuras, los gerentes pueden encontrar fácilmente como el sistema podría comportarse en el futuro, por lo tanto, las decisiones podrían ser juzgadas como apropiadas.

En el campo de las simulaciones, el concepto del "principio de la equivalencia computacional" tiene implicaciones favorables para los tomadores de decisiones. Las experimentaciones simuladas aceleran y reemplazan efectivamente la ansiedad de "esperar para ver que sucede" descubriendo nuevas formas y explicaciones para comportamientos futuros del sistema real.

Modelos Probabilísticos: El uso de técnicas probabilísticas, tales como los Métodos de Investigación de Mercadeo, para lidiar con incertidumbre, ofrece un rango de resultados probables para cada grupo de eventos. Por ejemplo, se podría desear identificar los prospectos compradores de un nuevo producto dentro de una comunidad de tamaño N. De el resultado de una encuesta, se podría estimar la probabilidad de vender p, y luego estimar el tamaño de las ventas totales Np con un cierto nivel de confianza.

Una Aplicación: Suponga que deseamos pronosticar las ventas de una nueva pasta de dientes en una comunidad de 50.000 amas de casas. Una muestra gratis es suministrada a 3.000 de ellas que fueron seleccionadas de manera aleatoria, y luego 1.800 de ellas indicaron que comprarían el producto.

Utilizando la distribución binomial con parámetros (3000, 1800/3000), el error estándar es 27, y las ventas esperadas son 50000(1800/3000) = 30000. El intervalo de confianza de 99,7% se encuentra dentro de 3 veces el error estándar 3(27) = 81 veces el coeficiente de la población total 50000/3000; es decir, 1350. En otras palabras, las ventas esperadas se encuentran entre un rango de (28650, 31350).

Análisis de Eventos Históricos: Algunas veces los datos para un período explicito de un evento (o eventos) en particular se encuentran disponibles, por ejemplo, en un grupo de pacientes. Algunos ejemplo de eventos podrían incluir ataques de asma; de epilepsia; infartos al miocardio; admisiones al hospital, etc. Generalmente, las ocurrencias (y no ocurrencias) de un evento se encuentran disponibles en condiciones normales (por ejemplo, diarios) los datos podrían ser pensados como si tuvieran una estructura de medición. Un objetivo podría ser el determinar si un evento o medición concurrente han influenciado en la ocurrencia del evento en que estamos interesados. Por ejemplo, la generación diaria de polen podría influenciar en el riesgo de ataques de asma; la presión alta en la sangre podría preceder a un infarto en el miocardio. Se podrían utilizar el PROC GENMOD, el cual esta disponible en SAS para el análisis de eventos históricos.

Números Indices: Un número índice mide el valor de una serie de tiempo en un período de tiempo (normalmente como porcentaje) con respecto a un período base.

Para una aplicación de números índices para pronósticos, considere el siguiente ejemplo simple (para ahorrar espacio):

Indices Compuestos: Considere el costo total de materiales para una planta industrial A, como se muestra en la tabla siguiente:

   
Año 2000
Año 2001
  Unidades Necesitadas
Costo por Unidad
Total
Costo por Unidad
Total
Mano de Obra
 20
10
200
 11 220
Aluminio
 02
100
200
 110 220
Electricidad
 02
50
100
 60 120
Total
500
560

De la información obtenida en la tabla anterior, el índice para los dos años consecutivos son 500/500 = 1, y 560/500 = 1,12, respectivamente. En vez de calcular el índice para cada año utilizando el año base, se podrían presentar los resultados graficando los índices con respecto al tiempo como una serie de tiempo para propósitos de pronóstico.

Pronosticando la Respuesta de los Mercados: Como parte de las investigaciones aplicadas a la economía y a los negocios, los cuales se enfrentan a la tarea de predecir la respuesta de los mercados, raras veces sabemos la forma funcional de las respuestas. Quizás las respuestas de los mercados son una función no lineal monótona, o simplemente una función no monótona de variables explicativas. Quizás es determinada por las interacciones de las variables explicativas. La interacción es lógicamente independiente de sus componentes.

Cuando tratamos de representar relaciones complicadas entre mercados dentro del contexto de un modelo lineal, usando transformaciones apropiadas de variables explicativas y de respuesta, aprendemos cuan difícil puede ser el trabajo estadístico. Encontrar modelos razonables es todo un reto, y justificar nuestros modelos alternativos a nuestros colegas puede ser mucho mas desafiante. Abundan las especificaciones alternativas.

Los métodos modernos de regresión, tales como los modelos aditivos generalizados, regresiones adaptativas simples de variación múltiple, y los árboles de regresión tienen una clara ventaja: Ellos pueden ser usados sin una forma funcional por adelantado. Estos métodos adaptativos intensivos en el uso de computadoras, ofrecen un acercamiento al modelamiento mas flexible que los métodos estadísticos tradicionales. ¿Que tan bien funcionan los métodos modernos de regresión en la predicción de la respuesta de los mercados? Algunos funcionan perfectamente fundamentados en los resultados de los estudios de simulación.

Análisis de Delphi: Este método es utilizado en el proceso de toma de decisiones, en particular en el pronóstico. Muchos "expertos" se reúnen y tratan de comprometerse en algo sobre el cual no pueden ponerse de acuerdo.

Combinación de Pronósticos: La combinación de pronósticos fusiona varios grupos separados de pronósticos para lograr una mejor composición de los mismos. La pregunta aquí es: ¿Como encontrar la combinación de ponderación óptima? El acercamiento comúnmente utilizado es cambiar las ponderaciones de vez en cuando para mejorar el pronóstico en vez de utilizar un grupo fijo de ponderaciones en condiciones normales.

Todos los modelos de pronóstico tienen una estructura de error ya sea explicita o implícita, donde el error es definido como la diferencia entre el modelo de predicción y el valor "verdadero." Adicionalmente, muchas metodologías de rastreo de datos dentro del campo de la estadística necesitan ser aplicadas a datos proporcionados a los modelos de predicción. La comprobación diagnóstica también, como es definida en el campo estadístico, es requerido para cualquier modelo que utilice datos.

Cuando se utilice cualquier modelo de pronóstico se deben realizar mediciones de manera de asegurar la calidad del método. La Desviación Absoluta Media (DAM), y la Varianza son las medidas mas utilizadas. Sin embargo, la DAM no se presta para realizar mayores inferencias, pero el error estándar sí. Para los propósitos de análisis de errores, la varianza es preferida porque la varianza de errores independientes (no relacionados) son aditivos; sin embargo, la DAM no es aditiva.

La Regresión y los Promedios Móviles: Cuando una serie de tiempo no es una línea recta se podrían utilizar los Promedios móviles (PM) y romper la serie de tiempo en varios intervalos con líneas rectas comunes de pendientes positivas, de manera de lograr la linealidad de toda la serie de tiempo. El proceso envuelve la transformación basada en la pendiente y luego el promedio móvil dentro de ese intervalo. Para la mayoría de las series de tiempo de negocios, la siguiente transformación podría ser efectiva:

Como Hacer Pronósticos Mediante el Análisis de Regresión

Introducción

La regresión es el estudio de la relación entre variables con el objetivo principal de predecir o estimar el valor de una variable con respecto a otras variables conocidas o de valores asumidos, las cuales se encuentran relacionadas a ella.

Variables de Interés: Para realizar estimaciones o predicciones, se debe primero identificar los estimadores apropiados para la variable de interés: ¿Cuáles variables son indicadores importantes?, ¿Pueden ser estas variables medidas al menor costo posible?, ¿Cuales de ellas proporcionan poca información? y ¿Cuáles son variables redundantes?

Prediciendo el Futuro Predecir un chance a través del tiempo o explorando desde las condiciones actuales a las condiciones futuras no es parte del análisis de regresión. Para hacer estimaciones sobre el futuro, usted debería utilizar el análisis de series de tiempo.

Experimento: este comienza con una hipótesis referente a como varias variables podrían estar relacionadas con otras variables, y del tipo de relación.

Regresión Lineal Simple: Una regresión que utiliza solo un pronosticador o estimador, es llamada regresión simple.

Regresión Múltiple: Cuando existen dos o mas estimadores se utiliza el análisis de regresión múltiple.

Data: Por que obtener información de una población entera es simplemente irrealista, una muestra siempre es escogida, la cual es un subconjunto de la población. Por ejemplo, una muestra podría ser igualmente escogida al azar o tomando los valores x dependiendo de la capacidad que tienen los equipos de experimentación que utilizan los investigadores. Cuando los valores x son preseleccionados y dependiendo de los mismos, solo inferencias limitadas pueden ser obtenidas. Cuando x e y son seleccionadas aleatoriamente, las inferencias pueden ser generalmente obtenidas dentro de un rango de valores en la muestra.

El Diagrama de Dispersión: Es una representación gráfica de pares de datos, los cuales pueden ser dibujados para obtener una visión general del problema. ¿Existe una relación aparente entre las variables?, ¿Directa?, ¿Inversa? Si los puntos descansan sobre una banda descrita por dos líneas paralelas, podríamos decir que existe una relación lineal entre los valores de x e y. Si la tasa de cambio no se mantiene constante en general, podríamos decir que los datos siguen una relación de forma curva.

El Modelo: Si hemos determinado que existe una relación lineal entre t e y, queremos obtener una ecuación lineal que establezca a y como función de x en la forma de Y = a + bx + e, de donde a es la intercepción, b es la pendiente y e es la medida de error para todas las variables que afectan y, pero que no son incluidas como factores de predicción y/ó factores impredecibles o incontrolables.

Método de los Mínimos Cuadrados: Para predecir la media del valor de y para un valor x determinado, se necesita una línea que pase a través de todos los valores medios de x e y, y que minimice la suma entre las distancias de cada uno de los puntos y la línea de predicción. Este acercamiento debería resultar en una línea que podríamos decir que "ajusta mejor" a los datos de la muestra. El método de los mínimos cuadrados alcanza este resultado mediante el cálculo del promedio mínimo al cuadrado de las desviaciones entre la muestra y la línea estimada. Un procedimiento es utilizado para encontrar los valores de a y b, la cual se reduce a la solución de ecuaciones lineales simultaneas. Se han desarrollado formulas para acortar los pasos para encontrar soluciones alternativas de ecuaciones simultaneas.

Métodos de Solución: Las Técnicas de Álgebra Matricial pueden ser empleadas de manera manual para resolver ecuaciones lineales simultáneas. Esta técnica es útil especialmente cuando existen sistemas de dos o mas ecuaciones con dos variables desconocidas.

Existen numerosos paquetes de computadoras disponibles que pueden ser utilizados para aliviar los problemas computacionales del trabajo de resolver ecuaciones lineales y polinomiales: el paquete Programas Biomédico de Computadoras (BMD, Biomedical Computer Programs) de la UCLA; el Paquete Estadístico para Ciencias Sociales (SPSS, Statistical Package for the Social Sciences) desarrollado por la Universidad de Chicago; y el Sistema de Análisis Estadístico (SAS, Statistical Analysis System). Adicionalete existe otro paquete disponible llamado Biblioteca Internacional de Matemáticas y Estadística (IMSL, the International Mathematical and Statistical Libraries), el cual contiene una extensa variedad de cálculos matemáticos y estadísticos estándares. Todos estos paquetes utilizan álgebra matricial para resolver ecuaciones simultaneas.

Utilidad e Interpretación de la Ecuación de Regresión: la ecuación desarrollada puede ser utilizada para predecir un valor promedio sobre el rango de los datos de la muestra. Se puede considerar que el pronóstico es bueno por un rango que va de corto a mediano plazo de tiempo.

Midiendo el Error de la Estimación: La dispersión o variabilidad alrededor de los valores de la media pueden ser medidos mediante el cálculo de la varianza, el promedio de la desviación al cuadrado de los valores alrededor de la media. La estimación del error estándar es derivada mediante la raíz cuadrada de este valor, y es interpretado como la medida promedio en la cual los valores reales difieren de la media estimada.

Intervalo de Confianza: La estimación de intervalos puede ser calculada para obtener una medida de la confianza que tenemos en la existencia de relación en nuestra estimación. Estos cálculos se realizan utilizando la tabla de distribución t. De estos cálculos podemos derivar bandas de confianza, un par de líneas no paralelas ubicadas lo mas cercanas posible a los valores medios que expresan nuestra confianza a varios grados de la banda de valores alrededor de la ecuación de regresión.

Evaluación: ¿Que tan confiados podemos estar de que realmente existe una relación? La rectitud de la relación puede ser evaluada mediante la prueba estadística de hipótesis, tal como la hipótesis nula, la cuales son establecidas usando la distribución t, el R cuadrado, las tablas de la distribución F. Estos cálculos incrementan el error estándar del coeficiente de regresión, una estimación del coeficiente de regresión b variará de muestra a muestra de igual tamaño dentro de la misma población. Un Análisis de la Tabla de Varianza (ANOVA) puede ser generada, la cual resume los diferentes componentes de variación.

Cuando se quiere comparar modelos de tamaños diferentes (Diferente número de variables independientes y/ o tamaño de muestra diferente) se tiene que utilizar el R cuadrado ajustado porque el R cuadrado típico tiende a crecer con el número de variables independientes.

El Error Estándar de un Estimador, por ejemplo, la raíz cuadrada de las medias al cuadrado, es un buen indicador de la "calidad" de un modelo de predicción porque "ajusta" la Suma de los Errores Medios al Cuadrado (SEMC) para el número de predictores en el modelo, como sigue a continuación:

SEMC = Suma de los Errores Medios al Cuadrados/ (N - Número de Predictores Linealmente Independientes)

Si continuamos agregando predictores al modelo, el SEMC se convertirá menos estable. El R cuadrado también esta influenciado por el rango de los valores dependientes; por lo tanto, si dos modelos tienen la misma media residual al cuadrado, pero uno de ellos posee un rango mas pequeño de valores para la variable dependiente, dicho modelo tendrá un R cuadrado más grande. Esto explica el hecho de que ambos modelos trabajarán perfectamente para los propósitos de predicción.

A usted podría gustarle utilizar el JavaScript de Análisis de Regresión con Instrumentos Diagnósticos para comprobar sus cálculos, y para realizar algunas experimentaciones numéricas para una compresión mas profunda de estos conceptos.

Planificación, Desarrollo, y Mantenimiento de un Modelo Lineal

A. Planificación:

  1. Defina el problema; seleccione respuestas; sugiera variables.

  2. ¿Son las variables seleccionadas fundamentales para el problema, y son ellas verdaderas variables? ¿Son dichas variables mesurables/ contables? ¿Se podría obtener un conjunto de observaciones al mismo momento? Ordinariamente, el análisis de regresión no asume que las variables independientes son medidas sin errores. Sin embargo, estas se encuentran condicionadas a cualquier error que pueda ocurrir o estén presentes en el conjunto de datos independientes.

  3. ¿Es el Problema potencialmente solucionable?

  4. Encuentre la matriz de correlación y las primeras corridas de la regresión (para unos datos seleccionados.)
    Encuentre los estadísticos básicos, matriz de correlación.


    ¿Qué tan difícil es el problema? Calcule el Factor de Inflación de la Varianza:

    FIV = 1/(1 -rij), para todos los i, j.

    Para un FIV, digamos entre 2 y 8, usted podría ser capaz de desarrollar un "buen" modelo.

    Inspeccione rij; por lo menos uno o dos tienen que ser grandes. Si todos son pequeños, quizás el rango de las variables X son muy pequeños.

  5. Establezca objetivos, prepare una restricción (o un presupuesto) y tablas de tiempo.

    a. La ecuación final debería contener: R2 Ajustado = 0,8 (por ejemplo).
    b. El Coeficiente de Variación digamos, menor que 0,10
    c. El número de predictores no debería exceder a p (digamos, 3), (por ejemplo para p = 3, se necesitan 30 puntos por lo menos.) Igualmente si todas las asunciones generales del modelo de regresión son satisfechas, el sobre ajuste podría arruinar la utilidad del modelo. El acercamiento mas usado es el método de reducción de datos para trabajar con los casos donde el número de predictores potenciales es grande si se compara con el número de observaciones.
    d. Todos los coeficientes estimados deben ser significativos a un nivel de digamos m = 0,05 (por decir algo).
    e. No existen patrones en los residuos

  6. ¿Son los objetivos y las restricciones (o presupuestos) aceptables?

B. Desarrollo del Modelo:

  1. Colecte los datos; verifique la calidad de los datos; plotee; pruebe los modelos; verifique las condiciones de regresión.

  2. Consulte a los expertos para obtener críticas.
    Introduzca una nueva variable y examine el mismo modelo ajustado. Adicionalmente las variables predictores transformadas deberían ser utilizadas.

  3. ¿Se han logrado los objetivos?
    ¿Ha encontrado "el mejor" modelo?

C. Validación y Mantenimiento del Modelo:

  1. ¿Son los parámetros estables dentro del espacio muestral?

  2. ¿Existe una deficiencia en el ajuste?
    ¿Son los coeficientes razonables? ¿Existen algunas variables obvias ausentes? ¿Es la ecuación aplicable para realizar controles o para predicciones?

  3. Mantenimiento del Modelo.
    Se necesita tener control el siguiente diagrama para verificar periódicamente el modelo mediante técnicas estadísticas.

Regression Analysis Process

Proceso de Análisis de Regresión
Haga clic en la imagen para agrandarla, y LUEGO imprímala

A usted podría gustarle utilizar el Análisis de Regresión con Instrumentos Diagnósticos cuando realice análisis de regresión.

Metodología de Transferencia de Funciones

 Es posible extender el modelo de regresión a una representación dinámica entre variables mediante una apropiada función de transferencia que es utilizada en la construcción de esquemas de acción y reacción. El modulo del Analizador de Función de Transferencia en el paquete de computadora para modelamiento y pronóstico SCA es un paquete de espectro de análisis de frecuencia diseñado con la ingeniería en mente. El mismo aplica el concepto de transformación integral de Fourier a un grupo de datos de entrada para proveer una representación global de frecuencia de una función aproximada por los datos de entrada. Adicionalmente presenta los resultados en términos de ingeniería convencionales.

Prueba para una Estimación de Cambios Estructurales Múltiples

 Las pruebas para brechas estructurales que mi experiencia me ha permitido ver estan diseñadas para detectar solo una brecha en la serie de tiempo. Esto es cierto siempre que el punto de brecha es conocido o estimado mediante el uso de métodos iterativos. Por ejemplo, para probar cualquier cambio en el nivel de las series dependientes o modelos de especificación, se debería utilizar una prueba iterativa para determinar puntos temporales mediante la incorporación de variables de cambios de nivel (0,0,0,0,...,1,1,1,1,1) para medir los cambios en la intercepción. Otras causas son los cambios en la varianza y en los parámetros.

Metodología de la Box-Jenkins
Introducción

Basamentos de los Pronósticos: La idea básica detrás de los modelos de pronóstico de series de tiempo auto proyectados es el encontrar una formula matemática que genere de forma aproximada los patrones históricos de las series de tiempo.

Series de Tiempos: Una serie de tiempo es un grupo de números que miden el estatus de alguna actividad en particular a través del tiempo. Es el registro histórico de algunas actividades, con mediciones hechas en intervalos iguales de tiempo (excepto mensualmente), manteniendo una consistencia en la actividad y el método de medición.

Acercamiento al Pronóstico de Series de Tiempo: existen dos acercamientos básicos para pronosticar series de tiempo: la auto proyección de series de tiempo y el acercamiento de causa-efecto. Este último método intenta pronosticar basado en series subyacentes las cuales se cree que causan comportamientos o influyen a las series originales. La auto proyección de series de tiempo solo emplea los datos de la serie de tiempo de la actividad a ser pronosticada para realizar el mismo. Este último acercamiento es en general menos costoso para su aplicación, requiere mucho menos datos y es útil solo para periodos de pronóstico de corto a mediano plazo.

Método para Pronóstico de la Box-Jenkins: la versión de variación única de esta metodología es el método de auto proyección de series de tiempo. El objetivo subyacente es encontrar una formula apropiada de forma tal que los residuos son lo mas pequeño posible y que no exhiben ningún patrón. El proceso de construcción del modelo envuelve algunos pocos pasos que son repetidos tantas veces sea necesario de manera de finalizar con una formula específica que reproduce los patrones de la serie de tiempo tan cerca como sea posible, y que adicionalmente representa un pronóstico preciso.

Metodología de la Box-Jenkins

Los modelos de pronóstico de la Box-Jenkins se basan en conceptos y principios estadísticos, y son capaces de modelar un amplio espectro de comportamiento de series de tiempo. Posee diferentes clases de modelos para escoger además de un acercamiento sistemático para elegir el modelo correcto. Incluye tanto pruebas estadísticas para la validación de modelos, así como también mediciones estadísticas para pronosticar incertidumbre. En contraste, los modelos de pronóstico tradicionales ofrecen un número limitado de modelos relativos debido al comportamiento complejo de muchas series de tiempo, con escasas pautas y pruebas estadísticas para la verificación de la validez del modelo seleccionado.

Datos: La falta de uso, la incomprensión, y la falta de precisión de los pronósticos son a menudo el resultado de no apreciar la naturaleza de los datos que se tienen disponibles. La consistencia de los datos tiene que ser asegurada, y se debe tenerse claro que representan y como fueron obtenidos o calculados. Como una regla empírica, la Caja de Jenkins requiere de por lo menos 40 ó 50 periodos igualmente espaciados de datos. Adicionalmente, los datos tienen que estar editados para lidiar con valores omitidos, extremos u otra distorsión ocasionada por el uso de funciones tales como log o inversa, de manera de alcanzar la estabilización.

Procedimiento de Identificación del Modelo Preliminar: Un análisis preliminar de la Box-Jenkins con ploteo en los datos iniciales debería ser corrido como el punto de inicio en la determinación del modelo apropiado. Los datos de entrada deben estar ajustados para formar una serie estacionaria, en el cual sus valores varíen mas menos de manera uniforme en cuanto a los valores fijos con respecto al tiempo. Las tendencias aparentes pueden ser ajustadas mediante el uso de la técnica de "diferenciación regular", el cual es un proceso para calcular la diferencia entre dos valores sucesivos, calculando una serie diferenciada la cual posee un comportamiento de tendencia general removido. Si una diferenciación simple no alcanza la estacionalidad, esta podría ser repetida, a pesar de que no ser común, algunas veces se requieren mas de dos diferenciaciones regulares. Si las irregularidades en las series diferenciadas continúan apareciendo, las funciones log o inversa pueden ser especificadas de manera de estabilizar las series, de tal forma que los residuos restantes representen valores cercanos a cero sin ningún patrón de comportamiento. Este es un termino de error equivalente a puro ruido blanco.

Series Aleatorias Puras: Desde otro punto de vista, si las series de datos iniciales no presentan tendencia ni estacionalidad, y los ploteos residuales muestran esencialmente valores cero con un nivel de confianza de 95% sin patrón de comportamiento, quiere decir que no existe problema estadístico real que resolver, lo que implica que vamos en otra dirección. .

Identificación del Modelo de Fondo

Modelo Básico: Con una serie estacionaria como escenario, un modelo básico puede ser identificado ahora. Existen tres modelos básicos, los cuales constituyen las herramientas disponibles: AR (autoregresivo), PM (promedios móviles) y el combinado de ARPM, adicionalmente al especificado anteriormente de DR (diferenciación regular.) Cuando el modelo de diferenciación regular es aplicado en conjunto con AR y PM, son referidos como ARIPM, del cual "I" indica la palabra "integrados" y es la referencia en el procedimiento de diferenciación.

Estacionalidad: En adición a las tendencias, las cuales han sido provistas ahora, las series estacionarias presentan con frecuencia comportamientos estacionales, donde un patrón básico tiende a repetirse a intervalos estacionales regulares. Adicionalmente, el patrón de estacionalidad podría presentar cambios constantes a través del tiempo. Una simple diferenciación fue aplicada a las series de tendencias en general, la diferenciación estacional (DS) se aplica a series estacionales no estáticas. Como las herramientas auto regresivas y de promedios móviles están disponibles para todo tipo de series, también lo están para fenómenos estacionales mediante el uso de parámetros de autoregresiones estacionales (AE), y los parámetros de promedios móviles estacionales (PME).

Estableciendo la Estacionalidad: La necesidad por los parámetros de autoregresiones estacionales (AE) y los parámetros de promedios móviles estacionales (PME) esta establecida mediante la examinación de los patrones de autocorrelación y autocorrelación parcial de una serie estacionaria con retrasos, las cuales son múltiplos de los números de períodos por temporada o estacionalidad. Estos parámetros son requeridos siempre que los períodos de retraso s, 2s, etc, sean diferentes de cero y que presenten patrones asociados con los patrones teóricos asociados a estos modelos. La diferenciación estacional esta indicada si las autocorrelaciones en los periodos de rezago o retraso no decrecen rápidamente.

B-J Modeling Approach to Forecasting?

Acercamiento del Modelo de la Box-Jenkins para Pronósticos
Haga clic en la imagen para ampliarla

En referencia al esquema anterior se sabe que, la varianza de los errores del modelo subyacente deben ser invariantes, es decir, constantes. Esto significa que la varianza para cada subgrupo de los datos es la misma y no dependen del nivel o del punto en el tiempo. Si esta condición es violada, podríamos remediarlo mediante la estabilización de la varianza. Asegúrese de que no existen patrones determinísticos en los datos, de que no existan pulsos o valores inusuales que ocurren una vez, de que no existan cambios de niveles o pasos, y adicionalmente no deberían aparecer pulsos de patrones estacionales.

La razón de todos esto es que si todas estas condiciones existen, la autocorrelación de la muestra y la autocorrelación parcial implicaran una estructura de ARIPM. Adicionalmente, la presencia de este tipo de componentes del modelo pueden esconder estructuras básicas de comportamiento del mismo. Por ejemplo, un simple outlier o pulso pueden crear un efecto donde la estructura se encuentra influenciada por el outlier.

Método de Identificación Cuantitativa Mejorado

Requerimientos para el Análisis Paliativo: Un procedimiento substancialmente mejorado se encuentra disponible en la actualidad para conducir el análisis de la Box-Jenkins ARIPM, el cual apacigua los requerimientos desde una perspectiva de estacionalidad en la evaluación de los patrones ambiguos de autocorrelación y autocorrelación residual para determinar un modelo de Box-Jenkins apropiado para desarrollar un modelo para pronósticos.

ARPM (1, 0): El primer modelo para ser probado en las series estacionarias consiste simplemente en un termino autoregresivo con rezago 1. Los patrones de autocorrelación y autocorrelación parcial son examinados por autocorrelación significante y para ver si los coeficientes residuales se encuentran no correlacionados; esto significa que los coeficientes son cero con limites de confianza de 95% y sin patrones aparentes. Cuando los valores ajustados están lo mas cerca posible a los valores de las series originales, se minimizará la suma de los residuos al cuadrado, lo cual es una técnica llamada la estimación de los mínimos cuadrados. La media residual y el porcentaje de error de la media no deberían ser significantemente diferentes de cero. Algunos modelos alternativos son examinados mediante la comparación del progreso de estos factores, favoreciendo a los modelos que utilizan la menor cantidad de parámetros posibles. La correlación entre los parámetros no debería ser significativamente grande y los límites de confianza no deberían incluir el cero. Cuando se ha establecido un modelo satisfactorio, el procedimiento de pronóstico es aplicado.

ARPM (2, 1): Representa la ausencia de una condición de ARPM (1, 0) satisfactoria con coeficientes residuales aproximándose a cero, el procedimiento de identificación del modelo mejorado examina los patrones residuales cuando los términos autoregresivos con orden 1 y 2 son aplicados junto al término de promedios móviles con un orden de 1.

Procedimiento Subsiguiente: Dependiendo del grado en el cual las condiciones residuales descritas anteriormente no sean satisfechas, el análisis de la Box-Jenkins continúa con un ARPM (n, n-1) hasta que el modelo se satisfaga. En el transcurso de estas iteraciones, cuando un coeficiente autoregresivo (phi) se acerca a cero, el modelo es reexaminado con parámetros ARPM (n-1, n-1). De igual manera, siempre que un coeficiente de promedios móviles (theta) se aproxima a cero, el modelo es reducido a ARPM (n, n-2). En algún punto, ya sea el termino autoregresivo o el termino del promedio móvil podría desaparecer completamente, por lo tanto la examinación de la serie estacionaria se continúa con solo los términos restantes, hasta que los coeficientes residuales se acerquen a cero dentro de los niveles de confianza especificados.

Model Selection in B-J Approach to Forecasting?

Modelo de Selección en el Acertcamiento de Box-Jenkins para Pronósticos
Haga Clic en la imagen para ampliarla

Análisis Estacional: De forma paralela con este ciclo de desarrollo del modelo, y de una forma enteramente similar, los parámetros estacionales autoregresivos y de promedios móviles son agregados y desechados en respuesta a la presencia de los patrones estacionales o cíclicos en los términos residuales o coeficientes acercándose a cero.

Suficiencia del Modelo: En la revisión de los resultados de la Box-Jenkins, se debería tener cuidado en asegurar que los parámetros son significativos y que no están correlacionados, modelos alternados deberían ser ponderados para estas condiciones, así como también para toda la correlación de (R2), error estándar, residuos cero.

Pronosticando con el Modelo: El modelo es usado para pronóstico de corto y mediano plazo, actualizado a medida que los nuevos datos se hacen disponibles de manera de minimizar el número de periodos requeridos con anticipación para el pronóstico.

Monitorear la Precisión del Pronóstico en Tiempo Real: A medida que el tiempo va progresando, la precisión del pronóstico deberá ser monitoreada bastante cerca de manera de observar los incrementos en los términos de error estándar, y disminución en la correlación. Cuando parezca que las series estan cambiando a medida que transcurre el tiempo, se deberían realizar calculaciones de nuevo de los parámetros del modelo.

Modelos Autoregresivos

El modelo autoregresivo es uno del grupo de formulas de predicción lineal que intentan predecir los resultados de un sistema basado en variables de entrada y resultados anteriores, tales como:

Y(t) = b1 + b2Y(t-1) + b3X(t-1) + et,

de donde X(t-1) y Y(t-1) son los valores actuales (valores de entrada) y el pronóstico (resultados), respectivamente. Estos tipos de regresiones son comúnmente referidas entre otros a Modelos Autoregresivos de Rezagos Distribuidos, Rezagos de Distribución Geométrica, y Modelos de Expectativas Adaptativas.

Un modelo que solo depende de resultado previos del sistema es llamado modelo autoregresivo (AR), mientras que un modelo que solo depende de los valores de entrada del sistema es llamado modelo de promedios móviles (PM), y por supuesto, un modelo basado en ambos entradas y salidas del sistema es un modelo autoregresivo de promedios móviles (ARPM). Note que por definición, los modelos AR contienen solo postes (poles) mientras que el PM contiene solo ceros. Para derivar el modelo autoregresivo (AR) se necesita estimar los coeficientes del modelo usando el método del error mínimo.

Los procesos autoregresivos así como su nombre implica, regresan en ellos mismos. Si una observación es hecha en el momento (t), de orden p, [AR(p)], el modelo autoregresivo satisface la siguiente ecuación:

X(t) = F0 + F1X(t-1) + F2X(t-2) + F2X(t-3) + …… + FpX(t-p) + et,

de donde et es una serie de Ruido Blanco.

El valor actual de las series es una combinación lineal de los mas recientes valores pasados de p mas un término de error, el cual incorpora todas las novedades en las series de tiempo en el momento t los cuales no son explicados en los valores pasados. Este es como un modelo de regresión múltiple, pero no es regresado sobre las variables independientes sino en los valores pasados; por lo tanto, el término "Autoregresivo" es utilizado.

Autocorrelación: Una guía importante para las propiedades de las series de tiempo es suministrada por las series de cantidades llamadas coeficientes de autocorrelación muestral o coeficiente de correlación serial, el cual mide la correlación entre observaciones con diferentes distancia de separación entre ellas. Estos coeficientes normalmente proporcionan una sutileza en el modelo de probabilidad que generaron los datos. El coeficiente de autocorrelación muestral es similar al coeficiente de correlación ordinario entre dos variables (x) e (y), excepto por que es aplicado a series de tiempo simples para saber si las observaciones sucesivas están correlacionadas.

Dado un número de observaciones (N) sobre una serie de tiempo discreta, se pueden formar un conjunto de (N - 1) pares de observaciones. Tomando a la primera observación de cada par como una variable, y la segunda observación como la segunda variable, el coeficiente de correlación es llamado coeficiente de autocorrelación de orden uno.

Gráfico de Correlación (Correlograma): Una herramienta útil para interpretar un grupo de coeficientes de autocorrelación es el llamado grafico de correlación o correlograma, el cual es ploteado en contra del rezago (k); donde esta el coeficiente de correlación de rezago (k). Un correlograma puede ser utilizado para obtener una comprensión general de nuestras series de tiempo en los siguientes aspectos:

  1. Una serie aleatoria: Si una serie es completamente aleatoria implica que un número (N) grande será aproximadamente cero para todos los valores de (k) diferentes de cero.

  2. Correlación a corto plazo: Las series estacionarias con frecuencia muestran correlaciones a corto plazo, las cuales están caracterizadas por valores grandes de mas de 2 ó 3 coeficientes de correlación que, mientras son significativamente mas grandes que cero, tienden a ser exitosamente mas pequeños.

  3. Series no estacionarias: Si una serie de tiempo presenta tendencia, los valores de ella no serán cero excepto para valores muy grande de retraso.

  4. Fluctuaciones estacionales: Los modelos autoregresivos comunes con s períodos con fluctuaciones estacionales son:

    X(t) = a + b X(t-s) + et

    y

    X(t) = a + b X(t-s) + c X(t-2s) +et

    donde et es una serie de Ruido Blanco.

Autocorrelación Parcial: Un coeficiente autocorrelación parcial para un orden k, mide la fuerza de la correlación entre los pares de entradas en la serie de tiempo, mientras contabiliza todas las autocorrelaciones (es decir, removiendo los efectos) por debajo del orden k. Por ejemplo, el coeficiente de correlación parcial de orden k = 5 es calculado de tal manera que el efecto de las correlaciones parciales k = 1, 2, 3, y 4 han sido excluidas. El coeficiente de correlación parcial de cualquier orden en particular es el mismo al coeficiente de autoregresión del mismo orden.

Ajustando un Modelo Autoregresivo: Si se piensa que un modelo autoregresivo es apropiado para modelar una serie de tiempo dada, existen dos preguntas relacionadas que necesitan ser contestadas: (1) ¿Cuál es el orden del modelo? y (2) ¿Cómo podemos estimar los parámetros del modelo?

Los parámetros de un modelos autoregresivo pueden ser estimados mediante la minimización de la suma de los residuos al cuadrado con respecto a cada uno de los parámetros, sin embargo, determinar el orden del modelo autoregresivo no es fácil, particularmente cuando el sistema que se intenta modelar tiene interpretaciones biológicas.

Un acercamiento para ajustar los modelos AR de orden progresivamente mayor, es calcular la suma de los residuos al cuadrado para cada valor de p; y luego plotear este resultado en contra de p. Podría ser posible ver el valor de p donde la curva se "aplana", y la adición de parámetros daría una mejoría pequeña al ajuste.

Criterio de Selección: Muchos criterios podrían ser especificados mediante la especificación de un formato dado el correlograma para series de correlación simples o parciales:

  1. Si ninguna de las autocorrelaciones es significativamente diferente de cero, la serie es esencialmente un numero aleatorio o una serie de ruido blanco, la cual no es un modelo autoregresivo manejable.

  2. Si la autocorrelación simple decrece linealmente, pasando por cero hasta convertirse negativa, ó si simplemente la autocorrelación exhibe un patrón cíclico en forma de ola pasando por cero varias veces, la serie no es estacionaria y debe ser diferenciada una o mas veces antes de ser modelada con un proceso autoregresivo.

  3. Si las autocorrelaciones simples exhiben estacionalidad, es decir, existen picos de autocorrelación cada doce periodos (si los datos son mensuales) de rezagos, la serie no es estacionaria, por lo que debe ser diferenciada con una holgura aproximadamente igual a los intervalos estacionales antes de que se adentre en los modelos.

  4. Si la autocorrelación simple decrece de manera exponencial pero se acerca a cero de manera gradual, y mientras las autocorrelaciones parciales son significativamente diferentes de cero a través de números pequeños de rezago mas allá de aquellos que no son significativamente diferentes de cero, la serie debería ser modelado con un proceso autoregresivo.

  5. Si la autocorrelación simple decrece de manera exponencial pero se acerca a cero de manera gradual, y mientras las autocorrelaciones parciales son significativamente diferentes de cero a través de números pequeños de rezago mas allá de aquellos que no son significativamente diferentes de cero, la serie debería ser modelado con un proceso de promedios móviles.

  6. Si la autocorrelación parcial y simple se encuentran por arriba de cero con rezagos sucesivos grandes, pero ninguna de las dos alcanza cero después de cualquier rezago especifico, la serie deberá ser modelada bajo una combinación de los procesos autoregresivo y de promedios móviles.

Las figuras siguientes muestran el comportamiento de autocorrelación y autocorrelación parcial para los modelos AR(1), respectivamente,

De forma similar, para los modelos AR(2), el comportamiento de autocorrelación y autocorrelación parcial son representados a continuación:

Ajustando la Estimación de la Inclinación para la Anchura de las Series de Tiempo: El coeficiente de regresión se basa en modelos autoregresivos obtenidos mediante el Análisis de Regresión de los Mínimos Cuadrados. En el caso de AR(1), la tendencia es -(1 + 3 F1) / n, de donde n es el número de observaciones utilizadas para estimar los parámetros. Obviamente, para grupo de datos grandes estas tendencias son insignificantes.

Condición Estacionaria: Note que un proceso autoregresivo será estable solo si los parámetros se encuentra dentro de un rango específico, por ejemplo, en AR(1), la pendiente debe estar dentro del intervalo abierto (-1, 1). De lo contrario, los efectos pasados estarían acumulados y los valores sucesivos se harían más grandes (o más pequeños); es decir, las series no serian estacionarias. Para ordenes mas grandes, restricciones similares de los valores de los parámetros pueden ser satisfechas.

Condición de Inevitabilidad: Sin la intención de ir a mucho mas detalles, existe una "dualidad" entre una serie de tiempo dada y el modelo de autoregresión que la representa; es decir, la serie de tiempo equivalente puede ser generada por el modelo. Los modelos de AR siempre son invertibles. Sin embargo, de manera análoga al la condición de estacionalidad descrita anteriormente, existen ciertas condiciones para la inversión de los parámetros de PM de la Box-Jenkins.

Pronóstico: Las estimaciones de los parámetros son usadas en el pronóstico para calcular nuevos valores de la serie, mas alla de los incluidos como datos de entrada y los intervalos de confianza para la prediccion de esos valores.

Un Ejemplo Numérico Ilustrativo: El analista de la compañía Aron tiene información de una serie de tiempo sobre las ventas mensuales, las cuales deben ser pronosticadas. Los datos son mostrados a continuación en la siguiente tabla:

Ventas Mensuales de la Compañía Aron (en miles de US$)
t
X(t)
t
X(t)
t
X(t)
t
X(t)
t
X(t)
1
50,8
6
48,1
11
50,8
16
53,1
21
49,7
2
50,3
7
50,1
12
52,8
17
51,6
22
50,3
3
50,2
8
48,7
13
53,0
18
50,8
23
49,9
4
48,7
9
49,2
14
51,8
19
50,6
24
51,8
5
48,5
10
51,1
15
53,6
20
49,7
25
51,0

Mediante la construcción y el estudio de los datos se puede observar que la serie se mueve por arriba y por debajo de la media de 50, 6. Mediante el uso del JavaScript Proceso de Identificación de Series de Tiempo se puede obtener una impresión de que la autocorrelación y autocorrelación simple confirman que la serie de tiempo es estacionaria y que un modelo de autocorrelación de primer orden (p =1) es un buen candidato.

X(t) = F0 + F1X(t-1) + et,

de donde et es una seri de Ruido Blanco.

Condicion de Estacionalidad: El AR(1) es estable si la pendiente se encuentra dentro del intervalo (-1, 1), es decir:

| F1| < 1

es expresada como una hipótesis nula H0 la cual debe ser probada antes de la etapa de pronóstico. Para probar la hipótesis, debemos sustituir la prueba t utilizada en el análisis de regresión para probar la pendiente con la prueba de t introducida por los economistas Dickey y Fuller. Esta prueba es encontrada en el JavaScript Modelando Series de Tiempo Autoregresivas.

El modelo estimado de AR(1) es:

X(t) = 14,44 + 0,715 X(t-1)

Los próximos tres pasos del pronóstico son:

X(26) = 14,44 + 0,715 X(25) = 14,44 + 0,715 (51,0) = 50,91
X(27) = 14,44 + 0,715 X(26) = 14,44 + 0,715 (50,91) = 50,84
X(28) = 14,44 + 0,715 X(27) = 14,44 + 0,715 (50,84) = 50,79

Note: Como siempre es necesario construir el gráfico calcular los estadísticos y comprobar si es estacionaria tanto como en media como en varianza, así como también la prueba estacionalidad. Para varias seruies de tiempo se debería realizar diferenciación, la transformación de los datos y /o desestacionalitización antes de utilizar este JavaScript.

Modelando Series de Tiempo Financieras

Intentamos "modelar" lo que la realidad consiste de modo que podamos predecirlo. El Modelado Estadístico, además de tener la importancia central en la toma de decisiones estadística, es crítico en cualquier esfuerzo, ya que esencialmente todo es un modelo de la realidad. De esta forma, el modelamiento tiene aplicaciones en diferentes campos tales como mercadeo, finanzas, y comportamiento organizativo. En particular, se obliga al modelado de econometría, porque, a diferencia de la mayoría de las disciplinas (como la Economía Normativa), la econometría trata sólo con hechos demostrables, y no con creencia y opiniones.

El análisis de series de tiempo es una parte incorporada del análisis financiero. El tema es interesante y útil, con aplicaciones en la predicción de tasas de intereses, riesgo de divisas, volatilidad de bolsas de valores, y otros por el estilo. Existen muchas variedades de técnicas de multivariación aleatoria y econometría. Algunos ejemplos específicos son la regresión de multivariación aleatoria y la regresión; autoregresiones de vectores; y pruebas de co-integración en modelos de cálculo de valor actual. La siguiente sección presenta la teoría subyacente en la cual los modelos estadísticos enseñados.

Modelos Financieros: Los modelos econométricos son fundamentales en las finanzas y en el análisis de series de tiempo financieras. El modelado es simplemente la creación de representaciones de la realidad. Es importante ser consciente de que a pesar de la importancia del modelo, esto es de hecho sólo una representación de realidad y no la realidad en sí misma. En consecuencia, el modelo debe adaptarse a la realidad; es simplemente vano intentar adaptar la realidad al modelo. Como simples representaciones, los modelos no pueden ser exactos. Los modelos implican que la acción es tomada sólo después del razonamiento y la cuidadosa reflexión. Esto podría tener consecuencias principalmente en el reino de las finanzas. Un elemento clave para planificación financiera y el pronóstico financiero es la capacidad de construir modelos mostrando los datos financieros interrelacionados. Los modelos mostrando correlación o causalidad entre variables pueden ser usados para mejorar la toma de decisiones financiera. Por ejemplo, se estaría más preocupado por las consecuencias en la bolsa de valores doméstica de un descenso en algún otra economía foránea, si puede ser mostrado que existe un impacto matemáticamente demostrable de los efectos causados por la economía externa en la bolsa de valores doméstica. Sin embargo, el modelado esta lleno de peligros. Un modelo que antes era vigente puede perder la validez debido a cambios en las condiciones, haciendo una representación inexacta de la realidad y afectando negativamente la capacidad de los gerentes para tomar la mejor decisión disponible.

Los ejemplos de variantes aleatorias y de regresiones aleatorias multivariantes, autoregresión de vector, y la co-integración del valor actual ilustran algunas de las aplicaciones del modelado, lo cual es una dimensión vital en la toma de decisiones gerenciales, en la econometría, y expresamente en el estudio de series de tiempo financieras. La naturaleza demostrable de modelos econométricos es impresionante; más que ofrecer soluciones a problemas financieros basados en intuición o convención, se podría demostrar matemáticamente si un modelo es o no es válido, o si requiere alguna modificación. Adicionalmente, puede ser observado que el modelamiento es un proceso iterativo, dado que los modelos deben cambiar continuamente para reflejar la realidad la cual no es constante. La capacidad de realizar estas tareas tiene ramificaciones asombrosas en el reino financiero, donde la posibilidad de los modelos para predecir exactamente serie de tiempo financiera está directamente relacionada con la capacidad del individuo o firma para obtener beneficios en diferentes escenarios financieros.

Modelos Univariantes y Multivariantes: El uso del análisis de regresión es ampliamente utilizado en la examinación de series de tiempo financieras. Entre algunos ejemplos se encuentran el uso de las tasas de variación de monedas extranjeras como pronosticadores óptimos para las tasas de referencia; la varianza condicional y la prima de riesgo en los mercados cambiarios extranjeros; y las tasas de retorno y volatilidad de las acciones bursátiles. Un modelo que ha sido utilizado de manera exitosa en este tipo de aplicaciones es el llamado modelo GARCH-M, el cual incorpora los cálculos de la media dentro del modelo GARCH (autoregressive conditional heteroskedastic = condicional autoregresivo generalizado de Heterocedasticidad.) Quizás esta definición suene compleja y esotérica, pero esto simplemente significa que los errores de series correlacionados y la varianza condicional introducen el cálculo de la media, y que la varianza condicional en si misma depende del vector de variables explicativas. El modelo GARCH-M ha sido modificado en muchas oportunidades en las pruebas realizadas por los practicantes de las finanzas debido a la necesidad de adaptarlo a los cambios de la realidad. Por ejemplo, ahora este modelo puede manejar funciones exponenciales (no lineales), además de que ya no esta limitado a tratar con parámetros no negativos solamente.

Una de las aplicaciones de este modelo es el análisis de las tasas de retorno y volatilidad de las acciones bursátiles. Tradicionalmente se cree que la varianza en el retorno de inversión es la primera medida de riesgo para los inversionistas. Sin embargo, usando datos extensos de serie de tiempo, se ha comprobado que la relación entre los retornos de la media y los retornos de la varianza o desviación estándar es débil; de aquí se deriva que los modelos de dos parámetros para la estimación de precios no son apropiados, y las pruebas matemáticas sustituyen esta aseveración. Dado que las decisiones presupuestas en los modelos originales son necesariamente sub óptimas porque la premisa original es desechada, es ventajoso para la gente de finanzas abandonar el modelo por uno que tenga una representación más exacta de la realidad.

La especificación correcta del modelo es de importancia suprema, para ello se han desarrollado un conjunto de pruebas para los criterios que determinan la errónea especificación del mismo. Estas incluyen la prueba de normalidad, linealidad y homocedasticidad, las cuales pueden ser aplicadas en una gran variedad de modelos. Un ejemplo simple, el cual arroja resultados sorprendentes en el Modelo de Precios de Activos de Capital (MPAC) y es uno de las bases de la economía, es la aplicación de criterios de evaluación de datos concernientes a la prima de riesgo de compañías que muestran evidencia significativa de no-linealidad, no-normalidad y parámetros no constantes. Se encontró que el MPAC podía ser aplicable solamente en tres de las diecisiete compañías que fueron analizadas. Sin embargo esto no significa que el MPAC debe ser rechazado repetidamente, el mismo tiene un gran valor como herramienta pedagógica. Para los econometristas y profesionales de finanzas, para los cuales la falta de especificación del modelo puede conllevar a decisiones financieras sub óptimas, el modelo MPAC debe ser sustituido por uno mejor, específicamente uno que muestre la la naturaleza de la variación temporal de los betas. El marco de los modelos GARCH-M es uno de ellos.

Los modelos de regresión de multivariación aplican al mismo marco conceptual. La diferencia principal es que se reemplaza una variable dependiente por un vector. La teoría de estimación es esencialmente una extensión de la de multivariación desarrollada por el de univariación, tal que puede ser utilizado para evaluar modelos de volatilidad de acciones bursátiles y de CAPM. En el caso de CAPM, el vector introducido es el exceso en el retorno de activos a un momento designado. Una aplicación es el cálculo del CAPM con covarianzas cambiantes a través del tiempo. A pesar de que en este ejemplo la hipótesis nula de que todas las interceptaciones son cero no puede ser rechazada, los problemas de ausencia de especificación del modelo de invariación todavía permanecen. La estimación de la pendiente y la interceptación también permanecen igual dado que la misma regresión aparece en cada ecuación.

Vector de Autoregresión: Los modelos generales de regresión asumen que la variable dependiente es una función sus mismos valores pasados, y de los valores pasados y presentes de la variable independiente. Por los tanto, la variable independiente es débilmente exógena dado que contiene una estructura estocástica que no suministra información para la estimación de los parámetros de interés. Mientras que la debilidad de ser exógena permita estimaciones eficientes de los parámetros de interés sin ninguna referencia de su propia estructura estocástica, problemas en la predicción de las variables dependientes podrían incrementar si la "reacción" de las variables dependientes a las independientes se desarrolla a través del tiempo. (Cuando no existe este tipo de reacciones, se dice que la variable dependiente no causa Granger en la variable independiente.) Una exogenidad débil acompañada de no-causalidad de Granger genera fuerte exogenidad, el cual, a diferencia de la exogenidad débil, es directamente evaluable. Para realizar las pruebas requeridas para la utilización del Modelo de Ecuación Dinámica Estructural (MEDE) y el Proceso de Vector Autoregresivo (VAR). Por lo tanto el modelo de regresión multivariante es extendido en dos direcciones, permitiendo simultaneidad entre las variables exógenas y las variables dependientes, y explícitamente considerando el proceso de generación de variables independientes exógenas

Los resultados de estas pruebas son útiles en la determinación de si una variable independiente es estrictamente exógena o predeterminada. La exogenidad estricta puede ser evaluada en el MEDE expresando cada variable endógena como un rezago distribuido infinitamente de la variable exógena. Si la variable independiente es estrictamente exógena, la atención se puede limitar a la distribución condicional de las variables independientes sin perdida de información, resultando en una simplificación de la inferencia estadística. Si la variable independiente es exógena y además predeterminada, significa que todos sus valores pasados y actuales son independientes de los términos actuales de error. Mientras que la exogenidad estricta se encuentra bastante relacionada al concepto de no-causalidad, los dos conceptos no son equivalentes, ni son intercambiables.

Algo puede ser observado de este tipo de análisis y es que es útil en la verificación de que un modelo es apropiado así como también para probar que, en algunos casos, el proceso de inferencia estadística puede ser simplificado sin sacrificar precisión, por consiguiente tanto la fortaleza como la credibilidad del modelo incrementa la eficiencia del proceso de modelamiento. Los vectores de autoregresión pueden ser utilizados para calcular otras variaciones de causalidad, incluyendo causalidad instantánea, dependencia lineal, y medición de reacción desde las variables dependientes a las independientes y viceversa. Es posible avanzar a otros procedimientos con las pruebas de causalidad, pero estudios de simulación ya realizados, han alcanzado el consenso de que la combinación mas eficiente entre confiabilidad y facilidad puede ser obtenida mediante el procedimiento descrito anteriormente.

Modelamiento de Co-Integración y Valor Presente: Los modelos de valor presente son extensamente utilizados en finanzas para formular modelos de eficiencia en los mercados. En términos generales, un modelo de valor presente para dos variables y1 y x1, establece que y1 es una función lineal del valor presente descontado del valor futuro esperado de x1, de donde el termino constante, el factor de descuento constante, y el coeficiente de proporcionalidad son conocidos o necesitan ser estimados. No todas las series de tiempo financieras son no-integradas; la presencia de variables integradas afecta los resultados de la regresión estándar y los procesos de inferencia. Adicionalmente las variables podrían estar co-integradas, lo que implica la súper imposición de vectores de co-integración en el modelo, y resultando en circunstancias bajo las cuales el concepto de equilibrio pierde todas las implicaciones prácticas, por lo que podrían ocurrir regresiones falsas. En el análisis de valor presente, la co-integración puede ser utilizada para definir la "extensión teórica" y para identificar los movimientos comunes entre variables. Es bastante útil en la construcción de la pruebas basadas en volatilidad.

Una prueba de referencia es la volatilidad de los mercados bursátiles. Asumiendo la co-integración, se construyen los vectores autoregresivos de segundo orden, los cuales sugieren que los cambios en dividendos no son fácilmente predecibles, pero son Granger-causados por la extensión. Cuando el valor de la tasa de descuento asumida es incrementado, algunas restricciones pueden ser rechazadas a un bajo nivel de significancia. Este resultado muestra un "exceso de volatilidad" mucho mas pronunciado que el obtenido en el modelo de valor presente. Adicionalmente, muestra que el modelo es mas apropiado en situaciones donde la tasa de descuento es mas alta. Las implicaciones de utilizar un acercamiento de co-integración a las pruebas de volatilidad de los mercados bursátiles son significativas para los gerentes de finanzas. De una significancia relacionada proviene la habilidad de probar las hipótesis de expectativas de los términos estructurales de las tasas de interés.

El error medio absoluto es una fuerte medida de error. Sin embargo, se podría utilizar la suma de los errores para comparar el éxito de cada modelo de pronóstico en relación a la línea de fondo, tal como un modelo de camino aleatorio, el cual normalmente utiliza modelos financieros de series de tiempo.

Econometría y Modelos de Series de Tiempo

Los modelos econométricos están compuestos por modelos de regresiones simultáneas con aplicaciones a áreas tales como Economía Industrial, Agricultura, Regulaciones y estrategia Corporativas. Los modelos de series de tiempo requieren un numero grabnde de observaciones (mas de 50.) Ambos modelos han sido utilizados de manera exitosa en aplicaciones de negocios, abarcando un rango que va desde micro hasta macro estudios, incluyendo finanzas y crecimiento endógeno. Entre otros acercamientos al modelamiento se encuentran los modelos estructurales y clásicos como el acercamiento de la Box-Jenkins, el análisis de co- integración, y los modelos probabilísticos generales de micro econometría; como el Logit, y Probit, panel de datos secciones cruzadas. Los modelos econométricos estudian los asuntos relacionados a la causalidad; por ejemplo, identificando la relación causal entre un resultado y el grupo de factores que podrían haber generado ese resultado. En particular, esto hace este concepto operacional en series de tiempo y en modelos exógenos

Ecuaciones Simultaneas

La especificación empírica típica en economía o finanzas es un modelo de una sola ecuación el cual asume que las variables explicativas no son estocásticas e independientes del termino de error.

Esto permite al modelo ser estimado por el análisis de Regresión de Mínimos Cuadradas (RMC) este tipo de modelos no dejan dudas de la dirección de causa asumida, es decir, corre directamente desde las variables explicativas hacia las variables dependientes de la ecuación.

El análisis de RMC esta destinado a ajustar una ecuación simple de regresión. En la práctica, la mayoría de las relaciones económicas interactúan entre sistemas de ecuaciones simultaneas, y cuando es te es el caso, la aplicación de del RMC a una simple relación aislada, conlleva a estimaciones influenciadas. Por lo tanto, es importante mostrar como es posible utilizar el RMC para obtener estimaciones consistentes de los coeficientes de una relación.

La estructura general de un modelo de ecuaciones simultaneas consiste en una serie de ecuaciones independientes con variables endógenas y exógenas. Las variables endógenas son determinadas dentro del sistema de ecuaciones. Las variables exógenas o como se conocen generalmente, las variables pre-determinadas, ayudan a describir el movimiento de las variables endógenas dentro del sistema, o son determinadas fueras del modelo.

Aplicaciones: Sistemas de ecuaciones simultaneas constituyen un tipo de modelos donde algunas de las variables económicas son determinadas conjuntamente. El ejemplo típico en los textos de econometría es el modelo de oferta y demanda de bienes y servicios. La interacción entre la oferta y la demanda presiona al modelos a determinar de manera conjunta el precio y cantidad de producto de equilibrio dentro del mercado. Debido a la correlación potencial existente entre las variables del lado derecho de las ecuación que incluye el termino de error, no tiene sentido continuar hablando sobre variables dependientes e independientes. Por lo tanto, hacemos la distinción entre variables endógenas y exógenas.

La estimación de ecuaciones simultaneas no se limita al modelo de oferta y demanda. Existen muchas mas aplicaciones tales como el modelo de gasto es consumo, el impacto de presiones proteccionistas en los modelos de cambio y tasa de interés. Los modelos de ecuaciones simultaneas tienen aplicaciones naturales en la literatura de la banca y finanzas debido a la determinación conjunta del riesgo, retornos en inversión y la relación de transformación entre los depósitos y los activos bancarios.

Ecuaciones Estructurales y de Forma Reducida: Considere el siguiente modelo Keynesiano para la determinación del ingreso agregado basado en una función de consumo y una identidad de ingreso:

C = b1 + b2Y + e
Y = C + I,

Donde:

C es el gasto en consumo agregado en el período de tiempo t,
I es la inversión agregada en el período t,
Y es el ingreso agregad en el periodo t, y
e es el término de turbulencia (error) con media cero y varianza constante.

Estas ecuaciones son llamadas Ecuaciones Estructurales las cuales proporcionan una estructura de cómo la economía funciona. La primera ecuación es la de consumo la cual relaciona el gasto con el ingreso. El coeficiente b2 es la propensión marginal a consumir, la cual es verdaderamente útil si podemos estimarla. Para este modelo, C e Y son las variables endógenas. El resto de las variables son llamadas exógenas, tales como la inversión I. Note que deben existir tantas ecuaciones como variables endógenas.

Ecuaciones de Forma Reducida: Dada la condición de que I es exógena, se deriva la ecuación forma reducida para C e Y.

Sustituyendo por Y en la primera ecuación,

C = b1 + b2 (C + I) + e.

Por lo tanto,

C = b1 / (1 - b2) + b2 I / (1 - b2) + e / (1 - b2),

y

Y = b1 / (1 - b2) + I / (1 - b2) + e / (1 - b2),

Ahora podemos utilizar el análisis de RMC para estimar esta ecuación. Esto es totalmente permisible porque la inversión y el término de error no están correlacionados dado el hecho de que la inversión es exógena. Sin embargo, utilizando la primera ecuacion se puede obtener una pendiente estimada b2 /(1 - b2), mientras que la segunda ecuación proporciona otra estimación de 1 /(1 - b2). Por lo tanto, tomando los ratios de estas formas reducidas, las pendientes proporcionaran una estimación de para b.

Una Aplicación: la tabla siguiente proporciona los datos de consumo de capital, e ingreso doméstico en US$ para 33 paises en el año 1999.

País
C
I
Y
País
C
I
Y
Australia
15024
4749
19461
Corea del Sur
4596
1448
6829
Austria
19813
6787
26104
Luxemburgo
26400
9767
42650
Bélgica
18367
5174
24522
Malasia
1683
873
3268
Canada
15786
4017
20085
Mexico
3359
1056
4328
China
446
293
768
Holanda
17558
4865
24086
China-HK
17067
7262
24452
Nueva Zelanda
11236
2658
13992
Dinamarca
25199
6947
32769
Noruega
23415
9221
32933
Finlandia
17991
4741
24952
Pakistán
389
79
463
Francia
19178
4622
24587
Filipinas
760
176
868
Alemania
20058
5716
26219
Portugal
8579
2644
9976
Grecia
9991
2460
11551
España
11255
3415
14052
Islandia
25294
6706
30622
Suecia
20687
4487
26866
India
291
84
385
Suiza
27648
7815
36864
Indonesia
351
216
613
Tailandia
1226
479
1997
Irlanda
13045
4791
20132
Reino Unido
19743
4316
23844
Italia
16134
4075
20580
EEUU
26387
6540
32377
Japón
21478
7923
30124
       

Mediante la implementación del JavaScript de Análisis de Regresión, dos veces, una para (C e I), y la otra para (Y e I), el coeficiente estimado b2 obtenemos que la propensión marginal es 0,724.

Intervalo de Predicción para una Variable Aleatoria

In muchas aplicaciones de la estadística para negocios, tales como los pronósticos, se esta interesado en la construcción de intervalos estadísticos para variables aleatorias en vez de un parámetro de una distribución poblacional. Por ejemplo, digamos que X es una variable aleatoria con distribución normal, con una media estimada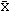 y desviación estándar S, por lo tanto el intervalo para la media muestral 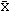con nivel de confianza de 100(1- a)% es:

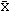- t . S (1 + 1/n)   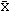 ,     + t . S (1 + 1/n)

Este es el rango para una variable aleatoria 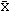con 100(1- a)% de confianza, utilizando la tabla t. Descansando en la condición de normalidad para la predicción de la media muestral, se requiere que el tamaño de la muestra n sea mayor a 30.

Método de II Censo de Análisis de Estacionalidad

 El II Censo es una variante de X-11. El procedimiento X11 proporciona ajustes estacionales en series de tiempo utilizando el Censo X-11 el método ARIPM X-11. El procedimiento X11 se basa en el programa de ajuste de la Oficina de Censo de los EEUU X-11 (US Bureau of the Census), y también respalda el método ARIPM X-11 desarrollado por Canadá Estadísticas (Statistics Canada.)

Mediciones para la Exactitud

 El método mas sencillo para evaluar la exactitud de un pronóstico es plotear los valores observados y el pronóstico de un periodo adelantado en la identificación de comportamientos residuales a través del tiempo.

Las medidas estadísticas de error mas utilizadas, las cuales pueden ayudar a identificar un método o valores óptimos de los parámetros dentro de un método son:

Error Medio Absoluto: El valor del error absoluto medio (EAM) es el valor average del error absoluto. Mientras este valor se encuentre mas cerca de cero, mejor será el pronóstico.

Error Medio al Cuadrado (EMC): Es la suma (o average) de los valores de errores al cuadrado. Este es el indicador de ausencia de ajuste mas utilizado en los procedimientos de ajuste estadístico. Esta medida es muy sensitiva a cualquier outlier en comparado con el error medio absoluto; esto es, valores atípicos grandes tendrán un impacto importante en el valor de EMC.

Error Absoluto de Porcentaje Relativo (EAPR): Esta medida descansa en el valor de error sin considerar las magnitudes de los valores observados. El EAPR es calculado como el promedio de los valores de APE:

Error Absoluto de Porcentaje Relativo t = 100|(Xt - Ft )/Xt|%

El Estadístico de Durbin-Watson cuantifica la correlación serial de los errores en el análisis y pronóstico de las series de tiempo. El estadístico D-W esta definido por:

Estadístico D-W = S2n (ej - ej-1)2 / S1n ej2,

de donde ej es el j-ésimo error. D-W toma valores entre [0, 4]. Para correlaciones no en serie, es esperado un valor cercano a 2. Con una correlación serial positiva, las desviaciones adyacentes tienden a tener el mismo signo; por lo tanto el D-W se transforma a menor que 2; sin embargo con una cortrelacion serial negativa, alternando los signos de error, el D-W toma valores mayores a 2. Para pronósticos donde el valor de D-W es significativamente diferente de 2, las estimaciones de la varianza y la covarianza de los parámetros del modelo pueden estar en error, podrían ser o muy grandes o muy pequeños.

En la medición de la precisión del pronóstico se debería determinar primero la función de pérdida y de allí, una medida conveniente de precisión. Por ejemplo, la función cuadrática de pérdida implica el uso del EMC. Por lo general tenemos muy pocos modelos para hacer comparaciones, por lo que tratamos de escoger el "mejor". Por lo tanto se debe tener mucho cuidado al estandarizar los datos y los resultados de manera de que un modelo de varianza grande no 'ensucie' el otro modelo.

Una Aplicación: La tabla siguiente muestra un conjunto de datos con algunas medidas de precisión:

Períodos Observaciones Predicciones
1 567 597
2 620 630
3 700 700
4 720 715
5 735 725
6 819 820
7 819 820
8 830 831
9 840 840
10 999 850
Algunas Medidas de Precisión Comúnmente Usadas
Error Absoluto Medio 20,7
Error Relativo Medio(%) 2,02
Desviación de los Errores Estándar 50,91278
Estadístico de Theils 0,80
Estadístico de Mc Laughlins 320,14
Estadístico de Durbin-Watson 0,9976

A usted podría gustarle comprobar sus cálculos utilizando el JavaScript Midiendo la Precisión, y luego realizar algunas experimentaciones numéricas para una compresión mas profunda de estos conceptos.

El Mejor Momento para Reemplazar Equipos

La actividad o funcionamiento de casi todo desciende con los años. Un ejemplo, las maquinarias. A pesar de que el mantenimiento rutinario puede mantener los equipos trabajando eficientemente, llega un momento en el cual el costo de reparación es muy elevado, y es menos costoso comprar un reemplazo.

Ejemplo Numérico: La tabla siguiente muestra el costo de reemplazar una maquinaria con valor de $100000, el valor esperado de re-venta, junto a los costos por cada año (en miles de US$).

Datos para la Decidir el Año de Reemplazo de un Equipo
Antigüedad de la Maquinaria
0
1
2
3
4
5
Valor de Re-venta
100
50
30
15
10
5
Costos Corrientes
0
5
9
15
41
60

 

El gerente debe decidir cual es el mejor momento para reemplazar la maquinaria. Los aspectos computacionales se encuentran ordenados en la tabla siguiente:

Aspectos Computacionales y de Análisis
Antigüedad de la Maquinaria
1
2
3
4
5
Costos Corrientes Acumulados
5
14
29
70
130
Costos de Capital ($100 costo de re-venta)
50
70
85
90
95
Costo Total con respecto a la Antigüedad
55
84
114
160
225
Costo Promedio con respecto a la Antigüedad
55
42
38
40
45

El análisis de ploteo del costo promedio con respecto a la antigüedad indica que tiene una forma de parábola tal y como se con un costo mínimo anual de $38000. Esto corresponde a la decisión de reemplazar la maquinaria al final del tercer año.

Representación Matemática: Podemos construir un modelo matemático para el costo promedio como función de la antigüedad..

Sabemos que queremos una función cuadrática la cual proporciona es la mas ajustable, podríamos utilizar el JavaScript de la Regresión Cuadrática para estimar sus coeficientes. El resultado es:

Costo promedio con respecto al tiempo = 3000(Año)2 -20200(Año) + 71600,        para 1 £ Año £ 5.

Su derivada es: 6000(Año) - 20200 la cual, desaparece al año = 101/30. Esto implica que el mejor año o momento para reemplazar la maquinaria es al tercer año con 4,4 meses.

A usted podría gustarle utilizar el JavaScript de Periodo Optimo para Reemplazar para comprobar sus cálculos y realizar algunas experimentaciones para una comprensión mas profunda.

Análisis de Pareto: El ABC para la Clasificación de Inventarios

Vilfredo Pareto fue un economista italiano que notó que 80% de la riqueza estaba poseída por solo el 20% de la población. El análisis de Pareto ayuda a elegir cual es el cambio más efectivo para hacer. El uso del principio paretiano se ejemplifica en el hecho de que haciendo solo el 20% del trabajo genera las ventajas del 80% de su totalidad. El análisis de Pareto es una técnica formal para encontrar los cambios en inventarios que generaran los beneficios más altos. Este análisis es muy útil donde existen muchos caminos de acción compitiendo para ser seleccionados. Para comenzar el análisis, escriba una lista de cambios de inventarios que se podrían realizar. Si se tiene una lista larga, agrúpelas en cambios relacionados entre sí, luego ubíquelas de acuerdo al orden de importancia. El primer cambio que se mezcla o realiza es el que tiene el mas alto resultado o importancia, el cual proporcionará el mayor beneficio en el caso de ser resuelto. Las opciones con los resultados más bajos probablemente no tendrán ningún valor el resolverlas porque quizás podrían costar más las soluciones que su mismo valor.

Aplicaciones del ABC para la Clasificación de Inventarios: El objetivo es clasificar los inventarios con cierta medida de importancia y asignar los esfuerzos de control respectivos. Un aspecto importante de este sistema de control de inventarios es el grado de necesidad de monitoreo. Los volúmenes de demanda y los valores unitarios varían; por lo tanto, los inventarios pueden ser clasificados de acuerdo su valor para determinar cuanto control es aplicado.

El proceso de clasificación es como sigue a continuación: Determinar el uso anual en dólares para cada artículo; es decir, la demanda anual por el costo de cada artículo, y luego ordenarlos en orden decreciente. Calcule el uso total n dólares. Calcule el porcentaje (%) de dólares usados en cada artículo. Ordene los artículos en tres clases de acuerdo al porcentaje en dólares utilizados:
A = Muy Importante, B = Moderadamente Importante, y C = Menos Importante.

Ejemplo Numérico: Considere una pequeña tienda que tiene nueve tipos de productos con los siguientes costos y niveles de demanda anual:

Nombre del Producto
P1
P2
P3
P4
P5
P6
P7
P8
P9
Costo ($100)
24
25
30
4
6
10
15
20
22
Demanda Anual
3
2
2
8
7
30
20
6
4

Calcule el uso anual de cada producto en términos de dólares, y luego ubique los valores numéricos en orden decreciente, así como es mostrado en la tabla siguiente. El uso anual total de acuerdo a sus respectivos valores es 1064.

Uso Anual por Valor
300
300
120
88
72
60
50
42
32
Nombre del Producto
P6
P7
P8
P9
P1
P3
P2
P5
P4
% de Uso Anual
28
28
11
8
7
6
5
4
3
Categoría
A
B
C

Trabajando de arriba hacia debajo de la tabla, se determina el porcentaje de (%) de dólares gastados en cada artículo. Esta fila describe el comportamiento de la función de distribución acumulativa, donde se determina el cambio de una categoría a la siguiente. Seleccione los artículos en tres categorías de acuerdo al porcentaje de gastos en dólares: A= Muy importante, B= Moderadamente importante y, C= Menos importante.

El JavaScript del ABC para la Clasificación de Inventarios construye una función de distribución empírica acumulativa (FDEA) como una herramienta de medición y como un proceso de decisión del ABC para la clasificación de inventarios. La figura siguiente representa la clasificación basada en la FDEA del ejemplo numérico:

A pesar de toda esta información, la determinación de los límites entre las categorías de los artículos o productos es con frecuencia subjetiva. Para nuestro ejemplo, los artículos en la Clase A requieren controles de inventario bien rigurosos, el cual es mejor para pronósticos más exactos, mejor control de registros, y menor nivel de inventarios mientras que los artículos en la Clase C tienden a tener menos control.

A usted podría gustarle utilizar el JavaScript del ABC para la Clasificación de Inventarios para comprobar sus cálculos manuales.

Análisis de Costo/ Beneficio: La Cantidad Económica

El análisis de costo beneficio es un proceso para encontrar buenas respuestas a las preguntas siguientes: Dada una evaluación de costos y beneficios realizada por un gerente, ¿Cuál seria la opción recomendada? El análisis de costo beneficio envuelve los siguientes pasos generales: Especificar una lista de todos los cursos de acción posibles. Asignar un valor (positivo o negativo) para los resultados de cada acción a tomar, y calcular la probabilidad de cada resultado. Calcular el resultado esperado para cada acción o procedimiento. Tomar el procedimiento que proporcione el mejor resultado esperado.

Aplicación de la Determinación de la Cantidad Económica: El análisis de costo beneficio es normalmente utilizado en economía para las estrategias óptimas de producción. Los costos son la preocupación principal porque cada unidad adicional que se agrega al total incrementa los mismos. Luego de comenzar la producción y por lo tanto los costos asociados, El costo marginal de producir una unidad adicional es constante o incrementa en proporción al incremento de las unidades producidas. Cada unidad de producto adicional tiende a costar tanto o mas que la unidad anterior. En cierto punto, el costo adicional de una unidad extra de producto sobrepasará los beneficios adicionales.

La mejor estrategia puede ser encontrada mediante el uso de un diagrama, mediante el cual de plotean los valores de costos y beneficios en el eje horizontal y eligiendo el punto donde la distancia entre ambos es mayor, así como es mostrado en la figura siguiente:

Alternativamente, se podría plotear el beneficio neto y encontrar la cantidad optima donde este es máximo, así como es representado en la siguiente figura:

Finalmente, se podrían plotear las curvas de beneficio marginal y costo marginal y escoger el punto donde se interceptan, así como se muestra en la figura siguiente:

Note que, porque las "ganancias netas" están definidas como (beneficios - costos), en el punto máximo su derivada desaparece; por lo tanto, la pendiente de las ganancias máximas es cero en el punto de cantidades de producción optimas. Para determinar la distancia máxima entre dos curvas, se enfoca en el cambio incremental o marginal de una curva en relación con la otra. Si el beneficio marginal de producir una unidad adicional es mayor a su costo marginal, producir mas es una buena estrategia. Si el beneficio marginal de producir una unidad adicional es menor que su costo marginal, producir no seria una buena estrategia. En el punto máximo, el beneficio adicional simplemente compensara el costo marginal; por lo tanto, no existe cambio en las ganancias netas, es decir, la cantidad optimas es donde el

Beneficio marginal = Costo marginal

A usted podría gustarle utilizar el JavaScript de Regresión Cuadrática para estimar las funciones de costo y beneficio basadas en un conjunto de datos dados.

Herramientas de Modelamiento para el Control de Inventarios

Controles de inventarios esta referido a la minimización de los costos totales en inventarios. En el Reino Unido este término es también llamado control de stock o almacén. Los tres factores principales en el proceso de toma de decisiones en el control de inventarios son:

El tercer elemento es el mas difícil de medir y es normalmente manejado por el establecimiento de pólizas de "niveles de servicio"; es decir, cierto porcentaje de la demanda será cubierta sin retardo.

Decisiones sobre el control de inventarios es tanto un problema como una oportunidad para por lo menos tres departamentos diferentes tales como Producción, Mercadeo y Contabilidad. La toma de decisiones en el control de inventarios tiene un impacto enorme en la productividad y desenvolvimiento de muchas organizaciones porque este maneja el flujo total de materiales. El control de inventarios apropiado puede minimizar desabastecimiento de materiales, por lo tanto reducir el capital de una organización. Adicionalmente posibilita a una organización a comprar o producir un producto en cantidades mas económicas, por lo tanto minimizar el costo general de producción.

Los inventarios son tanto bienes sin uso en un depósito, materias prima para ser utilizadas, materiales en proceso, bienes finales, como individuos. Un buen modelo de inventarios nos permite:

Para cada modelo de inventario, el tomador de decisiones esta preocupado de la pregunta principal: ¿Cuando debe ser realizado el reemplazo de una orden? Se deben revisar los niveles de stock a intervalos fijos o reordenar cuando el stock cae a un nivel predeterminado; es decir, al nivel de seguridad de stock fijo.

 

Palabras Claves, Notaciones Comúnmente Utilizadas en el Modelamiento y Herramientas de Análisis para el Control de Inventarios
Tasa o Nivel de Demanda: x Una tasa constante al cual los productos son retirados del inventario
Costos de orden: C1 Este es el costo fijo de colocar una orden independiente del monto ordenado.
Costos de preparación
Costos de manutención : C2 Este costo usualmente incluye la perdida de ingresos por inversión causados por la manutención del activo atado al inventario (no circulación del mismo). Esto ni es un flujo real de efectivo, pero es un componente importante del costo de inventarios. Si P es el precio por unidad de producto, este componente es normalmente calculado por iP, donde i es un porcentaje que incluye el costo de oportunidad, el costo de ubicación, seguro, etc. Este es una tasa de descuento o una tasa de interés utilizada para calcular el costo de mantener unidades de inventario en los almacenes.
Costos de Desabastecimiento: C3 Debe existir un costo para cuando la escasez ocurre.
Costo de Respaldo de ordenes: C4 Este costo incluye los gastos por cada articulo respaldado. Esto podría ser un gasto para cada articulo en proporción l tiempo que cada cliente debe esperar por dicho producto.
Tiempo de reemplazo: L Es el intervalo de tiempo que transcurre mientras una orden es hecha y el inventario es reemplazado.

Los modelos probabilísticos y determinísticos mas utilizados son mostrados en la sección siguiente:

El Modelo Clásico OEC: Este es el modelo mas simple construido basándose en el principio de que los bienes obtenidos el mismo día que son ordenados sin permitir escasez. Claramente, se debe ordenar nuevamente cuando el inventario alcanza 0, o considerando el tiempo de reemplazo L

La figura siguiente muestra los cambios en los niveles inventarios con respecto al tiempo:

La figura muestra el tiempo en el eje de las x y el nivel de inventario en el eje de las y. Se comienza en el tiempo cero cuando una orden llega. La cantidad de la orden es el tamaño del lote, Q. El lote completo es enviado al mismo momento por lo que el inventario se dispara instantáneamente desde 0 hasta Q. Los materiales son sustraídos del inventario a una tasa de demanda constante, x, medida en unidades por tiempo. Luego que el inventario es mermado, el tiempo para el arribo de otra orden de tamaño Q llega, y el ciclo se repite de nuevo.

El patrón de inventario mostrado en la figura anterior, es obviamente una abstracción de la realidad porque no se espera que un sistema real opere exactamente como mostramos. La abstracción proporciona una estimación del tamaño de lote óptimo, llamado orden económico de cantidad (OEC), y cantidades relacionadas. Consideraremos posiciones alternativas a esta definición mas adelante.

 
Ordenes
  
Almacenamiento
Costo Total=
C1x/Q
 +
C2/(2Q)

La Cantidad Optima de Ordenes = Q* = (2xC1/C2) 1/2, por lo tanto,
el Ciclo Optimo de Re-ordenamiento = T* = [2C1/(xC2)]1/2

Ejemplo Numérico 1: Suponga que su oficina utiliza 1200 cajas al año de papel para maquinas de escribir. Usted debe determinar la cantidad que debe ser ordenada, y con que frecuencia se debe hacer. Los datos a considerar son la tasa de demanda x= 1200 cajas al año, el costo de ordenamiento C1 = $5 por orden, costos de manutención o mantenimiento C2 = $1.20 por caja, por año.

La cantidad óptima de ordenamiento es Q* = 100 cajas, esto nos proporciona el número de ordenes = 1200/100 = 12, es decir, 12 ordenes por año, o una vez por mes.

Note que se debe incorporar el tiempo de reemplazo (L), el cual es el intervalo de tiempo que transcurre desde que una orden es hecha hasta que es repuesto.

Modelos con Escasez: Cuando un cliente busca un producto y encuentra el inventario vacío, la demanda puede ser satisfecha cuando el producto se haga disponible. Normalmente, clientes reciben descuentos que son incluidos en los costos de ordenes de respaldo.

Un modelo con ordenes de respaldo es mostrado en la figura siguiente:

En este modelo, la escasez de productos es permitida por un periodo de tiempo antes de ser reemplazados los productos. En referencia a la respuesta de los clientes por la falta de disponibilidad de productos, los mismos aceptaran entregas retrasadas lo cual es llamado orden de respaldo. Existen dos costos adicionales en este modelo; los costos por escasez,. (C3), y los costos de ordenes retrasadas (C4).

Porque los reemplazos son instantáneos, los artículos de ordenes retrasadas son enviados al momento de ser sustituidos y los mismos no se mantienen en el inventario. Las ordenes retrasadas son consideradas como inventarios negativos; por lo tanto el inventario mínimo es un número negativo y la diferencia entre el inventario mínimo y máximo es el tamaño del lote.

 
Ordenes
  
Almacenamiento
 
Escasez + Ordenes Retrasadas
Costo Total =
xC1/Q
 +
(Q-S)2C2/(2Q)
 +
xSC3/Q + S2C4/(2Q)

Si x C3 2 < 2C1C2, entonces

Q* = M/(C2C4), y S* = M/(C2C4 +C42) - (xC3)/(C2 + C4), donde,
M = {xC2C4[2C1(C2 + C4) - C32]}1/2

De otra manera,

Q* = (2xC1/C2)1/2, con S* = 0.

Sin embargo, si el costo por escasez es C3 = 0, los valores de decisión óptima anterior se reducirán a:

Q* = [2xC1(C2 + C4)/(C2C4)]1/2, y , S* = [2xC1C2/(C2C4 + C42)]1/2

Ejemplo Numérico 2: Dado C3 = 0, y C4 = 2 C2, ¿escogería este modelo? Porque S* = Q*/3 bajo esta condición, la respuesta es, un sorprendente "Sí". Un tercio de las ordenes totales deben ser re-ordenadas.

Ejemplo Numérico 3: Considere el ejemplo numérico no. 1 con costos de escasez de C4 = $2,40 por unidad por año.

La decisión óptima es ordenar Q* = 122 unidades, permitiendo un nivel de escasez S de 81,5 unidades.

Modelo de Producción y Consumo: El modelo con reemplazos infinitos es ilustrado en la figura siguiente:

En vez de que el lote llegue instantáneamente, el mismo es asumido a llegar a una tasa de producción constante K. Esta situación se presenta cuando un proceso de producción alimenta el inventario a una tasa k mayor a la tasa de demanda x.

El nivel máximo de inventario nunca alcanza el nivel Q porque los materiales son sustraídos al mismo tiempo que el producto es elaborado. La producción toma lugar al comienzo del período. Al final del período de producción, el inventario es disminuido a una tasa de demanda x, hasta que alcanza 0 al final del ciclo.

 
Ordenes
  
Almacenamiento Holding
Costo Total =
xC1/Q
 +
(K-x)QC2/(2K)

Corrida Run Optima de Tamaño Q* = {(2C1xK)/[C2(K - x)] }1/2
Amplitud de la Corrida Run = Q*/K
Reducción de Amplitud = Q*(K-x)/(xK)
Ciclo Optimo T* = {(2C1)/[C2x(1 - x/K)] }1/2

Ejemplo Numérico 3: Suponga que la demanda para un cierto aparato de ahorro de energía es x = 1800 unidades por año (o 6 unidades por día, asumiendo 300 días hábiles por año). La compañía puede producir a una tasa anual K de 7200 unidades (o 24 por día). El costo de elaboración es C1 = $300. Existe un costo de manutención de inventarios holding de C2 = $36 por unidad por año. El problema es encontrar el tamaño óptimo de la corrida, Q.

Q* = 200 unidades por corrida de producción. El ciclo de producción óptima es 200/7200 = 0,0278 años, que es decir 8 y 1/3 al día. El número de ciclos por año es 1800/200 = 9 ciclos.


Producción y Consumo con Escasez: Suponga que la escasez esta permitida a un costo de orden retrasada re-orden C4 por unidad por período de tiempo. El ciclo lucirá como la figura siguiente:

Si se permite escasez, el punto máximo del mismo ocurre cuando la producción se inicia al comienzo del ciclo. Puede ser demostrado que:

La Producción Optima = q* = {[(2C1x)/C2][K/(K- x)][(C2+C4)/C4]}1/2

Los Períodos por Ciclo son: T = q/x

El Inventario Optimo es: Q* = t2(K-x)

La Escasez Optima es: P* = t1(K-x);

El Costo Total es: TC = {[(C2t22 + C4t12)(K-x)] + [(2C1x)/K] }/ {2(t1+t2)},

donde,

t1 = {[2xC1C2]/[C4K(K-x)(C2+C4)]}1/2,

y

t2 = {[2xC1C4]/[C2K(K-x)(C2+C4)]}1/2


A usted podría gustarle utilizar el JavaScript de Modelos de Control de Inventarios para comprobar sus cálculos. Usted podría realizar también análisis de sensibilidad mediante algunas experimentaciones numéricas para una comprensión mas profunda de los conceptos de implicaciones gerenciales lidiando con la incertidumbre de los parámetros de cada modelo.

Control de Inventarios con Demanda Incierta

Suponga que usted esta vendiendo artículos perecederos (flores), con una demanda aleatoria X. Su decisión bajo incertidumbre básicamente sigue esta pregunta: ¿Cuánto se debería ordenar de manera de maximizar mi ganancia?

Su ganancia es:

donde D es la orden diaria, P e la unidad de beneficio, y L es la perdida por realizada sobre los artículos.

Puede ser mostrado que la cantidad óptima ordenada D* con el beneficio diario máximo esperado es una función de la Función de Distribución Empírica Acumulativa (FDEA) = F(x). Mas específicamente, la cantidad óptima es X* donde F(x) es mayor o igual que el ratio P/(P + L) para la primera vez.

El siguiente ejemplo numérico ilustra el proceso. Dado P = $20, L = $10, suponga que usted ha estado tomando registros de la frecuencia de demanda pasadas D durante un período de tiempo determinado. Basado en esta información, se puede construir la tabla siguiente.

Ordenes de Cantidades Optimas
Demanda
Diaria (x) 		Frecuencia
Relativa 		FDEA Ganancia
Esperada
0 0,0067 0,0067 0,000
1 0,0337 0,0404 19,800
2 0,0842 0,1246 38,59
3 0,1404 0,2650 54,85
4 0,1755 0,4405 66,90
5 0,1755 0,6160 73,37
6 0,1462 0,7622 75,20
7 0,1044 0,8666 72,34
8 0,0653 0,9319 66,34
9 0,0363 0,9682 58,38
10 0,0181 0,9863 49,34
11 0,0082 0,9945 39,75
12 0,0034 0,9979 19,91
13 0,0013 0,9992 19,98
14 0,0005 0,9997 10,00
15 0,0002 1 -29,99

El ratio crítico P/(P + L) = 20/30 = 0,6667, indicando que D* = X* = 6 unidades.

Para verificar esta decisión, se puede utilizar la formula recursiva siguiente para calcular:

Ganancia Esperada [D+1] = Ganancia Esperada [D] - (P + L)F(x) + P

La ganancia diaria esperada utilizando esta formula es la última columna de la tabla anterior con una ganancia diaria óptima de $75,20.

A usted podría gustarle utilizar el JavaScript de Análisis de Inventarios de Períodos Simples para comprobar sus cálculos.

Modelos de Campañas Publicitarias

Introducción: Una amplia clasificación matemática de modelos publicitarios resulta en los modelos basados en el concepto de ventas, con algunas asunciones con respecto a la relación de respuesta de la función publicidad/ ventas basados en técnicas de mercadeo utilizando la teoría del comportamiento de compra de los consumidores.

Modelos de Ventas: Ventas basadas en las necesidades delos vendedores. Los modelos de venta conciernen a las necesidades de los vendedores para convertir los productos en dinero en efectivo. Uno de los modelos de venta mejor conocido es el modelo de respuesta de publicidad/ ventas (RPV) el cual asume la forma de la relación entre las ventas y la publicidad.

El Modelo de Vidale y Wolfe: Vidale y Wolfe desarrollaron un modelo de una ecuación simple de las ventas como respuesta de la publicidad, basado en estudios experimentales que miden la efectividad de la publicidad en las ventas finales. Este comportamiento a través de un periodo relativo de tiempo, a diferentes niveles de gasto en publicidad por parte de una compañía en particular, es consistente con sus observaciones empíricas, las cuales han sido desarrolladas.

Los tres parámetros en este modelo son:

Los supuestos esenciales en este modelo son como sigue a continuación:

  1. Las ventas decrecerían con ausencia de publicidad;

  2. Las ventas no incrementarán mas allá de la existencia de un nivel de saturación;

  3. La relación de dólar gastado en publicidad como respuesta en las ventas presenta una tasa constante;

  4. La publicidad se asume como operativa solo en los consumidores potenciales que no son clientes al tiempo cero; es decir, la publicidad tiene efecto en nuevos consumidores y no hace que los compradores actuales del producto incrementen el volumen de sus compras;

  5. La efectividad de un medio publicitario con respecto a otro es insignificante;

  6. Basándose en evidencia empírica, se asume que el fenómeno de las ventas puede ser representado matemáticamente por la relación:

    dS/dt = r A(t)[(m-S)/m - l S(t)

    donde dS/dt es el cambio instantáneo en la tasa de ventas al tiempo t, S es la tasa de ventas al tiempo t, A(t) es la tasa de publicidad al tiempo t, r es la respuesta constante de las ventas, l es el decrecimiento de las ventas y m es el nivel de saturación de las ventas.

Esta ecuación sugiere que el cambio o el incremento en el margen de ventas sea mayor a medida que las respuestas de las ventas sean constantemente mayores, que la caída de las ventas sea constante l, cuanto mayor sea el nivel de saturación, y mayor sea el gasto en publicidad.

Los tres parámetros r, l, y m son constantes para un producto y campaña publicitaria determinada.

La respuesta de las ventas, r, es valorado y mesurado mediante la medición de la tasa de ventas resultante de un monto de publicidad dado en un área de prueba con condiciones controladas. El decaimiento constante de las ventas l, es valorado mediante la medición del decrecimiento de las mismas en el área de prueba cuando la publicidad se reduce a cero. El nivel de saturación de las ventas, m, es valorado mediante la información de investigaciones del mercado en su totalidad. Note que el término (m-S)/S es el restante de las ventas potenciales que pueden ser alcanzadas mediante las campañas publicitarias.

El modelo puede ser arreglado y escrito como:

dS/dt + [r A(t)/m + l)] S(t) = r A(t)

El siguiente representa una respuesta típica de ventas a una campaña publicitaria.

La campaña publicitaria tiene una tasa constante de gastos en publicidad A(t) =A que se mantiene por un período de duración T, después del cual A es casi cero:

             æ A          for 0 £ t £ T,
A(t) =   ç
            è 0          for t >T

A pesar de que muchos investigadores de mercadeo tienen alineado el acercamiento de ASR como una escuela establecida de modelos de publicidad, ellos aceptan abiertamente que el problema mas agraviado es la suposición de la forma de la función ASR. Adicionalmente, los modelos ASR no consideran las necesidades y motivos que dominan el comportamiento de los consumidores. Es bien sabido que los gerentes de mercadeo están preocupados en proporcionar el beneficio de los productos, los cambios en la acttud de las marcas y productos, e influenciar la percepción de los consumidores. Los gerentes de mercadeo saben que la planificación publicitaria debe estar fundamentada en fuerzas sicológicas y sociales que condicionan el comportamiento de los consumidores, es decir, conocer que mensaje va hacia el interior de las mentes de los consumidores.

Modelos de Compra o Adquisición: Las compañías de negocios modernos han orientado sus campañas publicitarias hacia una aproximación absoluta del comportamiento de compra de los consumidores mas que a las ventas. Este acercamiento se fundamenta en la sabiduría del mercadeo: los profesionales de mercadeo deben saber lo que los consumidores potenciales desean y/ o quieren oír con el objetivo de vender algo. Ha sido considerablemente discutido con anterioridad considerable en la literatura de mercadeo sobre "el comportamiento del consumidor," esta discusión se centra en torno a la necesidad del mercadeo de estar orientada al consumidor, de manera de estar preocupada con la idea de satisfacer las necesidades de los consumidores por medio de productos y el conjunto entero de factores asociados con la creación, entrega, y consumo final del mismo. Esto es posible ahora mediante la consideración de la necesidad de avances tecnológicos en el área de mercadeo tales como las "tormentas cerebrales."

El acercamiento de los modelos de publicidad a los patrones de comportamiento de compra de los consumidores presumen que la publicidad influye en las ventas mediante el anuncio de sabores, preferencias y actitud de los consumidores, y los esfuerzos de las firmas por comunicar estos resultados en una compra.

Debido a que existen innumerables factores socio-sicológicos que afectan los comportamientos de consumo, algunos complejos y desconocidos por los publicistas, es preferible considerar la versión probabilística del modelo de comportamiento de compras de los consumidores. Debido al efecto disminuido de la publicidad, por lo general los publicistas pulsan la publicidad como oposición a que la publicidad constante podría incrementar la efectividad de la publicidad, especialmente sobre el impacto de repetición de la publicidad.

El modelo operacional con características adicionales es normalmente derivado por una estrategia de publicidad óptima sobre la duración finita de una campaña publicitaria. Las estrategias prescritas son maximizadoras de la función de utilidad descontada la cual incluye la actitud de la firma hacia la incertidumbre de las ventas. Los asuntos operacionales necesarios tales como los parámetros de estimación y de auto-validación también son recomendados.

La literatura de mercadeo proporciona fuerte evidencia de que los consumidores sustituyen reglas para obtener información acerca de la calidad de productos, valor percibido, y precios. El menor costo búsqueda de asociado a las reglas, por ejemplo, podría ser mayor que la compensación monetaria o la perdida de calidad. Generalmente, los consumidores tienden a percibir los productos con gran publicidad como los de mejor calidad. Estudios sicológicos han descubierto que el comportamiento humano es una "manera de actitud" y evalúa casi todo lo que entra en contacto con la "revisión de los valores." Considere la pregunta "¿Qué piensa acerca esta marca en particular?", De seguro, la respuesta dependerá del grado que usted le guste o disguste, aprecie o desprecie la marca. Por lo tanto el meollo del modelo de comportamiento del consumidor Quid es que los especialistas en mercadeo intentan reconocer a los consumidores como una forma de actitud, los cuales constantemente revisan todos los valores, así sea dentro de segmentos dados. Una vez el comportamiento hacia la dirección del objetivo es manifestado, el consumidor experimenta las consecuencias de su comportamiento. El o ella utiliza esta experiencia como fuente de aprendizaje en el cual revisará su actitud hacia este producto o servicio determinado. Muchos investigadores han expresado el hecho de que solo la actitud determina los comportamientos subsecuentes.

El organigrama de un modelo simple es mostrado a continuación:

La estructura del proceso de decisiones de un consumidor típico en referencia a una marca X específica, contiene tres valores funcionales que llamamos actitud A(t), nivel de compra B(t) y comunicación C(t).

Modelo de Nicosia: El estado de las ecuaciones dinámicas del modelo de Nicosia están descritas por las dos ecuaciones diferenciales/ algebraicas lineales siguientes:

B¢(t) = dB(t)/dt = b[A(t) - bB(t)]

A¢(t) = dA(t)/dt = a[B(t) - aA(t)] + C(t)

Donde:

B(t) = Comportamiento de compra (o consumo); es decir tasa de compra al tiempo t.

A(t) = Actitud del consumidor hacia la marca, la cual resulta de una variedad compleja de iteraciones de varios factores, alguno de los cuales están indicados en la figura anterior.

C(t) = El impacto de la comunicación (la campaña publicitaria) hecha por la firma. Este podría ser simplemente un estimulo, un nuevo diseño en la presentación (paquete) o una simple publicidad de alguna marca en particular. Una estrategia de mercadeo es exitosa cuando se desarrolla un producto y los estímulos de promoción que los consumidores perciben como relevante para sus necesidades. Las necesidades de los consumidores también están influenciadas por factores tales como previas experiencias, e influencias sociales. Dada la disminución del efecto de la publicidad, consideramos C(t) como la función de pulso, como opuesta a la función de publicidad constante.

a, b, a, y b son los parámetros de "personalidad" de las ecuaciones del modelo. Estos parámetros son asumidos constantes con respecto al tiempo.

Los principales inconvenientes del modelo descriptivo anterior son:

1) La tasa de publicidad es constante a través del tiempo. Esta claro que los retornos bajo un modelo de publicidad constante disminuyen a través del tiempo, lo que implica que no están relacionados al volumen de las ventas; por lo tanto cualquier gasto adicional en publicidad no traerá ningún incremento sustancial en los ingresos por venta. El término "modelos de publicidad" ha sido utilizado para describir el proceso de mejorar las ventas de un producto o servicio. Un gasto sustancial en marketing es un gasto en publicidad. El efecto de repetición de un estímulo en la habilidad de los consumidores de recordar el mensaje es el asunto mas importante en la teoría de aprendizaje. Por supuesto, esta bien establecido que la publicidad debe ser continua para evitar que sea olvidada.

Política de Publicidad de Pulsaciones: : La política de publicidad por pulsaciones (PPP) es una política de alta intensidad constante de publicidad, alternada con períodos de no-publicidad, como se muestra en la figura siguiente:

El PPP podría preferirse a una publicidad constante durante la duración de la campaña.

2) La publicidad tiene un horizonte infinito de tiempo. Este horizonte infinito decrece el uso del modelo debido a que el presupuesto de planificación para los gastos en publicidad raramente tienen horizontes infinitos. Sin embargo, en el modelo de Nicosia no se identifica claramente la función de respuesta de las ventas cuando la publicidad es discontinua.

Conclusiones y Recomendaciones: Los modelos mas realistas deben considerar el problema de designación de una publicidad óptima (digamos, una política de pulsaciones) para una campaña publicitaria de tiempo finito. Desde que existen múltiples factores socio-sicológicos afectando las compras, muchos de ellos complejos y desconocidos por el publicista, el modelo debe ser construido en un ambiente probabilístico. También deben ser aplicados los procesos estadísticos para la estimación de los parámetros de mercado. La estrategia preescrita podría ser la maximización de la función de utilidad descontada. Reconociendo que los gerentes de mercadeo están preocupados por las implicaciones económicas y de riesgo de sus alternativas de decisión, la función de utilidad debería incluir la actitud de los tomadores de decisiones hacia el riesgo percibido.

La Cadena de Markov

Muchas de las más poderosas técnicas analíticas aplicadas en negocios, están basadas en la teoría de la cadena de Markov. La cadena de Markov es un caso especial del proceso de Markov, el cual en si mismo es un caso especial del proceso aleatorio o estocástico.

En términos mas generales, un proceso aleatorio es una familia, o grupo ordenado de variables relacionadas X(t) donde t es un parámetro de indexación, usualmente tiempo cuando se habla de realizar evaluaciones.

Existen diferentes tipos de procesos aleatorios. Dos de las características más distinguidas de los procesos son: (1) su estado espacial o el conjunto de valores del proceso que las variables aleatorias pueden tener, y (2) la naturaleza de los parámetros de indexación. Podemos clasificar procesos aleatorios en cada una de estas dimensiones.

  1. Estado Espacial:
    • estado- continuo: X(t) puede tomar cualquier valor sobre el intervalo continuo o conjunto de dichos intervalos
    • estado- discreto: X(t) tiene solo valores posibles contables o finitos. {x0, x1 … ,xi,..}


      Un proceso aleatorio de estado- discreto es llamado comúnmente una cadena.

  2. Parámetro de Indexación (normalmente es el tiempo t):
    • tiempo- discreto: los tiempos permitidos a los cuales los cambios en valores que puedan ocurrir son finitos o contables X(t) que pueden ser representados como conjunto {X i}
    • estado- continuo: los cambios pueden ocurrir en cualquier lugar dentro del intervalo finito o del conjunto de dichos intervalos

Cambios en los Estados del Sistema
Continuas Discretas
Tiempo Continuo Nivel de agua
contenido en una represa 		Número de
clientes en un banco
Discreto Rango de temperaturas
diarias 		Ventas al
final del día
Una Clasificación de Procesos Estocásticos

El estado de un proceso aleatorio de tiempo-continuo al tiempo t tiene un valor de X(t); el estado de un proceso de tiempo-discreto al tiempo n es el valor de X p. Una cadena de Markov es un proceso aleatorio de estado-discreto que comienza en el tiempo t (cadena de tiempo- continuo) o n (cadena de tiempo- discreto) que solo depende del estado actual X(t) o Xp, y ni de cómo la cadena alcanzo su estado corriente o de cuanto tiempo ha permanecido en ese estado. Consideramos una cadena de Markov de estado-finito de tiempo {Xt, t= 0, 1, 2, } con probabilidades de transición estacionarias (condicionales):

P [Xt+1 = j | Xt = i ]

donde i, y j pertenecen al conjunto S.

Supongamos que P = pij denota la matriz de probabilidades de transición. Las probabilidades de transición entre t y t + 1 son indicadas por pn ij y por la matriz de transición Pn = Pn

Una Cadena Típica de Markov con tres Estados y
Sus Probabilidades Tradicionales Estimadas

Elementos de una Cadena de Markov: Una cadena de Markov consiste de

Representación Esquemática Pasajera, Estados Cerrados y Absorbidos

En la figura anterior, el estado A es un estado absorbente. Una vez que el proceso entra en este estado, no lo abandona. Similarmente, los estados Dl, D2, y D3 representan un conjunto cerrado. Después de haber introducido D1, el proceso se puede mover a D2 o D3, pero no puede hacer otra transición a ningún otro estado. En contraste, los estados Bl, B2 y B3 representan un conjunto pasajero, conectando el estado absorbente A con el conjunto cerrado D.

Dos Cadenas de Markov Especiales:

El Resultado Principal: Si el límite de pn ij = pj existe con n aproximaciones, la distribución limitante o estacionaria de la cadena P = {pj puede ser encontrada mediante la resolución del siguiente sistema de ecuaciones lineales: P P = P

Ejemplo Numérico: La siguiente matriz representa una cadena de Markov de cuatro estados con la matriz de probabilidad pasajera:

P= |0,25 0,20 0,25 0,30|
|0,20 0,30 0,25 0,30|
|0,25 0,20 0,40 0,10|
|0,30 0,30 0,10 0,30|

Note que la suma de cada columna en esta matriz es uno. Cualquier matriz con estas propiedades es llamada matriz de probabilidad o matriz de Markov. Estamos interesados en la pregunta siguiente:

¿Cuál es la probabilidad de que el sistema este en el iésimo estado, al n-ésimo período de transición?

Para responder esta pregunta, primero definimos el vector estado. Para una cadena de Markov, la cual tiene k estados, el vector estado para un periodo de observación n, es el vector columna definido por



x(n) = x1
x2
.
.
xk


donde xi = probabilidad de que el sistema es en el iésimo estado al momento de la observación. Note que la suma de las entradas del vector estado tiene que ser uno. Cualquier vector columna x,

x = x1
x2
.
.
xk

donde x1+ x2+ …. +xk = 1

[x1,x2,…. ,xk] es llamado un vector probabilidad.

Considere nuestro ejemplo - suponga que el vector de estado inicial x0 es:

x(0) = 1
0
0
0

En el próximo periodo de observación digamos, al final de la primera semana, el vector estado será
x(1)= Px(0) = 0,25
0,20
0,25
0,30

Al final de la 2da semana el vector estado es Px1


x(2) = Px(1) = |0,25 0,20 0,25 0,30| |0,25| = |0,2550 |
|0,20 0,30 0,25 0,30| |0,20| = |0,2625 |
|0,25 0,20 0,40 0,10| |0,25| = |0,2325 |
|0,30 0,30 0,10 0,30| |0,30| = |0,2500 |


Note que podemos calcular x2 directamente utilizando x0 como

x(2) = Px(1) = P(Px(0)) = P2 x(0)

Similarmente, podemos encontrar el vector estado para 5to, 10mo, 20avo, 30avo, y 50avo períodos de observación.

x(5)= P5x(0) = 0,2495
0,2634
0,2339
0,2532

x(10)= P10x(0) = 0,2495
0,2634
0,2339
0,2532

x(20)= P20x(0) = 0,2495
.2634
0,2339
0,2532

x(30) = 0,2495
0,2634
0,2339
0,2532

x(50) = 0,2495
0,2634
0,2339
0,2532



Los mismos resultados limitantes pueden ser obtenidos resolviendo el sistema de ecuaciones lineales P P = P utilizando este JavaScript, el cual sugiere que el vector estado se aproxima a algunos vectores fijos, mientras el número de períodos observaciones incrementa. Este no es el caso para cada cadena de Markov. Por ejemplo, si

P = 0 1
1 0

, y

x(0) = 1
0

Podemos calcular el vector estado para diferentes períodos de observacion:
x(1) = |0| , x(2) =
|1|
 , x(3) =
|0|
 , x(4) =
|1|
 ,......., x(2n) =
|1|
 , y x(2n+1) = |0|
|1|
|0|
|1|
|0|
|0|
 |1|

Estos cálculos indican que el sistema oscila y que no se aproxima a ningún a ningún vector fijo.

A usted podría gustarle utilizar el JavaScript de Multiplicación de Matrices y Calculador-I de la Cadenas de Markov para comprobar sus cálculos y realizar algunas experimentaciones numéricas para una comprensión mas profunda de estos conceptos.

Modelo de Insumo- Producto de Leontief

Modelo de Insumo- Producto de Leontief: Este modelo considera una economía con un numero limitado de industrias. Cada una de estas industrias utiliza insumos propios y de otras industrias para producir un producto.

En el Modelo de Insumo- Producto de Leontief, el sistema económico es asumido de tener n industrias con dos tipos de demanda en cada industria: demanda externa (desde afuera del sistema) y demanda interna (demanda ubicada en una industria por otra en el mismo sistema.) Asumimos que no existe sobre producción, por lo tanto la suma de la demanda interna y externa es igual a la demanda total para cada industria. Dejemos que xi denote la producción de la iésima industria, e i la demanda externa en la iésima industria, y aij es la demanda interna ubicada en la iésima industria por la jésima industria. Esto significa que la entrada aij en la matriz tecnológica A = [aij] es el número de unidades de producto de la industria i necesarios para producir 1 unidad de producción de la industria j. El monto total que la industria j necesita de la industria i es aijxj. Bajo la condición de que la demanda es igual al ,producto de cada industria, tendremos un sistema lineal de ecuaciones para resolverlo.

Ejemplo Numérico: Un sistema económico esta compuesto por tres industrias A, B, y C. Ellas están relacionadas como sigue:

Industria A requiere lo siguiente para producir $1 de su producto:

$0,10 de su propio producto;
$0,15 de los productos de la industria B; y
$0,23 de los productos de la industria C.

Industria B requiere lo siguiente para producir $1 de su producto:

$0,43 de los productos de la industria A; y
$0,03 de los productos de la industria C.

Industria C requiere lo siguiente para producir $1 de su producto:

$0,02 de su propio producto.
$0,37 de los productos de la industria B; y

Las ventas a grupos no productores (demanda externa) son:


$20 000 para la industria A, $30 000 para la industria B, $25 000 para la industria C

Que nivel de producción para estas tres industrias logra el balance de la economía?

Solución: Escriba la ecuación que muestra el balance entre producción y consumo por cada industria X = DX + E:

Producción
                  Consumo
  
para
  
para A
para B
para C
externas
Industria A:
x1
=
0,10x1
+
0,43x2
+
20 000
Industria B:
x2
=
0,15x1
+
0,37x3
+
30 000
Industria C:
x3
=
0,23x1
+
0,03x2
+
0,02x3
+
25 000

Ahora resuelva este sistema de ecuaciones resultantes para los niveles de producción Xi, i = 1, 2, 3.

A usted podría gustarle utilizar el JavaScript de Resolver Sistemas de Ecuaciones Aplicadas a la Inversión de Matrices para comprobar sus cálculos y realizar algunas experimentaciones numéricas para una compresión mas profundo de estos conceptos.

Declaración de derechos de propiedad intelectual: El uso legítimo, según las pautas de 1994 guías de consulta justas del uso para los multimedia educativos, de los materiales presentados en este sitio Web está permitido para propósitos educativos no comerciales.
Este sitio puede duplicarse, intacto con esta declaración, en cualquier servidor de acceso público y puede vincularse a cualquier otra página Web. Todos los archivos se encuentran disponibles en http://home.ubalt.edu/ntsbarsh/Business-stat para el duplicado.

Agradecería recibir comentarios, sugerencias e inquietudes por e-mail. Gracias.

Profesor Hossein Arsham   

Vuelta a:

Ciencia de la Administración Aplicada para Gerentes y Lideres Gerenciales

Modelos Deterministas: Optimización lineal

Optimización de Enteros y Modelos de Redes

Introducción a la Teoría de Juegos

Modelos Probabilísticos: Del análisis de la decisión

Toma de Decisiones con Periodos de Tiempo Crítico en Economía y Finanzas

Razonamiento Estadístico para la Toma de Decisiones Gerenciales

Una Clasificación de JavaScript Estadíticos

El Aprendizaje con la Asistencia del Computador

Temas en Algebra Lineal

Construcción de Regiones de Sensibilidad General de Programación Lineal

EOF: Ó 1994-2015.