Polynomial regression models are often used in economics areas such as utility function , forecasting, cost-befit analysis, etc. This JavaScript provides polynomial regression up to fourth degrees. This site also presents a JavaScript implementation of the Newton's root finding method.
Prior to using this JavaScript it is necessary to construct the scatter-diagram for your data. Visual inspection of the scatter-diagram enables us to determine what degree of polynomial regression is the most appropriate for fitting to your data.
Enter your at-least-8, and up-to-16 sample (X, Y) and the data sets of X2, and X3, for third-order polynomial, for the fouth order enter also X4. After entering your necessary entries, then click the Calculate button.
Obviously, sample size is going to limit how many terms you want to use in the polynomial regressions.
Notice: The JavaScript enables you to perform serial-residual analysis provided you enter the independent variable X in increasing order.
In entering your data to move from cell to cell in the data-matrix use the Tab key not arrow or enter keys.
The Newton's Root-Finder: Newton devised an iterative process, called Newton's Method for finding the roots of functions.
A root of a function f(X) is a number X* for which f(X*) = 0. That is, the graph of y = f(X) crosses the X-axis at X*.
Here are the steps for the Newton's root-finder method:
- Guess a number X0 If f(X0) = 0, we are done. If not,
- Draw the vertical line from (X0,0) to (X0, f(X0)).
- Draw the line tangent to the graph of y = f(X) at the point (X0, f(X0)).
- Usually, this tangent line intersects the X-axis at a point (X1, 0).
- Repeat the process with X1 taking the place of X0.
- Continue until f(Xn) is close enough to 0.
This process is illustrated for a typical example in the following figure:
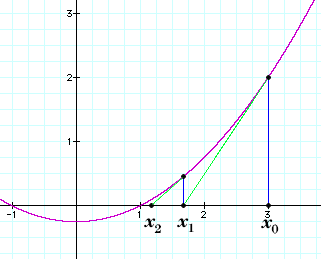
A Geometrical Interpretation of the First Few of Iterations of Newton's Formula
Click on the image to enlarge it
In other words, the Newton iteration is then given by the following procedure: start with an initial guess of the root X0, then find the limit of of the following Newton’s recurrence formula:
|
Numerical Example: Suppose we are intersted in finding a root of equation X3 - 2X2 + 3X - 43 = 0. The following The Newton's Root-Finder JavaScript is an implementation of Newton’s recurrence formula.
Exercise your Skill: Consider the following 4th order polynomial f(X) = X4 + 48X3 + 18X2 - 4X, which has four roots all within the range [-2.0, 2.0], can you find them all? Try it by utilizing the JavaScript.